在 PHP 中，有多种方法可以用来输出内容。下面是其中的几种：

1、echo：

这是最常见的输出语句之一，可以输出一个或多个字符串。它是一个语言结构，可以省略括号。使用示例如下：

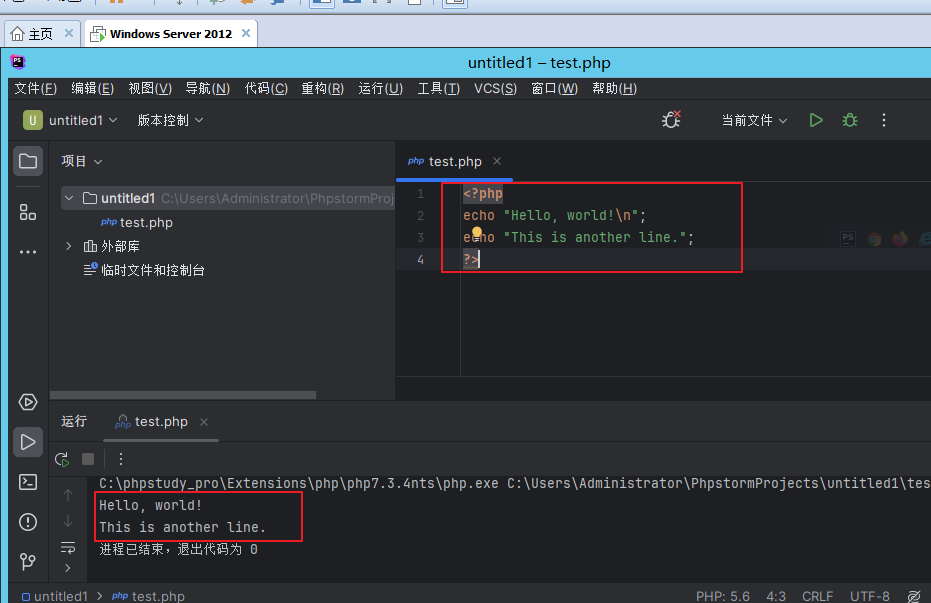
<?php
// 使用 echo 语句输出一个字符串
echo "Hello, world!\n";

// 可以使用多个 echo 语句输出多行内容
echo "This is another line.";
?>

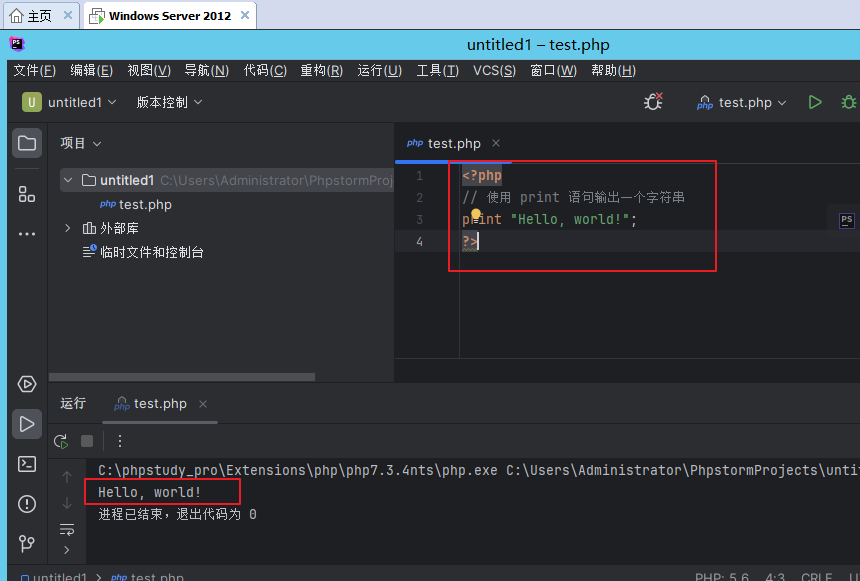
2、print：

print 语句也可以输出一个字符串，但只能输出一个字符串，并且始终返回值为 1。使用示例如下：

<?php
// 使用 print 语句输出一个字符串
print "Hello, world!";
?>

3、var_dump：

这个函数可以用来输出一个或多个变量的详细信息，包括数据类型、长度和值等。使用示例如下：

<?php
$x = 123;
$y = "hello";

// 使用 var_dump 函数输