LCR 090. 打家劫舍 II(leetcode)动态规划

news2025/11/1 2:14:57

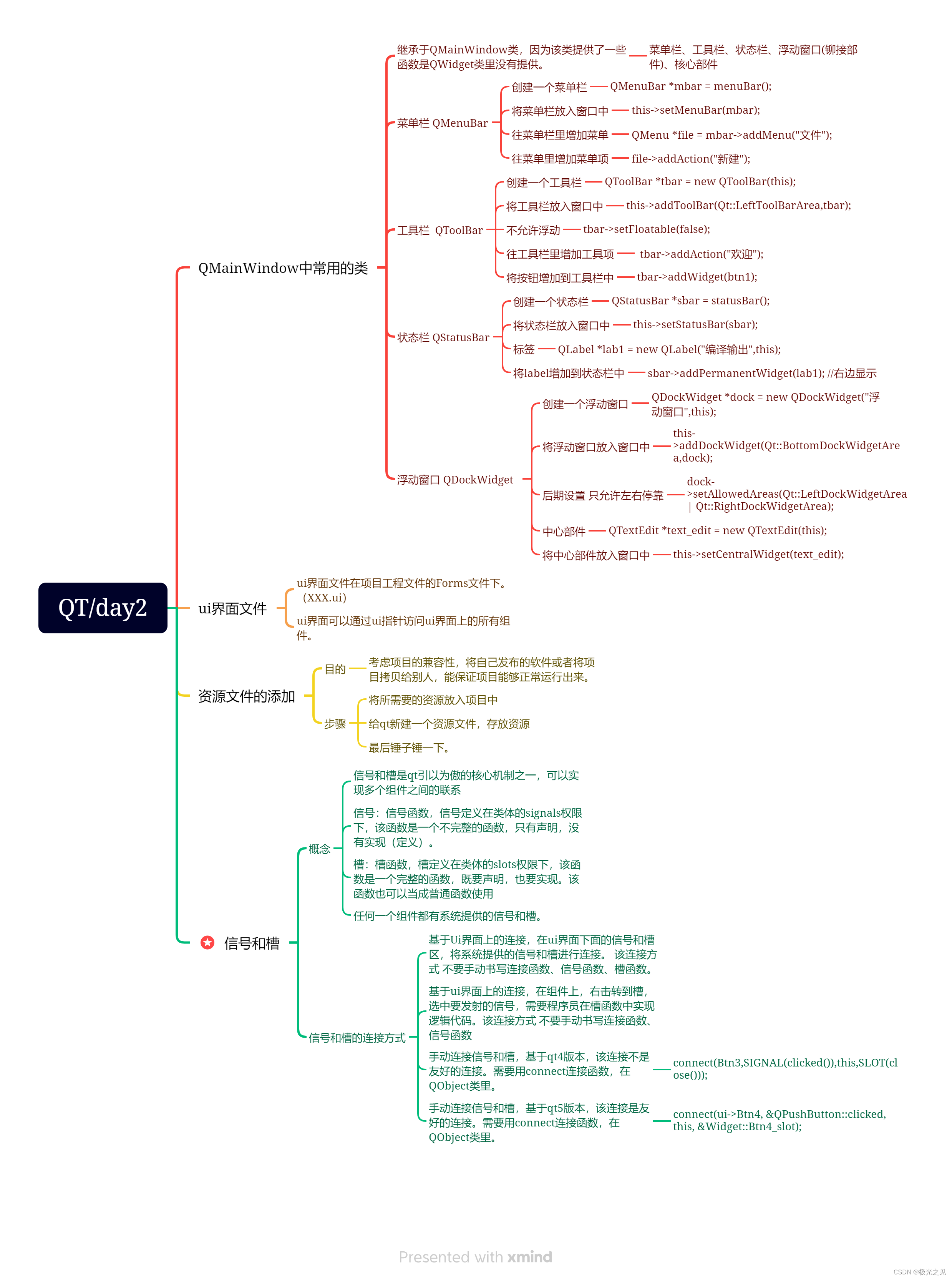
文章目录

前言
一、题目分析
二、算法原理
- 1.状态表示
- 2.状态转移方程
- 3.初始化
- 4.填表顺序
- 5.返回值是什么
三、代码实现
总结

前言

在本文章中，我们将要详细介绍一下LeetcodeLCR 090. 打家劫舍 II。采用动态规划解决，这是一道经典的多状态dp问题

一、题目分析

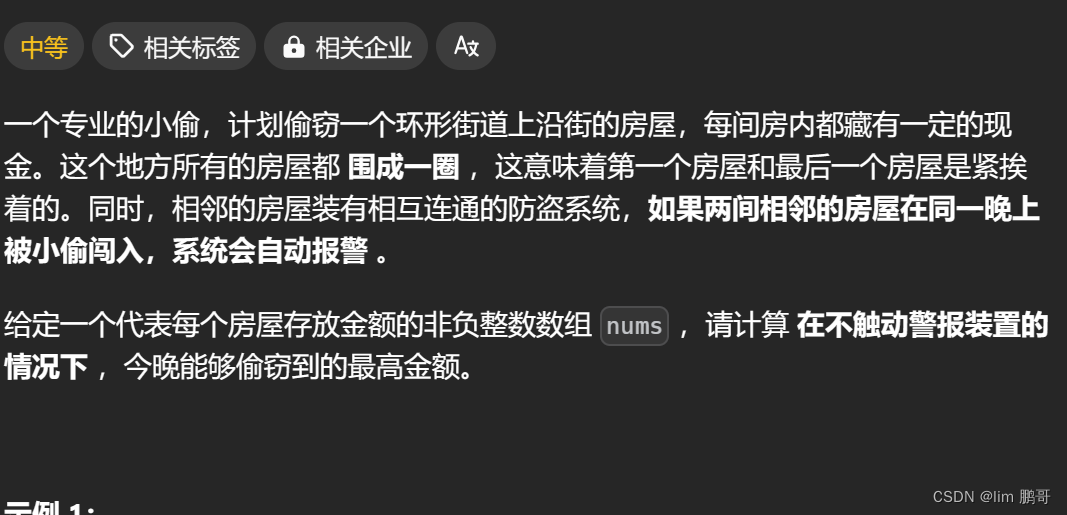
在这里插入图片描述
计算小偷能偷到的最大金额数，并且题目规定：
🥉.两个相邻的房屋不能被偷
🥉.第一个房屋和最后一个房屋不能被偷
规定1比较好解决，对于规定2，我们采用分情况讨论的方法解决
🍔.第一个房间偷，第二个房间和最后一个不被偷，在（2，n-2）下标之间寻找最大金额，再加上nums[0].
🍔.第一个房间不被偷，最后一个房间不确定，在（1，n-1）下标之间寻找最大金额
🍔.二者取最大值，就是题目所返回的值

二、算法原理

1.状态表示

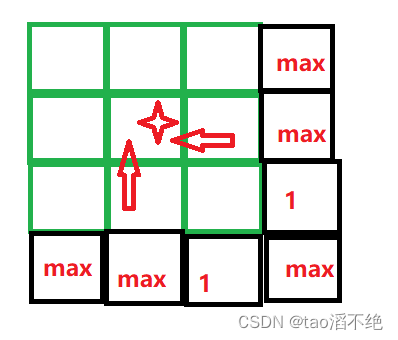
列出dp表，dp表中值的含义是什么
这可以细分为两个表，因为经过该房间时不确定偷与不偷
⭐️ .f[i]表示到达i房间时，资金被偷
⭐️.g[i]表示到达i房间时，资金没有被偷

2.状态转移方程

根据最近一步划分问题
🌟 f[i]:i位置被偷，那么根据题目规定，i-1位置就不能被偷，这不就正好是g[i-1],再加上i位置被偷的资金;
🌟g[i]:i位置没有被偷，i-1位置我们不确定有没有被偷，所以需要分为两种情况，这两种情况取最大值
🐧.i-1位置也没有被偷，就是g[i-1]
🐧.i-1位置被偷了，就是f[i-1]
结论：
f[i]=g[i-1]+nums[i];
g[i]=max(g[i-1],f[i-1])

3.初始化

保证填表不越界
f[1]需要g[0]的值；g[1]需要g[0]和f[0]的值, 所以需要初始化g[0]和f[0].
不用开辟额外的空间，这道题目的初始化很简单。
注意：数组的下标和边界条件

4.填表顺序

两个表一起填，从左往右

5.返回值是什么

max(f[n-1],g[n-1]);

三、代码实现

class Solution {
public:
    int massage(vector<int>& nums,int left,int right) 
    {
        if(left>right)
        {
            return 0;
        }
        //建表
        int n=nums.size();
        int f[n];
        int g[n];
        //初始化
        for(int i=0;i<n;i++)
        {
            f[i]=g[i]=0;
        }
        f[left]=nums[left];
        g[0]=0;
        //填表
        for(int i=left;i<=right;i++)
        {
            f[i]=g[i-1]+nums[i];
            g[i]=max(g[i-1],f[i-1]);
        }
        //返回值
        return max(f[right],g[right]);

    }
    int rob(vector<int>& nums) 
    {
        int  n=nums.size();
        //下标
        int ret1=massage(nums,2,n-2)+nums[0];
        int ret2=massage(nums,1,n-1);
        return max(ret1,ret2);
    }
};