文章目录
- 前言
- 回归和分类
- Logistic回归
- 线性回归
- Sigmoid函数
- 把回归变成分类
- Logistic回归算法的数学推导
- Sigmoid函数与其他激活函数的比较
- Logistic回归实例
- 1. 数据预处理
- 2. 模型定义
- 3. 训练模型
- 4. 结果可视化
- 结语
前言
当谈论当论及机器学习中的回归和分类问题时,很容易被“Logistic回归”中的“回归”一词所误导。尽管Logistic回归中有"回归"二字,但它实际上是一种用于分类问题的算法,而不是回归问题。在这篇博客中,我们将深入研究Logistic回归,讨论其背后的原理以及如何手动实现它。
回归和分类
在机器学习领域,回归(Regression) 和 分类(Classification) 是两种主要的预测问题类型。回归和分类都属于监督学习,但它们解决的问题不同。
- 回归问题: 旨在预测一个连续值,例如房屋价格、股票价格、销售额等。
- 分类问题: 关注对数据进行离散类别的预测,将数据分为不同的类别,比如预测一封电子邮件是否为垃圾邮件等。
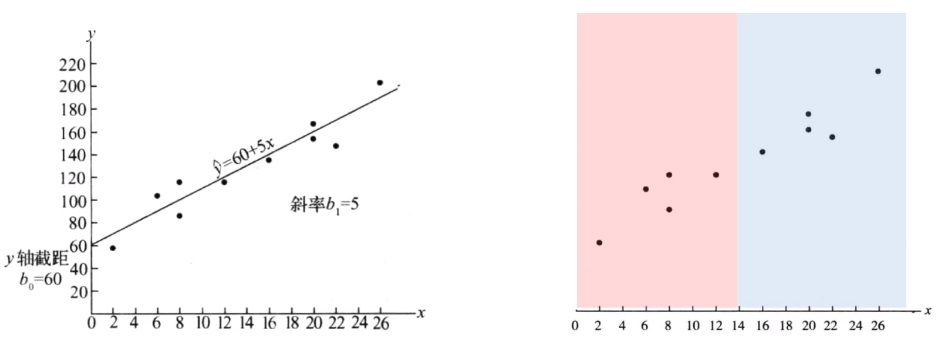
不要被Logistic回归的名字所欺骗,Logistic回归虽然带有 “回归” 二字,但实质上是一种用于二分类的算法。
Logistic回归
Logistic回归是一种基于概率的线性分类算法,尤其适用于解决二分类问题。
与线性回归不同,它通过将线性函数的输出映射到一个介于0和1之间的概率来实现分类。就这样把连续的预测值转换为概率输出的形式,这个概率可以表示为样本属于某个类别的概率。
在Logistic回归中,我们使用一个称为Sigmoid函数的特殊函数,他叫Logistic(逻辑)函数,也叫激活函数。
简单来说:Logistic回归 = 线性回归 + Sigmoid函数
线性回归
首先,让我们回顾一下线性回归。
线性回归是一种用于建模自变量(输入特征)与因变量(输出)之间线性关系的模型。
线性回归的目标是找到一条直线(或超平面),最大程度地拟合输入数据。其数学表达式为:
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β n X n + ϵ Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \ldots + \beta_nX_n + \epsilon Y=β0+β1X1+β2X2+…+βnXn+ϵ
其中, Y Y Y 是预测值, β 0 \beta_0 β0 是截距, β 1 , β 2 , … , β n \beta_1, \beta_2, \ldots, \beta_n β1,β2,…,βn 是权重, X 1 , X 2 , … , X n X_1, X_2, \ldots, X_n X1,X2,…,Xn 是特征, ϵ \epsilon ϵ 是误差。
线性模型可以表示为:
h ( x ) = θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n h(x) = \theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n h(x)=θ0+θ1x1+θ2x2+...+θnxn
其中, h ( x ) h(x) h(x) 是预测值, θ 0 , θ 1 , . . . , θ n \theta_0, \theta_1, ..., \theta_n θ0,θ1,...,θn 是模型的参数。
Sigmoid函数
为了将线性回归转变为分类问题,我们引入了Sigmoid函数。
Sigmoid函数是一种常用的激活函数,其图像呈S形状。它的特点是在输入接近正无穷或负无穷时,输出趋近于1或0,而在接近零时,输出约为0.5。
这种性质使得sigmoid函数在将线性输出映射到概率时非常有用。它的导数也相对简单,这对于梯度下降等优化算法至关重要。
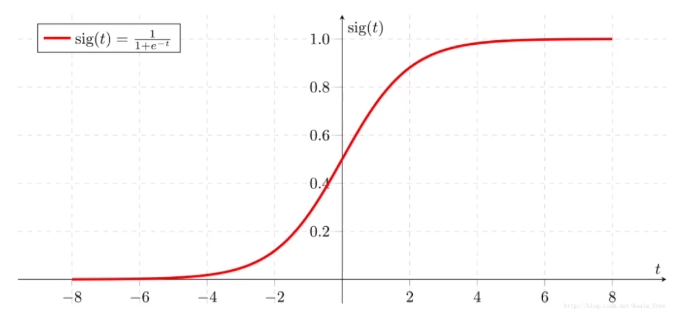
把回归变成分类
Sigmoid函数将任意实数值映射到一个范围在0和1之间的概率值。其表达式为:
σ ( z ) = 1 1 + e − z \sigma(z) = \frac{1}{1 + e^{-z}} σ(z)=1+e−z1
这里, z z z 是线性模型的输出。将Sigmoid函数应用于线性模型的输出,我们得到了Logistic回归的基本公式:
h ( x ) = σ ( θ 0 + θ 1 x 1 + θ 2 x 2 + . . . + θ n x n ) h(x) = \sigma(\theta_0 + \theta_1x_1 + \theta_2x_2 + ... + \theta_nx_n) h(x)=σ(θ0+θ1x1+θ2x2+...+θnxn)
通过这个转换,我们可以将任意实数范围内的输出映射到 [ 0 , 1 ] [0, 1] [0,1]之间。
Logistic回归算法的数学推导
现在我们已经得知Logistic回归是一种分类算法,它使用一个Sigmoid函数将输入映射到0和1之间的概率值。
假设我们有一个样本 x x x,那么它属于类别1的概率可以表示为:
P ( y = 1 ∣ x ) = 1 1 + e − ( w T x + b ) P(y=1|x) = \frac{1}{1+e^{-(w^Tx + b)}} P(y=1∣x)=1+e−(wTx+b)1
其中, w w w 是特征的权重向量, x x x 是输入特征向量, b b b是偏置项(bias)。我们可以将所有样本的预测结果表示为一个向量:
y ^ = σ ( X w + b ) \hat{y} = \sigma(Xw+b) y^=σ(Xw+b)
其中, σ ( x ) \sigma(x) σ(x)是Sigmoid函数:
σ ( x ) = 1 1 + e − x \sigma(x) = \frac{1}{1+e^{-x}} σ(x)=1+e−x1
我们的目标是最小化交叉熵损失函数:
J ( w , b ) = − 1 m ∑ i = 1 m [ y ( i ) log ( y ^ ( i ) ) + ( 1 − y ( i ) ) log ( 1 − y ^ ( i ) ) ] J(w,b) = -\frac{1}{m}\sum_{i=1}^{m}{[y^{(i)}\log(\hat{y}^{(i)})+(1-y^{(i)})\log(1-\hat{y}^{(i)})]} J(w,b)=−m1i=1∑m[y(i)log(y^(i))+(1−y(i))log(1−y^(i))]
其中, m m m是样本数量, y ( i ) y^{(i)} y(i)是第 i i i个样本的真实标签, y ^ ( i ) \hat{y}^{(i)} y^(i)是它的预测结果。我们可以使用梯度下降法来最小化损失函数。权重和偏置项的更新规则如下:
w = w − α ∂ J ( w , b ) ∂ w w = w - \alpha\frac{\partial J(w,b)}{\partial w} w=w−α∂w∂J(w,b)
b = b − α ∂ J ( w , b ) ∂ b b = b - \alpha\frac{\partial J(w,b)}{\partial b} b=b−α∂b∂J(w,b)
其中, α \alpha α是学习率。我们可以通过计算损失函数对权重和偏置项的偏导数来得到它们的梯度:
∂ J ( w , b ) ∂ w = 1 m X T ( y ^ − y ) \frac{\partial J(w,b)}{\partial w} = \frac{1}{m}X^T(\hat{y}-y) ∂w∂J(w,b)=m1XT(y^−y)
∂ J ( w , b ) ∂ b = 1 m ∑ i = 1 m ( y ^ ( i ) − y ( i ) ) \frac{\partial J(w,b)}{\partial b} = \frac{1}{m}\sum_{i=1}^{m}{(\hat{y}^{(i)}-y^{(i)})} ∂b∂J(w,b)=m1i=1∑m(y^(i)−y(i))
Sigmoid函数与其他激活函数的比较
Sigmoid函数在Logistic回归中被广泛使用,因为它能将输出转化为概率值。
除了sigmoid函数,还有其他一些常用的激活函数,比如ReLU(Rectified Linear Unit)函数。这些函数在神经网络和深度学习中扮演着重要的角色。
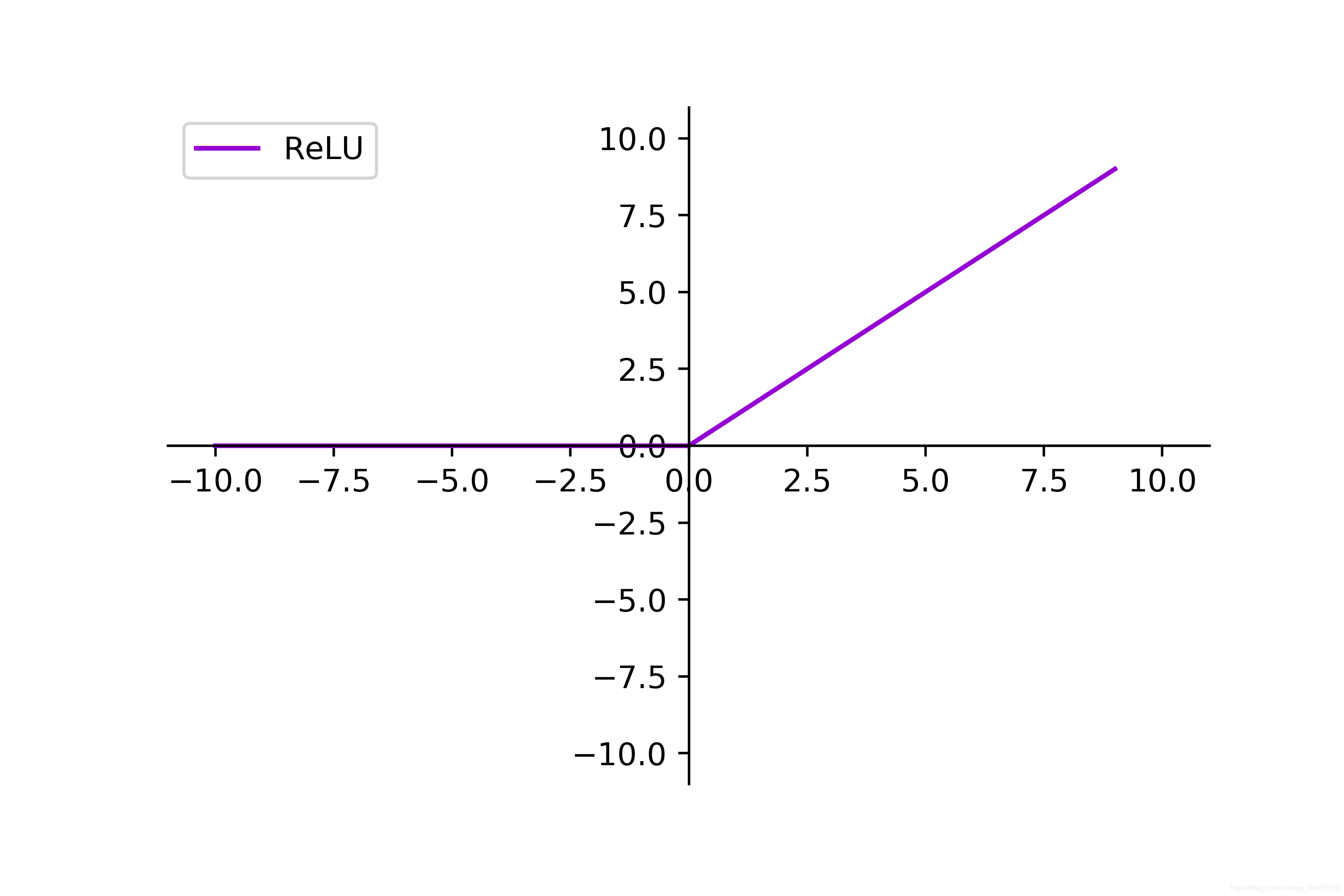
相比于Sigmoid函数,ReLU的主要优势在于它的计算速度更快且更容易收敛,并且在处理大规模数据和深层神经网络时表现更好。它解决了梯度消失问题,并且能够更好地适应非线性关系。
每种激活函数都有自己的特点和适用范围,在实际应用中,选择使用哪种激活函数取决于具体的问题和数据集特征。如果需要将输出转化为概率值,Logistic回归中的Sigmoid函数是一个不错的选择。如果需要处理更复杂的非线性关系,深度学习中的ReLU函数可能更适合。
Logistic回归实例
1. 数据预处理
首先,我们需要加载数据集,数据使用Scikit-learn里的鸢尾花数据集(Iris Dataset)。在Scikit-learn中,可以使用load_iris()函数来加载数据集。为了简化问题,我们只使用两个特征:萼片长度(sepal length)和花瓣长度(petal length)。同时,我们只考虑两个类别:山鸢尾(Iris-setosa)和变色鸢尾(Iris-versicolor),并将它们分别标记为0和1。
from sklearn.datasets import load_iris
import numpy as np
iris = load_iris()
X = iris.data[:, [0, 2]]
y = (iris.target != 0) * 1
print('Number of examples:', len(y))
print('Number of features:', X.shape[1])
print('Classes:', np.unique(y))
输出:
2. 模型定义
接下来,我们定义Logistic回归模型。
def sigmoid(x):
return 1 / (1 + np.exp(-x))
class LogisticRegression:
def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
self.lr = lr
self.num_iter = num_iter
self.fit_intercept = fit_intercept
self.verbose = verbose
def __add_intercept(self, X):
intercept = np.ones((X.shape[0], 1))
return np.concatenate((intercept, X), axis=1)
def __loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def fit(self, X, y):
if self.fit_intercept:
X = self.__add_intercept(X)
self.theta = np.zeros(X.shape[1])
for i in range(self.num_iter):
z = np.dot(X, self.theta)
h = sigmoid(z)
gradient = np.dot(X.T, (h - y)) / y.size
self.theta -= self.lr * gradient
if self.verbose and i % 10000 == 0:
z = np.dot(X, self.theta)
h = sigmoid(z)
print('loss: ', self.__loss(h, y))
def predict_prob(self, X):
if self.fit_intercept:
X = self.__add_intercept(X)
return sigmoid(np.dot(X, self.theta))
def predict(self, X, threshold=0.5):
return self.predict_prob(X) >= threshold
3. 训练模型
现在,我们可以通过调用LogisticRegression类来训练模型。我们将样本分成训练集和测试集,使用训练集来训练模型,并使用测试集来评估模型性能。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
model = LogisticRegression(lr=0.1, num_iter=300000)
model.fit(X_train, y_train)
print('Training accuracy:', (model.predict(X_train) == y_train).mean())
print('Test accuracy:', (model.predict(X_test) == y_test).mean())
输出:

4. 结果可视化
最后,我们可以将模型的决策边界可视化。由于我们只使用了两个特征,所以决策边界是一条直线。
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='viridis')
x1_min, x1_max = X[:, 0].min(), X[:, 0].max(),
x2_min, x2_max = X[:, 1].min(), X[:, 1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red')
输出:
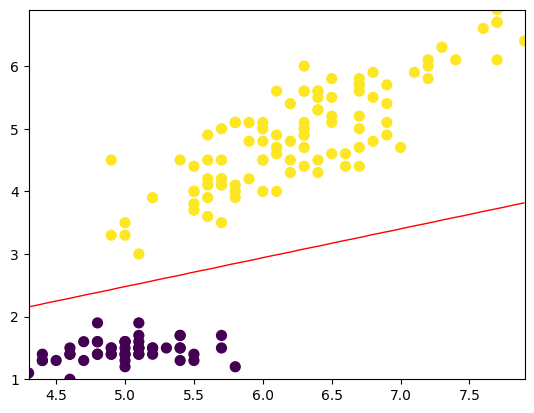
这个实例展示了如何使用Logistic回归算法来解决二分类问题。通过加载鸢尾花数据集,选择两个特征并标记两个类别,我们定义了LogisticRegression类来训练和预测模型。在这个简单的示例中,模型在训练集和测试集上都得到了100%的准确度,说明模型具有很好的适应能力和泛化能力。
需要注意的是,在实际应用中,需要考虑更多的因素,例如数据集的大小、特征的选择、模型的超参数等等。此外,在使用Logistic回归模型时,还需要进行特征缩放、正则化等处理,以提高模型的性能和泛化能力。
结语
Logistic回归是一种简单而有效的二元分类算法,它通过逻辑函数将线性回归的预测值转换为概率值。在实际应用中,Logistic回归通常与其他算法(如决策树和随机森林)结合使用,以提高分类的准确率。它也可以通过特征工程和正则化等方法进行改进,以适应不同的数据集和问题。同时,根据实际情况选择适当的激活函数,在解决其他分类问题时也是非常重要的。
希望这篇博客对你有所帮助!如果你有任何问题或疑惑,欢迎在下方留言讨论。