| 内容 | 1.括号匹配问题 |
| 2.最小栈 | |
| 3.最大栈 |
1.括号匹配问题
栈的典型题目还是非常明显的,括号匹配、表达式计算等等几乎都少不了栈,本小节我们就看两个最经典的问题
首先是LeetCode20,链接

本道题还是比较简单的,其中比较麻烦的是如何判断两个符号是不是一组的
我们可以用哈希表将所有符号先存储,左半边做key,右半边做 value。遍历字符串的时候,遇到左半边符号就入栈,遇到右半边符号就与栈顶的符号比较,不匹配就返回false
class Solution {
// 定义一个映射表,用于匹配括号
private static final Map<Character, Character> map = new HashMap<Character, Character>() {{
put('{', '}');
put('[', ']');
put('(', ')');
put('?', '?');
}};
public boolean isValid(String s) {
// 若字符串长度大于0且首字符不在映射表中,则直接返回false
if (s.length() > 0 && !map.containsKey(s.charAt(0))) {
return false;
}
// 使用链表作为栈的实现,初始化时添加一个占位符'?'
LinkedList<Character> stack = new LinkedList<Character>() {{
add('?');
}};
// 遍历字符串中的每个字符
for (Character c : s.toCharArray()) {
if (map.containsKey(c)) { // 若字符为左括号,则将其入栈
stack.addLast(c);
} else if (map.get(stack.removeLast()) != c) { // 若字符为右括号,则与栈顶字符进行匹配
return false;
}
}
// 最终,若栈中只剩下一个占位符'?',则所有括号都匹配成功
return stack.size() == 1;
}
}
这种问题使用java还是比较方便,但是对于C语言就非常不友好,需要自己构造,然后再实现算法。
LeetCode给我们制造了十几个括号匹配问题,但是都是条件变来变去,解决起来有难有易。
例如,LeetCode22链接
代码如下:
import java.util.ArrayList;
import java.util.List;
public class Solution {
// 做减法
public List<String> generateParenthesis(int n) {
List<String> res = new ArrayList<>();
// 特判
if (n == 0) {
return res;
}
// 执行深度优先遍历,搜索可能的结果
dfs("", n, n, res);
return res;
}
/**
* 执行深度优先遍历,搜索可能的括号组合
* @param curStr 当前递归得到的结果
* @param left 剩余可用的左括号个数
* @param right 剩余可用的右括号个数
* @param res 结果集
*/
private void dfs(String curStr, int left, int right, List<String> res) {
// 因为每一次尝试,都使用新的字符串变量,所以无需回溯
// 在递归终止的时候,直接把它添加到结果集即可,注意与「力扣」第 46 题、第 39 题区分
if (left == 0 && right == 0) {
res.add(curStr);
return;
}
// 剪枝(如图,左括号可以使用的个数严格大于右括号可以使用的个数,才剪枝,注意这个细节)
if (left > right) {
return;
}
if (left > 0) {
dfs(curStr + "(", left - 1, right, res); // 尝试放一个左括号
}
if (right > 0) {
dfs(curStr + ")", left, right - 1, res); // 尝试放一个右括号
}
}
}
LeetCode32最长有效括号

class Solution {
public int longestValidParentheses(String s) {
int maxans = 0; // 最长有效括号的长度
int[] dp = new int[s.length()]; // 用于存储以当前字符结尾的最长有效括号的长度
for (int i = 1; i < s.length(); i++) {
if (s.charAt(i) == ')') { // 当前字符为右括号时
if (s.charAt(i - 1) == '(') { // 前一个字符为左括号时
// 更新以当前字符结尾的最长有效括号的长度
dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
} else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
// 当前字符前面有一段有效括号,且该段有效括号前面是左括号时
// 更新以当前字符结尾的最长有效括号的长度
dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;
}
maxans = Math.max(maxans, dp[i]); // 更新最长有效括号的长度
}
}
return maxans; // 返回最长有效括号的长度
}
}
LeetCode301链接
class Solution {
private List<String> res = new ArrayList<String>(); // 用于存储有效的括号组合
public List<String> removeInvalidParentheses(String s) {
int lremove = 0; // 需要移除的左括号数量
int rremove = 0; // 需要移除的右括号数量
for (int i = 0; i < s.length(); i++) {
if (s.charAt(i) == '(') {
lremove++; // 统计左括号数量
} else if (s.charAt(i) == ')') {
if (lremove == 0) {
rremove++; // 统计右括号数量,如果没有对应的左括号,则需要移除该右括号
} else {
lremove--; // 匹配到一个右括号,可以抵消一个左括号
}
}
}
helper(s, 0, lremove, rremove); // 辅助函数进行递归处理
return res; // 返回有效的括号组合列表
}
private void helper(String str, int start, int lremove, int rremove) {
if (lremove == 0 && rremove == 0) { // 当需要移除的括号数量为0时,判断当前字符串是否有效
if (isValid(str)) {
res.add(str); // 如果有效,则将其添加到结果列表中
}
return; // 结束递归
}
for (int i = start; i < str.length(); i++) {
if (i != start && str.charAt(i) == str.charAt(i - 1)) {
continue; // 避免重复计算,如果当前字符和前一个字符相同,则跳过
}
// 如果剩余的字符无法满足去掉的数量要求,直接返回
if (lremove + rremove > str.length() - i) {
return;
}
// 尝试去掉一个左括号
if (lremove > 0 && str.charAt(i) == '(') {
helper(str.substring(0, i) + str.substring(i + 1), i, lremove - 1, rremove);
}
// 尝试去掉一个右括号
if (rremove > 0 && str.charAt(i) == ')') {
helper(str.substring(0, i) + str.substring(i + 1), i, lremove, rremove - 1);
}
}
}
private boolean isValid(String str) {
int cnt = 0; // 记录左括号和右括号的差值
for (int i = 0; i < str.length(); i++) {
if (str.charAt(i) == '(') {
cnt++; // 遇到左括号,增加差值
} else if (str.charAt(i) == ')') {
cnt--; // 遇到右括号,减少差值
if (cnt < 0) {
return false; // 如果差值小于0,说明右括号多余左括号,无效
}
}
}
return cnt == 0; // 差值为0,说明左右括号一一对应,有效
}
}
2.最小栈
LeetCoede155链接

本道题的关键在于理解getMin()到底表示什么,可以看一个例子上的示例画成示意图如下:
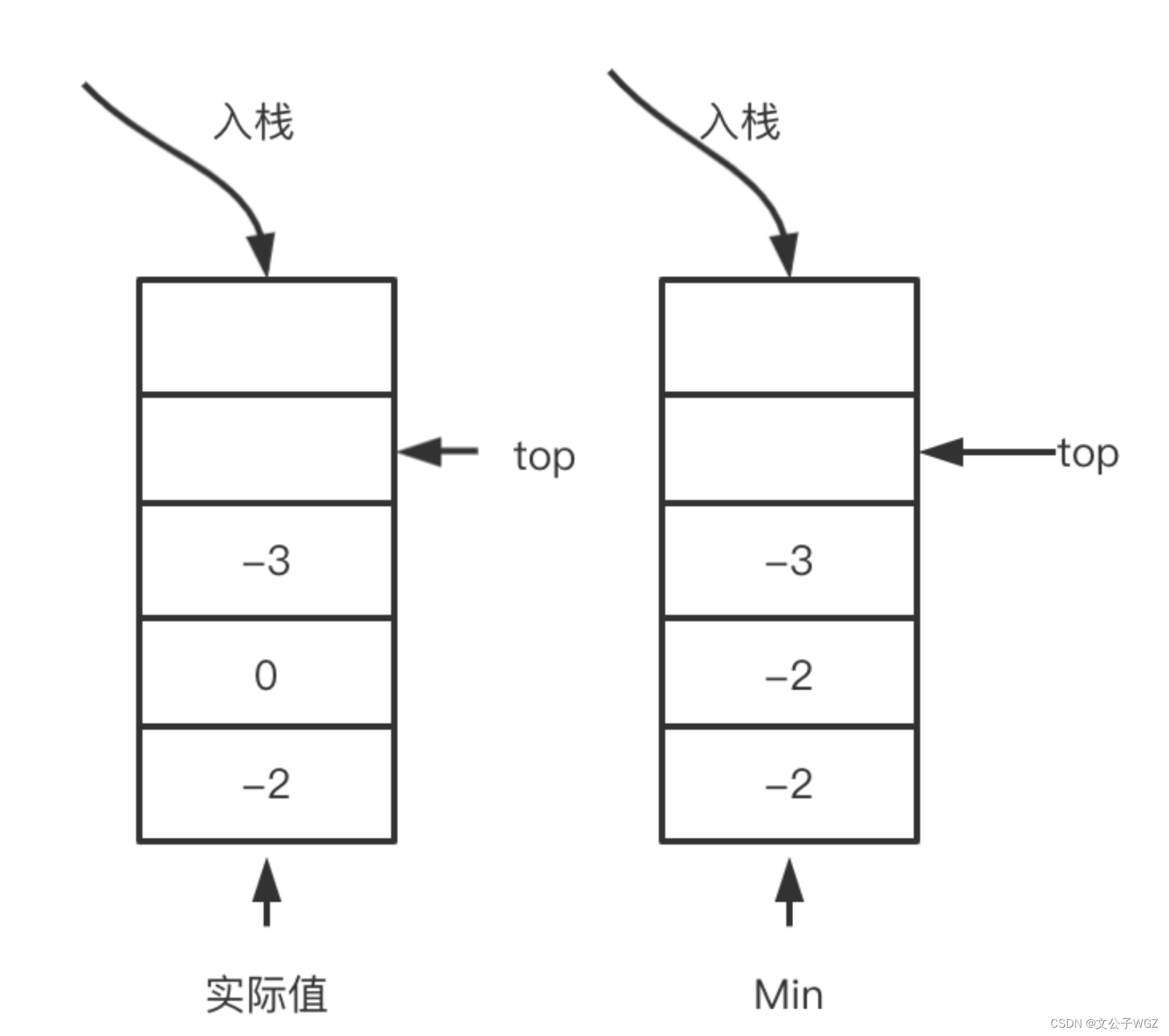
这里的关键是理解对应的Min栈内,中间元素为什么是-2,理解了本道题就非常简单。
题目要求在常数事件内获得栈的最小值,因此不能在getMin()的时候再去计算最小值,最好在push或者pop的时候就已经计算好了当前栈中的最小值。
对于栈来说,如果一个元素a在入栈时,栈里有其他元素的b,c,d,那么无论这个栈在之后经历了什么操作,只要a在栈中,b,c,d就一定在栈中,因为在a被弹出之前,b,c,d就不会被弹出。
那么,我们可以在每个元素a入栈的时候把当前栈的最小值m存储起来,在这之后无论何时,如果栈顶元素是a,我们就可以直接返回存储的最小值m。
按照上面的思路,我们只需要设计一个数据结构,使得每一个元素a与其相应的最小值m时刻保持一一对应,因此我们使用一个辅助栈,与元素栈同步插入与删除,用于存储与每个元素对应的最小值。
- 当一个元素要入栈的时候,我们取当前辅助栈的栈顶存储的最小值,与当前元素比较得出最小值,将这个最小值插入辅助栈中。
- 当一个元素要出栈的时候,我们把辅助栈的栈顶元素也一并弹出。
- 在任意一个时刻,栈内元素的最小值就存储在辅助栈的栈顶元素中。
/**
* 实现一个最小栈 MinStack,支持 push、pop、top 和 getMin 操作
*/
class MinStack {
private Stack<Integer> stack; // 存储栈元素的主栈
private Stack<Integer> min_stack; // 存储当前栈中最小值的辅助栈
public MinStack() {
stack = new Stack<>();
min_stack = new Stack<>();
}
/**
* 向栈中压入元素x
* @param x 待压入的元素
*/
public void push(int x) {
stack.push(x); // 将元素压入主栈中
if (min_stack.isEmpty() || x <= min_stack.peek()) {
min_stack.push(x); // 如果是最小值,则将其压入辅助栈中
}
}
/**
* 弹出栈顶元素
*/
public void pop() {
if (stack.pop().equals(min_stack.peek())) {
min_stack.pop(); // 如果是最小值,则从辅助栈中弹出
}
}
/**
* 获取栈顶元素
* @return 栈顶元素
*/
public int top() {
return stack.peek(); // 直接返回主栈的栈顶元素
}
/**
* 获取栈中最小值
* @return 栈中最小值
*/
public int getMin() {
return min_stack.peek(); // 直接返回辅助栈的栈顶元素,即为栈中最小值
}
}
3.最大栈
LeetCode716.设计一个最大栈数据结构,既支持栈操作,又支持查找栈中的最大元素。
实现MaxStack类:
MaxStack()初始化栈对象
void push(int x)将元素x压入栈中。
int pop()移除栈顶元素并返回这个元素
int top()返回栈顶元素,无需移除
int peeMax()检索并返回栈中最大元素,无需移除。
int popMax()检查并返回栈中最大元素,并将其移除。
如果有多个元素,只要移除 最靠近栈顶的那个。示例:
输入:
["MaxStack","push","push","top","popMax","top","premix","pop","top"]
[[],[5],[1],[5],[],[],[],[],[],[]]
输出:
[null,null,null,null,5,5,1,5,1,5]
解释:
MaxStack stk=new MaxStack();
stk.push(5); //[5] - 5既是栈顶元素,也是最大元素
stk.push(1); //[5,1】 - 栈顶元素是1,最大元素是5
stk.push(5); //[5,1,5] - 5既是栈顶元素,也是最大元素
stk.top(); //返回 5,[5,1,5] - 栈没有改变
stk.popMax(); //返回 5,[5,1] - 栈发生改变,栈顶元素不再是最大元素
stk.top(); //返回 1,[5,1] - 栈没有改变
stk.popMax(); //返回 5,[5,1] - 栈没有改变
stk.pop(); //返回 1,[5] - 次操作后,5既是栈顶元素,也是最大元素
stk.top(); //返回5,[5] - 栈没有改变本道题与上一题相反,但是处理方法是一致的,一个普通的栈可以支持前三种操作push(x)、pop()和top(),所以我们需要考虑的仅仅为后两种操作的peekMax()和popMax()。
对于peekMax(),我们可以另一个栈来存储每个位置到栈底的所有元素的最大值,例如,如果当前的第一个栈中元素为[2,1,5,3,9],那么第二个栈中的额元素为[2,2,5,5,9]。在push(x)操作时,只需要将第二个栈的栈顶和x的最大值入栈,而在pop()操作时,只需要将第二个栈进行出栈。
对于popMax(),由于我们知道当前栈中最大的元素值,因此可以直接将两个栈同时出栈,并存储第一个栈出栈的所有值。当某个时刻,第一个栈的出栈元素就等于当前栈中最大的元素值时,就找到了最大的元素。这个时候我们将之前第一个栈的所有元素重新入栈,并且同步更新第二个栈,就完成了popMax()操作。
package com.yugutou.charpter4_stack.level2;
import java.util.Stack;
/**
* 实现一个支持 push、pop、top、peekMax 和 popMax 操作的最大栈 MaxStack
*/
class MaxStack {
Stack<Integer> stack; // 存储栈元素的主栈
Stack<Integer> maxStack; // 存储当前栈中最大值的辅助栈
public MaxStack() {
stack = new Stack(); // 初始化主栈
maxStack = new Stack(); // 初始化最大值辅助栈
}
/**
* 向栈中压入元素x
* @param x 待压入的元素
*/
public void push(int x) {
int max = maxStack.isEmpty() ? x : maxStack.peek(); // 获取当前最大值
maxStack.push(max > x ? max : x); // 将当前最大值或新元素压入最大值辅助栈
stack.push(x); // 将元素压入主栈
}
/**
* 弹出栈顶元素
* @return 弹出的栈顶元素
*/
public int pop() {
maxStack.pop(); // 弹出最大值辅助栈的栈顶元素
return stack.pop(); // 弹出主栈的栈顶元素
}
/**
* 获取栈顶元素
* @return 栈顶元素
*/
public int top() {
return stack.peek(); // 直接返回主栈的栈顶元素
}
/**
* 获取栈中最大值
* @return 栈中最大值
*/
public int peekMax() {
return maxStack.peek(); // 直接返回最大值辅助栈的栈顶元素,即为栈中最大值
}
/**
* 弹出栈中的最大值
* @return 被弹出的最大值
*/
public int popMax() {
int max = peekMax(); // 获取当前栈中的最大值
Stack<Integer> buffer = new Stack(); // 辅助栈用于暂存元素
while (top() != max) {
buffer.push(pop()); // 将非最大值的元素暂存到辅助栈中
}
pop(); // 弹出栈中的最大值
while (!buffer.isEmpty()) {
push(buffer.pop()); // 将暂存的元素重新压入栈中
}
return max; // 返回被弹出的最大值
}
}
学习算法的时候真的是很费脑,但是看懂之后又觉得自己很厉害,自己走了很多步,再回头看,原来也不过如此,敢于尝试真的是勇敢的象征。