相关数据集的下载:https://www.sintef.no/projectweb/top/pdptw/100-customers/

由于Li&Lim生成测试实例的方式，这些实例中的任务数量不同，略高于标称值。
在这里，您可以找到Li&Lim的PDPTW基准问题的100个任务实例的实例定义和最著名的解决方案（据我们所知）。此处报告的版本有一个层次目标：1）尽量减少车辆数量2）尽量减少总距离。距离和时间应以双倍精度计算，总距离结果四舍五入到两位小数。精确方法通常使用总距离目标，并使用积分或低精度距离和时间计算。因此，结果无法直接比较。

《A survey on pickup and delivery problems》

Parragh, S.N., Doerner, K.F. & Hartl, R.F. A survey on pickup and delivery problems . Journal für Betriebswirtschaft 58, 81–117 (2008). https://doi.org/10.1007/s11301-008-0036-4
原文链接: Published: 16 May 2008 SPringer

摘要

本文是对涉及提货和交货的路线问题进行全面调查的第二部分。基本上，可以区分两类问题。第一部分涉及从仓库到长途客户和从回程客户到仓库的货物运输。第二部分现在考虑货物在提货和交货地点之间运输的所有问题，称为提货和交货车辆路径问题（VRPPD）。这些问题包括取车和交付车辆路线问题（PDVRP–未配对取车和交货点）、经典的取车和发货问题（PDP–配对取车点和交货点之间）和拨号侧问题（DARP–配对取货和交货点间的乘客运输以及考虑到的用户不便）。给出了所有三种VRPPD类型的单车辆和多车辆数学问题公式，并讨论了各自的精确、启发式和元启发式求解方法。

1 Basic definitions

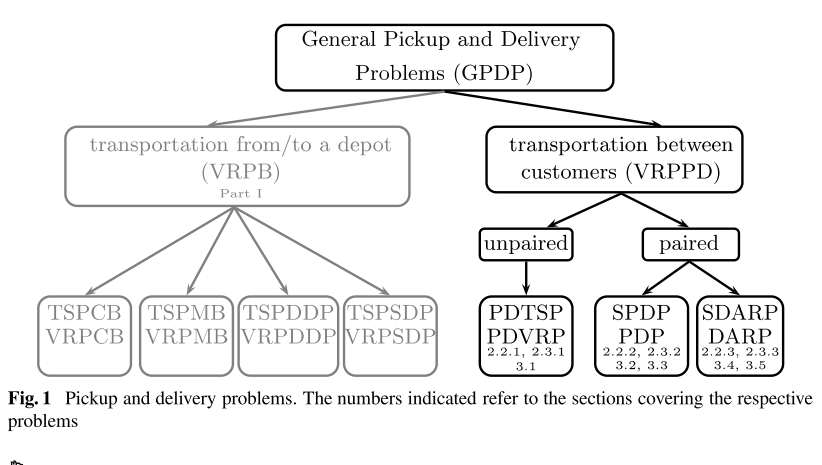
本文的目的是提出一种分类方案，并对提货和交货问题及其变体进行全面调查。本调查的第一部分介绍了属于回程车辆路线问题（VRPB）类别的所有问题类型，其中货物从仓库运输到长途客户，以及从回程客户运输到仓库。此外，还提出了这项调查的动机。第二部分涵盖货物在提货地点和交货地点之间运输的所有问题类型，称为提货和交货车辆路线问题（VRPPD）。

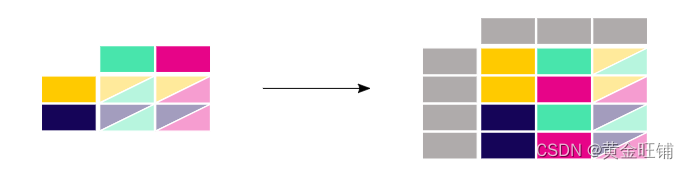
图1描述了两个提货和交货问题类及其子类。灰色部分在本调查的第一部分中进行了讨论。方框中的数字指定了涵盖各个问题的章节。前两个指标涉及建模部分，而最后一个指标涉及解决方法部分。

1.1 VRPPD subclass definition

我们所称的VRPPD类是指货物从提货点运输到交货点的问题。它可以进一步分为两个子类。第一个子类是指提货和交货地点不成对的情况。这是一种同质的商品。每个提货单元可用于满足任何交货客户的需求。在文献中，大多数单车案例都是固定的，表示为带能力的旅行推销员问题（Anily和Bramel，1999年）、一个商品取件和送货旅行推销员问题问题（1-PDTSP）（Hern´andez-P´erez和Salazar Gonz´alez，2003年）以及旅行推销员问题，包括取件和发货问题（Hern‘andez-P‘erez和Salazar Gonz-alez 2004a）。由于文献中也报道了多车辆应用（参见Dror等人，1998），我们将在多车辆和单车辆情况下分别将该问题分类为取件和配送车辆路线问题（PDVRP）Pickup and Delivery Vehicle Routing Problem 和取件和交付旅行推销员问题（PDTSP）Pickup and Delivery Traveling Salesman Problem。

第二个VRPPD子类包括经典的拾取和传送问题（PDP）和拨号侧问题（DARP）。这两种类型都考虑运输请求，每个请求都与出发地和目的地相关联，从而产生成对的取件点和交货点。PDP负责货物运输，DARP负责客运。这种差异通常以明确考虑用户便利性的附加约束或目标来表示。PDP的单车变体也被称为取货-送货旅行推销员问题（Kalantari等人，1985年），多车案例被称为带有取货和送货的车辆路线问题（Derings和D¨ohmer，2008年）。然而，大多数已发表的工作都将这类问题称为提货和交货问题（PDP）（参见例如Dumas等人1991；van der Bruggen等人1993）。我们将遵循此命名。拨号乘车问题也大多被称为此类问题。然而，一些作者，如Toth和Vigo（1996），指出了与残疾人交通问题相同的问题。动态版本也被称为需求响应型运输（例如，Mageen和Nelson 2003）。我们注意到PDP的单车案例称为SPDP，DARP的单车案例为SDRP。

1.2 Limitations

在运输领域，可以区分两类问题：满载问题和少载问题。满载问题涉及单位容量的车辆以及每个客户地点的单位需求或供应。在成对的拾取和递送位置的情况下，在取货和其关联的交货地点之间不能访问其他客户（见Archetti和Sper-anza 2004；Coslovich等人2006a；Currie和Salhi 20032004；de Meulemeester等人1997；Doerner等人2001；Fleischmann等人2004；Gronalt等人2003；Gronal和Hirsch 2007；Imai等人2007；Jordan和Burns 1984；Jordan 1987；Powell等人19952000a，2000b；Regan等人1996a，1996b，1998；Russell和Challinor 1988；Wang和Regan 2002；Yang等人1998；2004等）.

此外，存在一个问题类别，根据定义，该问题类别不属于满载类别，因为考虑了容量为2的车辆。然而，这些问题与满载类别密切相关，因为它们来自相同的应用领域（集装箱调度）。本文的目的是提出一个简明的分类方案和调查，仅限于涉及提货和交货操作的车辆路线问题，其中路线而不是调度问题是最重要的因此，本文将不介绍满载调度方法以及与该类密切相关的方法。（例如，见Archetti等人2005；勒布朗克等人2006）。此外，关于顺序问题的文献，例如，在联运站出现的，涉及门式起重机装卸和运输操作的文献（例如，B–ose等人，19992000；Gutenschwager等人，2003）也不属于本调查的一部分。

1.3 Structure of the survey

本文的其余部分组织如下。首先，为了明确定义不同的VRPPD类型，给出了单车辆和多车辆情况下一致的数学问题公式。然后，在相应问题的小节中讨论了解决方法。在每一小节中，给出了精确、启发式和元启发式解决方法。还将提及相关工作。第4节概述了不同问题类的现有基准实例，以及一些已知解决方案的信息。本次调查的最后给出了结论和未来研究的可能方向。

2 Mathematical problem formulation

在下一节中，将提出一致的数学问题公式。首先，给出了整个调查过程中使用的符号。之后，介绍了两种基本的问题公式，一种用于单车辆，另一种用于多车辆情况。这些问题分别针对未配对的取车和配送问题、经典的取车与配送问题和拨号乘车问题进行了调整。注意，数学模型仅用于定义目的, 减去其LP松弛的强度，或者它们是否用于加法边界、分支和切割算法或拉格朗日松弛。我们请感兴趣的读者参考精确解决程序章节中总结的工作，以了解有关这些方面的更多信息。所有定义的问题都是NP难的，因为它们概括了众所周知的旅行推销员问题（TSP）（Garey和Johnson 1979）。

2.1 Notation

注意符号的对称和不对称的有效性.

• $t_{ij}^k=t_{ji}^k$ 表示车辆k在i和j之间的行驶时间
• $c_{ij}^k=c_{ji}^k$表示车辆k在弧(i,j)之间的成本

VRPPD可以看成一个完全图$G=(V,A)$, V = { 0 , n + n ~ + 1 } ∪ P ∪ D V=\{0,n+\tilde{n}+1\} \cup P\cup D V={0,n+n~+1}∪P∪D表示顶点集,$A=\{(i,j):i,j\in V,i\ne n+\tilde{n}+1,j\ne 0,j\ne i\}$表示弧集

在优化过程中，根据所考虑的问题，确定以下一些或所有决策变量。

请注意，依赖于车辆的起点和终点可以很容易地引入到模型中。然而，为了简单起见，我们在公式中不考虑这个扩展。在单车问题公式中，可以省略上标k，从而得到参数系数$c_{ij}、t_{ij}、C、T$和决策变量$x_{ij}、Q_i、B_i$。

2.2 Single vehicle pickup and delivery problem formulations

不同VRPPD的单车模型基于开放式TSP公式。对于$\forall S\subseteq V,A=(S,\bar{S})=\{(i,j)\in A:I\in S,j\notin S\}$.然后,则开放的TSP假设为:

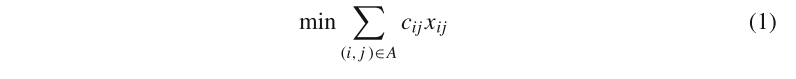
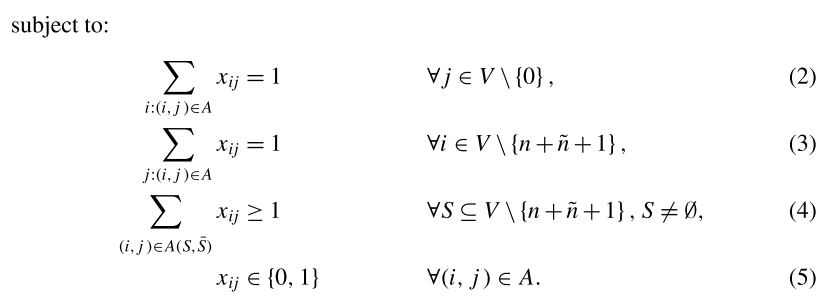
目标函数（1）使总路由成本最小化。
等式（2）和（3）确保每个顶点访问一次。
约束（4）是确保路线连通性的几种可能性之一。

2.2.1 PDTSP

这里假设每一个提货单位都能满足每一个交货客户的需求。与本调查第一部分所述的TSPMB相似，车辆荷载限制必须修改为公式（1）-（5），

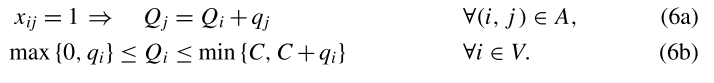
与TSPMB不同的是，车辆的初始载荷在这里是自由的（参见Hern´andez-P´erez和Salazar Gonz´alez 2004a）。此外，PDTSP（PDVRP）是（6a）中唯一需要等式的VRPPD类，对于所有其他问题类型，“≥”符号就足够了

$x_{ij}=1$是决策变量,表示从i经过j.修改为$Q_j=Q_i+q_j$,在i点车的存货+在j点的需求任务=在j点的存货.要在i点可以完成接下来的j点的任务,则$Q_i$需要满足,如果是卸载的时候$q_i>0$,则当前的存货应大于$|q_i|$,既有 m a x { 0 , q i } max\{0,q_i\} max{0,qi​}. 如果是装载的时候$q_i<0$,则当前的存货应该小于$c+q_i$.即可得(6b).

2.2.2 SPDP

SPDP考虑拾取和传送顶点成对的情况，即$n=\tilde{n}$。在文献中，通常将这样的顶点对称为request请求。$i=1,\cdots ,n$，其中i是起点或拾取点，$n+i$是相应的目的地或递送点。为了确保每个目的地仅在其出发地之后访问，除了（1）–（3）、（5）和（6）之外，还需要优先约束，这些约束通常通过时间变量建模，

约束条件（7）规定每个出发地都要在目的地之前访问，（8）确保时间变量与旅行和服务时间一致。注意，（8）还保证避免了短周期，因此不需要不等式（4），假设$（t_{ij}+d_i）$对所有$（i，j）\in A＞0$。

2.2.3 SDARP

SDARP涉及人员运输。这类问题会出现，例如，与残疾人或老年人的交通有关。然而，另一种可能的应用是易腐货物的运输，这也需要最大的乘车时间限制。除了（1）-（3）和（5）-（8）中给出的基本模型外，还必须考虑用户的不便。这可以通过目标函数中的另一项或附加约束来处理。这里，我们选择制定最大用户乘坐时间限制，

2.2.4 Time window constraints

关于遵守时间窗（TW）的约束，

可以添加到所有上述制剂中。在客运方面，TW通常存在。注意，由于约束（6a）和（8），上述公式不是线性的。可以使用大M公式对其进行线性化（参见Cordeau 2006）。

2.3 Multi vehicle pickup and delivery problem formulations

多车辆取送问题的基本模型是一个适用于三指标车辆路径问题的公式，该公式与Cordeau等人（2002年，第158f页）为VRPTW提出的公式相同。

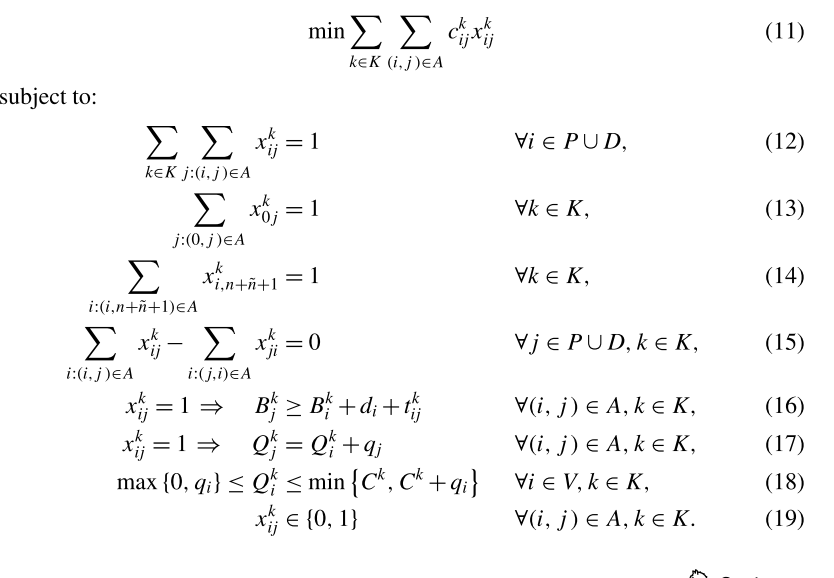
目标函数（11）使总路由成本最小化。约束（12）规定每个顶点必须被精确地服务一次。等式（13）和（14）保证每辆车从车辆段出发，并在其路线结束时返回车辆段。请注意，这并不意味着必须使用每辆车。车辆只能使用弧线$（0，n+\tilde{n}+1）$，即不离开车辆段。（15）确保了流量守恒。时间变量用于消除（16）中的子时间，假定$（t_{ij}^k+d_i)>0,\forall (i,j)\in A$.约束条件（17）和（18）保证车辆在整个行程中不超过其容量。应注意，该公式需要引入额外的决策变量 $Q_i^k$，对应于车辆k在顶点i处的总负载。这些变量不需要用于公式化基本VRP，但对于将其扩展到提货和交货问题是必不可少的。在VRP公式中，有时使用类似于（17）的不等式来确保路线连通性（由上述公式中的（16）完成）。此外，在（17）中，仅PDVRP（PDTSP）需要相等。对于所有其他VRPPD类型，可以用“≥”代替。

（16）和（17）中给出的非线性约束可以使用大M公式进行线性化（参见Cordeau 2006）。

2.3.1 PDVRP

PDVRP的特殊之处在于，每一台设备都能满足每一位客户的需求。上述公式（11）-（19）已经是PDVRP的适当公式。不需要额外的调整。

2.3.2 PDP

这里，每个提货点都与一个交货点相关联，因此$n=\tilde{n}$。除了（11）–（19）之外，还需要两组约束条件。首先，请求的始发地和目的地必须由同一车辆提供服务，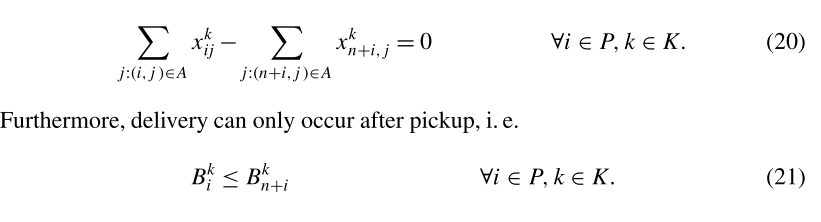

2.3.3 DARP

为了将多车辆PDP扩展到多车辆DARP，再次如在单车辆情况下一样，需要添加与用户不便相关的约束。对于单车版本，我们将限制这一要求，在公式（11）-（21）中增加最大用户乘坐时间限制：

2.3.4 Additional constraints

另外两组约束可以添加到上述所有问题类中。这些是时间窗口和最大路由持续时间限制，

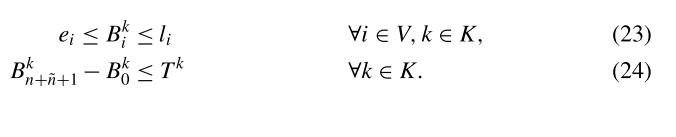
3 Solution methods for VRPPD

在下一节中，将概述PDVRP、PDP和DARP的不同解决方法。解决方法分为精确、启发式和元启发式方法。第4节对所使用的基准实例进行了描述。有关所应用的解决方案概念的一般信息，请参阅本文的第一部分。Bereglia等人（2007）对不同解决方法进行了另一项调查。由于最大纸张长度的限制，无法详细描述所有发表的作品。本文以表格的形式对所提出的方法进行了概述。仅对我们认为特别重要的贡献（出于近期或原创性原因）进行了更详细的描述。这些在不同的表格中用星号标记。解决方法在表中按时间顺序排列，根据单车辆和多车辆方法。关于解算法的更多细节以相同的顺序给出.

3.1 Unpaired pickups and deliveries

PDVRP，即每一件商品都可以在任何地方提取和运输的问题类，在文献中没有像其他问题类那样受到关注。此外，大多数文献仅限于PDTSP。因此，除Dror等人（1998）外，所提出的所有解决方法仅适用于一辆车的情况。据作者所知，迄今为止，还没有提出过PDTSP的元启发式方法。

3.1.1 Exact methods

Hern´andez-P´erez和Salazar Gonz´alez（20032004a）介绍了针对当前问题提出的唯一精确方法。这是一种分支切割算法。为了加快算法的构建和改进，应用了启发式算法。它们用于从当前节点的LP松弛解中获得可行解。构造启发式是最近插入算法的一种适应。它通过2-opt和3-opt交换得到改进（Lin 1965）。解决的测试实例是Mosheiov（1994）和Gendreau等人（1999）中使用的测试实例的改编，包含多达75个客户。

3.1.2 Heuristics

Chalasani和Motwani（1999）中考虑了PDTSP的一个特例；待提货的货物数量等于待交付的货物数量；每个交货（提货）地点的需求（供应）等于1。该问题是交换问题的扩展，其中车辆的容量也设置为1。Chalasani和Motwani提出了一种最坏情况界限为9.5的近似算法。他们使用Christofides的启发式方法（Christofides 1975）构建了两个旅行推销员之旅，一个只包含取货地点，一个仅包含发货地点。然后通过分解和匹配的方式将这两个游览组合起来。Anily和Bramel（1999）针对同一问题设计了一种多项式时间迭代巡回匹配算法。

在Hern´andez-P´erez和Salazar Gonz´alez中可以找到两种启发式方法（2004b）。第一种算法是构造改进型，使用贪婪构造过程，通过2-opt和3-opt交换进行改进。第二种方法基于不完全优化；Hern´andez-P´erez和Salazar Gonz´alez（2004a）中描述的分支和切割程序用于与有前景的边缘相关的变量数量减少。解决了多达500个客户的随机实例。

Lim等人（2005）提出了树图上的近似算法。它基于一个反复的施工过程，最坏情况下的界限为2。

Wang等人（2006）也对树和线上的PDTSP进行了研究。他们提出了一种用于线情况(line case)的$O（|V|2/minC，|V|）$算法。单位容量以及无容量版本可以在线性时间内解决。在一棵树上为无行为能力的案件准备。针对单位容量的情况，设计了$O（|V|）$算法和$O（|V{|}^2）$算法.

最后，Dror等人（1998）提出了一种启发式算法，用于将多车辆PDVRP应用于自助服务车的重新分配。这与Dijkstra的算法有关（Dijkstra1959）。此外，还简要讨论了其他解决方法。

3.2 The static pickup and delivery problem

本节介绍了典型的提货和交货问题（PDP）的解决方法，其中每个运输请求都与提货和交货点相关。Lokin（1978）是第一个讨论将优先约束纳入传统TSP的人，需要制定PDP。在Savels-bergh和Sol（1995）中首次尝试以统一符号概括PDP，涵盖了PDP的所有可能版本，包括拨号乘车问题。它们还简要概述了1995年以前的现有解决方法。Mitrovi´c-Mini´c（1998）提出了一项关于时间窗口PDP（PDPTW）的调查。Desrochers等人（1988年）对包括PDP在内的车辆路线问题进行了早期调查。Cordeau等人（2004）审查了需求响应型运输，包括PDP和DARP。Cordeau等人（2007）对最近专注于精确方法的工作进行了回顾。Assad（1988）、Desaulniers等人（2002）和Desrochers等人（1988）对解决方法进行了进一步调查。在以下段落中，根据精确、启发式和元启发式方法总结了静态PDP的各种解决方法。

3.2.1 Exact methods

已经为静态PDP提出了许多精确的求解程序。表1简要描述了不同的技术。给出了文献参考、目标和考虑的其他约束条件。此外，还提供了所使用的基准实例，或以请求数量计算的最大优化实例的大小。标有星号的条目将在下面进一步详细说明。

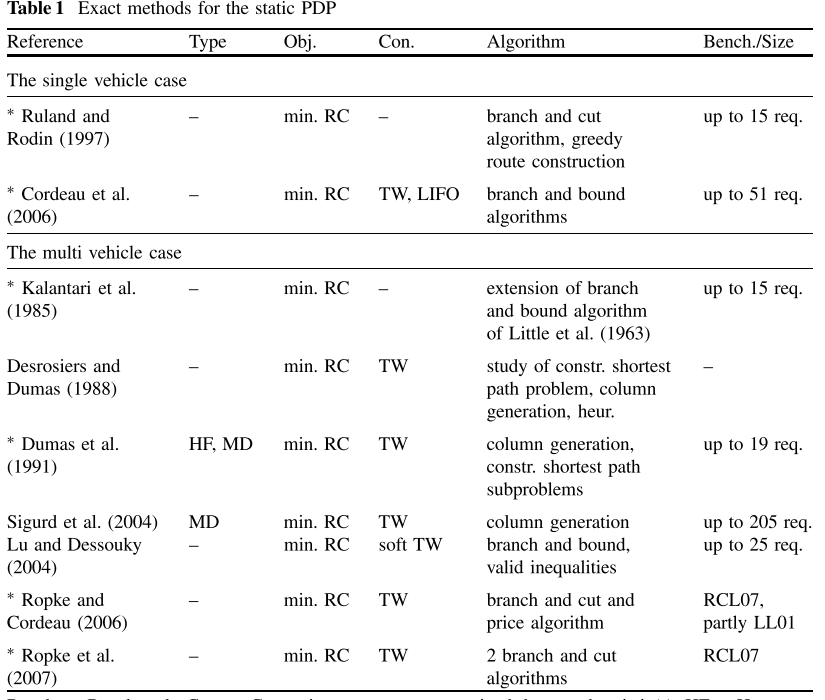
Bench. = Benchmark, Con. = Constraints, constr. = constrained, heur. = heuristic(s), HF = Heteroge- neous Fleet, LIFO = Last-In-First-Out, MD = Multi depot, Obj. = Objective(s), RC = Routing Cost, req. = requests, TW = Time Windows; The respective benchmark instances are described in Section 4. Entries marked by an asterisk (∗) are described in further detail in the text.

Ruland和Rodin（1997）提出了一种分支和切割算法来解决SPDP。它包括在边界阶段生成切割平面以及生成第一上界的贪婪路线构建过程。

Cordeau等人（2006）报道了一种具有后进先出（LIFO）装载的单车PDPTW的分支定界算法，即货物必须按照提货的相反顺序交付。他们提出了三个数学问题公式和各种有效的不等式。这些是基于PDP的现有等式和新的问题特定等式。

适用于单车辆和多车辆情况的第一种精确解方法可追溯到Kalantari等人（1985）。所描述的分支定界算法是Little等人（1963）开发的算法的扩展。

Dumas等人（1991）阐述了列生成方法。他们考虑了异构车辆、时间窗口以及多个仓库。利用正向动态规划算法求解约束最短路径问题。

Ropke和Cordeau（2006）引入了一种具有额外有效不等式的分支和定价算法。具有时间窗、容量、提货和交货限制的基本约束最短路径问题是PDPTW的自然定价问题。通过标签设置最短路径算法来解决该问题。有效的不等式以分支和切割的方式添加；讨论了它们对定价问题结构的影响。

Ropke等人（2007）研究了两种不同的2指数PDPTW公式的分支和切割算法。公式一利用时间变量。在公式中，通过不可行路径不等式对两个与时间相关的约束进行建模。后一种公式被证明在用作分支和切割算法的基础时更有效。还讨论了新的有效不等式，以加强所提出的公式。

3.2.2 Heuristics

静态PDP的启发式在20世纪80年代首次被提出。表2概述了此后开发的各种启发式解决方案技术。给出了所考虑的问题类型、使用的目标、附加约束、所提出的算法类型以及所解决的基准实例或为测试目的考虑的最大实例的信息。


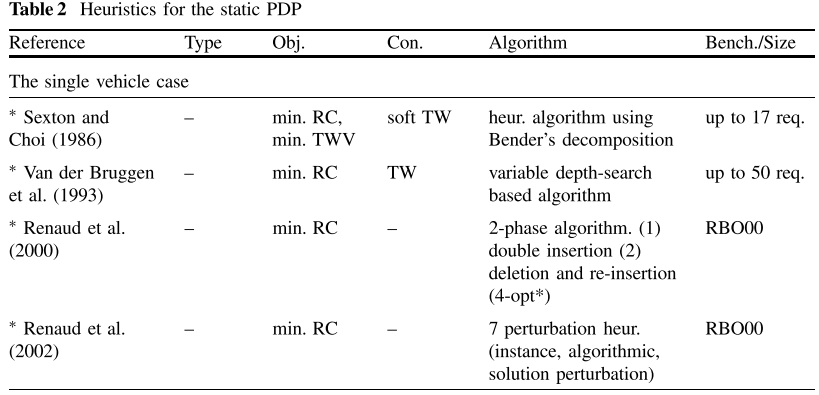
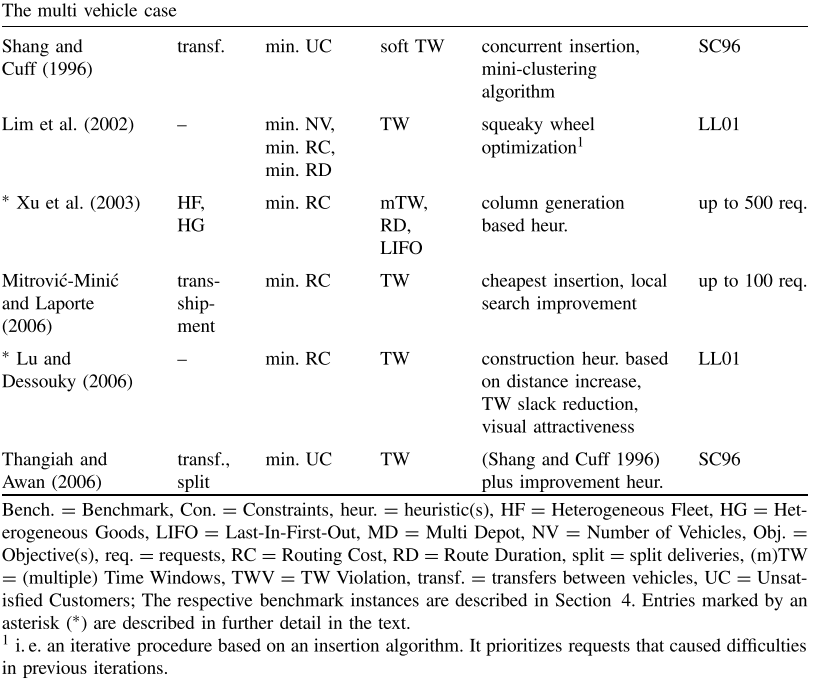
Sexton和Choi（1986）使用Bender分解程序近似求解静态SPDP。使用时空启发式构造初始解。路线改进阶段基于Bender分解。由于考虑了软时间窗口，目标函数考虑了总操作时间以及时间窗口违规处罚。

van der Bruggen等人（1993）讨论了静态SPDP的构造改进启发式算法。首先，构造可行的初始解。然后，通过交换程序始终保持可行性来改进此解决方案。

Renaud等人（2000）还针对相同的问题提出了一种构造改进算法。他们使用通过删除和重新插入改进的双插入构造启发式（4-opt*（Renaud等人，1996））。

Renaud等人（2002）提出了七种不同的扰动启发式方法，以生成静态SPDP的近似最优解。在所有七种实现中，首先，计算初始解，该初始解通过4-opt**启发式算法（4-opt*启发式算法的自适应）进行改进，从而始终遵守优先约束。然后，应用扰动方案（例如，算法或解扰动），然后是后优化阶段。重复最后两个步骤，直到使用两种启发式方法，即合并和两阶段，即合并行程和贪婪删除和插入请求。

Lu和Dessouky（2006）详细阐述了一种构造启发式。它不仅将企业距离增加纳入评估标准，还将减少时间窗口松弛以及视觉吸引力（称为交叉长度百分比）。

3.2.3 Metaheuristics

表3概述了为静态PDP提出的不同元启发式解决方法。对于每个参考，提供了与前表中相同的信息。


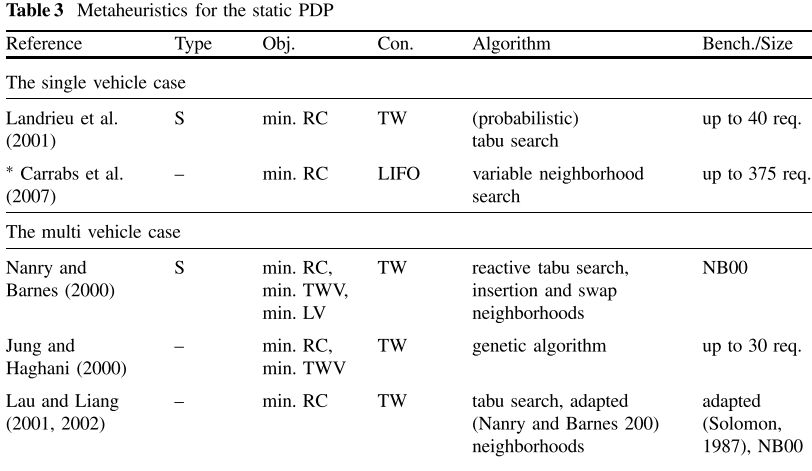
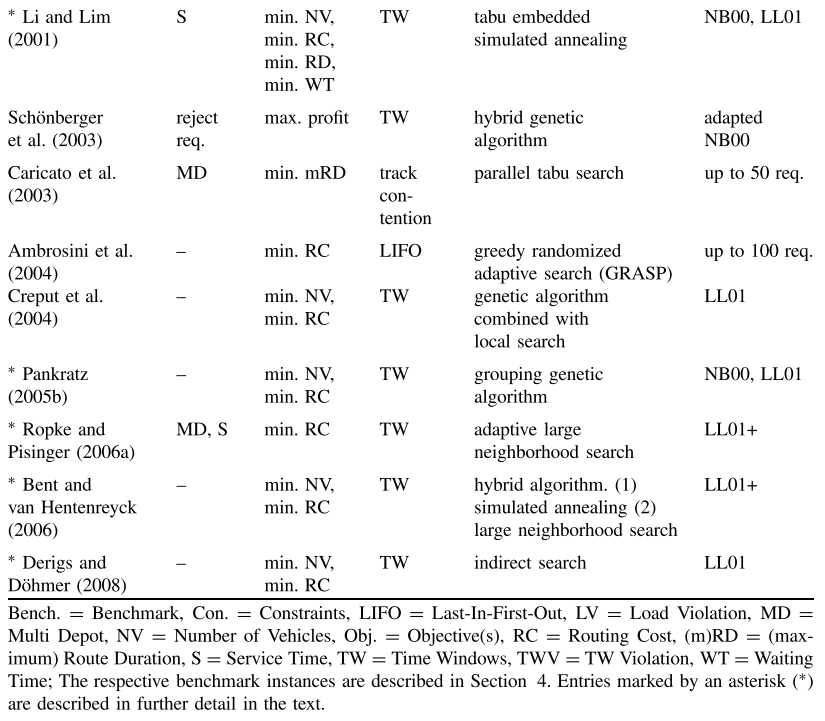
Carrabs等人（2007）讨论了SPDP扩展的可变邻域搜索。解决的问题包括关于后装的进一步限制，即物品只能以后进先出的方式交付。使用八种不同的构造技术生成初始解决方案。邻域由偶交换、块交换、重定位块、2-opt-L（2-opt仅考虑LIFO可行弧交换）和多重定位算子定义。

Li和Lim（2001）为PDP开发了一种禁忌嵌入模拟退火方法。定义了提货和交货对交换邻域。这些操作基于移位、交换和重新排列运算符。前两个定义了元启发式搜索的邻域，第三个用于优化后的目的。

Pankratz（2005b）提出了一种用于PDP的分组遗传算法。它与传统遗传算法的不同之处在于使用了面向组的遗传编码。Pankratz（2005b）使用的编码对应于形成路由的请求集群。编码中未包含的路由方面在解码染色体时添加.

Ropke和Pisinger（2006a）提出了一种适用于PDPTW的自适应大邻域搜索算法。多个仓库以及服务时间的存在可以通过手头的方法来处理。在Pisinger和Ropke（2007）以及Ropke和Pisinger（2006b）中，通过将VRP和VRPB实例转换为丰富的PDPTW，所提出的方法被用于解决VRP和VRTB实例。有关此解决程序的更多详细信息，请参阅本调查的第一部分。

Bent和van Hentenryck（2006）提出了静态PDPTW的两阶段混合算法。第一阶段使用模拟退火来减少所需的车辆数量。第二阶段包括大型邻域搜索算法，以降低总旅行成本。

Derings和D¨ohmer（2008）讨论了针对相同问题的间接（进化）局部搜索启发式方法。在间接搜索中，对解决方案进行编码，使确保可行性的问题与元启发式搜索过程分离。这里使用贪婪解码。

3.2.4 Summary

总之，用最先进的方法解决的最大静态PDP问题实例包括205个请求（Sigurd等人，2004）。然而，解决的最大实例的大小并不总是一个好的指标；严格约束的问题比不严格约束的更容易解决。最常用于评估静态PDPTW（元）启发式方法性能的基准数据集是Li和Lim（2001）中描述的数据集（LL01，LL01+，见表6）。Ropke和Pisinger（2006年a）以及Ben和van Hentenryck（2006年）这两个元启发式求解程序中给出了最新的最佳结果。Li和Lim（2001）的metaheuristic仍然对部分较小的实例保持最佳结果。然而，也提出了精确的方法；LL01数据集中约束更为严格的部分最近通过一种最先进的分支、切割和价格算法得到了解决（Ropke和Cordeau 2006）。

3.2.5 Related work

提货和交货问题不仅出现在车辆路线上，也出现在海运中。Christiansen和Nygreen（1998a）提出了一种结合PDPTW和多库存模型的船舶路径选择模型。它通过列生成来解决。Christiansen和Nygreen（1998b）以及Christiansen（1999）提出了类似的解决方案。Christiansen和Nygreen（2005年）也使用了列生成，假设航行时间不确定，并考虑到库存约束较软。Christiansen和Fagerholt（2002）报道了传统PDPTW在船舶路线中的另一种精确求解方法。Brønmo等人（2007）提出了一种多起点局部搜索启发式方法。Fager-holt（2001）提出了一种考虑到软时间窗的多船PDPTW的宽松版本。Fagerholt和Christiansen（2000a）研究了一个组合的船舶调度和分配问题。计算了几种实际情况的最优解。Fagerholt和Christiansen（2000b）研究了组合问题的子问题，即具有分配和优先约束的TSPTW。关于船舶路线问题的广泛调查，我们参考Christiansen等人（2004）。

Recker（1995）提出了PDPTW的一个有趣的扩展，即家庭活动模式问题。它包括共享车道和车辆切换选项。目标是尽量减少家庭旅行的不实用性。Recker用遗传算法解决了这个问题。

Dumitrescu（2005）对SPDP进行了多面体分析研究。讨论了新的有效不等式。L¨ubecke（2004）研究了组合简单的拾取和传送路径。这些是几个短模式的串联。每个模式包括访问最多两个请求。

Gambardella和Dorigo（2000）阐述了与PDP相关的另一个问题，即顺序排序问题。其目标是确定有向图中的最小权重哈密顿路径，在弧和顶点上具有权重，并重新检查顶点之间的优先约束。与PDPTW相反，一个ver-tex可以有多个前代。Gambardella和Dorigo（2000）提出了一种基于蚁群优化的方法来解决这个问题。其他解决方法包括，例如Escudero（1988）和Ascheuer等人（1993）的方法。

3.3 Dynamic and stochastic pickup and delivery problems

尽管许多真实世界的PDP本质上是动态的，但动态版本的PDP并没有像静态版本那样受到关注。术语“动态”通常表示请求的路由和调度必须实时完成；新的请求在规划期内动态出现，必须插入到现有的部分路由中。一般来说，采用与静态PDP相同的目标，即总运营成本最小化。Ghiani等人（2003年）和Psaraftis（1988年）对动态路线进行了调查。在PDP的随机变体中，关于数据的某一部分（例如车辆行驶时间）的信息仅在概率分布方面可用。到目前为止，还没有使用精确的程序来求解动态或随机PDP。在下文中，讨论了为PDP的动态和随机版本提出的不同启发式和元启发式方法

3.3.1 Heuristics

Swihart和Papstavrou（1999）求解随机SPDP。他们假设新的请求是按照泊松过程到达的；取件和交货地点统一分布在服务区域；并且单个车辆在欧几里得平面中以恒定速度行驶。最小化的目标是请求保留在系统中的预期时间。他们测试了三种路由策略：分区策略、最近邻居策略和堆垛机策略。堆垛机策略是指将到达的需求分组为大小相等的连续集合，并根据先到先得的原则为其提供服务。计算请求在轻流量和重流量条件下保留在系统中的预期时间的下限。

Ascheuer等人（2000）研究了单服务器PDP的三种在线算法（REPLAN、IGNORE和SMARTSTART）。考虑的目标是完成时间。在文献中，当前的问题被称为在线拨号问题。然而，拨号问题的使用方式与本调查中定义的不同。在线一词是指在事先不知道任何请求的情况下使用的。通过竞争分析，即将在线（不知道未来）算法与其离线（完全了解未来）算法进行比较（Van Hentenryck和Bent 2006；Jaillet和Stafford 2001），可以看出REPLAN和IGNORE具有5/2的竞争性，而SMARTSTART具有2的竞争性。Hauptmeier等人（2000）讨论了REPLAN和IGNORE在合理负载下的性能。Feuerstein和Stougie（2001）为同一问题设计了另一种2-竞争算法。Coja Oghlan等人（2005）研究了概率版本，Krumke等人（2005年）研究了最小化最大流量时间的在线问题。

Savelsbergh和Sol（1998）提出了动态多车辆PDP的第一个启发式方法。他们的解决方法称为DRIVE（独立车辆的动态路由），结合了基于集合划分问题公式的分支和价格算法。它通过不完全优化生成近似解。解决的问题是十天的真实生活模拟。在各种重新优化运行中，最多可考虑354个活动请求。

Lipmann等人（2004）研究了受限信息对多服务器在线PDP的影响，即请求的目的地仅在对象被拾取后才被显示。Yi和Tian（2005）计算了时间窗情况下两种确定性策略（REPLAN和SMARTCHOICE）的竞争比率.

Popken（2006）讨论了动态多车辆PDP的基于插入的启发式方法。它与不同类型的顺序电路控制相结合，以提高车辆容量的有效利用率。报告多达2500个初始订单的测试实例的结果。

Fabri和Recht（2006）提出了一种启发式算法对dy的适应性-动态PDPTW。Caramia等人（2002）最初为动态DARP设计。与Caramia等人相反，他们允许车辆等待时间。为了增强该过程，引入了附加的局部搜索阶段。此阶段在插入新请求时开始，在下一个请求到来时结束。Fabri和Recht（2006）报告了最多1000个请求的实例的解决方案，平均每分钟一个请求.

Thangiah和Awan（2006）也在实时环境中测试了他们的算法（见表2），考虑了多达159个请求。

3.3.2 Metaheuristics

Jih和Hsu（1999）提出了一种基于种群的元启发式方法，即混合遗传算法，用于具有TW的动态SPDP。它被称为混合算法，因为遗传算法与动态规划算法相结合。用于测试的数据集最多包含50个请求。

Shen等人（1995）对动态多车辆PDP进行了早期研究和Potvin等人（1995）。这两篇文章都侧重于具有实时支持车辆调度员的学习能力的神经网络。在Potvin等人（1995）中，将基于神经网络的学习技术与基于线性规划的方法进行了比较。Potvin等人（1995）和Shen等人（1995年）分别使用具有200和140个请求的真实数据集来评估其算法的性能。Potvin等人（1995）得出结论，神经网络比线性规划模型表现更好。

Malca和Semet（2004）提出了动态多车辆PDPTW的第一种基于邻域的元启发式求解方法。所使用的邻域属于请求到车辆分配类型。为了加速搜索，使用了消除矩阵。它存储两个请求的兼容性。因此，只考虑有希望的行动。在Li和Lim（2001）的一些改编实例上测试了拟议程.

Mitrovi´c-Mini´c和Laporte（2004）描述了动态PDPTW的两阶段解决程序。在第一阶段，通过最便宜的插入构建初始解决方案。该解决方案通过禁忌搜索算法进行了改进。在第二阶段，使用不同的等待策略来调度请求。尝试的等待策略被称为驱动优先、等待优先、动态等待和高级动态等待。当等待发生时，他们对车辆的位置有所不同。在驾驶优先策略中，车辆尽早离开每个顶点。如果它在下一站到达得太早，它会在那里等待，直到服务可行。使用等待优先策略时，车辆将尽可能晚地离开每个顶点，并考虑后续顶点的时间窗口。动态等待是指根据时间窗口将客户聚集在一起的策略。车辆在转向下一个集群的第一个客户之前，应尽可能长时间等待。高级动态等待表示一种策略，其中访问第一个集群之前的等待时间取决于在最后一个集群开始服务的最新可能时间，而不违反中间集群的时间窗口。Mitrovi´c-Mini´c和Laporte（2004）报告了针对问题实例的解决方案，总共有1000个请求，这些请求都发生在服务期间。结果表明，先进的动态等待策略是最有效的.

Mitrovi´c-Mini´c等人（2004）也使用了高级动态等待基于地平线的启发式。路由部分通过禁忌搜索改进的构造方法来解决。根据高级动态等待进行调度。管线被分段。第一段对应于短期水平线，路线的剩余部分对应于长期水平线。还考虑了几个仓库的情况。再次解决了总数高达1000个请求的实例。

Gutenschwager等人（2004）比较了最速下降、反应禁忌搜索和模拟退火算法。他们解决了电动单轨系统上的动态PDP。用禁忌搜索算法得到了最佳结果。

在Pankratz（2005a）中，将静态PDP的分组遗传算法嵌入滚动水平框架中，以解决动态PDPTW。它在具有不同动态程度的数据集上进行了测试。

提出了一种动态多车PDPTW的禁忌搜索算法-由Gendreau等人（2006）提出。它使用了一个弹出链邻域（Glover 1996），即一个请求从其当前路径中删除，并插入到另一个路径中，强制将该路径上的请求弹出到第三个路径，依此类推。目标函数中包含了一个迟到标准。为了加快优化过程，进行了并行实现。所得到的程序在7.5小时内进行了模拟测试，每小时20辆车和23个请求，在4小时内进行10辆车和33个请求.

3.3.3 Summary

总之，在过去几十年中，在动态PDP领域，已经开发了许多解决方案。然而，所提出的算法无法直接比较，因为到目前为止，没有一组以上的作者使用过标准化的模拟环境。基准实例可用；e、 g.Mitrovi´c-Mini´c和Laporte（2004）以及Mitrovi‘c-Mini’c等人（2004）中使用的那些，见第4节。

3.4 The static dial-a-ride problem

3.4.1 Exact methods

3.4.2 Heuristics

3.4.3 Metaheuristics

3.4.4 Summary

3.4.5 Related work

3.5 Dynamic dial-a-ride problems

3.5.1 Exact methods

3.5.2 Heuristics

3.5.3 Metaheuristics

3.5.4 Summary

4 Benchmark Instances for VRPPD

表6为感兴趣的读者提供了文献中使用的可用基准实例的信息。第一列提供了文献参考。第二列到第四列说明了问题类型、不同实例的大小（按每个实例的请求数）以及提供的实例数。然后，对数据集以及本文中使用的缩写进行了简要描述。

主要用于评估PDPTW绩效的数据集是Li和Lim（2001）提出的数据集。Ropke和Pisinger（2006年a）以及Bent和van Hentenryck（2006年）提供了主要数据集和扩展数据集的最新最佳结果。

与PDP领域相反，为DARP开发的解决方案方法尚未在标准化基准实例上进行测试。这可能是由于大多数方法在考虑的约束条件以及最小化的目标方面存在很大差异。然而，由于现在确实存在相当标准的问题设置数据集，这可能会在不久的将来发生变化。

5 Conclusion

本文提出的解决方法是VRPPD领域的最新技术。根据本调查的第一部分，我们认为，未来的研究将包括更多的现实生活约束、动态的影响以及关于未来事件的知识，以概率分布的方式。此外，与许多其他路由问题相比，DARP是一个自然的多目标问题。这方面也将是未来调查的一部分。
我们希望并相信，这项调查将有助于未来在涉及取车和交付的车辆路线领域进行研究

---