有意向获取代码，请转文末观看代码获取方式~也可转原文链接获取~

1 基本定义

MVMD信号分解+FFT+HHT组合算法是一种强大的分析方法，结合了变分模态分解(MVMD)、快速傅里叶变换(FFT)和希尔伯特-黄变换(HHT)。

首先，使用MVMD将原始信号分解成多个IMF（本征模态函数），然后对每个IMF进行FFT计算其频谱，最后使用HHT分析其时频特征。这种组合方法可以综合利用三种方法的优点，对于处理非线性和非平稳信号具有较高的准确性和鲁棒性。

其中，MVMD是一种用于处理非线性和非平稳信号的自适应信号分解方法，通过在信号中加入白噪声，并多次进行经验模态分解，从而获得原信号的多种本征模态函数。这些IMF可以更好地捕捉到信号中的局部特征，特别是对于非线性、非平稳信号。

FFT是一种高效的计算离散傅里叶变换(DFT)和其逆变换的算法，可以在短时间内计算出信号在频域上的表达，从而提供信号的频率特征。

HHT是一种用于分析非线性和非平稳信号的数学工具，通过将信号分解成一系列固有模态函数(IMF)，并计算每个IMF的瞬时频率，从而提供信号的时频特征。

这种组合方法在处理复杂的非线性、非平稳信号时具有独特的优势。首先，MVMD能够自适应地将信号分解成多个本征模态函数，这些IMF可以更好地捕捉到信号中的局部特征，特别是对于非线性、非平稳信号。其次，FFT可以计算出每个IMF的频谱，提供信号的频率特征，这对于分析信号的周期性和频域特征非常重要。最后，HHT可以提供信号的时频特征，对于分析信号的瞬时频率和时变特性非常有用。

需要注意的是，这种组合方法也存在一些局限性。例如，MVMD和HHT都存在端点效应问题，即在进行信号分解和分析时，需要考虑信号的边界条件。此外，这种组合方法需要使用大量的计算资源，特别是在处理大规模数据时，需要进行多次FFT和HHT计算。因此，在实际应用中需要根据具体的问题和数据特点进行选择和优化。

除了上述提到的优点，这种组合方法还有一些其他的优点。

首先，MVMD和HHT都具有自适应性，可以自适应地适应信号的特征，从而更好地捕捉到信号中的局部特征和时变特性。这种自适应性使得这两种方法在处理非线性和非平稳信号时具有较高的准确性和鲁棒性。

其次，FFT作为一种经典的频域分析方法，可以提供信号的频率特征，这对于分析信号的周期性和频域特征非常重要。通过将MVMD和FFT结合起来，可以同时获得信号的时域和频域特征，从而更全面地了解信号的性质。

最后，这种组合方法可以用于处理多维信号和数据。例如，可以在MVMD阶段将多维信号分解成多个IMF，然后在FFT和HHT阶段分别计算每个IMF的频谱和时频特征。这样可以对多维信号进行全面的分析和处理，提供更丰富的信息。

然而，这种组合方法也存在一些局限性。首先，MVMD和HHT都存在端点效应问题，即在进行信号分解和分析时，需要考虑信号的边界条件。这可能会限制这两种方法在处理实际信号时的适用性。其次，这种组合方法需要使用大量的计算资源，特别是在处理大规模数据时，需要进行多次FFT和HHT计算。因此，在实际应用中需要根据具体的问题和数据特点进行选择和优化。

2 出图效果

附出图效果如下：

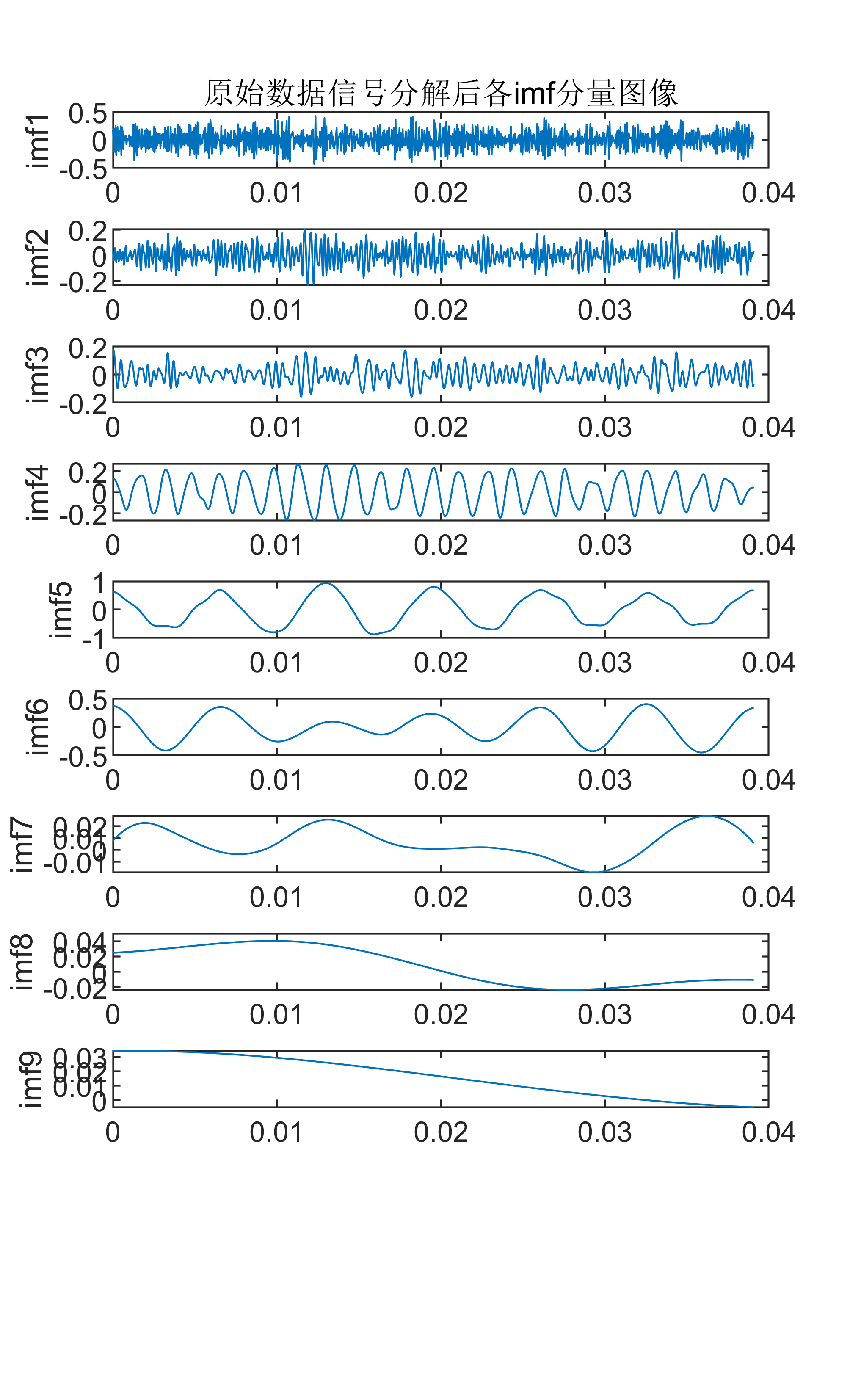
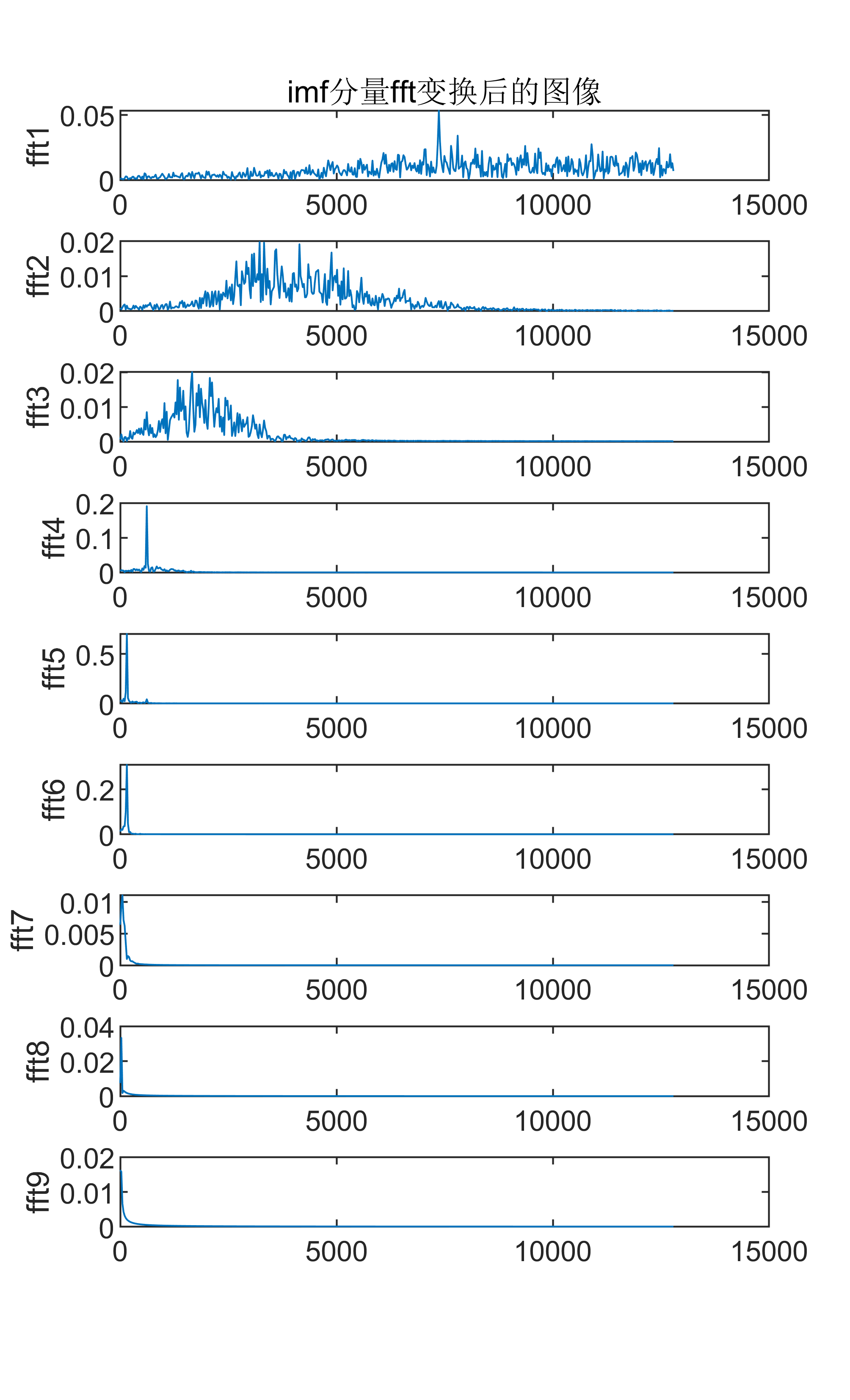
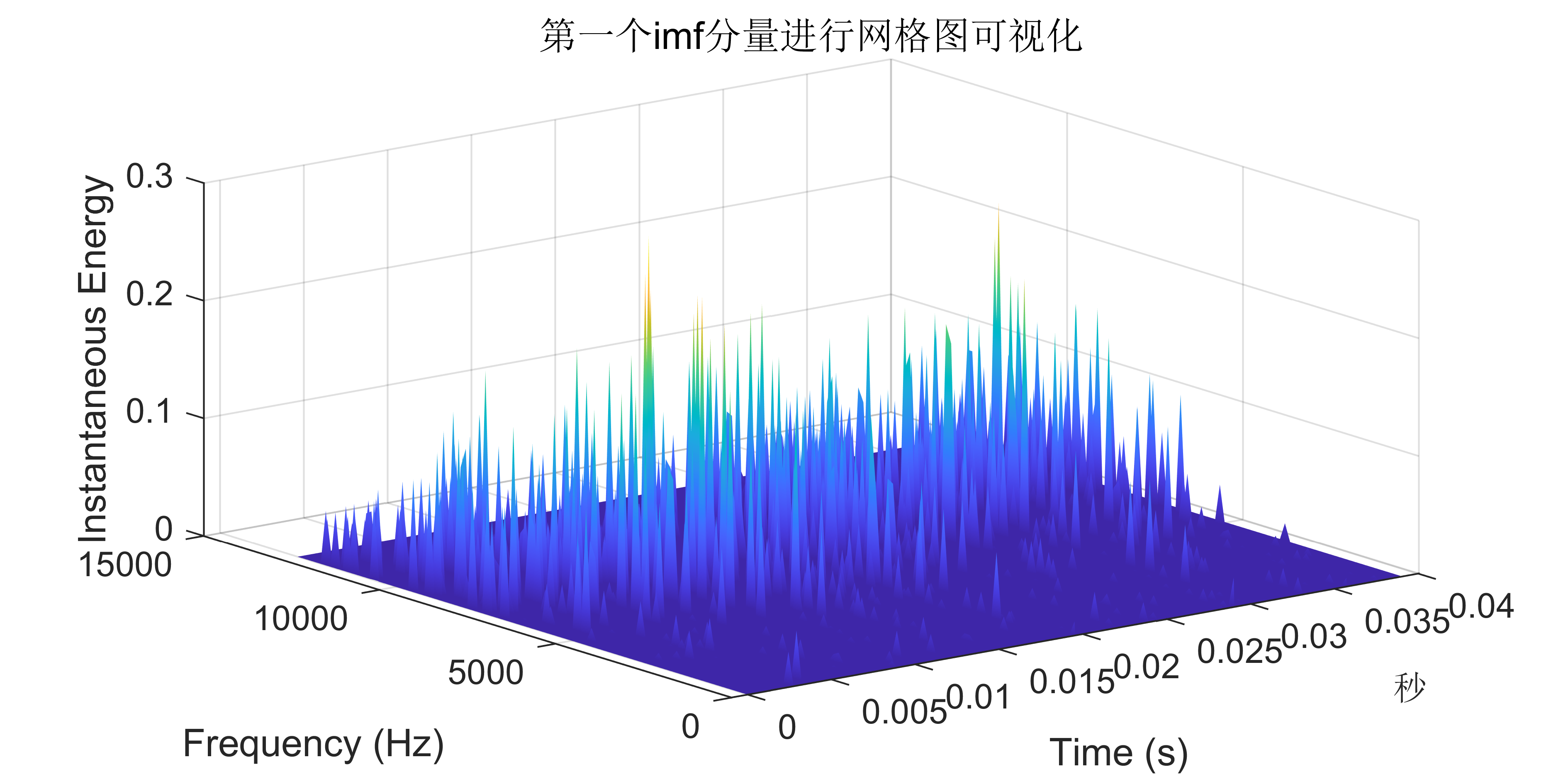
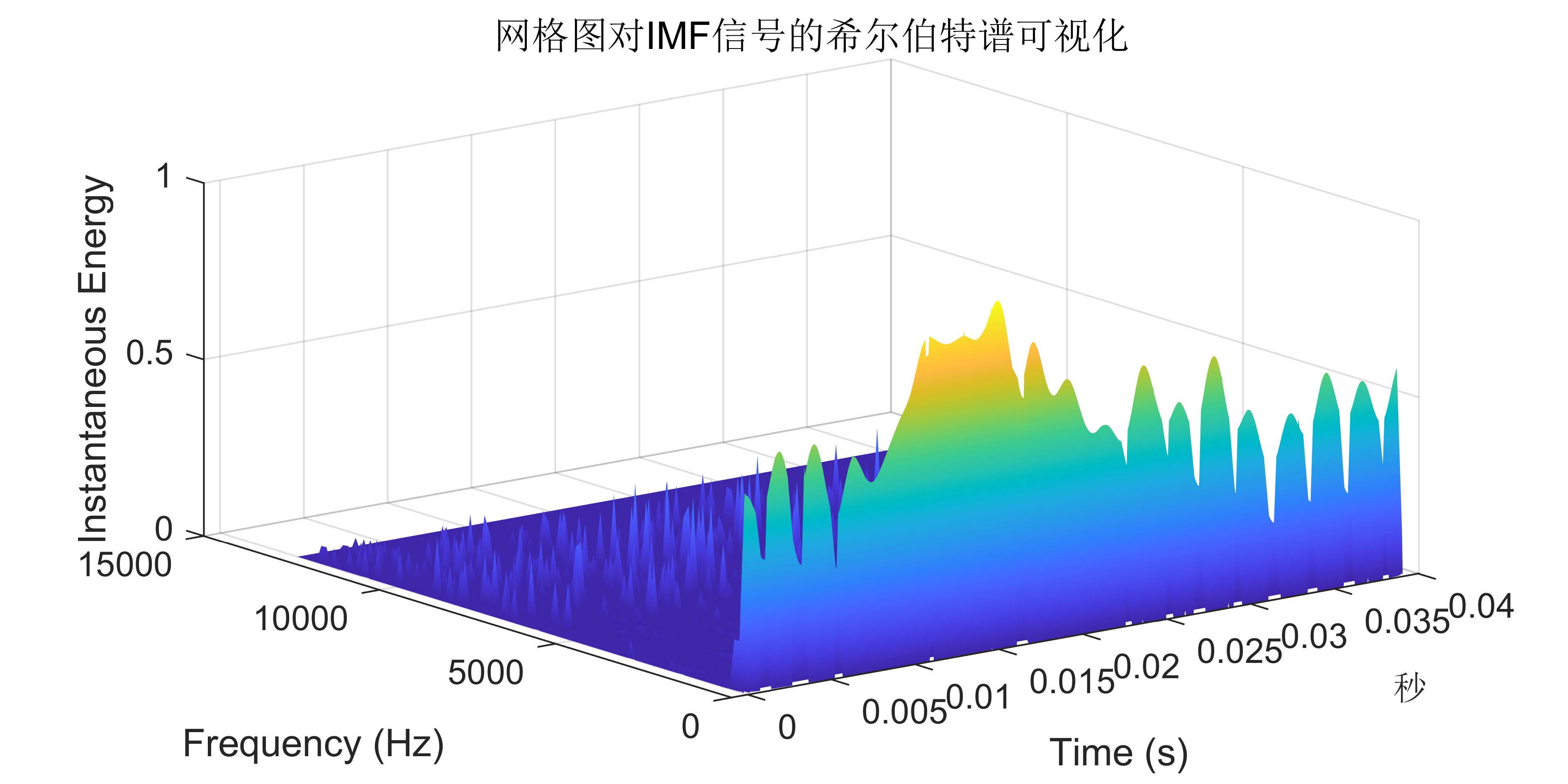
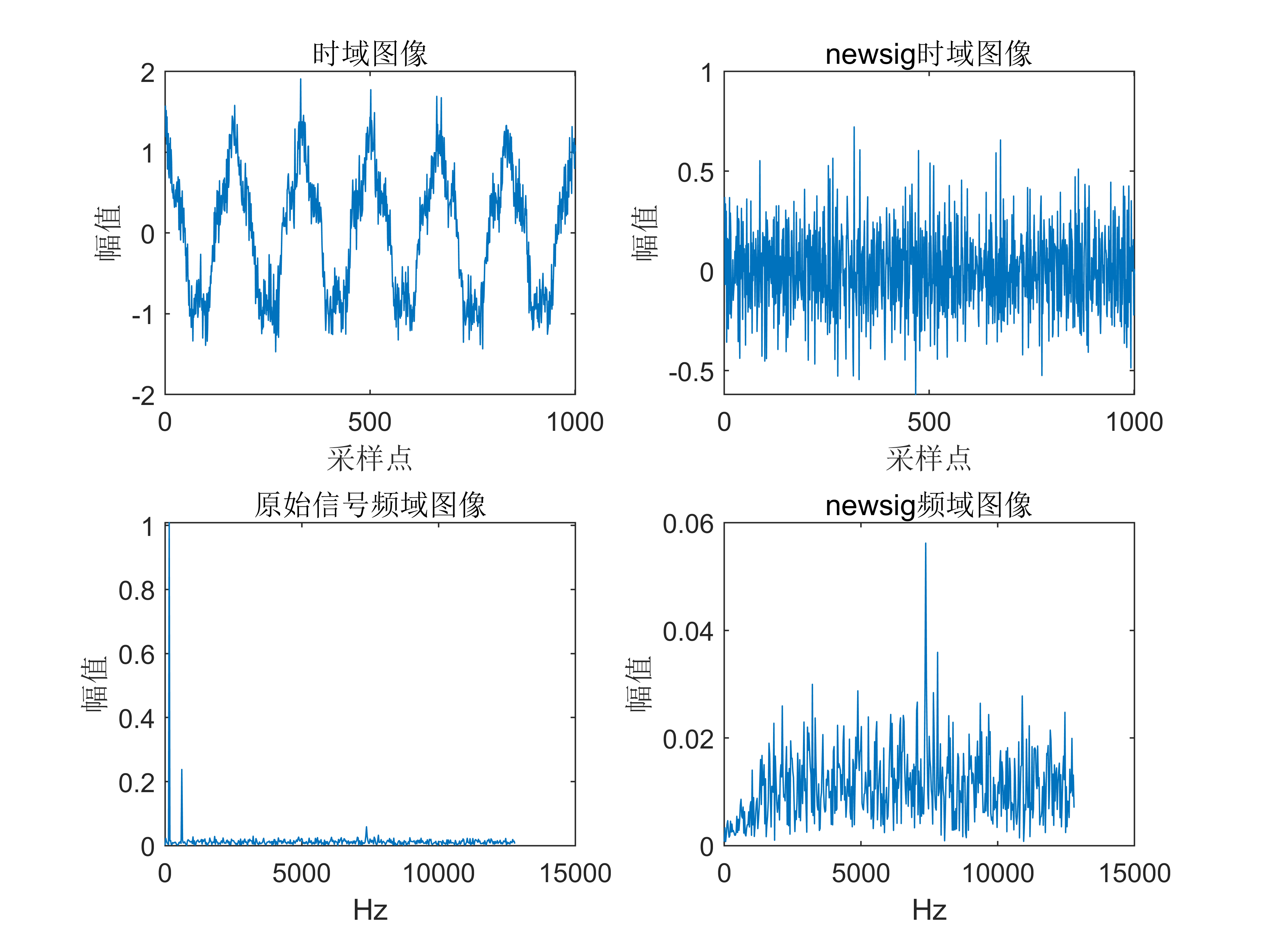
附视频教程操作：