目录
- 引言
- 一、高精度加法
- 1.题目描述
- 2.代码实现
- 3.测试
- 二、高精度减法
- 1.题目描述
- 2.代码实现
- 3.测试
- 三、高精度乘法
- 1.题目描述
- 2.代码实现
- 3.测试
- 四、高精度除法
- 1.题目描述
- 2.代码实现
- 3.测试
引言
本文介绍了高精度加法、高精度减法、高精度乘法、高精度除法,这个高精度来说还是有点用的,在一些竞赛啥的还是能用得上的,当然了这个只针对C++来说,java或者python本身就有大整数类型,没必要搞这个。
一、高精度加法
当然先说一下什么是高精度,就是一个很长的数,拿long long也存不下的这种,虽然long long很大有9.2*10^18那么大,可是长度也就19而已,所以要是我输入一个长度50或者100的数,就没有办法了,所以这就是高精度存在的意义,然后思想就是拿string来存,然后根据一些运算特性每一位每一位的处理,然后整合就是最终结果了。
1.题目描述
给定两个正整数(不含前导 0),计算它们的和。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的和。
数据范围:1≤整数长度≤100000
输入样例:
12
23
输出样例:
35
2.代码实现
说一下思路啊,首先是输入的问题,因为要加法,肯定是从个位加的,然后需要进位,所以肯定个位是从0号下标开始好,因为如果从size-1号下标遍历也行,只不过如果牵扯到进位的话,那么就得从头插了,那就需要特判还要移动整个数组就太费劲了,所以选择把个位存到0号下标去。
然后是加法的问题了,首先定义一个t代表进位,然后从个位开始循环每一位,因为不知道A和B谁长所以循环条件这样写,然后t也可能最后也有进位所以也加入判断条件了,因为最后i可能会超出A或者B的范围,所以在循环里还要判断一下才能加,然后t % 10存到C中,t /= 10,就完成了一次操作,最后要把前导0给去掉,最后从后向前输出C就行了。
#include <iostream>
#include <vector>
using namespace std;
vector<int> add(vector<int> &A, vector<int> &B)
{
vector<int> C;
int t = 0;
for(int i = 0; i < A.size() || i < B.size() || t; ++i)
{
if(i < A.size()) t += A[i];
if(i < B.size()) t += B[i];
C.push_back(t % 10);
t /= 10;
}
return C;
}
int main()
{
string a, b;
cin >> a >> b;
vector<int> A, B;
for(int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; --i) B.push_back(b[i] - '0');
auto C = add(A, B);
for(int i = C.size() - 1; i >= 0; --i) printf("%d", C[i]);
return 0;
}
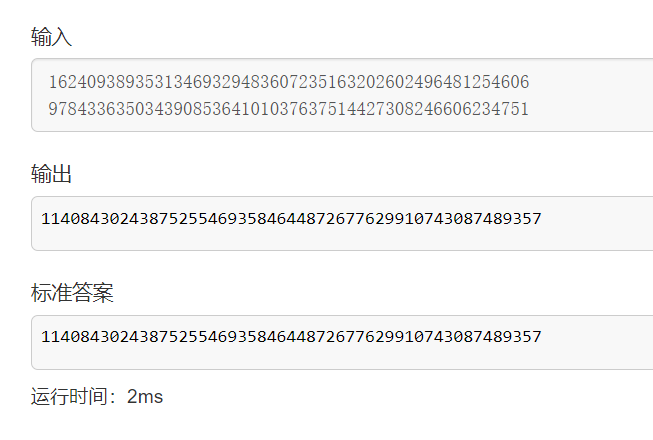
3.测试
可以看出是完全正确的,也AC了


二、高精度减法
1.题目描述
给定两个正整数(不含前导 0),计算它们的差,计算结果可能为负数。
输入格式
共两行,每行包含一个整数。
输出格式
共一行,包含所求的差。
数据范围
1≤整数长度≤105
输入样例:
32
11
输出样例:
21
2.代码实现
这个减法其实跟加法差不多,区别在于,如果是负数,还是大的减去小的,只不过前面要添个’-',其余的问题看代码或者注释问题都不太大了
#include <iostream>
#include <vector>
using namespace std;
bool cmp(string a, string b) //a >= b ?
{
if(a.size() != b.size()) return a.size() > b.size();
for(int i = 0; i < a.size(); ++i)
{
if(a[i] != b[i]) return a[i] > b[i];
}
return true;
}
vector<int> sub(vector<int> &a, vector<int> &b)
{
vector<int> C;
int t = 0;
for(int i = 0; i < a.size(); ++i)
{
t += a[i];
if(i < b.size()) t -= b[i]; //因为b是小于a的
C.push_back((t + 10) % 10); //t可能大于0,也可能小于0,这样做全包括了
if(t < 0) t = -1;
else t = 0;
}
while(C.size() > 1 && C.back() == 0) C.pop_back(); //可能存在前导0
return C;
}
int main()
{
string a, b;
cin >> a >> b;
bool sign = cmp(a,b);
if(!sign)
{
printf("-");
swap(a,b);
}
vector<int> A, B;
for(int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
for(int i = b.size() - 1; i >= 0; --i) B.push_back(b[i] - '0');
auto C = sub(A,B);
for(int i = C.size() - 1; i >= 0; --i) printf("%d", C[i]);
return 0;
}
3.测试
可以看出都是正确的,然后最后也AC了

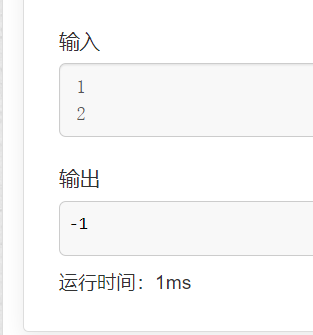


三、高精度乘法
1.题目描述
给定两个非负整数(不含前导 0) A 和 B,请你计算 A×B 的值。
输入格式共两行,第一行包含整数 A,第二行包含整数 B。输出格式共一行,包含 A×B 的值。
数据范围
1≤A的长度≤100000,0≤B≤10000
输入样例:
2
3
输出样例:
6
2.代码实现
这个高精度乘法正常的算不太一样,这是从高精度的每一位算起,每一位都乘以这个小整数
#include <iostream>
#include <vector>
using namespace std;
vector<int> mul(vector<int> &a, int b)
{
vector<int> C;
int t = 0;
for(int i = 0; i < a.size() || t; ++i)
{
if(i < a.size()) t += a[i] * b;
C.push_back(t % 10);
t /= 10;
}
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
auto C = mul(A,b);
for(int i = C.size() - 1; i >= 0; --i) printf("%d", C[i]);
return 0;
}
3.测试
可以看出结果都是正确的,这道题也AC了


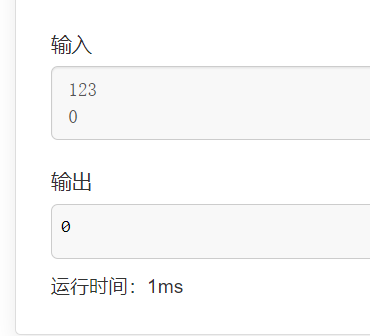

四、高精度除法
1.题目描述
给定两个非负整数(不含前导 0) A,B,请你计算 A/B 的商和余数。
输入格式共两行,第一行包含整数 A,第二行包含整数 B。输出格式共两行,第一行输出所求的商,第二行输出所求余数。
数据范围1≤A的长度≤100000,1≤B≤10000 ,B 一定不为 0
输入样例:
7
2
输出样例:
3
1
2.代码实现
这里注意一下的是,这个除法是从高位算起的,但因为正常情况下给出的a个位都是0下标,然后输出也因为是个位为0下标,因为输入输出的原因所以div就处理的多了一些,不过核心还是不变的
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
vector<int> div(vector<int> &a, int b, int &r)
{
vector<int> C;
r = 0;
for(int i = a.size() - 1; i >= 0; --i)
{
r = r * 10 + a[i];
C.push_back(r / b);
r %= b;
}
reverse(C.begin(), C.end());
while(C.size() > 1 && C.back() == 0) C.pop_back();
return C;
}
int main()
{
string a;
int b;
cin >> a >> b;
vector<int> A;
for(int i = a.size() - 1; i >= 0; --i) A.push_back(a[i] - '0');
int r; //余数
auto C = div(A, b, r);
for(int i = C.size() - 1; i >= 0; --i) printf("%d", C[i]);
printf("\n%d", r);
return 0;
}
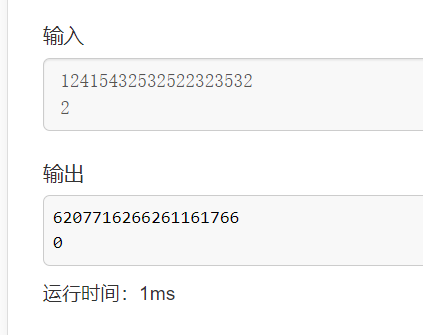
3.测试
可以看出来也是没问题的