一,最长回文串
1.题目
给你一个字符串
s,找出其中最长的回文子序列,并返回该序列的长度。子序列定义为:不改变剩余字符顺序的情况下,删除某些字符或者不删除任何字符形成的一个序列。
示例 1:
输入:s = "bbbab" 输出:4 解释:一个可能的最长回文子序列为 "bbbb" 。示例 2:
输入:s = "cbbd" 输出:2 解释:一个可能的最长回文子序列为 "bb" 。提示:
1 <= s.length <= 1000s仅由小写英文字母组成
2.题目接口
class Solution {
public:
int longestPalindromeSubseq(string s) {
}
};3.解题思路及其代码
在思考这道题时,我们先想到的可能是dp[i]来作状态转移方程,表示以第i个位置为结尾的最长回文子序列。但是,我们是不能这样定义的。因为第i个位置能不能加入到这个子序列中是要看当前子序列的开头位置的字符是否与之匹配的。
在弄明白抛弃掉这种想法以后,我们便可以试着以区间dp的方式来解决:
1.状态表示:dp[i][j],表示在区间[i,j]的最长子序列。
2.状态转移方程:对于状态转移方程的推导需要分类讨论,分类如下:
在第二种情况下dp[i][j]要等于在这三种情况下的最大值,又因为dp[i+1][j-1]其实是在剩下的两种情况中包含的,所以dp[i][j] = max(dp[i+1][j],dp[i][j-1])。
代码:
根据以上思路写出代码如下:
class Solution { public: int longestPalindromeSubseq(string s) { int n = s.size(); vector<vector<int>>dp(n,vector<int>(n)); for(int i = n-1;i>=0;i--)//因为有dp[i][j] = dp[i+1][j]的情况,所以要从下到上初始化 { for(int j = i;j<n;j++)//j>=i { if(s[i] == s[j])//第一种情况 { if(j>i) dp[i][j] = dp[i+1][j-1]+2;//j>i才能加2 else dp[i][j] = 1;//i == j,个数为1 } else//第二种情况 { dp[i][j] = max(dp[i+1][j],dp[i][j-1]);//不用担心越界的情况,因为当j == 0时 //i一定等于0,所以会在第一种情况中处理 } } } return dp[0][n-1]; } };
二,让字符串成为回文串的最小插入次数
1,题目
1312. 让字符串成为回文串的最少插入次数
提示
困难
218
相关企业
给你一个字符串
s,每一次操作你都可以在字符串的任意位置插入任意字符。请你返回让
s成为回文串的 最少操作次数 。「回文串」是正读和反读都相同的字符串。
示例 1:
输入:s = "zzazz" 输出:0 解释:字符串 "zzazz" 已经是回文串了,所以不需要做任何插入操作。示例 2:
输入:s = "mbadm" 输出:2 解释:字符串可变为 "mbdadbm" 或者 "mdbabdm" 。示例 3:
输入:s = "leetcode" 输出:5 解释:插入 5 个字符后字符串变为 "leetcodocteel" 。提示:
1 <= s.length <= 500s中所有字符都是小写字母。
2.题目接口
class Solution {
public:
int minInsertions(string s) {
}
};3.解题思路及其代码
对于这种回文串问题,因为有了上面的定义状态表示的经验所以还是使用一个二维的dp表解决问题。
1.状态表示:dp[i][j]表示在[i,j]这个区间内使这个区间内的字符串成为回文串的最小插入次数。
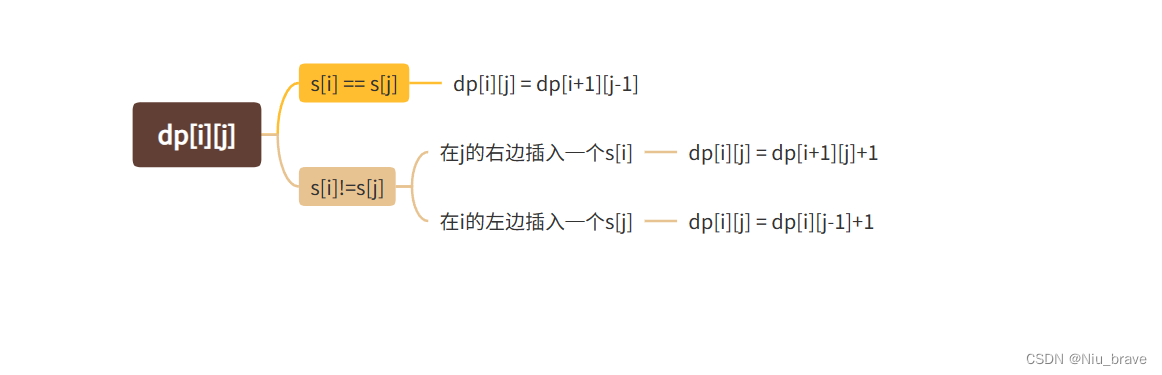
2.状态转移方程:在这里状态转移方程还是要分类讨论,还是要看s[i],s[j]是否相等:
在第二种情况下要取两者的较小值。
代码:
由以上思路写出代码如下:
class Solution { public: int minInsertions(string s) { int n = s.size(); vector<vector<int>>dp(n,vector<int>(n)); for(int i = n-1;i>=0;i--)//有dp[i][j] = dp[i+1][j]+1的情况,所以要从下到上遍历 { for(int j = i;j<n;j++) { if(s[i] == s[j]) { if(j>i) dp[i][j] = dp[i+1][j-1];//只有一个字符不用搞了 } else { dp[i][j] = min(dp[i+1][j],dp[i][j-1])+1; } } } return dp[0][n-1]; } };