一、说明
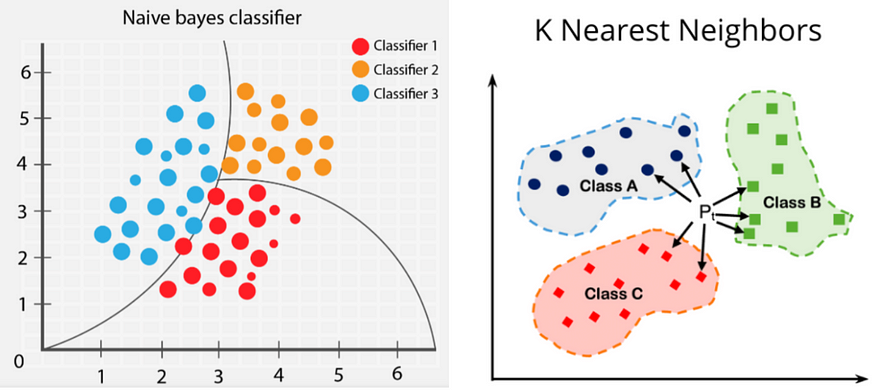
在在这篇文章中,我将解释两种机器学习算法,称为贝叶斯定理和 K 最近邻算法。贝叶斯定理以 18 世纪英国数学家托马斯·贝叶斯的名字命名,是确定条件概率的数学公式。k 最近邻算法,也称为 KNN 或 k-NN,是一种非参数监督学习分类器,它使用邻近性对单个数据点的分组进行分类或预测。
二、贝叶斯定理
2.1 设计一个掷色子的案例
示例 1:我有一个掷骰子的实验。
我有哪些要素:
{1,2,3,4,5,6}
Probability if 1 coming when I roll a dice?
P(1) = 1/6
Probability if 2 coming when I roll a dice?
P(2) = 1/6
Probability if 3 coming when I roll a dice?
P(3) = 1/6
Probability if 4 coming when I roll a dice?
P(4) = 1/6
Probability if 5 coming when I roll a dice?
P(5) = 1/6
Probability if 6 coming when I roll a dice?
P(6) = 1/6这些事件基本上称为独立事件。因为获得一种元素的概率不依赖于其他元素。
2.2 再来一个弹球案例
示例 2:我有一盒弹珠。
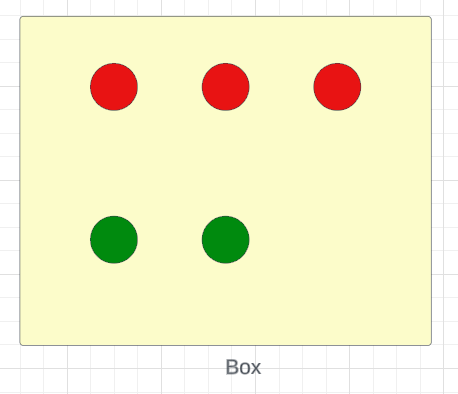
//Probability of taking out a red Marble and you remove it from the Box
P(R) = 3/5
//Now Probability of taking out a green Marble
P(R) = 2/4 = 1/2这些事件是相关事件,因为当您从盒子中取出弹珠时,弹珠的数量会减少。
//Now what is the Probability of taking out a red Marble and then a green Marble
//We can denote it by
P(R) * P(G/R) : This P(G/R) is called as conditional probability. This means Probability of Green when given Red
P(A and B) = P(A) * P(B/A)P(A 和 B) 是否等于 P(B 和 A)?是的
P(A and B) = P(A) * P(B/A) -> 1
P(B and A) = P(B) * P(A/B) -> 2
//Let's explain this using our Marble Box example,
R = Red Marble G = Green Marble
{R, R, R, G, G}
P(B and G) = P(R) * P(G/R) = 3/5 * 2/4 = 3/ 10
P(G and B) = P(G) * P(R/G) = 2/5 * 3/4 = 3/ 10
//Now you can see both are equal.
Then:
P(A and B) = P(B and A) 现在我可以这样写这个方程:
P(A and B) = P(B) * P(A/B)
P(A) * P(B/A) = P(B) * P(A/B)
P(B/A) = P(B) * P(A/B) / P(A) : This is called as Bayes Theorem2.3 我们如何使用贝叶斯定理来解决问题?
假设我有一些特征(独立特征),如x1、x2、x3、x4,我的输出是 Y(输出特征),分别是yes 和 no。
现在,根据输入值,我需要使用贝叶斯定理预测输出。
//Probability of getting yes when given x1, x2, x3, x4 values can be shown as,
P(Y=yes/Given x1, x2, x3, x4) = P(Y=yes) * P(x1, x2, x3, x4 / Y=yes) / P(x1, x2, x3, x4…. xn)
//This can be wriiten like this,
P(Y=yes/x1, x2, x3, x4) = P(Y=yes) * P(x1/Y=yes) * P(x2/Y=yes) * P(x3/Y=yes) * P(x4/Y=yes) / P(x1) * P(x2) * P(x3) * P(x4)
//Probability of getting no when given x1, x2, x3, x4 values can be shown as,
P(Y=no/x1, x2, x3, x4) = P(Y=no) * P(x1/Y=no) * P(x2/Y=no) * P(x3/Y=no) * P(x4/Y=no) / P(x1) * P(x2) * P(x3) * P(x4)在这里您可以看到分母是固定的(对于是和否,您将获得相同的分母值)。这样我们就可以忽略分母。假设 P(Y=是/x1, x2, x3, x4) = 0.15 且 P(Y=否/x1, x2, x3, x4) = 0.05。在二元分类中,任何值 ≥ 0.5我们可以将其视为1,对于 ≤ 0.5我们可以将其视为0。
P(Y=yes/x1, x2, x3, x4) = 0.15
P(Y=no/x1, x2, x3, x4) = 0.05
// We do normalization to map this problem to Binary Classification. In the normalization we devide
the probability of actual value using sum of all the probabilities of actual values.
// After Nomalization :
P(Y=yes/x1, x2, x3, x4) = 0.15 / 0.15 + 0.05 = 0.15 / 0.20 = 0.75 which is > 0.5
P(Y=no/x1, x2, x3, x4) = 0.05 / 0.15 + 0.05 = 0.05 / 0.20 = 0.25 which is < 0.5让我们获取一个数据集并计算概率,这是关于在给定 4 个特征展望、温度、湿度和刮风条件时打高尔夫球的概率。

通过Outlook功能,我可以列出所有可能性并预测我们是否可以打高尔夫球。

我们可以打高尔夫球的概率 = 9 / (9 + 5) = 9 /14
我们不能打高尔夫球的概率 = 5 / (9 + 5) = 5 /14
根据温度功能,我可以列出所有可能性并预测我们是否可以打高尔夫球。
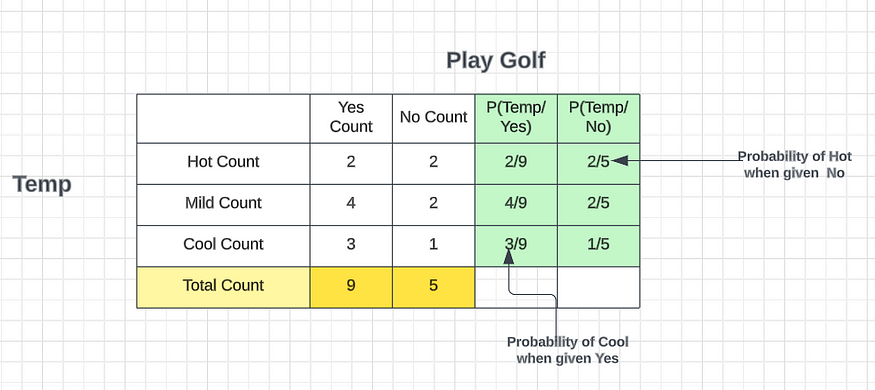
我们可以打高尔夫球的概率 = 9 / (9 + 5) = 9 /14
我们不能打高尔夫球的概率 = 5 / (9 + 5) = 5 /14
假设您获得新的测试数据,并获得Sunny 和 Hot作为数据,输出是什么?我们将使用贝叶斯定理尝试找到它。
P(是的/鉴于阳光明媚且炎热)?
P(Yes/ Given Sunny and Hot) = P(Yes) * P(Sunny / Yes) * P(Hot / Yes)
---------------------------------------
P(Sunny) * P(Hot)
Now you know that P(Sunny) * P(Hot) is a constant (For no also you will get the same value)
P(Yes/ Given Sunny and Hot) = P(Yes) * P(Sunny / Yes) * P(Hot / Yes)
P(Yes/ Given Sunny and Hot) = 9/14 * 3/9 * 2/9
= 6 / 14 * 9 = 2 / 24 = 1/ 21 = 0.0476
P(No/ Given Sunny and Hot) = P(No) * P(Sunny / No) * P(Hot / No)
---------------------------------------
P(Sunny) * P(Hot)
P(No/ Given Sunny and Hot) = P(No) * P(Sunny / No) * P(Hot / No)
= 5 /14 * 2/5 * 2/5 = 2 /35 = 0.057
P(Yes/ Given Sunny and Hot) = 0.0476
P(No/ Given Sunny and Hot) = 0.057
Nomalize the values
---------------------
P(Yes/ Given Sunny and Hot) = 0.0476 / 0.0476 + 0.057 = 0.0476 / 0.1046 = 0.45
P(No/ Given Sunny and Hot) = 0.057 / 0.0476 + 0.057 = 0.057 / 0.1046 = 0.545
So now you can see the posibility of No is > than 0.5 which is the Answer.
If the weather is Sunny and Hot what will the person do -> He should not play Golf 假设您获得了新的测试数据,并且获得了Rainy 和 Cool作为数据,输出是什么?我们将使用贝叶斯定理尝试找到它。
P(是的/考虑到下雨且凉爽)?
P(Yes/ Given Rainy and Cool) = P(Yes) * P(Rainy/ Yes) * P(Cool/ Yes)
---------------------------------------
P(Rainy) * P(Cool)
Now you know that P(Rainy) * P(Cool) is a constant (For probability no also you will get the same value)
P(Yes/ Given Rainy and Cool) = P(Yes) * P(Rainy / Yes) * P(Cool/ Yes)
P(Yes/ Given Rainy and Cool) = 9/14 * 2/9 * 3/9
= 1/21 = 0.048
P(No/ Given Rainy and Cool) = P(No) * P(Sunny / No) * P(Hot / No)
---------------------------------------
P(Sunny) * P(Hot)
P(No/ Given Rainy and Cool) = P(No) * P(Sunny / No) * P(Hot / No)
= 5 /14 * 3/5 * 1/5 = 3/70 = 0.043
P(Yes/ Given Rainy and Cool) = 0.048
P(No/ Given Rainy and Cool) = 0.043
Nomalize the values
---------------------
P(Yes/ Given Rainy and Cool) = 0.048 / 0.048 + 0.043 = 0.048 / 0.091 = 0.53
P(No/ Given Rainy and Cool) = 0.043 / 0.048 + 0.043 = 0.043 / 0.091 = 0.47
So now you can see the posibility of Yes is > than 0.5 which is the Answer.
If the weather is Rainy and Cool what will the person do -> He can play Golf假设您获得了新的测试数据,并且获得了阴天和温和的数据,那么输出是什么?我们将使用贝叶斯定理尝试找到它。
P(是/鉴于阴天和温和)?
P(Yes/ Overcast and Mild) = P(Yes) * P(Overcast / Yes) * P(Mild / Yes)
---------------------------------------
P(Overcast) * P(Mild)
Now you know that P(Overcast) * P(Mild) is a constant (For no also you will get the same value)
P(Yes/ Overcast and Mild) = P(Yes) * P(Overcast / Yes) * P(Mild / Yes)
P(Yes/ Overcast and Mild) = 9/14 * 4/9 * 4/9
= 8/63 = 0.127
P(No/ Given Overcast and Mild) = P(No) * P(Overcast/ No) * P(Mild / No)
= 5 /14 * 0/5 * 2/5 = 0
P(Yes/ Given Overcast and Mild) = 0.127
P(No/ Given Overcast and Mild) = 0
Nomalize the values
---------------------
P(Yes/ Given Overcast and Mild) = 0.127 / 0.127 + 0 = 0.127 / 0.127 = 1
P(No/ Given Overcast and Mild) = 0 / 0.127 = 0
So now you can see the posibility of Yes is > than 0.5 which is the Answer.
If the weather is Overcast and Mild what will the person do -> He can play Golf2.4 贝叶斯定理实时应用
贝叶斯定理的众多应用之一是贝叶斯推理,这是一种特殊的统计推理方法。贝叶斯推理已应用于各种活动,包括医学、科学、哲学、工程、体育、法律等。例如,我们可以使用贝叶斯定理通过考虑任何给定的人有多大可能来定义医学测试结果的准确性。有疾病和测试的总体准确性。贝叶斯定理依赖于合并先验概率分布来生成后验概率。在贝叶斯统计推断中,先验概率是收集新数据之前事件的概率。
尝试使用贝叶斯定理找到这些问题的答案。使用评论部分给出答案或提出问题。
- A、B、C 三人应聘一家私营公司的工作。他们选择的机会比例为1:2:4。A、B、C 能够引入变革以提高公司利润的概率分别为0.8、0.5 和0.3。如果没有发生变化,求由于 C 的任命而导致变化的概率。
- 一袋包含 4 个球。随机抽取两个球,不放回,发现是蓝色的。袋子里所有球都是蓝色的概率是多少?
- 在一个社区,90% 的儿童因流感而生病,10% 则因麻疹而没有其他疾病。麻疹出现皮疹的概率为 0.95,流感出现皮疹的概率为 0.08。如果孩子出现皮疹,请计算孩子患流感的可能性。
- A店里有30罐纯酥油和40罐掺假酥油在售,B店里有50罐纯酥油和60罐掺假酥油。随机从其中一家商店购买一罐酥油,发现掺假。求从商店 B 购买的概率。
- 一包 52 张卡片中丢失了一张卡片。从剩下的牌中,随机抽出两张,发现都是梅花。求丢失的卡片也是梅花的概率。
- 一个袋子里有 4 个球。随机抽取两个球(不放回),发现它们是红色的。袋子里所有球都是红色的概率是多少?
三、K-最近邻算法(KNN)
KNN 算法是分类和回归问题的简单而有效的解决方案。我们首先讨论第一个分类问题。假设我们有一个包含两组数据点的二元分类问题。现在,假设我们引入一个新的数据点。如何判断它是否属于这两个类别之一?如果我们使用逻辑回归,我们可以将这些数据点按一条线划分,但这种情况需要不同的方法。这就是K 最近邻发挥作用的地方。
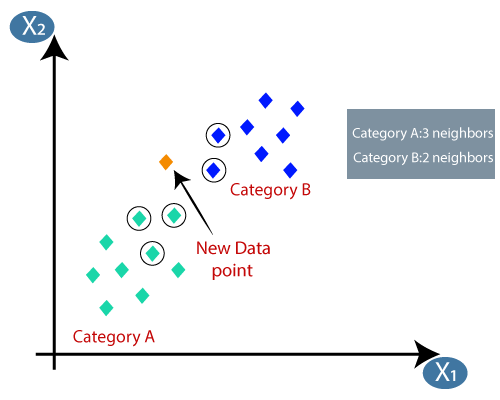
K-近邻是一种简单的算法,它的工作原理是取离我们最近的五个点(这里K 值为 5。K 是一个次要参数),它代表我们最近的点。在这种情况下,我们可以看到最大数量的点来自绿色类别(A 类),只有 3 个点。我们将新数据点分类为属于 K 值的最大点数。为了实现这一点,我们使用两个特定距离,
- 欧氏距离
- 曼哈顿距离
计算两点之间的欧氏距离,表示为
d = √[ (x2– x1)^2 + (y2– y1)^2].另一方面,对于曼哈顿距离,我们计算两点之间的距离。
d = |x1 - x2| + |y1 - y2|这两个距离的区别在于我们没有计算假设距离。

这些方法用于分类问题。对于回归,我们使用不同的方法。
对于回归,我们将K 值设为 3。我们取最近的 3 个点来计算一个新的数据点。K是一个超参数,表示最近点的数量。如果我们需要计算一个新数据点的输出,我们找到最近的K个点,然后计算它们的平均值以获得输出值。
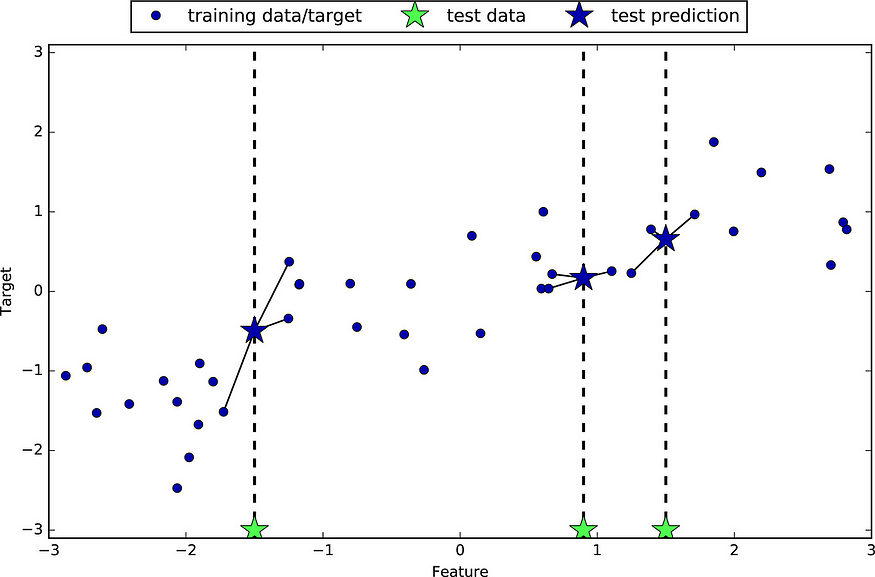
我们计算的 K 值等于 1 到 50,然后我们可能尝试检查错误率,如果错误率小于 only,我们选择该模型。
关于 K 最近邻的另外两件事效果非常糟糕
- 异常值
- 数据集不平衡
因此,KNN 的局限性在于,由于不平衡或离群数据集的存在,它可能会对点进行错误分类。
异常值
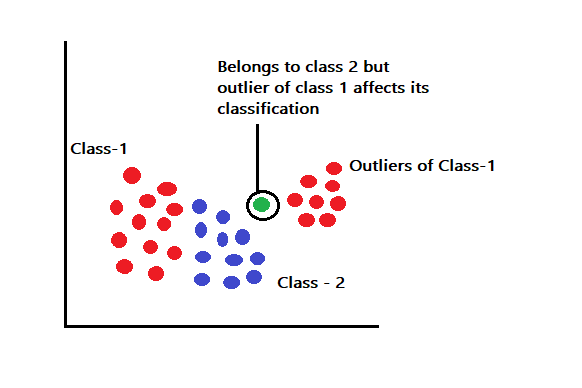
考虑上面的图像具有属于 -1 类的异常值。假设我们想要预测 1 类标记的异常值和 2 类标记的训练点之间的点。测试点可能属于 2 类标签,但由于存在 1 类异常值,这些点可能会被错误地分类为 1 类。
不平衡

考虑样本空间中大约有 1000 个点被分类为A 类或 B 类的情况。假设在 1000 个点中,有 800 个点属于 A 类,这表明数据集高度不平衡。这会影响新测试样本的分类吗?是的,考虑一下我们想要在样本空间中找到点 X 的类标签。如果我们认为 k 值非常大,比如 150 左右,那么不平衡的数据集将迫使 X 点落入A 类,这可能会导致错误分类。
如何选择最佳的K值?
k 的最佳值是提供最小误差和最大精度的值。我们重点关注随机取一组 k 值,并验证在训练和测试模型时我们获得最小错误率的 k 值。这就是朴素贝叶斯算法和 K 最近邻算法。我希望你能很好地理解这两种理论。
KNN中如何找到K的最优值?