各种滤波算法的比较（GF、KF、EKF、UKF、PF），内附简单实现代码

news2024/11/24 8:25:49

一、前言

二、滤波算法介绍

1、GF（高斯滤波）

2、KF（卡尔曼滤波）

3、EKF（可扩展卡尔曼滤波）

4、UKF（无迹卡尔曼滤波）

5、PF（粒子滤波）

三、不同滤波算法对比

四、不同滤波算法的表现

五、简单实现

一、前言

为了使基于RSSI/CSI等室内定位的结果更加地稳定，让滤波后的RSSI/CSI值更接近真实值，针对不同场景引入合适的滤波算法是很有必要的。当然文章并非只针对室内定位这个领域，其它领域，特别是信号或者通信领域，了解各种滤波算法也是非常重要的！

二、滤波算法介绍

1、GF（高斯滤波）

高斯滤波是一种根据高斯函数的形状来选择权值的线性平滑滤波器，它对抑制服从正态分布的噪声非常有效，从而达到平滑数据的目的。

2、KF（卡尔曼滤波）

卡尔曼滤波算法是一种抑制高斯噪声有效的最优化自回归数据处理算法，对于系统过程的滤波比较好，能够有效滤除信号发生的突变。并且对于变化快速、实时更新的线性系统有着非常好的寻优及滤波效果。

卡尔曼滤波原理的详细解释可参考下面文章：

CSI数据预处理之卡尔曼滤波、高斯滤波、简单平均-CSDN博客

3、EKF（可扩展卡尔曼滤波）

扩展卡尔曼滤波器是对KF的改进衍生，它将非线性函数进行泰勒展开，然后省略高阶项，保留展开项的一阶项，以此来实现非线性函数线性化，最后通过卡尔曼滤波算法近似计算系统的状态估计值和方差估计值。

4、UKF（无迹卡尔曼滤波）

无迹卡尔曼滤波算法也是对KF的改进衍生，它舍弃了EKF算法的线性化过程，采用无迹变换（Unscented Transform，UT）巧妙地避免了线性化所带来的误差，同时减少了算法的复杂度（UKF不需要在每个实例中计算雅可比矩阵），克服了EKF算法的估计精度低、稳定性差的缺陷。

5、PF（粒子滤波）

粒子滤波法是指通过寻找一组在状态空间传播的随机样本对概率密度函数进行近似，以样本均值代替积分运算，从而获得状态最小方差分布的过程。和其它非线性滤波方法相同，它也是一种次优的滤波方法

三、不同滤波算法对比

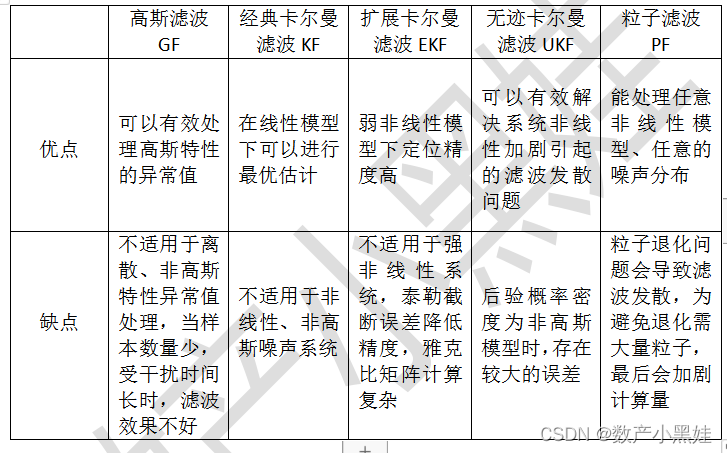
四、不同滤波算法的表现

五、简单实现

本文就是做一个简单实现，其中高斯滤波和卡尔曼滤波比较基础，就不再展示。首先，定义一个简单的非线性状态空间模型，例如一个带有噪声的一维运动模型：

% 非线性状态空间模型
A = 1;  % 状态转移矩阵
B = 0;  % 控制输入矩阵
H = 1;  % 观测矩阵
% 状态转移方程
f = @(x) A*x + B*randn;
% 观测方程
h = @(x) H*x + randn;

可扩展卡尔曼滤波：

% 初始状态和协方差
x0 = 0;
P0 = 1;
% EKF算法
x_EKF = zeros(1, 100);  % 存储估计状态
P_EKF = zeros(1, 100);  % 存储估计协方差
x_pred = x0;
P_pred = P0;
for k = 1:100
    % 预测步骤
    x_pred = f(x_pred);
    P_pred = A*P_pred*A';
    % 更新步骤
    K = P_pred*H'/(H*P_pred*H' + 1);
    z = h(x_pred);
    x_pred = x_pred + K*(z - H*x_pred);
    P_pred = (1 - K*H)*P_pred;
    x_EKF(k) = x_pred;
    P_EKF(k) = P_pred;
end

无迹卡尔曼滤波：

% UKF算法
x_UKF = zeros(1, 100);  % 存储估计状态
P_UKF = zeros(1, 100);  % 存储估计协方差
% 参数设置
alpha = 1e-3;
beta = 2;
kappa = 0;
% 初始化Sigma点
n = numel(x0);
lambda = alpha^2 * (n + kappa) - n;
weights = 1 / (2 * (n + lambda)) * ones(1, 2*n+1);
weights(1) = lambda / (n + lambda);
X = zeros(n, 2*n+1);
X(:,1) = x0;
P_sqrt = chol(P0, 'lower');
for i = 1:n
    X(:,i+1) = x0 + sqrt(n + lambda) * P_sqrt(:,i);
    X(:,n+i+1) = x0 - sqrt(n + lambda) * P_sqrt(:,i);
end
for k = 1:100
    % 预测步骤
    X_pred = zeros(size(X));
    for i = 1:2*n+1
        X_pred(:,i) = f(X(:,i));
    end
    x_pred = X_pred * weights';
    P_pred = zeros(size(P0));
    for i = 1:2*n+1
        P_pred = P_pred + weights(i) * (X_pred(:,i) - x_pred) * (X_pred(:,i) - x_pred)';
    end
    % 更新步骤
    Z = zeros(1, 2*n+1);
    for i = 1:2*n+1
        Z(i) = h(X_pred(:,i));
    end
    z_pred = Z * weights';
    Pzz = zeros(size(H*P_pred*H'));
    Pxz = zeros(size(P_pred));
    for i = 1:2*n+1
        Pzz = Pzz + weights(i) * (Z(i) - z_pred) * (Z(i) - z_pred)';
        Pxz = Pxz + weights(i) * (X_pred(:,i) - x_pred) * (Z(i) - z_pred)';
    end
    K = Pxz / Pzz;
    x_pred = x_pred + K * (h(x_pred) - z_pred);
    P_pred = P_pred - K * Pzz * K';
    
    x_UKF(k) = x_pred;
    P_UKF(k) = P_pred;
end

粒子滤波：

% PF算法
x_PF = zeros(1, 100);  % 存储估计状态
P_PF = zeros(1, 100);  % 存储估计协方差
% 参数设置
num_particles = 1000;
% 初始化粒子
particles = randn(1, num_particles);
for k = 1:100
    % 预测步骤
    particles = f(particles);
    % 更新步骤
    weights_PF = exp(-(h(particles) - 1).^2 / (2 * 1^2));  % 高斯权重函数
    % 归一化权重
    weights_PF = weights_PF / sum(weights_PF);
    % 重采样
    indices = randsample(1:num_particles, num_particles, 'true', weights_PF);
    particles = particles(indices);
    % 估计状态和协方差
    x_PF(k) = mean(particles);
    P_PF(k) = var(particles);
end

生成符合高斯分布的状态和观测值：

% 生成符合高斯分布的状态和观测值
true_states = zeros(1, 100);
observations = zeros(1, 100);
true_states(1) = randn();  % 初始状态符合高斯分布
observations(1) = true_states(1) + 0.5*randn();  % 初始观测值加入噪声
for k = 2:100
    % 状态转移模型
    true_states(k) = 0.9 * true_states(k-1) + 0.1 * randn();
    % 观测模型
    observations(k) = true_states(k) + 0.5*randn(); % 添加观测噪声
end

三种滤波算法可视化：

% 画图
figure;
subplot(3,1,1);
plot(1:100, true_states, 'LineWidth', 1.2, 'DisplayName', 'True State');
hold on;
plot(1:100, x_EKF, 'LineWidth', 1.2, 'DisplayName', 'EKF');
title('Extended Kalman Filter (EKF)');
xlabel('Time step');
ylabel('State');
legend;
subplot(3,1,2);
plot(1:100, true_states, 'LineWidth', 1.2, 'DisplayName', 'True State');
hold on;
plot(1:100, x_UKF,  'LineWidth', 2, 'DisplayName', 'UKF');
title('Unscented Kalman Filter (UKF)');
xlabel('Time step');
ylabel('State');
legend;
subplot(3,1,3);
plot(1:100, true_states, 'LineWidth', 1.2, 'DisplayName', 'True State');
hold on;
plot(1:100, x_PF, 'LineWidth', 2, 'DisplayName', 'PF');
title('Particle Filter (PF)');
xlabel('Time step');
ylabel('State');
legend;

效果：