论文地址:https://arxiv.org/pdf/1911.09016v1.pdf(下文中提及的引用信息如未解释,请索引原论文末的参考文献)
论文中提到的SSTD2019@Multi-Source Spatial Entity Linkage (提取码:i3xt)
论文重要部分翻译
Abstract
除了传统的制图数据源,空间信息也可以从基于位置的数据源中获取。
然而,即使不同的基于位置的数据源指代的是同一个物理世界,但每个数据源都只覆盖了空间实体的一部分,且用不同的属性描述它们,有时会提供相互矛盾的信息。
因此,我们引入空间实体链接问题——找出哪些空间实体对属于同一个物理空间实体。
我们提出的解决方案 (QuadSky)
- 从时间效率高的空间分块技术 (QuadFlex) 开始
- 对同一块中的空间实体进行成对比较
- 使用帕累托最优性(Pareto optimality)和 SkyRank 算法对pairs进行排序
- 最后,使用我们新颖的 SkyEx-* 系列算法对pairs进行分类
对 1,500 对手动标记的数据集产生 0.85 的精度和 0.85 的召回率,对 777,452 对半手动标记数据集产生 0.87 的精度和 0.6 的召回率。
INTRODUCTION
网络数据和社交网络在信息量和异质性方面都在增长。 几乎所有在线资源都提供了引入位置的可能性(带有语义细节的地理标记实体)。 主要关注位置的特定类型的数据源是基于位置的数据源,例如 Google Places、Yelp、Foursquare 等。
与制图数据源相比,基于位置的数据源中的位置具有介于空间对象和实体之间的混合形式。 我们将它们称为空间实体,因为
- 它们位于空间位置
- 但也由其他属性(例如位置名称、地址、关键字等)标识。
空间实体在依赖地理信息,比如选择有影响力地点的地理推荐、使用地理偏好的搜索引擎的等等多个系统中发挥关键作用。
然而,虽然空间对象仅由坐标标识,但空间实体并非如此。
- 不同的空间实体可能在相同的坐标中共存(购物中心中的商店)
- 或者相同的实体可能位于不同但处于附近的坐标(因为来自不同数据源的缘故,每个数据源里可能标注的坐标信息有出入,但是指的是一个空间实体,结合后面例子理解)(例如,“Chicago Roasthouse”出现在 Yelp 和 Google Places 中,坐标相距 82 米)
空间实体的身份是几个属性的组合。
不幸的是,由于数据源内部和数据源之间的不一致,有时难以推断空间实体的身份。
每个基于位置的数据源都包含不同的属性;某些属性可能会丢失,甚至相互矛盾。例如:
- 源 A 在 (57.436 10.534) 中包含空间实体“Lygten”,其关键字为“咖啡”、“茶”和“可可和香料”
- 而源 B 在 (57.435 10.533) 中包含“Restaurant Lygten”,其关键字为关键词“餐厅”
We need a technique that can automatically decide whether these two spatial entities are the same realworld entity.我们需要一种能够自动确定这两个空间实体是否是同一个现实世界实体的技术。
The problem of finding which spatial entities belong to the same physical entity is referred to as spatial entity linkage or spatial entity resolution. 找出哪些空间实体属于同一个物理实体的问题称为空间实体链接或空间实体解析。
(We use the term entity linkage since we do not merge the entities.
我们使用术语实体链接,因为我们不合并实体。)
(有几项工作将实体链接应用于各个领域,但在空间实体方面的工作很少,尽管它们是地理相关研究的核心。实体联动研究中的实体大多是指人;因此,方法和模型是基于同一个人的两份记录所揭示的相似性。此外,这些作品没有解决空间实体的空间特征。至于空间实体集成方面的工作,它们的主要贡献是工具而不是算法。更重要的是,这些方法提出了任意属性权重和评分函数,无需实验或评估。与[11-13]相比,[10]中提出的基于天际线的算法(SkyEx)没有评分函数和半任意权重,并且取得了很好的效果。然而,SkyEx 取决于天际线 k 的阈值数量,这只能通过实验发现,因为作者没有提供估计 k 的方法。综上所述,一方面,空间实体的信息量越来越多,无论是单一来源还是跨来源,都可以提高地理信息的质量;另一方面,空间实体联动问题难以解决,不仅是因为数据的异质性,还因为缺乏合适有效的方法。)
在本文中,我们解决了跨不同基于位置的数据源的空间实体链接问题。我们显著扩展了之前的会议论文[SSTD2019@Multi-Source Spatial Entity Linkage]。
作为基于[SSTD2019@Multi-Source Spatial Entity Linkage]的整体解决方案
- 首先,我们提出了一种使用地理坐标将空间实体组织成块的方法
- 然后,我们成对比较空间实体的属性
- 之后,我们使用我们的新技术 SkyRank 根据pairs的相似性对pairs进行排名
- 最后,我们介绍了三种方法(SkyEx-F、SkyEx-FES、SkyEx-D)来确定比较实体对(pairs)是否属于同一个物理实体。
我们的贡献是:
- 我们引入了 QuadSky,一种连接空间实体的技术,我们根据来自四个基于位置的数据源的真实数据对其进行评估
- 我们提出了一种称为 QuadFlex 的算法,它根据空间实体的空间接近度将空间实体组织成块,保持四叉树的复杂性并避免将附近的点分配到不同的块中
- 根据相似度对pairs进行排序,我们提出了一种基于帕累托最优(Pareto optimality)概念的灵活技术(SkyRank)
- 为了标记pairs,我们提出了 SkyEx-* 系列算法,该算法考虑了pairs的排序顺序并固定了一个截止水平来分离类别
- 我们介绍了两种基于阈值的算法:SkyEx-F,它使用 F-measure 来分离类;以及 SkyEx-FES(SkyEx-F 的优化版本),为剪除 SkyEx-F 73% 的天际线探索提供了理论保证
- 我们提出了 SkyEx-D,这是一种完全无监督且无参数的新算法,用于分离类别。
贡献 1 和 2 来自 [SSTD2019@Multi-Source Spatial Entity Linkage],贡献 5 和 6 是新的,与 [SSTD2019@Multi-Source Spatial Entity Linkage] 相比,贡献 3 和 4 有显着改进。与baselines相比,[SSTD2019@Multi-Source Spatial Entity Linkage] 中的工作报告了非常好的结果,但有以下限制:提出的基于阈值的标记算法 SkyEx 需要天际线的阈值数量 k 作为输入,并且没有关于如何修复 k 的建议解决方案,除了尝试不同的值。我们通过首先修改 [SSTD2019@Multi-Source Spatial Entity Linkage] 中的原始 SkyEx 来解决此限制,使其仅对pairs进行排名而不标记,我们将其称为 SkyRank。然后,我们将分类问题委托给三种新算法,即 SkyEx-F、SkyEx-FES 和 SkyEx-D。 [SSTD2019@Multi-Source Spatial Entity Linkage] 中的实验尝试使用精度、召回率和 F-measure 来修复 k。我们现在在我们新颖的 SkyEx-F 算法中形式化了这个基本原理。我们通过提供在探索整个数据集之前可以停止 SkyEx-F 的理论保证来进一步改进,并提出优化的 SkyEx-FES,它可以修剪 80% 的 SkyEx-F 天际线探索。此外,我们引入了一种估计天际线数量的新方法(SkyEx-D),它是完全无监督和无参数的,并且非常接近基于阈值的版本(SkyEx-F 和 SkyEx-FES)。在本文中,我们为 SkyEx-FES 和 SkyEx-D 提供了一组新的实验,并与 SkyEx-F、监督学习和聚类技术进行了比较。
RELATED WORK
在本节中,我们描述了一些关于实体解析、空间数据集成和空间实体链接的工作。
实体解析“Entity resolution”:实体解析问题在文献中被提及,包括重复数据删除、实体链接和实体匹配 [4, 15]。实体解析已用于各个领域,例如社交网络中的匹配配置文件 [2]、生物信息学数据 [3]、生物医学数据 [16]、出版物数据 [4、5]、家谱数据 [6]、产品数据 [4、 5]等。比较实体的属性,并分配相似度值。是否链接两个实体的决定通常基于评分函数。然而,找到一个合适的相似性函数来结合属性的相似性并决定是否链接实体通常是困难的。一些工作使用训练集来学习classifier(分类器) [7, 8, 17],其他工作基于通过实验得出的阈值做出决定 [9, 18]。其他方法决定将匹配的不确定性纳入决策[19]。最后,匹配实体也可以基于oracle(预言机) [4, 5] 或用户 [5] 的反馈。
空间数据集成“Spatial data integration” : 有几项关于整合纯空间对象的工作。 空间对象与空间实体的不同主要是因为空间对象完全由其坐标或其空间形状决定,而空间实体除了位于地理位置之外,还具有明确定义的identity(姓名、电话、类别)。 空间对象集成的工作旨在从单个/多个数据源创建空间对象的统一空间表示。 al [20] 的 Schafers 使用规则集成道路网络,以根据长度、角度、形状以及街道名称(如果可用)的相似性来检测匹配和不匹配的道路。 [21-24] 中的解决方案是纯空间的,并讨论了源自传感器和雷达的空间对象的集成,以便在 2D 甚至 3D 中更好地表示表面。 这些方法不适用于空间实体。
空间实体链接“Spatial entity linkage”:在 [11-14, 25, 26] 中专门解决了空间实体对实体解析问题的挑战。 [25]中的工作是空间数据集成和空间实体链接工作之间的桥梁,因为实体具有名称、坐标和类型,但与空间对象类似,它们指的是景观(河流、沙漠、山脉等)。 . [25] 中使用的方法是有监督的,需要标记数据。此外,甚至属性“类型”的相似性也是通过训练集来学习的。关于[11-13],这些工作的主要贡献在于设计空间实体匹配工具而不是集成算法。在[13]中,半径内的空间实体相互比较,半径的值根据空间实体的类型是固定的。例如,餐厅和酒店的半径为 50 m,而公园的半径为 500 m。所有属性(坐标除外)都使用 Levenshtein 相似度进行比较。由于实体的名称、地理数据和类型始终存在,因此它们在评分函数中占据了三分之二的权重,而网站、地址和电话号码的权重则调整为三分之一。 [12] 中的空间实体匹配原型依赖于一种技术,该技术任意使用所有文本属性的相似度得分的平均值,而不提供对该选择的讨论。与 [11, 12] 类似,[13] 中工作的主要贡献是设计用于空间实体集成的工具。底层算法考虑彼此相距 5 m 的空间实体,并在语法上比较实体的名称和在语义上与实体相关的元数据。最后,使用信念理论[26]做出决定。 [11-13] 中的工作缺乏对算法的评估。 [SSTD2019@Multi-Source Spatial Entity Linkage] 中的工作提出了一种可扩展的基于空间四叉树的分块技术,该技术不仅可以固定空间实体之间的距离,还可以控制块的密度。然后,对同一块的空间实体的名称(Levenshtein)、地址(自定义)和类别(Wu&Palmer 使用 Wordnet)进行比较。最后,使用基于阈值的算法 (SkyEx) 来分离类别。然而,SkyEx 并没有为每个属性相似性使用固定阈值,而是将相似性抽象为天际线,并且只需要一个阈值数量的天际线 k 来分离类。作者提供了实验和评估,然而,他们缺乏固定 k 的估计技术。本论文使用[SSTD2019@Multi-Source Spatial Entity Linkage]中的解决方案进行空间分块和成对比较。我们在 SkyEx 中使用天际线进行标记过程,但我们提出了三种新算法(SkyEx-F、SkyEx-FES 和 SkyEx-D)来分离类,并在内部固定 k。
总结“Summary”。一般实体解析方法提出了有意义的解决方案,但它们没有考虑空间实体的空间特征。 大多数旨在匹配代表个人的实体(社交网络中的个人资料、作者和出版物、医疗记录、家谱联系等),甚至连接自然界中的物种。 个人实体解析的建议解决方案,无论是监督还是基于实验阈值,都是在人类实体数据集上学习的。 不能仅仅假设人类实体数据集中的行为与空间实体的行为相似。 自然界中物种的解决方案基于特定领域的算法,在其他领域几乎没有适用性。 空间实体方面的具体工作很少[11-13],主要集中在空间数据集成的工具上,而不是算法上。 在所有这些工作中,评分函数都是任意选择的,没有提供评价。
SPATIAL ENTITY LINKAGE 空间实体链接
在本节中,我们将介绍问题定义和我们的整体解决方案。 这项工作中使用的基本概念:
- spatial entity空间实体:such as places, businesses, etc. Spatial entities originate from location-based sources, e.g., directories with location information (yellow pages, Google Places, etc.) and location-based social networks (Foursquare, Gowalla, etc.).
例如地点、企业等。空间实体源自基于位置的数据源,例如具有位置信息的目录(黄页、Google Places 等)和基于位置的社交网络 (Foursquare、Gowalla 等)。
“Definition 1.” 空间实体 s s s 是在源 I I I 内唯一标识的实体,位于地理点 p p p 中,并伴有一组属性 A = a i A = {a_{i}} A=ai
与
s
s
s相关的属性可以分类为:
空间的:实体所在的点,以经纬度表示;
文本的:名称、地址、网站、描述等文本形式的属性;
语义的:文本形式的属性,丰富空间实体背后的语义,例如类别、关键字、元数据等;
日期、时间或数字:有关空间实体的其他详细信息,例如电话、营业时间、成立日期等。
源自 Yelp 的空间实体的示例可以是点 (56.716 10.114) 中名为“Star Pizza”的地方,关键字为“pizza, fast food”,地址为“Storegade 31”。 在 Yelp 或其他来源中可以再次找到相同的空间实体,有时具有相同的属性、更多、更少,甚至具有矛盾值的属性。 因此,需要一种能够以智能方式统一不同来源内和跨不同来源的信息的方法。
“Problem definition” :给定一组来自多个数据源的空间实体 S S S,空间实体链接问题旨在找到那些引用相同物理空间实体的空间实体对 < s i s_{i} si, s j s_{j} sj>。
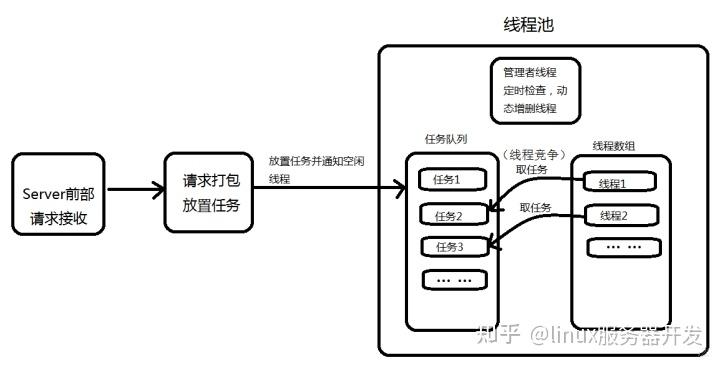
我们提出了 QuadSky,这是一种基于四叉树数据分区和天际线探索的解决方案。总体方法如图 1 所示:

QuadSky 由四个主要部分组成:
- 空间分块 (QuadFlex)
- 成对比较
- 对pairs进行排序 (SkyRank)
- 对pairs进行标记(SkyEx-* 系列算法)
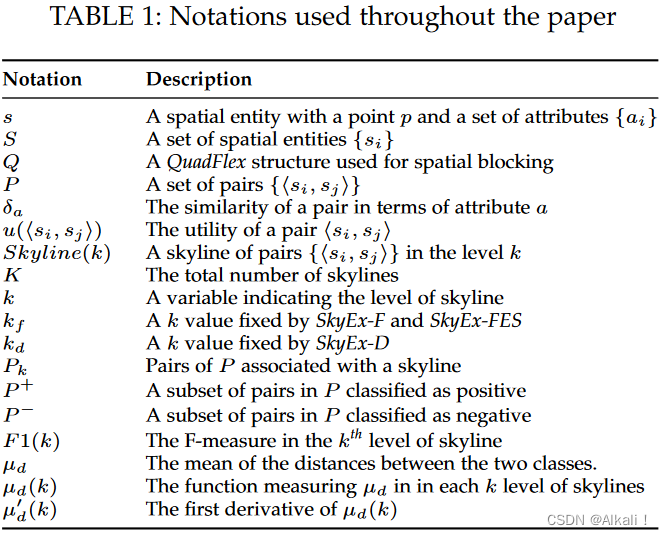
S S S 包含所有空间实体。我们提出了 QuadFlex,这是一种基于四叉树的解决方案,可以通过考虑/衡量/评估空间实体之间的距离和区域的密度来执行空间分块。 QuadFlex 的输出是含有 位于附近的空间实体 的叶子列表。在叶子中,我们执行属性的成对比较。然后,我们使用 SkyRank 算法根据天际线(第 6 节中详述的概念)对比较的pairs进行排名。为了决定哪些对决定匹配,哪些不决定匹配,我们提出了 SkyEx-* 系列算法(SkyEx-F、SkyEx-FES 和 SkyEx-D),该算法可以找到哪个天际线标准最好地将引用自相同物理空间实体的pairs与其余部分分开。在以下部分中,我们将详细介绍 QuadSky 的每个阶段。我们使用表 1 中的符号(我们将在本文中逐步解释它们)。
SPATIAL BLOCKING 空间分块
由于空间接近度是找到匹配项的重要指标,因此第一步是将附近的空间实体分组为块。 [27, 28] 中讨论了几种通用的分块技术,但主要基于文本属性,不适用于空间分块。我们提出了一种基于四叉树的解决方案(QuadFlex),它使用树数据结构,但也保留了空间实体的空间邻近性。
四叉树是一棵树,当容量被填满时,它的节点总是递归地分成四个孩子[29]。四叉树构建完成后,落入同一片叶子的点在空间上就在附近。因此,这些叶子是空间块的良好候选者。然而,现有的四叉树算法需要适应空间分块。
- 首先,四叉树需要容量(点数)作为参数。容量对于空间分块来说不是一个有意义的参数,而区域的密度是一个更好的候选者。例如,如果该区域过于密集(例如,市中心),即使容量未达到,进一步拆分也会更有利。相反,乡村中的两个点(例如农场)可能相距较远,但它们仍然可能是同一个实体。
- 其次,四叉树不限制点之间的距离。即使两点可能在一个考虑密度的区域中,如果它们彼此相距很远,则没有必要比较它们。子节点中两点之间的最大距离是该区域的对角线(所有四叉树子节点都是矩形)。我们使用区域的对角线 m 作为控制点距离的参数,而不是比较所有空间实体之间的所有距离。
- 最后,四叉树分裂成四个孩子,有时附近的点可能会落入不同的叶子。我们通过允许多个分配来修改将点分配给孩子的过程。
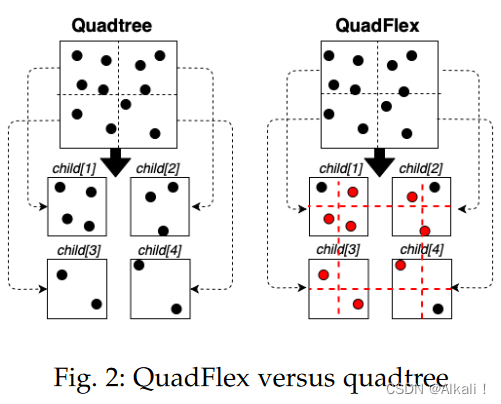
图 2 显示了我们为我们的版本 QuadFlex 构建传统四叉树所做的修改。 传统的四叉树将每个父级的区域划分为四个较小的区域,即子级。 一个点只属于一个孩子。 在我们的修改中,该区域将以与四叉树相同的方式拆分为 4 个子节点(高度为父节点的 0.5,宽度为父节点的 0.5),但是当我们将一个点分配给一个孩子时,我们会考虑在当前孩子中也包括那些在边界附近的点。 例如,在图 2中,QuadFlex 以与四叉树相同的方式进行物理拆分,但红色虚线表示将考虑包含相邻点的区域。

红点位于重叠区域,将包含在多个子项中。算法 1 详细介绍了使用 QuadFlex 检索空间块的过程。该算法使用数据和参数
m
m
m 和
d
d
d 的边界框(第 1 行)创建 QuadFlex 树的根。然后,它将每个空间实体插入到 QuadFlex(第 3 行)中,最后返回其叶子。方法 insert(s) 和 getIndex(s) 是对 QuadFlex 对象 (this) 的自调用。插入过程类似于传统的四叉树,只是约束不是容量,而是区域的对角线
m
m
m(点之间的最大距离)和区域的密度
d
d
d。因此,如果 QuadFlex 的对角线大于距离
m
m
m 或密度大于我们定义的值
d
d
d(第 12 行),则 QuadFlex 类似于四叉树,将分裂为四个孩子。然而,与传统的四叉树相比,一个空间实体可能属于多个孩子。 getIndex(s) 方法获取将分配新点的子项的索引列表。尽管 Q 以与四叉树相同的方式拆分为 4 个孩子,但垂直左、垂直右、水平向上和水平向下的线允许区域的逻辑重叠,因此相邻空间实体不会被分离。
PAIRWISE COMPARISONS 成对比较
在空间分块之后,我们对落入同一片叶子的空间实体进行成对比较。 接下来,我们描述不同类型属性的度量。
文本相似性 “Textual Similarity”
我们使用单词之间的编辑距离来测量空间实体的文本相似性。
字符串
s
1
s1
s1 和字符串
s
2
s2
s2 之间的
L
e
v
e
n
s
h
t
e
i
n
Levenshtein
Levenshtein 距离
d
(
s
1
,
s
2
)
d(s1, s2)
d(s1,s2) 是将字符串
s
1
s1
s1 转换为字符串
s
2
s2
s2 所需的编辑次数(插入、删除、更改字符)。 我们将相似度定义为:
T e x t S i m ( s 1 , s 2 ) = ( 1 − d ( s 1 , s 2 ) m a x ( ∣ s 1 ∣ , ∣ s 2 ∣ ) ) TextSim(s_{1},s_{2})=(1-\frac{d(s_{1},s_{2})}{max(|s_{1}|,|s_{2}|)}) TextSim(s1,s2)=(1−max(∣s1∣,∣s2∣)d(s1,s2))
示例 1. 让我们考虑“Skippers Grill”和“Skippers Grillbar”。
将“Skippers Grill”转换为“Skippers Grillbar”的 Levenshtein 距离为 3(3 次插入)。
第一个和第二个字符串的长度分别是 14 和 17。
所以,TextSim(”Skippers Grill”, “Skippers Grillbar”) = 1 - (3/max(14, 17) = 0.8235。
请注意,并非所有文本属性都可以类似地处理。字符串相似度指标通常适用于名称、用户名等属性。其他一些文本属性需要其他需要定制的指标。在本文中,我们将地址视为特定的文本属性。两个地址之间的相似性不能用 Levenshtein、Jaccard、Cosine 等来衡量,因为地址的微小变化可能是实体之间空间距离的巨大差距。例如,“Jyllandsgade 15 9480 Løkken”和“Jyllandsgade 75 9480 Løkken”的距离为 1,Levenshtein 相似度为 0.963,但相距 650 米。然而,“Jyllandsgade 15 9480 Løkken”和“Jyllandsgade 15 9480 Løkken Denmark”的距离为 8,Levenshtein 相似度为 0.772,但它们是同一栋建筑。在 [11, 12] 中,地址被认为是另当别论的文本属性。在我们的例子中,我们执行了一些数据清理(删除逗号、标点符号、小写字母等),然后我们搜索字符串的相等性或包含性。在相等的情况下,我们指定相似度为 1.0,在包含的情况下为 0.9,否则为 0.0。
语义相似度 “Semantic Similarity”
类别、关键字或元数据等字段的相似性不能仅在语法上进行比较。 有时,使用几个同义词来表达相同的想法。 因此,我们需要找到一个相似性而不是考虑同义词。 我们使用 Wordnet [31] 来检测两个单词之间的关系类型和 Wu & Palmer 相似性度量 (wup) [32]。 两个空间实体之间的语义相似度是它们的类别、关键字或元数据列表之间的最大相似度。 空间实体 s1 和 s2 的语义相似度为:
S
e
m
S
i
m
(
s
1
,
s
2
)
=
m
a
x
{
w
u
p
(
c
i
,
c
j
)
}
SemSim(s_{1},s_{2})=max\{wup(c_{i},c_{j})\}
SemSim(s1,s2)=max{wup(ci,cj)}
where
c
i
∈
C
1
c_{i}∈C_{1}
ci∈C1 and
c
j
∈
C
2
c_{j}∈C_{2}
cj∈C2 and
C
1
C_{1}
C1 is the set of keywords of
s
1
s_{1}
s1
and
C
2
C_{2}
C2 is the set of keywords of
s
2
s_{2}
s2.
示例 2. 让我们以两个空间实体 s1 和 s2 及其对应的语义信息表示为关键字 C1 = {”restaurant”,
“italian”} 和 C1 = {”food”, “pizza”} 的示例。 每对之间的相似度为 wup(”restaurant”,
”food”) = 0.4, wup(”italian”, ”food”) = 0.4286, wup(”restaurant”,
”pizza”) = 0.3333 和 wup(”italian” , “pizza”) = 0.3529。
最后,s1和s2的语义相似度为SemSim(s1, s2) = max{0.4, 0.4286, 0.3333, 0.3529} =
0.4286。
日期、时间或数字相似度 “Date, Time, or Numeric Similarity” (本文的算法中不用计算)
表示为数字、日期、时间或间隔的两个字段之间的相似性是一个布尔决策(真或假)。 尽管这些字段的相似性仅依赖于相等性检查,但大部分精力都放在了数据准备上。 例如,应该从前缀中识别和清除不同的电话格式。 间隔(营业时间)等其他数据格式可能需要对间隔的相似性、包含和交集进行时间查询。 在本文中,我们不计算这些属性之间的相似性,因为我们使用它们来构建基本事实(ground truth)。
RANKING THE PAIRS 对pairs进行排名
在成对比较之后,这些pairs有 n n n 个相似度值,每个被考虑其相似性的属性有一个相似度值。我们将属性 a a a 的两个空间实体的相似性表示为 δ a δ_{a} δa。例如,一对 < s 1 , s 2 > <s_{1}, s_{2}> <s1,s2> 表示为 δ a 1 , . . . , δ a n {δ_{a_{1}} , ..., δ_{a_{n}} } δa1,...,δan。我们需要解决的问题是,哪些 < s i , s j > <s_{i}, s_{j}> <si,sj> 对表示要考虑匹配的强相似性。相关的工作解决方案建议使用分类器 [7, 8, 33] 或尝试不同的阈值 [9, 18, 33]。我们提出了一种更轻松的技术,该技术使用帕累托最优(Pareto optimality) [34] 来过滤出合适的答案。当没有其他解决方案可以在不减少 y 的情况下增加 x 时,解决方案 (x, y) 是帕累托最优(Pareto optimality)的。同一 Pareto 边界或天际线中的点具有相同的效用。广泛应用于经济学和多目标问题,帕累托最优是没有权重和相似性得分函数的。在实体解析的上下文中,天际线提供了比其他更好的点的选择,但没有量化好多少。指代相同物理空间实体(positive class)的pairs预计具有较高的 δ δ δ 值,因此会形成第一批天际线。假设 δ δ δ 的最佳值属于来自positive class的对,我们将直到第 k k k 个天际线的pairs标记为positive class,其余标记为negative class。据我们所知,我们是第一个提出用于检测实体链接问题匹配的帕累托最优解决方案。
“Definition 2”:如果属性 a a a 的相似性 δ a δ_{a} δa 表示positive class而不是negative class,则属性 a a a 是正区分的。
一个正区分属性的例子是名字的相似性。 较高的名称相似性更有可能表示匹配而不是不匹配。 例如,Mand & Bil 和 Mand og Bil 的名称相似度为 0.75,Solid 和 Sirculus ApS 的名称相似度为 0.16。 因此,前一对比第二对具有更高的匹配概率。 负面区分属性的示例是两个名称之间的编辑距离。 如果名称之间的距离很大,则配对不太可能是匹配的。
“Definition 3”:正判别属性 a a a 的效用,表示为 u a u_{a} ua,是属性相似度 δ a δ_{a} δa 对揭示匹配的贡献,使用帕累托最优性( δ a → 帕累托最优性 u a δ_{a} \stackrel{帕累托最优性}{\rightarrow} u_{a} δa→帕累托最优性ua)。
每个属性相似性都有助于标记问题。 直观地说, a a a 的较高相似度 δ a δ_{a} δa 比 δ a δ_{a} δa 的较低值具有更高的效用。 因此,如果 δ a ( < s 1 , s 2 > ) > δ a ( < s 3 , s 4 > ) δ_{a}(<s_{1}, s_{2}>) > δ_{a}(<s_{3}, s_{4}>) δa(<s1,s2>)>δa(<s3,s4>),则 u a ( < s 1 , s 2 > ) > u a ( < s 3 , s 4 > ) u_{a}(<s_{1}, s_{2}>) > u_{a}(<s_{3}, s_{4}>) ua(<s1,s2>)>ua(<s3,s4>)。
“Definition 4”:表示为 u ( < s i , s j > ) u(<s_{i}, s_{j}>) u(<si,sj>) 的一对pairs的效用是每个属性的效用之和。 u ( < s i , s j > ) = ∑ i = 1 n u a i u(<s_{i}, s_{j}>) = \sum_{i=1}^nu_{a_{i}} u(<si,sj>)=∑i=1nuai。
请注意,一对pairs的效用不是属性相似性的总和 u ( < s i , s j > ) ≠ ∑ i = 1 n δ a i u(<s_{i}, s_{j}>) ≠\sum_{i=1}^nδ_{a_{i}} u(<si,sj>)=∑i=1nδai,而是它们的效用总和 u ( < s i , s j > ) = ∑ i = 1 n u a i u(<s_{i}, s_{j}>) = \sum_{i=1}^nu_{a_{i}} u(<si,sj>)=∑i=1nuai。 然而, u ( < s i , s j > ) = ∑ i = 1 n u a i = ∑ i = 1 n δ a i u(<s_{i}, s_{j}>) = \sum_{i=1}^nu_{a_{i}}=\sum_{i=1}^nδ_{a_{i}} u(<si,sj>)=∑i=1nuai=∑i=1nδai是一种特殊情况。
“Definition 5”:第 k k k 层的天际线 S k y l i n e ( k ) Skyline(k) Skyline(k) 是具有相同效用的pairs < s i , s j > <s_{i}, s_{j} > <si,sj> 的集合,使得 u S k y l i n e ( k ) > u S k y l i n e ( k + 1 ) u_{Skyline(k)} > u_{Skyline(k+1)} uSkyline(k)>uSkyline(k+1)。
显然,
S
k
y
l
i
n
e
(
1
)
Skyline(1)
Skyline(1) 是具有最佳
δ
a
δ_{a}
δa 值的帕累托最优边界。为了继续 Skyline(2),Skyline(1) 的点被移除,边界重新计算。每次我们探索级别
k
k
k 时,
S
k
y
l
i
n
e
(
k
)
Skyline(k)
Skyline(k) 中的值都是具有最高效用的值。这意味着在较低级别中没有其他点可以为positive class带来更高的效用。这个过程一直持续到所有pairs根据它们的天际线进行排名。算法 2 形式化了我们提出的用于对pairs进行排名的程序 Skyline Ranking (SkyRank)。

输入是由 QuadFlex 分块技术产生的一组pairs
P
P
P 和我们将探索的天际线层数
k
k
k。我们发现具有最佳
δ
δ
δ 组合的点支配其余点,因此具有更高的效用(第 3 行)。然后,我们将这些点放入
P
k
P_{k}
Pk 中,保留探索过的天际线并将它们从
P
P
P 中移除(第 5 行)。当所有pairs都被分配到某个天际线时,我们就停止了。
在获得排名后,我们可以假设前几对天际线比其他天际线更有可能指代同一个物理实体。
“Assumption 1”:一个pair被标记为正的概率与其天际线水平成反比。
该假设认为对于 P P P 中的所有 < s i , s j > <s_{i}, s_{j}> <si,sj> 和 < s ′ i , s ′ j > <s′_{i}, s′_{j}> <s′i,s′j> 使得 < s i , s j > <s_{i}, s_{j}> <si,sj> ∈ S k y l i n e ( k ) Skyline(k) Skyline(k), < s ′ i , s ′ j > <s′_{i}, s′_{j}> <s′i,s′j> ∈ S k y l i n e ( k ′ ) Skyline(k' ) Skyline(k′) 并且 k < k ′ k < k′ k<k′,则 < s i , s j > <s_{i}, s_{j}> <si,sj> 比 < s ′ i , s ′ j > <s′_{i}, s′_{j}> <s′i,s′j> 更有可能是匹配的。
ESTIMATING K 估计K
在本节中,我们估计将positive class与negative class分开的天际线水平 k。 我们介绍了两种不同的方法来固定 k 的值:基于阈值的(SkyEx-F 和 SkyEx-FES) 和 无监督的(SkyEx-D)。
SkyEx-F and SkyEx-FES
与实体解析问题[12,13,18]中使用的基于阈值的方法相比,我们必须为属性的每个相似性找到一个阈值,然后为聚合相似性分数的相似性函数找到一个阈值,我们简化了我们的问题只有一个参数:k。我们需要找到最能区分类的 k 值。作为“好模型”的衡量标准,我们选择使用 F-measure 标准,因为我们的数据往往不平衡 [35-37]。在我们的问题的上下文中,我们将true positives TP 定义为引用相同物理实体并正确标记为positives的pairs;true negatives TN 作为对不同物理实体的引用,并被正确标记为negatives的pairs;false positives FP 作为不指代相同物理实体但被错误标记为positives的pairs;false negatives FN 作为引用相同物理实体但被错误地标记为negatives的pairs。因此,精度为
p
=
T
P
T
P
+
F
P
p = \frac{TP}{TP+FP}
p=TP+FPTP ,召回率为
r
=
T
P
T
P
+
F
N
r =\frac{TP}{TP+FN}
r=TP+FNTP 和
F-measure (
F
1
F_{1}
F1) =
2
×
p
×
r
p
+
r
2\times\frac{p \times r}{p+r}
2×p+rp×r 。

k
k
k 越高,第
k
k
k 个天际线中的一对pairs 越不可能属于positives class(Assumption 1)。 SkyEx-F 探索第一个天际线,并在
k
=
k
f
k = k_{f}
k=kf 的值处停止,从而实现最高 F-measure。为了找到
k
f
k_{f}
kf,我们按照算法 2 对pairs进行排序,但是我们在循环中添加了一些额外的计算(第 6-9 行)并在算法 3 中找到最佳
k
f
k_{f}
kf(第 7 行)。SkyEx-F 计算 F-measure每个天际线
k
k
k,将直到第
k
k
k 个天际线的pairs视为正数,其余视为负数。我们将
F
1
(
k
)
F1(k)
F1(k) 添加到集合
F
F
F 中,它在探索更多天际线的同时跟踪 F-measure 的演变。我们发现
k
f
k_{f}
kf 是在 F 中实现最高
F
F
F 度量的
k
k
k 值。从天际线的第一层到
k
f
k_{f}
kf 水平的对被标记为正数,其余的被标记为负数。请注意,SkyEx-F 会探索所有的天际线,然后找到阈值
k
f
k_{f}
kf 。但是,我们可以通过在遍历完整数据集 P 之前在
k
f
k_{f}
kf处停止来优化算法 3。让我们强调一下
p
p
p 和
r
r
r 的一些性质。
Property 1. 召回率是关于天际线数量
k
k
k 的单调非递减函数。
Proof:
k
k
k 条天际线后的召回率是
r
(
k
)
=
T
P
(
k
)
T
P
(
k
)
+
F
N
(
k
)
r (k) = \frac{TP(k)}{TP(k)+FN(k)}
r(k)=TP(k)+FN(k)TP(k) 。 当我们移动到下一个
k
+
1
t
h
k + 1^{th}
k+1th 天际线时,我们将更多对标记为正数,因此找到真正数 TP 的概率更高。 因此,
T
P
(
k
+
1
)
≥
T
P
(
k
)
TP(k+1) ≥ TP(k)
TP(k+1)≥TP(k)。 至于分母,无论天际线水平到了哪里,它总是相同的,因为true positives固定在
P
P
P 中且与我们的labeling无关。 这意味着如果我们发现更多的true positives(TP),那么我们会自动减少false negatives(FN)。 因此,
T
P
(
k
+
1
)
+
F
N
(
k
+
1
)
=
T
P
(
k
)
+
F
N
(
k
)
TP(k+1) + FN(k+1) = TP(k) + FN(k)
TP(k+1)+FN(k+1)=TP(k)+FN(k)。 然后我们可以证明
T
P
(
k
+
1
)
T
P
(
k
+
1
)
+
F
N
(
k
+
1
)
≥
T
P
(
k
)
T
P
(
k
)
+
F
N
(
k
)
\frac{TP(k+1)} {TP(k+1)+FN(k+1)} ≥ \frac{TP(k)}{TP(k)+FN(k)}
TP(k+1)+FN(k+1)TP(k+1)≥TP(k)+FN(k)TP(k) 所以
r
(
k
+
1
)
≥
r
(
k
)
r (k+1) ≥ r (k)
r(k+1)≥r(k) .
Property 2: 根据Assumption 1,精度是关于天际线数量
k
k
k 的单调非递增函数。
精度为
T
P
T
P
+
F
P
\frac{TP}{TP+FP}
TP+FPTP 。 然而,
T
P
+
F
P
TP + FP
TP+FP 是我们的算法标记为positive的,这意味着
T
P
+
F
P
TP + FP
TP+FP是所有属于天际线(直到第
k
k
k 级)的pairs。 根据Assumption 1,当
k
k
k值增加时,
F
P
FP
FP 以比
T
P
TP
TP 更高的速率增加。 可以在 [38] 中找到考虑其相关性(如我们的天际线)对结果进行排名的系统的单调递减精度证明。
Theorem 1: 关于天际线数量
k
k
k 的 F-measure 函数一直在增加,直到一个点或间隔,之后就不能再增加了。
Proof:让我们假设在深入天际线时,我们发现了一个峰值点
k
k
k 或峰值间隔
[
k
i
,
k
j
]
[k_{i}, k_{j}]
[ki,kj],其中
F
1
(
k
)
F1(k)
F1(k) 作为相应的 F-measure。请注意,对于峰值间隔,F-measure是恒定的。由于
F
1
(
k
)
F1(k)
F1(k) 属于一个峰值点/区间,因此在
k
k
k 之后存在一个
F
1
(
k
+
ϵ
)
F 1(k +\epsilon)
F1(k+ϵ) 天际线,使得
F
1
(
k
+
ϵ
)
<
F
1
(
k
)
F 1(k +\epsilon)< F 1(k)
F1(k+ϵ)<F1(k) 。现在,让我们假设我们可以在
k
+
δ
k+δ
k+δ 中找到另一个最优值,使得
F
1
(
k
+
δ
)
>
F
1
(
k
)
F 1(k + δ) > F 1(k)
F1(k+δ)>F1(k)。由于
F
1
(
k
+
ϵ
)
<
F
1
(
k
)
F 1(k +\epsilon)< F 1(k)
F1(k+ϵ)<F1(k),因此
F
1
(
k
+
δ
)
>
F
1
(
k
)
>
F
1
(
k
+
ϵ
)
F 1(k + δ) > F 1(k) > F 1(k +\epsilon )
F1(k+δ)>F1(k)>F1(k+ϵ)。 F1
=
2
p
×
r
p
+
r
= 2\frac{p \times r}{p+r}
=2p+rp×r 可以重写为 F1=
2
1
p
+
1
r
\frac{2}{\frac{1}{p}+\frac{1}{r}}
p1+r12。所以,我们可以重写:
2
1
p
(
k
+
δ
)
+
1
r
(
k
+
δ
)
\frac{2}{\frac{1}{p(k+δ)}+\frac{1}{r(k+δ)}}
p(k+δ)1+r(k+δ)12 >
2
1
p
(
k
)
+
1
r
(
k
)
\frac{2}{\frac{1}{p(k)}+\frac{1}{r(k)}}
p(k)1+r(k)12 >
2
1
p
(
k
+
ϵ
)
+
1
r
(
k
+
ϵ
)
\frac{2}{\frac{1}{p(k+\epsilon)}+\frac{1}{r(k+\epsilon)}}
p(k+ϵ)1+r(k+ϵ)12 ,根据Property 2,
p
(
k
+
δ
)
≤
p
(
k
+
ϵ
)
p(k + δ) ≤ p(k+ \epsilon)
p(k+δ)≤p(k+ϵ),因此:
2
1
p
(
k
+
ϵ
)
+
1
r
(
k
+
ϵ
)
\frac{2}{\frac{1}{p(k+\epsilon)}+\frac{1}{r(k+\epsilon)}}
p(k+ϵ)1+r(k+ϵ)12>
2
1
p
(
k
+
δ
)
+
1
r
(
k
+
ϵ
)
\frac{2}{\frac{1}{p(k+δ)}+\frac{1}{r(k+\epsilon)}}
p(k+δ)1+r(k+ϵ)12,这意味着:
2
1
p
(
k
+
δ
)
+
1
r
(
k
+
δ
)
\frac{2}{\frac{1}{p(k+δ)}+\frac{1}{r(k+δ)}}
p(k+δ)1+r(k+δ)12 >
2
1
p
(
k
+
δ
)
+
1
r
(
k
+
ϵ
)
\frac{2}{\frac{1}{p(k+δ)}+\frac{1}{r(k+\epsilon)}}
p(k+δ)1+r(k+ϵ)12。根据性质 1,这个不等式不能成立,因为
r
(
k
+
δ
)
≥
r
(
k
+
ϵ
)
r(k + δ) ≥ r(k + \epsilon)
r(k+δ)≥r(k+ϵ)。因此,我们对
F
1
(
k
+
δ
)
>
F
1
(
k
)
F 1(k + δ) > F 1(k)
F1(k+δ)>F1(k) 的假设不能成立,并且
F
1
(
k
)
F1(k)
F1(k) 仍然是 F-measure 的最高值。

Theorem 1 确保一旦我们在 F-measure 函数中找到峰值,我们就可以停止寻找所有的天际线并相应地标记这些pairs。 因此,我们可以让算法 3 提前停止。 算法 3 的修改反映在算法 3a 中。 我们使用与算法 3 中相同的程序,但我们不需要跟踪每个天际线及其相应的 F-measure。 相反,我们只在
F
p
r
e
v
i
o
u
s
F_{previous}
Fprevious 中保留之前的 F-measure。 在移动到下一个天际线时,我们计算 F-measure,当我们第一次注意到下降时(第 9 行),我们停止循环(第 10 行)并返回由当前
k
k
k 分隔的两个类(第 7-8 行)。 否则,我们将
F
p
r
e
v
i
o
u
s
F_{previous}
Fprevious 更新为当前 F-measure(第 12 行)并继续搜索最优
k
k
k。
SkyEx-D
前几节中描述的方法假设存在pairs的标签。在本节中,我们假设没有关于标签的信息,因此,我们提出了一种用于固定 k k k 值的启发式方法。启发式是基于positive class和negative class之间的距离。我们将 SkyEx-D 发现的 k k k 称为基于距离的 k k k 或 k d k_{d} kd。我们的类不以小的类内距离为特征。各种模式可以揭示一个positive class;例如,名称相似但类别不同或类别相似且地址相似等。因此,位于第一天际线中的positive class是分散的,不一定形成集群。但是,考虑到与negative class的距离,它们仍然可以与其他部分分开。从理论上讲,当我们在第一个天际线(潜在的积极因素)时,类间距离保持很小,然后在我们进入后来的天际线时开始增加,最后在我们进入更深的天际线时再次下降(潜在的消极因素)。 SkyEx-D 注意到类间距离的增加并相应地设置 k d k_{d} kd。为了获得类间距离的近似值,我们使用均值并将其表示为 μ d μ_{d} μd:
μ
d
=
∑
d
(
p
k
,
p
−
k
)
∣
P
k
∣
\mu_{d}=\frac{\sum d(p^{k},p^{-k})}{|P_{k}|}
μd=∣Pk∣∑d(pk,p−k)
where
∣
P
k
∣
|P_{k}|
∣Pk∣ is the number of pairs from the
1
s
t
1^{st}
1st to the
k
t
h
k^{th}
kth skyline ,
p
k
p^{k}
pk is a pair in
P
k
P^{k}
Pk ,
p
−
k
p^{-k}
p−k is a pair in
P
−
P
k
P-P^{k}
P−Pk , and
d
(
p
k
,
p
−
k
)
d(p^{k},p^{-k})
d(pk,p−k) is the distance between
p
k
p^{k}
pk and
p
−
k
p^{-k}
p−k.
为了修复 k d k_{d} kd,我们在深入天际线的同时监控 μ d μ_{d} μd 的值。 我们用 μ d ( k ) μ_{d}(k) μd(k) 表示 μ d μ_{d} μd 关于 k k k 的函数。 我们使用 μ d ( k ) μ_{d}(k) μd(k) 的一阶导数,表示为 μ d ′ ( k ) μ' _{d}(k) μd′(k),来找到 μ d ( k ) μ_{d}(k) μd(k) 函数减小的点。 这种方法背后的直觉是,在开始时,距离 μ d ( k ) μ_{d}(k) μd(k) 开始增加,这意味着一阶导数具有正斜率( μ d ′ ( k ) > 0 μ' _{d}(k)>0 μd′(k)>0)。 之后,我们进入“灰色区域”,这里既有潜在的积极因素,也有潜在的负面因素。 这是我们需要停止的地方,因为如果我们继续前进,我们可能会失去精确度。 为了找到“灰色区域”,我们注意一阶导数何时将其斜率变为负值。 为了计算 μ d ′ ( k ) μ' _{d}(k) μd′(k),我们估计每个点 k k k 中 μ d ′ ( k ) μ' _{d}(k) μd′(k)的值:
μ d ′ ( k ) = ∂ ∂ k ≈ μ d ( k + 1 ) − μ d ( k ) 1 μ' _{d}(k)=\frac{\partial}{\partial k}≈\frac{μ_{d}(k+1)-μ_{d}(k)}{1} μd′(k)=∂k∂≈1μd(k+1)−μd(k)

为了对 μ d ′ ( k ) μ' _{d}(k) μd′(k) 的小波动不敏感,我们使用高斯函数 1 σ 2 π e − ( x − μ ) 2 / 2 σ 2 \frac{1}{\sigma \sqrt{2\pi}}e^{-(x-\mu)^{2}/2\sigma^{2}} σ2π1e−(x−μ)2/2σ2使用小窗口稍微平滑 μ d ′ ( k ) μ' _{d}(k) μd′(k)。 然后我们监控 μ d ′ ( k ) μ' _{d}(k) μd′(k) 何时第一次减小并相应地设置 k d k_{d} kd。 我们修改算法 2 以适应这种方法。 我们计算第 7 行中 k k k 的每个点的 μ d ′ ( k ) μ' _{d}(k) μd′(k)。然后,我们必须找到平滑后的 μ d ′ ( k ) μ' _{d}(k) μd′(k) 的第一个负值(第 9 行)并相应地固定 k d k_{d} kd(第 10 行)。 最后,我们返回第 16-17 行中 k d k_{d} kd 定义的类。
Summary
算法 4 估计最能区分positive class和negative class的天际线水平 k k k。与使用启发式方法估计其参数的聚类技术类似,SkyEx-D 使用positive class与其他类的距离作为类可分离性的指标。然而,与侧重于集群稳健性的集群指标相比,这不是 SkyEx-* 系列算法的要求。positive pair不显示相似的模式,而是相似的效用,可以更好地被天际线捕捉(见第 9.9 节)。实验表明,我们的类间距离方法估计 k d k_{d} kd 非常接近 k f k_{f} kf 而不会丢失 F-measure。与使用评分函数的技术相比,SkyEx-* 系列算法抽象了效用的概念。因此,不需要权重或相似度函数。尽管positive class可以通过各种属性相似性模式来表征,SkyEx-* 系列算法仍然可以基于高效用将positive class组合在一起,而聚类技术将重点放在分别对每个模式进行分组,而不是将positive class pairs在一起成为一个集群。此外,SkyEx-* 系列算法的灵活性使其适用于缺少有关属性贡献的专家知识的所有问题。最后,SkyEx-* 系列算法不学习任何行为,因此不存在过度拟合的风险。
COMPLEXITY ANALYSIS OF QUADSKY
在本节中,我们将讨论我们的算法和我们的QuadSky解决方案的时间复杂性。
QuadFlex
QuadFlex处理的是点(而不是区域);因此,它的行为类似于点状四叉树。QuadFlex的拆分方式与四叉树相同,但与四叉树不同的是,点可以被分配给一个以上的孩子。我们构建QuadFlex结构只是为了形成区块。因此,我们对构造的复杂性感兴趣。让我们用 ∣ S ∣ |S| ∣S∣表示 S S S中的点的数量, c c c表示任何两个点之间的最小距离, D 1 D_{1} D1和 D 2 D_{2} D2表示包含所有点的初始区域的尺寸。让我们首先估计一下QuadFlex的深度。QuadFlex中任何两个点 p 1 p_{1} p1和 p 2 p_{2} p2的距离 c c c总是小于它们所属节点的对角线。鉴于QuadFlex允许相邻的点包含在一个以上的子节点中,这个计算需要修改。初始( 0 0 0级)节点的物理对角线是 D 1 2 + D 2 2 \sqrt{D_{1}^{2}+D_{2}^{2}} D12+D22。第 i i i级的对角线是 D 1 2 + D 2 2 4 i \frac{\sqrt{D_{1}^{2}+D_{2}^{2}}}{4^{i}} 4iD12+D22。为了修改计算结果,我们估算一下,如果QuadFlex会在物理上扩展以容纳相邻的点,那么: c ≤ 3 D 1 2 2 + 3 D 2 2 2 4 i c≤ \frac{\sqrt{\frac{3D_{1}^{2}}{2}+\frac{3D_{2}^{2}}{2}}}{4^{i}} c≤4i23D12+23D22 现在,把 i i i从这个方程中分离出来,结果是 i ≤ l o g 4 3 2 ( D 1 2 + D 2 2 ) c = l o g 4 3 2 + l o g 4 D 1 2 + D 2 2 c i≤ log_{4}\frac{\sqrt{\frac{3}{2}(D_{1}^{2}+D_{2}^{2})}}{c} = log_{4}\sqrt{\frac{3}{2}} + log_{4}\frac{\sqrt{D_{1}^{2}+D_{2}^{2}}}{c} i≤log4c23(D12+D22)=log423+log4cD12+D22。 l o g 4 3 2 ≈ 0.14 log_{4}\sqrt{\frac{3}{2}}≈0.14 log423≈0.14,所以我们可以放弃它(少于一个级别): i ≤ l o g 4 D 1 2 + D 2 2 c i≤ log_{4}\frac{\sqrt{D_{1}^{2}+D_{2}^{2}}}{c} i≤log4cD12+D22。为了估计最大深度,我们需要增加一个层次(根),所以深度估计为 l o g 4 D 1 2 + D 2 2 c + 1 log_{4}\frac{\sqrt{D_{1}^{2}+D_{2}^{2}}}{c}+1 log4cD12+D22+1。最后,对于构建QuadFlex,复杂度为 O ( ∣ S ∣ ( l o g 4 D 1 2 + D 2 2 c + 1 ) ) O(|S|(log_{4}\frac{\sqrt{D_{1}^{2}+D_{2}^{2}}}{c} + 1)) O(∣S∣(log4cD12+D22+1))。
SkyRank
SkyRank需要计算Pareto边界,这很耗时。在典型的情况下,从QuadFlex产生的对 P P P在所有 d d d维度上进行比较,其时间复杂度为 O ( 2 ∣ P ∣ d ) O(2^{|P|^{d}}) O(2∣P∣d),这是不可以扩展的。SkyRank使用了[40]中提出的方法,该方法首先缩小了 d d d维领域的规模,然后使用网格对数据进行预过滤。这使得第一条天际线的时间复杂度为 O ( ∣ P ∣ 2 ) O(|P|^{2}) O(∣P∣2)。对于总数为K的天际线,其复杂度为 O ( K ∣ P ∣ 2 ) O(K|P|^{2}) O(K∣P∣2)。
SkyEx-F
SkyEx-F在将下一个天际线添加到正类的同时计算这些指标;因此,这些计算并没有增加任何复杂性。最后,我们对 F F F进行线性搜索,找到具有最高 F F F度量的天际线。 F F F的大小是等于 K K K,所以复杂度为 O ( K ∣ P ∣ 2 + K ) O(K|P|^{2}+K) O(K∣P∣2+K)。
SkyEx-FES
SkyEx-FES比SkyEx-F更早停止,避免了很大一部分耗时的Pareto计算。考虑到最佳配对通常集中在第一条天际线上,截止时间为 k << K k<<K k<<K。此外,根据定理1,我们不需要存储F ,所以我们避免了对最佳F-measure的线性搜索。其复杂性为 O ( k ∣ P ∣ 2 ) O(k|P|^{2}) O(k∣P∣2)。
SkyEx-D
SkyEx-D使用所有 K K K个帕累托计算,然后,为了估计截止线 k d k_{d} kd,它计算正类和其他类之间的距离。SkyEx-D创建了一个矩阵,其中行是正类 P + P^{+} P+,列是负类数据点 ∣ P ∣ − P + |P|-P^{+} ∣P∣−P+,所以复杂性是 P + ∗ ( ∣ P ∣ − P + ) P^{+}∗ (|P|-P^{+}) P+∗(∣P∣−P+)。 P + ∗ ( ∣ P ∣ − P + ) = P + ∗ ∣ P ∣ − ( P + ) 2 P^{+}∗ (|P|-P^{+})= P^{+} ∗ |P| - (P^{+})^{2} P+∗(∣P∣−P+)=P+∗∣P∣−(P+)2是一条垂直抛物线的方程,它向下开口为 − a x 2 + b x + c -ax^{2} + bx + c −ax2+bx+c,最大值在顶点 ( − b 2 a ) (-\frac{b}{2a}) (−2ab)。在我们的例子中, P + ∗ ( ∣ P ∣ − P + ) P^{+}∗ (|P|-P^{+}) P+∗(∣P∣−P+)的最大值在 ∣ P ∣ 2 \frac{|P|}{2} 2∣P∣,导致最大复杂度为 ∣ P ∣ 2 4 \frac{|P|^{2}}{4} 4∣P∣2。对于 K K K中的每个天际线 k k k,最大复杂度为 ∣ P ∣ 2 4 \frac{|P|^{2}}{4} 4∣P∣2,因此, K ∣ P ∣ 2 4 K\frac{|P|^{2}}{4} K4∣P∣2为所有。注意这里 K << P K<<P K<<P,所以它远不是一个三次方的复杂性。SkyEx-D计算每个 k k k的平均距离 μ d μ_{d} μd,这已经可以在 ∣ P ∣ 2 4 \frac{|P|^{2}}{4} 4∣P∣2的复杂性内完成。然后,我们计算均值的导数 μ ′ d μ′_{d} μ′d,这在 K K K中具有线性复杂度。最后,我们需要再进行一次部分扫描,直到导数 μ ′ d μ′_{d} μ′d第一次变成负数的 k d ( k d << K ) k_{d}(k_{d}<<K) kd(kd<<K)。因此,总复杂度为 O ( K ∣ P ∣ 2 + K ∣ P ∣ 2 4 + K + k d ) = O ( 5 K 4 ∣ P ∣ + K + k d ) O(K|P|^{2} +K\frac{|P|^{2}}{4} +K +k_{d}) = O(\frac{5K}{4}|P|+K +k_{d}) O(K∣P∣2+K4∣P∣2+K+kd)=O(45K∣P∣+K+kd)。
Summary
QuadFlex的复杂度为 O ( n l o g n ) O(nlogn) O(nlogn),成对比较的复杂度为线性 O ( n ) O(n) O(n),而SkyEx-*系列算法的复杂度为二次 O ( n 2 ) O(n^{2}) O(n2)。然而,如果天际线的数量 K = ∣ P ∣ K=|P| K=∣P∣,SkyEx-F和SkyEx-D存在着理论上的复杂度为三次的风险。这意味着 K K K中的每条天际线只包含一对实体,这在理论上可能发生,但在实践中几乎不会发生。因此,这些算法在平均情况下具有二次复杂度。SkyEx-D的复杂性最高,其次是SkyEx-F和SkyEx-FES。总的来说,QuadSky的复杂度是二次的。
EXPERIMENTS
Dataset Description
在这些实验中使用的空间实体来自四个来源,即Google Places(GP)、Foursquare(FSQ)、Yelp和Krak。Krak(www.krak.dk)是一个基于位置的来源,提供丹麦的公司、企业等信息,也是出版黄页的Eniro Danmark A / S.的一部分。数据是通过使用可用的API和[41]中详述的算法获得的。该数据集由75,541个空间实体组成,其中51.50%来自GP,46.22%来自Krak,0.03%来自FSQ,2.23%来自Yelp(这些空间实体在地图上的分布见补充材料附件A)。该数据集为69MB。对于100米的分块范围,有35,521个空间实体在数据集中至少有一个正面的匹配,从而有27,102对需要被发现。这些对中有7795个是在同一来源中,这表明这些来源中没有一个是没有重复的。3,546个同源链接来自GP,3,789个来自Krak,460个来自Yelp。至于不同来源的链接,所有来源都相互重叠,但重叠度最高的17,405对(90%的不同来源链接)来自于Krak和GP。
QuadFlex Performance
在本节中,我们将QuadFlex的性能与四叉树、固定半径最近的邻居算法[42](FNN)以及完全没有索引(No-Index)进行比较。FNN可以找到距离每个点的固定半径内的邻居。QuadFlex和四叉树算法是用Java实现的,而FNN是使用空间索引在Postgres数据库(https://www.postgresql.org)上运行。GiST(B-树和R-树的优化C实现)和SP-GiST(四叉树和kd树的优化C实现)。我们的数据集包含北丹麦地区的75,541个实体(约16个城镇,7,933平方公里),因此平均密度不高,尽管有些地区的密度很高。高数据密度意味着有更多的数据对可以进行比较。为了在不同的数据密度上测试我们的QuadFlex,我们从奥尔堡(139平方公里)模拟了多达1,000,000个随机点。
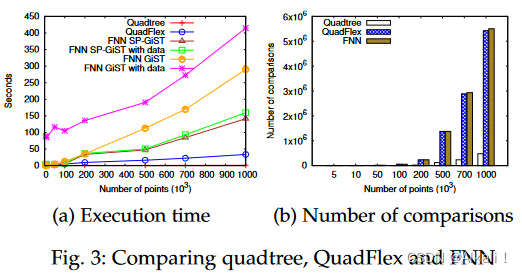
图3显示了quadtree、QuadFlex和FNN在执行时间(图3a)和比较次数(图3b)方面的比较。带有数据的FNN版本在数据库中计算,然后将数据对加载到java实现中。四叉树的执行时间最低,其次是QuadFlex。FNN SP-GiST与QuadFlex相当,有时甚至在小数据集上比QuadFlex更好。然而,当数据集的大小增加时,QuadFlex保持的执行时间比FNN GiST少8倍,比FNN SPGiST少3倍。在所有的数据集大小上,带有SP-GiST索引的FNN都优于FNN GiST。No-Index的效率非常低,比带数据的FNN Gist慢了848倍,比QuadFlex慢了368,095倍。鉴于No-Index会使其他曲线相形见绌,所以它不是图3a的一部分,而是参考补充材料中的图2,附件B。至于比较的数量,QuadFlex列举的比较数量是quadtree的12倍。此外,QuadFlex几乎包含了FNN的所有(99.99%)比较,而四叉树只包含FNN的10%。此外,考虑到QuadFlex的可扩展性优于FNN,并且QuadFlex独立于数据库的实现,大约0.01%的比较的损失是微不足道的。
SkyEx-F Results
我们以100米和无密度限制的方式运行QuadFlex,我们得到了777,452对(1426MB)。Having the same website or phone is a strong indicator of a match, so we use these attributes to infer the label.We refer to this labeling as automatic labeling.(拥有相同的网站或电话是匹配的有力指标,所以我们使用这些属性来推断标签。我们把这种标签称为自动标签。)然而,可能会出现电话号码或网站不同但仍是同一实体,或电话号码相同但实体不同的情况。因此,我们手动检查了1500对实体的标签样本(1552 kB)。我们将手动检查的标签对的样本称为Dsample,将完整的数据集称为Dfull。在777,452对的完整数据集上手动检查标签是不可行的。因此,我们检查了大约10,000个配对,对于其余的,我们依靠自动标签。SkyEx-F在Dsample和Dfull上的结果见图4和图5。
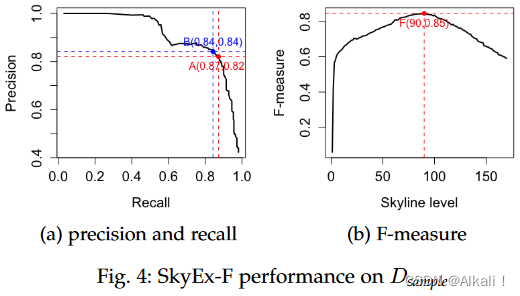
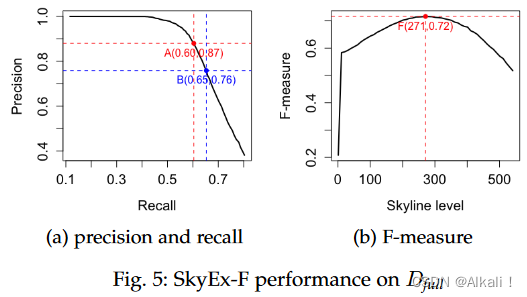
图4a和5a中的曲线显示了当我们从一个天际线移动到下一个天际线时p(y轴)和r(x轴)的演变。我们探索得越多,就越有可能检索到更多的true positive,从而提高r。然而,我们探索得越多,并将配对标记为positive,就越有可能增加false positive的数量,所以p会下降。该算法探索了几种权衡方法;例如,A和B点是最好的。图4a中p为0.87,r为0.82的A点在F-measure方面也是同样的最佳点,所以这就是SkyEx-F将固定
k
f
k_{f}
kf的地方。图4b显示了天际线的水平,以及达到的F-measure值。最高值是0.85,对应于
k
=
90
k=90
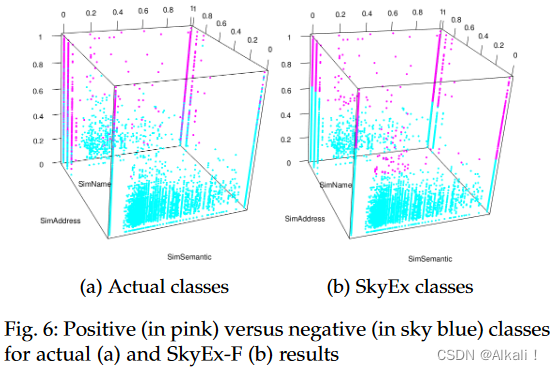
k=90。与样本(F-measure为0.85)相比,对全部数据集的评估得出的数值较低(F-measure为0.72),这可能是自动标签的一个简单结果。A点的R值为0.6,P值为0.87,而B点的R值较高,为0.65,P值较低,为0.76(图5a)。为了了解Dfull和天际线中的真实类,我们在图6中绘制了它们的分布(实际的positive class为粉红色,negative class为天蓝色)。值得注意的是,positive class pairs被分配在维度的最高值。尽管两张图之间存在差异,但SkyEx-F在分离positive class和negative class方面显示出有希望的结果,其r为0.6,p为0.87。
Experimenting with Different QuadFlex Parameters
到目前为止,我们使用QuadFlex分块技术,100米,没有密度限制。在本节中,我们将评估我们的QuadSky方法在不同分块参数下的效果。
Changing m, no density limit
在这个实验中,我们测试了QuadFlex中用于创建空间块的不同m值。我们测试的m值为1、20、40、60、80和100米。他们每个人的数据集的大小在表2中列出。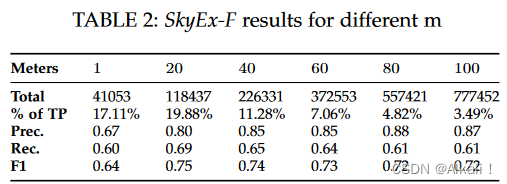
空间上接近的点很可能是一个匹配点。因此,对于较小的m值,true positive的百分比通常较高。一个有趣的情况是m=1,其中true positive(TP)的百分比低于m=20。人们期望相距1米的点毫无疑问会是一个匹配点。然而,情况并非总是如此。购物中心、容纳几家公司的建筑物等都有相同的坐标特征,但不一定是相同的空间实体。表2列出了不同m值的结果(见补充材料附件C中所有截止点的精度-召回图)。在所有情况下,r都高于0.6。对于所有的m值,p都高于0.8,除了m=1,p是0.67。对于m=1,正负两类混合,因此SkyEx在p上有一点损失。这也是反对任意合并相距5米的点的工作的一个论据。空间上的接近并不是一个确定的匹配指标。
Changing d, m ≤ 100.
我们试验了不同的密度值
d
d
d及其对结果的影响。数据集的大小、true positive的百分比以及精度、召回率和F-measure方面的结果见表3(见[14]中图9中所有截止点的精度-召回率图)。
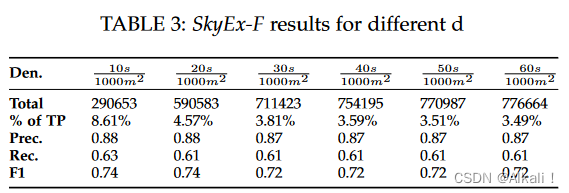
当密度较小时,我们迫使QuadFlex进一步分割并创建更小的块。因此,pairs的数量减少了。请注意,与此相反,true positive(TP)的比例会增加。事实上,进一步拆分使我们能够创建更好的区块,其中包含更高的TP百分比。然而,当密度限制增加到
30
s
1200
m
2
\frac{30s}{1200m^{2}}
1200m230s以上时,越来越少的区块被进一步分割,所以数据集的大小和TP的百分比没有明显变化。在所有情况下,r保持在0.61以上,p保持在0.87以上。在密度为
10
s
1000
m
2
\frac{10s}{1000m^{2}}
1000m210s(最低参数)的情况下,p(0.88)和r(0.63)略好。SkyEx-F在寻找正确的类别方面适应性很强,即使区块的大小发生变化,即使true positive与true negative的比例发生变化。
SkyEx-FES Optimization 优化
鉴于定理1中的理论保证,我们可以按照算法3a中的描述提前停止SkyEx-F。我们对相距30、50、80和100米的空间实体运行SkyExFES。在所有情况下,SkyEx-FES发现的 k f k_{f} kf值与SkyEx-F平均只探索了27%的天际线。关于迭代次数的比较,见表4。对于相距30米、50米、80米和100米的空间实体,SkyEx-FES分别找到了探索36%、27%、23%和22%天际线的最佳 k f k_{f} kf。此外,我们在理论上保证F-测量函数只有一个最佳值,这一点在图4b和5b中也可以注意到。
SkyEx-D Performance
在这些实验中,我们使用 SkyEx-D(算法 4)来设置
k
d
k_{d}
kd 并根据 F-measure 评估我们的结果。我们将 SkyEx-D 应用于相距 30、50、80 和 100 米的空间实体(请参阅表 4 中的数据集详细信息)。我们计算每个点的一阶导数 (
μ
′
d
μ′_{d}
μ′d),如算法 4 所示。关于
k
k
k 的平滑
μ
d
′
(
k
)
μ' _{d}(k)
μd′(k)如图 7 所示。
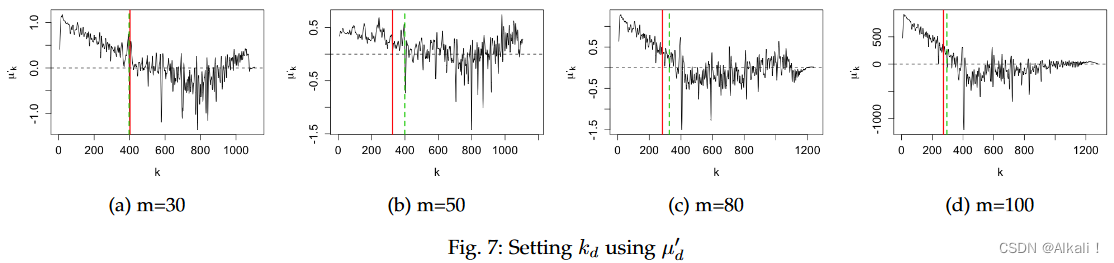
红色实线表示
k
f
k_{f}
kf 的值,而绿色实线表示虚线表示 SkyEx-D 发现的
k
d
k_{d}
kd。我们注意到当
μ
d
′
(
k
)
μ' _{d}(k)
μd′(k) 第一次为负时并相应地设置
k
d
k_{d}
kd。对于相距 30 m 的空间实体(图
7
a
7_{a}
7a),
k
d
k_{d}
kd 与
k
f
k_{f}
kf 仅相距 5 条天际线,但 50 m 有 73 条天际线。这些
k
d
k_{d}
kd值是使用一阶导数发现的。我们在增加
k
k
k 的同时说明
μ
k
μ_{k}
μk 的趋势,这意味着我们探索更深的天际线并检查更多不太可能匹配的对。从正类到负类的距离在开始时较小,因为均值
μ
k
μ_{k}
μk 受到接近点的影响。当我们增加
k
k
k 时,
μ
k
μ_{k}
μk 增加,这意味着类别之间变得越来越可区分。
μ
k
μ_{k}
μk 的高值表明类之间的距离很大。对于相距 80 m 和 100 m 的空间实体,
μ
k
μ_{k}
μk 开始比相距 30 m 和 50 m 的空间实体下降得更快(图 8)。
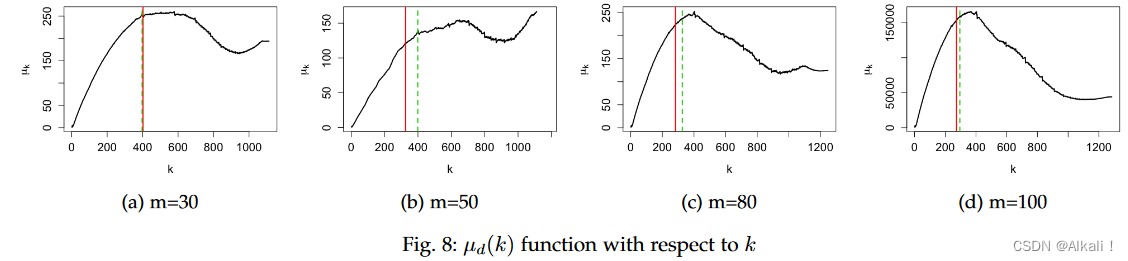
这一观察可以通过以下事实得到证明:邻近的实体更难分类,因此潜在截止点的“灰色”区域更大。然而,SkyEx-D 从一阶导数中检测到
μ
k
μ_{k}
μk 的第一次减少并固定
k
d
k_{d}
kd。从图形上看,这一点与“灰色”区域的开始重合。尽管
k
d
k_{d}
kd有时远离
k
f
k_{f}
kf (m=50),但相应的 Fmeasures 几乎相同(图 9)。图 9 中的红线对应于
k
f
k_{f}
kf,绿线对应于
k
d
k_{d}
kd。
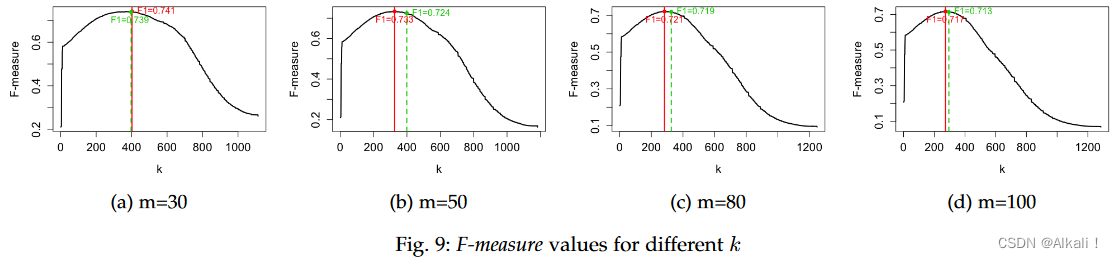
F 度量的差异为 30 m 为 0.002,50 m 为 0.009,80 m 为 0.002,100 m 为 0.004。因此,使用 k d k_{d} kd 而不是 k f k_{f} kf 对pairs进行分类的 F 度量差异始终小于 0.01。这意味着我们的 SkyEx-D 尽管完全没有监督,但在 F 度量方面几乎是最优的。在精度、召回率和 F-measure 方面,[14] 中带有 SkyEx 的 QuadSky、带有 SkyEx-F 的 QuadSky 和带有 SkyEx-FES 的 QuadSky 报告了相同的值。但是,底层算法不同。 [SSTD2019@Multi-Source Spatial Entity Linkage] 中的 SkyEx 需要阈值 k k k 来分隔天际线,而对于 SkyEx-F 和 SkyEx-FES,不需要指定 k k k 因为算法将通过天际线探索来修复它(SkyEx-FES 只有 30% 的天际线)。带有 SkyEx-D 的 QuadSky 完全不受监督,可能会产生不同的结果。最佳方案是将 k d k_{d} kd 固定为 k f k_{f} kf 。
Comparison With Baselines
尽管在空间数据整合方面有多篇论文,但[11]、[12]、[13]的工作与我们的工作最为相似,因为其余的相关工作只考虑空间对象,而不是空间实体,或者使用监督学习技术。我们将把QuadSky与Berjawi等人[12]、Morana等人[13]、Karam等人[11]进行比较。
- Berjawi等人[12]对地理坐标提出了欧氏距离,对所有其他属性提出了Levenshtein相似度。这些相似性加在一起就是一个全局相似性。论文中提到的属性是姓名和电话。然而,由于电话是我们自动标签的一部分,它不能在算法中也使用。作者认为 s c o r e ≥ 0.75 score≥0.75 score≥0.75的匹配是高置信度的匹配。我们使用这个阈值,但也尝试其他可能产生更好结果的阈值(带有后缀-Flex的版本)。我们与作者提出的两个版本进行比较:姓名+地址+地理坐标(V1)和姓名+地理坐标(V2)。
- Morana等人[13]建议过滤那些在名称中共享相同类别或标记的实体。然后用欧氏距离比较这些实体的坐标,用Levenshtein比较地址和名称,用Resnik相似度(Wordnet)比较类别。像地址、电话等属性被认为是次要的,所以它们在相似性评分函数中被赋予 1 3 \frac{1}{3} 31的权重,而名称、类别和地理上的接近性则被赋予 2 3 \frac{2}{3} 32的权重。作者展示了每个实体的前 k k k个匹配的实体,供用户决定。
- Karam等人[11]首先过滤相距5米的空间实体。然后,用Levenshtein距离测量名称的相似性,用欧氏距离测量地理相似性,并对关键词进行语义比较。为了决定哪些对需要匹配,哪些不需要,使用信念理论[26]对相似性进行融合。使用
D
f
u
l
l
D_{full}
Dfull和
D
s
a
m
p
l
e
D_{sample}
Dsample的结果见表5。
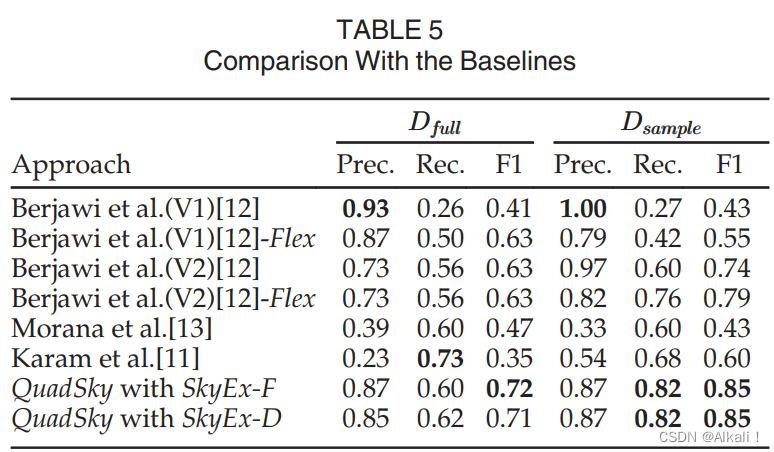
一般来说,由于标签的质量较好,所有的方法在 D s a m p l e D_{sample} Dsample中的表现都比较好。Berjawi等人(V2)[12]产生了合理的结果,是仅次于QuadSky的第二好的方法,在 D f u l l D_{full} Dfull中的F-measure为0.63,在 D s a m p l e D_{sample} Dsample中为0.74。如果我们允许灵活的阈值,Berjawi等人(V2)[12]-Flex在 D f u l l D_{full} Dfull中找到了同样的最佳阈值0.75,而在 D s a m p l e D_{sample} Dsample中,0.65的阈值产生了更好的结果,将Fmeasure从0.74提高到0.79(关于所有的阈值及其结果,见补充材料,附件D)。
为了与Morana等人[13]进行比较,我们尝试了从1到单点最大匹配的所有数值
k
k
k(见[14]中的图10)。Fmeasure的最高值对应于0.39的精确率和0.60的召回率。Morana等人[13]在
D
s
a
m
p
l
e
D_{sample}
Dsample中的行为是类似的;Fmeasure的最佳值是在
k
=
3
k=3
k=3时达到的,结果与
D
f
u
l
l
D_{full}
Dfull中的结果类似。Karam等人[11]的工作在
D
f
u
l
l
D_{full}
Dfull中取得了最高的召回率值0.73,但精确率值很低,为0.23。因此,Fmeasure只有0.47。然而,在
D
s
a
m
p
l
e
D_{sample}
Dsample中,该方法的整体表现更(Fmeasure=0.6)。QuadSky版本在精确率和召回率之间提供了最好的权衡,因此在两个数据集中的Fmeasure也是最高的。在
D
s
a
m
p
l
e
D_{sample}
Dsample中,与所有基线相比,带有SkyEx-F的QuadSky和带有SkyEx-D的QuadSky实现了最佳的召回率。更重要的是,即使使用无监督算法,QuadSky with SkyEx-D仍然比基于阈值的基线好。Berjawi等人(V1)[12]实现了两个数据集的最高精确率值,但召回率很低,模型的整体表现也很差。事实上,达到极端值(高精确度-低召回率或低精确度-高召回率)的模型不是一个可行的解决方案,因为它们要么限制性太强,要么太灵活,而且预测性很差。
Berjawi等人[12] (V2)-Flex假设所有相似性的权重相同,而且报告的精确率和召回率的值也不错。然而,配对的行为可以是各种类型的。QuadSky可以比简单的总和更好地捕捉这些不同的行为。
关于基线的复杂性,我们无法从分块技术方面进行判断,因为没有关于作者是否使用索引来创建分块的细节。然而,正如我们在图3中所示,Postgres中现有的FNN解决方案的规模仍然不如我们的QuadFlex好。因此,我们在分块步骤中的表现更好。
成对比较对所有基线和我们的解决方案都有线性复杂度。
至于标注,基线不需要由我们的天际线引起的二次复杂性。我们的SkyEx-*系列算法在
D
s
a
m
p
l
e
D_{sample}
Dsample中运行了1分钟,在
D
f
u
l
l
D_{full}
Dfull中运行了2小时,有777,452对。然而,实体联系问题是在离线情况下进行的,因此,尽管在一般情况下,快速的解决方案是最好的,但有效性更为重要,在这里,QuadSky明显优于基线。
Comparison With Supervised Learning Techniques
在本节中,我们保留了QuadSky的步骤,但用监督学习技术取代了对实体对的标记。我们决定将SkyEx-*系列算法与逻辑回归、支持向量机(SVM)、决策树和Naive Bayes进行比较,这些是常用于实体解析问题的监督学习技术。我们将这些方法应用于相距最多30米的
D
f
u
l
l
D_{full}
Dfull对(数据集描述见表3)。我们试验了对75%的
D
f
u
l
l
D_{full}
Dfull进行训练,并对剩下的25%进行4倍交叉验证(
D
f
u
l
l
−
D
f
u
l
l
D_{full}-D_{full}
Dfull−Dfull),对75%的
D
s
a
m
p
l
e
D_{sample}
Dsample进行训练,并对剩下的25%进行4倍交叉验证(
D
s
a
m
p
l
e
−
D
s
a
m
p
l
e
D_{sample}-D_{sample}
Dsample−Dsample),以及对
D
s
a
m
p
l
e
D_{sample}
Dsample进行训练,对
D
f
u
l
l
D_{full}
Dfull进行测试(
D
s
a
m
p
l
e
−
D
f
u
l
l
D_{sample}-D_{full}
Dsample−Dfull)。结果见表6。
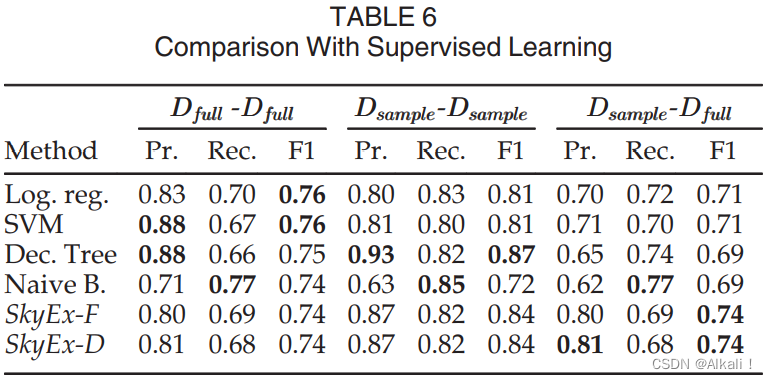
虽然逻辑回归和SVM在
D
f
u
l
l
−
D
f
u
l
l
D_{full}-D_{full}
Dfull−Dfull中产生的F值略高,为0.76,但我们的算法,不在标记的数据上建立模型,在
D
f
u
l
l
−
D
f
u
l
l
D_{full}-D_{full}
Dfull−Dfull中几乎有相同的F值(SkyEx-F和SkyEx-D为0.74)。对于
D
s
a
m
p
l
e
−
D
s
a
m
p
l
e
D_{sample}-D_{sample}
Dsample−Dsample中的人工标注数据集,我们的算法表现第二好(F值为0.84),仅次于决策树。SkyEx-F和SkyEx-D的表现优于逻辑回归、SVM和Naive Bayes,其F值分别为0.81、0.81和0.72。像
D
f
u
l
l
−
D
f
u
l
l
D_{full}-D_{full}
Dfull−Dfull那样拥有一个大的训练集在大多数实际情况下是不现实的。因此,我们尝试了一个更现实的方案,即准备一个小型的人工标注的训练集,然后在完整的数据上测试训练好的模型(
D
s
a
m
p
l
e
−
D
f
u
l
l
D_{sample}-D_{full}
Dsample−Dfull)。在这种(最现实的)情况下,SkyEx-F和SkyEx-D在F-measure上比所有的监督方法都要好0.03-0.05,显示了监督模型的主要弱点,即
D
s
a
m
p
l
e
D_{sample}
Dsample模型在应用于
D
f
u
l
l
D_{full}
Dfull时不够有代表性。一般来说,空间实体解析问题受到缺乏标记数据的困扰。因此,监督学习技术的适用性是有限的。相反,SkyEx-D是完全无监督的,仍然可以取得类似于监督技术的结果。如果有标注的数据,请注意,监督学习技术是在标注的数据上建立模型,而SkyEx-F和SkyEx-FES只使用标注来调整阈值,因为天际线的构建是独立于标注的。由于这个原因,与监督学习相比,SkyEx-F和SkyEx-FES不需要一个大的、有代表性的训练集,不需要纠结于类的不平衡,不需要过度拟合数据,而且其维度最小(一个天际线与高维数据相比)。
Comparison of SkyEx-D to Clustering Techniques
在第7.2节中,我们声称聚类技术将无法创建两个聚类:一个用于正类对,一个用于负类对。在这一节中,我们将用常见的聚类技术取代SkyEx-D,并对所形成的聚类进行评估。我们将与基于距离的聚类(k-means和k-medoids)、层次聚类(agglomerative)和基于密度的聚类(DBSCAN)进行比较。结果列于表7。
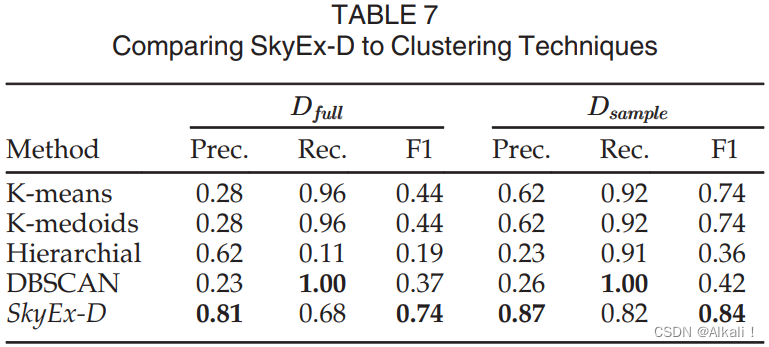
对于k-means和k-medoids,我们指定聚类的数量为2。 对于层次聚类,我们切割树状图以创建两个聚类。对于DBSCAN,我们尝试了几个最小点的值,以形成两个聚类,或者一个聚类和噪声点。我们在表格中报告了带有噪声点的版本,因为它产生了更好的结果。对于标签,我们尝试了两个版本(将聚类1标记为正数,其余为负数,反之亦然),并在表中报告了最佳版本。基于距离的聚类产生了最好的结果,具有最高的召回率,但是在
D
f
u
l
l
D_{full}
Dfull中的精度很低,只有0.28,在
D
s
a
m
p
l
e
D_{sample}
Dsample中的
F
−
m
e
a
s
u
r
e
F-measure
F−measure为0.74,是第二好的(在SkyEx-D之后)。分层聚类比基于距离的聚类取得了更高的精度,但在
D
f
u
l
l
D_{full}
Dfull中的召回率非常低,只有0.11,而结果却相反,在
D
s
a
m
p
l
e
D_{sample}
Dsample中的召回率高,为0.91,精度低,为0.23。对于DBSCAN,当我们将聚类标记为负数,而将噪声点标记为正数时,取得了最好的数值,结果是召回率为1.0,但在
D
f
u
l
l
D_{full}
Dfull中的精度非常低,为0.23,在
D
s
a
m
p
l
e
D_{sample}
Dsample中为0.26。这意味着正类对的密度不足以形成一个集群。我们的SkyEx-D更注重类之间的距离,而不是类内的距离,因此表现优于聚类。
CONCLUSIONS AND FUTURE WORK
基于位置的数据源提供了关于空间实体的丰富细节和语义。然而,识别哪些空间实体对是指同一物理实体是一个具有挑战性的问题。在本文中,我们解决了跨多个基于位置的来源的空间实体解析问题。我们提出了QuadSky,一种由空间分块技术QuadFlex、每个属性的适当相似度量的成对比较、基于天际线的排名算法SkyRank和用于分类配对的SkyEx-*系列算法组成的方法。
- QuadFlex将空间实体排列成空间块,执行时间短(比FNN少4-8倍),并且没有遗漏相关的比较(FNN比较的99.99%)。
- SkyEx-F在人工标注的数据集上达到 0.84 0.84 0.84的精确率和 0.84 0.84 0.84的召回率,在自动标注的数据集上达到 0.87 0.87 0.87的精确率和 0.6 0.6 0.6的召回率。我们提供了理论上的保证,用新颖的SkyEx-FES修剪SkyEx-F中73%的天际线探索而不损失任何F值。
- 我们完全无监督的SkyEx-D发现 k d k_{d} kd非常接近最佳 k f k_{f} kf(F-measure损失仅为0.01)。
SkyEx-*系列算法在F-measure方面优于现有的基线,并且在不需要标记数据集的情况下接近于监督学习解决方案的结果,而SkyEx-D产生的结果远远好于聚类技术。
SkyEx-F和SkyEx-D已经在R skyex包中提供,还有其他用于实体解析的函数。在未来的工作中,我们的目标是研究结合几个属性的不同分块技术,并将我们的SkyEx-*系列算法扩展到一般的(非空间)实体解析问题。
代码解析
源码参考:skyex-package
Blocking 分块
textual_blocking 以文本相似性作为分块标准分块
#' @title Textual blocking
#' @description Creates blocks of entities that have textual similarity. Returns the pairs 创建有文本相似性的实体的块 返回一对对具有文本相似性的对pairs
#'
#' @param data A dataframe of entities 实体的数据框
#' @param column The column name of the attribute that will be considered for blocking 将被作为分块依据的实体属性的列名
#' @param label Method for textual blocking; choose among levenshtein, cosine, jaccard, jarowinker, qgram
#' @param max_distance The maximal distance allowed in a block 块内所允许的最大距离
#'
#' @return blocks A dataframe of pairs 返回存储pairs的数据框
#'
#' @export
function (data, column, method, max_distance)
{
blocks <- NULL
data$row <- rownames(data) #给data数据增加一列,为行的序号
if (is.null(column)) {
stop("select the column for textual blocking") #请选择文本分块的列
}
if (is.na(match(column, names(data)))) { #拿列名column去和数据集中的列名去匹配
stop("enter a valid column name") #请输入有效的列名
}
if (is.null(method)) {
stop("select a method: levenshtein, cosine, jaccard, jarowinker, qgram")
#请选择一个方法
}
if (is.null(max_distance)) {
stop("set max_distance to the maximal distance allowed for the selected column")
#将 max_distance 设置为所选列允许的最大距离
}
# stringdist_inner_join:根据列的模糊字符串匹配连接两个表
# stringdist_join(
# x, #A tbl
# y, #A tbl
# by = column, #Columns by which to join the two tables
# max_dist = 2, #Maximum distance to use for joining
# method = c("osa", "lv", "dl", "hamming", "lcs", "qgram", "cosine", #"jaccard", "jw", "soundex"), #计算字符串距离的方法,见 stringdist 包中的stringdist-metrics
# mode = "inner", #连接方式
# ignore_case = FALSE, #是否不区分大小写(默认是)
# distance_col = NULL, #如果给定,将添加一个具有此名称的列,其中包含传递给 stringdist 的两个参数之间的差异
# ...
#)
switch(method, levenshtein = {
blocks <- stringdist_inner_join(data, data, by = column,
method = "lv", max_dist = max_distance, ignore_case = TRUE)
}, cosine = {
blocks <- stringdist_inner_join(data, data, by = column,
method = "cosine", max_dist = max_distance, ignore_case = TRUE)
}, jaccard = {
blocks <- stringdist_inner_join(data, data, by = column,
method = "jaccard", max_dist = max_distance, ignore_case = TRUE)
}, jarowinker = {
blocks <- stringdist_inner_join(data, data, by = column,
method = "jw", max_dist = max_distance, ignore_case = TRUE)
}, qgram = {
blocks <- stringdist_inner_join(data, data, by = column,
method = "qgram", max_dist = max_distance, ignore_case = TRUE)
}, {
stop("choose a valid method from levenshtein, cosine, jaccard, jaro-winker, qgram")
#从 levenshtein、cosine、jaccard、jaro-winker、qgram 中选择一个有效的方法
})
blocks <- subset(blocks, blocks$row.x < blocks$row.y) #过滤掉一些重复的拼接
blocks <- subset(blocks, select = -c(row.x, row.y)) #最后结果中不显示这个行号信息
return(blocks)
}
spatial_blocking 以空间邻近性作为分块标准分块
#' @title Spatial blocking
#' @description Creates blocks of entities that near spatially. Returns the pairs 创建在空间上临近的实体的块 返回一对对具有空间临近性的对pairs
#'
#' @param data A dataframe of entities
#' @param longitude The column name that contains the longitudes
#' @param latitude The column name that contains the latitudes
#' @param max_distance The maximal distance in meters allowed in a block 块内所允许的最大距离,以米为单位
#'
#' @return blocks A dataframe of pairs
#'
#' @export
function (data, longitude, latitude, max_distance)
{ #数据集 经度(列名)纬度(列名) 最大距离
blocks <- NULL
data$row <- rownames(data) #给data数据增加一列,为行的序号
if (is.null(longitude) | is.null(longitude)) {
stop("specify the columns of the longitude and the latitude")
#指定经度和纬度的列
}
if (is.na(match(longitude, names(data)))) {
stop("enter a valid column name for the longitude")
#输入的经度的列得在数据集中存在
}
if (is.na(match(latitude, names(data)))) {
stop("enter a valid column name for the latitude")
#输入的纬度的列得在数据集中存在
}
if (is.null(max_distance)) {
stop("set max_distance to the maximal distance in meters to create spatial\n blocks")
#将 max_distance 设置为以米为单位的最大距离以创建空间块
}
#geo_inner_join:Join two tables based on a geo distance of longitudes and latitudes根据经纬度的地理距离连接两个表
#这允许基于经度和纬度的组合进行连接.距离是根据 geosphere 包中的 distHaversine、distGeo、distCosine 等方法计算的。
# geo_inner_join(
# x,
# y,
# by = NULL, #Columns by which to join the two tables
# method = "haversine", #用于计算距离的方法:“haversine”(默认)、“geo”、“cosine”、“meeus”、“vincentysphere”、“vincentyellipsoid”之一
# max_dist = 1, #Maximum distance to use for joining
# distance_col = NULL, #如果给定,将添加一个具有此名称的列,其中包含传递给 distance 方法的两个额外参数之间的地理距离
# ...
#)
blocks <- geo_inner_join(x = data, y = data, by = c(longitude,
latitude), method = "haversine", max_dist = max_distance/1000,
unit = "km")
blocks <- subset(blocks, blocks$row.x < blocks$row.y) #过滤掉一些重复的拼接
blocks <- subset(blocks, select = -c(row.x, row.y)) #最后结果中不显示这个行号信息
return(blocks)
}
prefix_blocking 以具有相同前缀为标准分块
#' @title Prefix blocking
#' @description Creates blocks of entities that have the same prefix. Returns the pairs 创建具有相同前缀的实体的块 返回一对对具有相同前缀的实体的对pairs
#'
#' @param data A dataframe of entities
#' @param column The column name of the attribute on which the prefix should be calculated
#' @param prefix_size The maximal number of characters for prefix blocking
#'
#' @return blocks A dataframe of pairs
#'
#' @export
function (data, column, prefix_size)
{ #数据集 列名 前缀大小
if (is.null(column)) {
stop("select the column for prefix blocking") #选择前缀分块的列
}
if (is.na(match(column, names(data)))) {
stop("enter a valid column name") #选择的列得在数据集中存在
}
if (is.null(prefix_size)) {
stop("choose the prefix size (number of characters)")
#选择前缀大小(字符数)
}
blocks <- NULL
data$row <- rownames(data) #给data数据增加一列,为行的序号
data$prefix <- substring(data[[column]], 1, prefix_size)
#提取字符向量中的子字符串 把数据集中给定的column列的前缀提取出来放到新的一列
#通过常见的列或行名称合并两个数据框
#通过前缀这一列合并两个数据集
blocks <- merge(x = data, y = data, by = "prefix")
blocks <- subset(blocks, blocks$row.x < blocks$row.y) #过滤掉一些重复的拼接
blocks <- subset(blocks, select = -c(row.x, row.y)) #最后结果中不显示这个行号信息
blocks <- subset(blocks, select = -c(prefix)) #最后结果中不显示这个前缀信息
return(blocks)
}
suffix_blocking 以具有相同后缀为标准分块
#' @title Suffix blocking
#' @description Creates blocks of entities that have the same suffix. Returns the pairs
#'
#' @param data A dataframe of entities
#' @param column The column name of the attribute on which the suffix should be calculated
#' @param suffix_size The maximal number of characters for suffix blocking
#'
#' @return blocks A dataframe of pairs
#'
#' @export
function (data, column, suffix_size)
{
if (is.null(column)) {
stop("select the column for suffix blocking") #选择后缀分块的列
}
if (is.na(match(column, names(data)))) {
stop("enter a valid column name") #选择的列得在数据集中存在
}
if (is.null(suffix_size)) {
stop("choose the suffix size (number of characters)")
#选择后缀大小(字符数)
}
blocks <- NULL
data$row <- rownames(data) #给data数据增加一列,为行的序号
data$suffix <- str_sub(data[[column]], -suffix_size, -1)
#取出给定column列的后缀,并单独作为一列数据
#通过后缀这一列合并两个数据集
blocks <- merge(x = data, y = data, by = "suffix")
blocks <- subset(blocks, blocks$row.x < blocks$row.y) #过滤掉一些重复的拼接
blocks <- subset(blocks, select = -c(row.x, row.y)) #最后结果中不显示这个行号信息
blocks <- subset(blocks, select = -c(suffix)) #最后结果中不显示这个后缀信息
return(blocks)
}
Pairwise comparison 将分块后一块内的pairs进行相似度比较
text_similarity 文本相似度
我们在比较空间实体的名称时使用 Levenshtein
#' @title Pairwise textual similarity
#' @description Compares the pairs pairwise regarding a textual attribute. Returns a vector of text similarity 根据一个文本属性,成对比较一个个pairs对
#' 返回一个文本相似性的向量
#' @param data A dataframe of pairs
#' @param method A method for the text similarity, choose among levenshtein, cosine, jaccard, jaro-winker
#' @param column1 The first column name of the attribute that will be compared
#' @param column2 The second column name of the attribute that will be compared
#'
#' @return sim A vector of text similarities
#'
#' @export
function (data, method, column1, column2)
{
if (is.null(column1) | is.null(column2)) {
stop("select the columns to compare") #选择要比较的列
}
if (is.na(match(column1, names(data)))) {
stop("enter a valid column name for column1") #该列要实际存在
}
if (is.na(match(column2, names(data)))) {
stop("enter a valid column name for column2") #该列要实际存在
}
#stringdist:计算字符串之间的距离度量
# stringdist(
# a,
# b,
# method = c("osa", "lv", "dl", "hamming", "lcs", "qgram", "cosine", #"jaccard", "jw",
# "soundex"),
# useBytes = FALSE,
# weight = c(d = 1, i = 1, s = 1, t = 1),
# q = 1,
# p = 0,
# bt = 0,
# nthread = getOption("sd_num_thread")
#)
switch(method, levenshtein = {
return(1 - (stringdist(data[[column1]], data[[column2]],
method = "lv")/mapply(max, nchar(data[[column1]]),
nchar(data[[column2]]))))
}, cosine = {
return(1 - stringdist(data[[column1]], data[[column2]],
method = "cosine"))
}, jaccard = {
return(1 - stringdist(data[[column1]], data[[column2]],
method = "jaccard"))
}, jarowinker = {
return(1 - stringdist(data[[column1]], data[[column2]],
method = "jw"))
}, {
stop("choose a valid method from levenshtein, cosine, jaccard, jaro-winker")
})
}
spatial_similarity 空间相似度
#' @title Pairwise spatial similarity
#' @description Compares the pairs pairwise regarding a spatial attribute. Returns a vector of spatial similarity
#'
#' @param data A dataframe of pairs
#' @param lat1 The column name of the latitude of the first entity
#' @param long1 The column name of the longitude of the first entity
#' @param lat2 The column name of the latitude of the second entity
#' @param long2 The column name of the longitude of the second entity
#' @param max_distance The maximal distance allowed
#'
#' @return sim A vector of spatial similarities
#'
#' @export
function (data, lat1, long1, lat2, long2, max_distance)
{
if (is.null(lat1) | is.null(lat2) | is.null(long1) | is.null(long2)) {
stop("select the columns to compare") #选择要比较的列
}
if (is.na(match(lat1, names(data)))) {
stop("enter a valid column name for lat1")
}
if (is.na(match(long1, names(data)))) {
stop("enter a valid column name for long1")
}
if (is.na(match(lat2, names(data)))) {
stop("enter a valid column name for lat2")
}
if (is.na(match(long2, names(data)))) {
stop("enter a valid column name for long2")
}
distance <- distVincentyEllipsoid(data[, c(long1, lat1)],
data[, c(long2, lat2)])
distance <- 1 - (distance/max_distance)
distance <- ifelse(distance < 0, 0, distance)
}
semantic_similarity 语义相似度
计算语义相似度,理论方法参见上文成对比较中对计算语义相似度的介绍。
#' @title Pairwise semantic similarity
#' @description Compares the pairs pairwise regarding their semantic attributes. Returns a vector of semantic similarity
#'
#' @param data A dataframe of pairs
#' @param column1 The column name containing the semantics for the first entity
#' @param column2 The column name containing the semantics for the second entity
#' @param pythonpath The path where the python file is saved
#' @param method The method for the semantic similarity; choose between path (Path similarity), and wup (Wu&Palmer)
#'
#' @return sim A vector of semantic similarities
#'
#' @export
function (data, column1, column2, pythonpath, method)
{
if (is.null(column1) | is.null(column2)) {
stop("select the columns to compare")
}
if (is.na(match(column1, names(data)))) {
stop("enter a valid column name for column1")
}
if (is.na(match(column2, names(data)))) {
stop("enter a valid column name for column2")
}
use_python(pythonpath, required = T)
nltk <- import("nltk")
switch(method, wup = {
wup_python <- function(x, y) {
source_python("pythonscript/wup.py")
return(add(x, y))
}
}, path = {
wup_python <- function(x, y) {
source_python("pythonscript/path.py")
return(add(x, y))
}
}, {
stop("choose a valid method from wup and path")
# 从 wup 和 path 中选择一个有效的方法
})
wup_python_list <- function(text1, text2) {
if (is.na(text1) || text1 == "") {
return(0)
}
if (is.na(text2) || text2 == "") {
return(0)
}
text1 <- gsub("[[:punct:] ]+", " ", text1) #把text1中的“[[:punct:] ]+”用“ ”替换
text2 <- gsub("[[:punct:] ]+", " ", text2) #把text2中的“[[:punct:] ]+”用“ ”替换
if (strcmpi(text1, text2)) { #不区分大小写的比较
return(1)
}
p1 <- as.list(strsplit(text1, "\\s+")[[1]])
p2 <- as.list(strsplit(text2, "\\s+")[[1]])
if (length(intersect(p1, p2)) != 0) {
return(1)
}
else {
S <- c(0)
for (i in p1) {
for (j in p2) {
S <- c(S, wup_python(i, j)) #调用前面的switch里定义的函数
}
return(max(S))
}
}
}
return(mapply(wup_python_list, stringi::stri_enc_toutf8(data[[column1]]),
stringi::stri_enc_toutf8(data[[column2]])))
# 将带有已声明标记编码的字符串转换为 UTF-8 字符串
#以wup_python_list方法,后面两个参数是其输入
}
Labeling 标记
skyexf
#' @title SkyEx-F labeling
#' @description Pair Labeling using SkyEx-F
#'
#' @param data A dataframe of pairs
#' @param p A preference function (e.g. p<-high("sim1")*high("sim2"))
# 两列的组合,都是以多、哪个大为参考,这里是指的是pairs的效用在实际会选择,所有被考虑的属性的效用之和,但不会说一定是所有的属性的效用之和
#' @param label Name of the label column (e.g. "Class")
#' @param posclass How is the positive class expressed (e.g. 1)
#' @param negclass How is the negative class expressed (e.g. 0)
#'
#' @return of A skyexf object
#'
#' @export
function (data, p, label, posclass, negclass)
{ # 列
if (is.null(p)) {
stop("the preference is NULL")
}
if (is.null(label)) {
stop("select the column that contains the label") #选择包含标签的列
}
if (is.na(match(label, names(data)))) {
stop("enter a valid column name for the variable label")
}
if (!is.element(posclass, data[[label]])) {
stop(paste0("There is no ", posclass, " in ", label))
}
if (!is.element(negclass, data[[label]])) {
stop(paste0("There is no ", negclass, " in ", label))
}
data$rrow <- seq.int(nrow(data)) #新增一列,依次从1到这个数据集的行数
res <- psel(data, p, top = nrow(data))
#评估给定数据集的偏好,即返回给定偏好顺序的数据集的最大元素。
#第一个参数:数据集
#第二个参数:偏好
#分层的最大值:最大层数不超过原数据集的行数
#这里其实是将原数据集通过偏好进行k-best分层
#每层有多少个元素是不确定的,但是在同一层的元素在偏好上一定是等价的,层层递减的趋势
df <- data.frame(levels = numeric(), positives = numeric(),
precision = numeric(), recall = numeric(), stringsAsFactors = FALSE)
#定义一个数据框
k = 1
while (k <= max(res$.level)) {
tempres <- subset(res, res$.level <= k) #把res数据集中level字段≤k的行筛选出来
df <- rbind(df, data.frame(levels = k, positives = as.numeric(nrow(tempres)),
precision = as.numeric(nrow(subset(tempres, tempres[[label]] ==
posclass)))/as.numeric(nrow(tempres)), recall = as.numeric(nrow(subset(tempres,
tempres[[label]] == posclass)))/as.numeric(nrow(subset(res, res[[label]] == posclass)))))
#rbind 给数据框增加一行数据
k = k + 1 #天际线的k增加
}
#计算f-measure
df$fmeasure <- (2 * df$precision * df$recall/(df$precision + df$recall))
cut <- df[which.max(df$fmeasure), 1] #找出f-measure最大的
res$pred_class <- ifelse(res$.level <= cut, yes = posclass,
no = negclass)
res <- res[order(match(res$rrow, data$rrow)), ]
of <- list(classes = res$pred_class, analysis = df, k = df[which.max(df$fmeasure),
1], fmeasure = max(df$fmeasure))
class(of) <- "skyexf"
return(of)
}
-
因为精度为 p = T P T P + F P p = \frac{TP}{TP+FP} p=TP+FPTP,即引用相同物理实体并正确标记为positives的pairs数量除去所有被标记为positives的pairs数量,代码中precision = a s . n u m e r i c ( n r o w ( s u b s e t ( t e m p r e s , t e m p r e s [ [ l a b e l ] ] = = p o s c l a s s ) ) ) a s . n u m e r i c ( n r o w ( t e m p r e s ) ) \frac{as.numeric(nrow(subset(tempres, tempres[[label]] == posclass)))}{as.numeric(nrow(tempres))} as.numeric(nrow(tempres))as.numeric(nrow(subset(tempres,tempres[[label]]==posclass))),表示的意思是精度为当前天际线中被标记为positive class的数除以当前天际线中的所有pairs数。
-
因为召回率为 r = T P T P + F N r =\frac{TP}{TP+FN} r=TP+FNTP,表示的意思是引用相同物理实体并正确标记为positives的pairs数量除去所有引用自相同物理实体的pairs数量,代码中recall = a s . n u m e r i c ( n r o w ( s u b s e t ( t e m p r e s , t e m p r e s [ [ l a b e l ] ] = = p o s c l a s s ) ) ) a s . n u m e r i c ( n r o w ( s u b s e t ( r e s , r e s [ [ l a b e l ] ] = = p o s c l a s s ) ) ) \frac{as.numeric(nrow(subset(tempres, tempres[[label]] == posclass)))}{as.numeric(nrow(subset(res, res[[label]] == posclass)))} as.numeric(nrow(subset(res,res[[label]]==posclass)))as.numeric(nrow(subset(tempres,tempres[[label]]==posclass))),表示的意思是精度为当前天际线中被标记为positive class的数除以数据集中所有引自相同物理实体pairs数。
-
F-measure ( F 1 F_{1} F1) = 2 p × r p + r 2\frac{p \times r}{p+r} 2p+rp×r
代码中计算F-measure=df$fmeasure <- (2 * df$precision * df$recall/(df$precision + df$recall))
skyexd
#' @title SkyEx-D labeling
#' @description Pair Labeling using SkyEx-D
#' @param data A dataframe of pairs
#' @param p A preference function (e.g. p<-high("sim1")*high("sim2"))
#' @param simlist Similarities to be taken into consideration for the density function (e.g. simlist= c("sim1", "sim2"))
#' @param smooth.coefficient A smoothing coefficient
#' @param posclass How is the positive class expressed (e.g. 1)
#' @param negclass How is the negative class expressed (e.g. 0)
#'
#' @return od A skyexd object
#'
#' @export
#'
function (data, p, simlist, smooth.coefficient, posclass, negclass)
{
if (is.null(p)) {
stop("the preference is NULL")
}
data$rrow <- seq.int(nrow(data)) #新增一列,依次从1到这个数据集的行数
options(rPref.parallel = TRUE) #配置参数
res <- psel(data, p, top = nrow(data))
df <- data.frame(levels = numeric(), positives = numeric(),
meandist = numeric(), stringsAsFactors = FALSE)
k = 1
while (k <= max(res$.level)) {
dist <- rdist(subset(res[simlist], res$.level == k),
subset(res[simlist], res$.level > k))
tempres <- subset(res, res$.level <= k)
df <- rbind(df, data.frame(levels = k, positives = as.numeric(nrow(tempres)),
meandist = mean(dist)))
k = k + 1
}
df$sumdist <- df$meandist * df$positives
df$cumsumdist <- as.numeric(cumsum(as.numeric(df[order(df$levels), "sumdist"]))) #按照数据框的levels列进行排序
# cumsumdist是sumdist的累计和
df$CumDist <- df$cumsumdist/df$positives
n <- length(df$levels)
fdx <- vector(length = n)
for (i in 2:n) {
fdx[i - 1] <- (df$CumDist[i - 1] - df$CumDist[i])/(df$levels[i -
1] - df$levels[i])
}
fdx[n] <- (df$CumDist[n] - df$CumDist[n - 1])/(df$levels[n] -
df$levels[n - 1])
df$deriv <- fdx
smoothderiv <- smth(x = as.numeric(df$deriv), window = smooth.coefficient,
method = "gaussian")
kd <- which(smoothderiv < 0)[1]
res$pred_class <- ifelse(res$.level <= kd, yes = posclass,
no = negclass)
res <- res[order(match(res$rrow, data$rrow)), ]
df$smooth.deriv <- smoothderiv
od <- list(classes = res$pred_class, analysis = df[c("levels",
"positives", "deriv", "smooth.deriv")], k = kd)
class(od) <- "skyexd"
return(od)
}
基于开源项目的自有数据集(restaurant)跑通源码
源码参考:skyex-package
QuadFlex
两篇论文中都采用了四叉树的方法,但是github上源码却是从文本相似度、空间邻近性、文本前缀、文本后缀这四个方面分别考虑分块,考虑到原始数据集restaurants的数据结构特征:
(观察restaurant数据集的特点,其具有864个逻辑空间实体,两两成对,864*864≈777452,与前文描述的数据集大小一致——“对 777,452 对半手动标记数据集产生 0.87 的精度和 0.6 的召回率”)
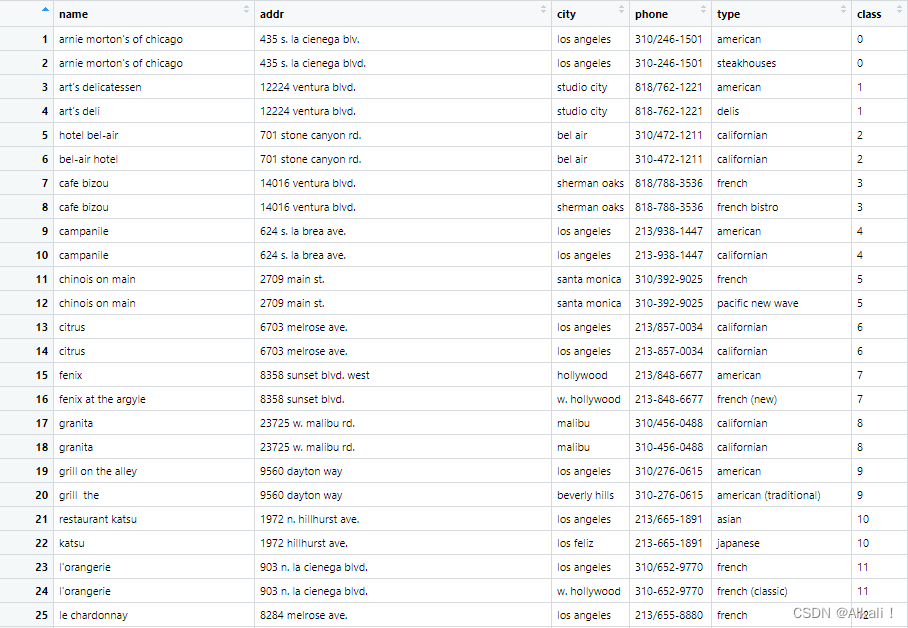
并未提供空间实体的经纬度信息,所以无法从空间邻近性的角度去进行分块,且论文中未提及从前缀以及后缀的角度去分块,故而采用从文本相似度的角度去分块。
而适用于文本相似性的属性为名称、用户名等属性,故而采用对空间实体的名称name的文本相似性进行分块,得到数据框blocks。
blocks <- textual.blocking(restaurants,"name","levenshtein",0.6)
#根据name列的模糊字符串匹配,对data进行自连接,模糊字符串匹配的方法是levenshtein方法,最大距离初步设置为0.6。
得到的数据框blocks的数据标题格式如下:
| name.x | addr.x | city.x | phone.x | type.x | class.x | name.y | addr.y | city.y | phone.y | type.y | class.y |
|---|
PAIRWISE COMPARISONS
论文中提及从文本相似性、语义相似度这两个角度考虑成对比较,源码中所涉及的从空间邻近度进行成对比较在原数据集上不可行,因为原数据集未涉及空间实体的经纬度信息。
text_similarity
考虑文本相似性时,字符串相似度指标通常适用于名称、用户名等属性。其他一些文本属性需要其他需要定制的指标。这里又因为我们当初分块是以空间实体的名称name来分块的,采用的也是文本相似度的分块方法,所以在对分块后形成的pairs再进行成对比较时,最好选择另外一个也可以使用文本相似度来衡量相似度的属性,在这里我们选择city属性来作为成对比较文本相似度的指标:
blocks$TextSim <- text.similarity(blocks,"levenshtein","city.x","city.y")
#使用levenshtein方法,对数据框blocks中的两列属性city.x和city.y进行文本相似性度量,文本相似性保存在新的一列TextSim中。
此时,数据框blocks的数据标题格式如下:
| name.x | addr.x | city.x | phone.x | type.x | class.x | name.y | addr.y | city.y | phone.y | type.y | class.y | TextSim |
|---|
semantic_similarity
语义相似度度量是针对类别、关键字或元数据等字段的相似性。
blocks$SemSim <- semantic.similarity(blocks,"type.x","type.y","C:\\Users\\86150\\anaconda3\\python.exe","wup")
#这里卡了一会儿,注意选择python路径时,可能有多个选择,要选择一个相关库多一点的。
#使用wup方法,度量pairs对类别type属性之间的语义相似度,结果存在数据框的新一列SemSim
此时,数据框blocks的数据标题格式如下:
| name.x | addr.x | city.x | phone.x | type.x | class.x | name.y | addr.y | city.y | phone.y | type.y | class.y | TextSim | SemSim |
|---|
Labeling
skyexf
在跑skyexf算法之前,我们可以发现,原先的初始数据集restaurants的有一列class我们还没有利用上,这里class的作用是:利用class的数字相同表示两个空间实体同属于一个物理实体。
所以我们可以先利用这个特点,作用到我们成对比较的pairs上,可以给blocks生成一个新的字段class,该字段表明这个pairs里的两个空间实体是否来自于同一个物理实体。
blocks$class <- as.numeric(blocks$class.x == blocks$class.y)
#如果blocks$class.x == blocks$class.y,则class=1,否则为0
这时我们再来理解skyexf算法的参数内涵:
function (data, p, label, posclass, negclass)
#' @param data A dataframe of pairs
#' @param p A preference function (e.g. p<-high("sim1")*high("sim2"))
# 两列的组合,都是以多、哪个大为参考,这里是指的是pairs的效用在实际会选择,所有被考虑的属性的效用之和,但不会说一定是所有的属性的效用之和
#' @param label Name of the label column (e.g. "Class")
#' @param posclass How is the positive class expressed (e.g. 1)
#' @param negclass How is the negative class expressed (e.g. 0)
data:经过成对比较后的pairs数据集,data里的每一行都是一个pairs对,有该pairs对的文本相似性TextSim与语义相似性SemSim信息。p:我们在进行对成对比较后的pairs对依据其效用进行rank时,需要一个排名的依据/偏好指标,这里是相似度越高,排名越高,则这里的p表示为:p <-high("TextSim")*high("SemSim")posclass, negclass:最终的判别结果要以什么形式呈现
此时,尽管还没有完全理解,我们已经可以试着跑一遍skyexf算法了:
p <-high("TextSim")*high("SemSim")
of <- skyexf(blocks,p,"class",1,0)
在Rstdio里面,经过skyexf跑出来的结果是这样:
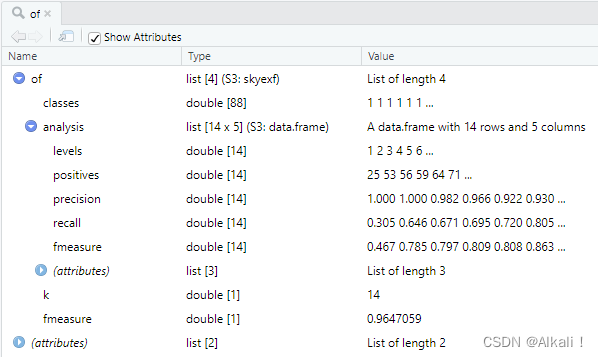
看了不是太明白是什么意思,于是可以将skyexf函数的语句,一步步执行来理解下,解析下其源码:
保证其传进来的参数是有效的
if (is.null(p)) {
stop("the preference is NULL")
}
if (is.null(label)) {
stop("select the column that contains the label")
}
if (is.na(match(label, names(data)))) {
stop("enter a valid column name for the variable label")
}
if (!is.element(posclass, data[[label]])) {
stop(paste0("There is no ", posclass, " in ", label))
}
if (!is.element(negclass, data[[label]])) {
stop(paste0("There is no ", negclass, " in ", label))
}
data$rrow <- seq.int(nrow(data))
效果是新增一列rrow,每一行中rrow的数据表示该行在数据集中的行号。
res <- psel(data, p, top = nrow(data)) 这一步实际上是在进行SkyRank
在data的基础上产生一个新的数据框res,他具有data数据框的基本列,以及新的一列.level。
该psel函数的作用是将数据框data的每一行数据按照偏好p进行分层,每层有多少个元素(包括多少行)是不确定的,但是在同一层的元素(一行)在偏好上一定是等价的,呈现层层递减的趋势,参数top = nrow(data)指定了若可以分的层数最多的情况下,不能超过原数据框的行数,也即每层至少得有一个元素,也即一行。
df <- data.frame(levels = numeric(), positives = numeric(), precision = numeric(), recall = numeric(), stringsAsFactors = FALSE)
定义一个数据框,指定每列的列名和属性:
| levels | positives | precision | recall |
|---|---|---|---|
| 天际线划到哪一层 | 这一层以上的pairs对数 | 精度 | 召回率 |
| numeric | numeric | numeric | numeric |
计算每一个天际线划分下pairs的数量、精度、召回率
我们可以将这步操作封装成一个函数(防止出错,参数与skyexf基本一致),作用于res,返回df,然后再看看df长什么样。
#定义一个函数f
f <- function (data, p, label, posclass, negclass)
{
res <- psel(data, p, top = nrow(data))
df <- data.frame(levels = numeric(), positives = numeric(), precision = numeric(), recall = numeric(), stringsAsFactors = FALSE)
k = 1
while (k <= max(res$.level)) {
tempres <- subset(res, res$.level <= k)
df <- rbind(df, data.frame(levels = k, positives = as.numeric(nrow(tempres)),
precision = as.numeric(nrow(subset(tempres, tempres[[label]] == posclass)))/as.numeric(nrow(tempres)),
recall = as.numeric(nrow(subset(tempres, tempres[[label]] == posclass)))/as.numeric(nrow(subset(res, res[[label]] == posclass)))))
k = k + 1
}
return(df)
}
df <- f(blocks,p,"class",1,0)
#运行这个函数f,得到数据框df
此时我们可以看下df长什么样,从而分析理解其含义:
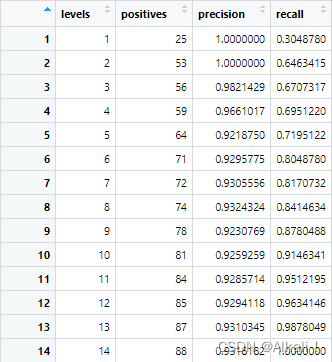
计算每个天际线下的f-measure:df$fmeasure <- (2 * df$precision * df$recall/(df$precision + df$recall))
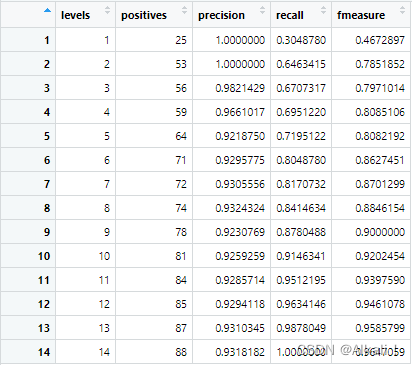
找到f-measure最大值时所对应的天际线划分:cut <- df[which.max(df$fmeasure), 1]
可以知道,天际线划到哪可以使f-measure最大

在数据集res上产生一列pred_class,如果包括在最终确定的天际线cut内,则标记为1,否则为0
res$pred_class <- ifelse(res$.level <= cut, yes = posclass, no = negclass)
将数据集res中的pairs按初始时在blocks里的行序号排序
res <- res[order(match(res$rrow, blocks$rrow)), ]
汇总成一个返回值:一个list对象
of <- list(classes = res$pred_class, analysis = df, k = df[which.max(df$fmeasure), 1], fmeasure = max(df$fmeasure))
class(of) <- "skyexf" #把list of的数据类型抽象出来,叫"skyexf" 可以理解成抽象出一个类来
return(of) #作为返回值返回
由此可知,一个skyexf object本质上是一个list,属性为:
classes:每个空间实体对pairs是否属于同一个物理实体,是则标记为1,否则标记为0,这个属性是对先前每对的标记结果汇总(数据上即为res$pred_class)。analysis:在每种天际线划分下的分析结果:包括当前天际线划分、当前天际线划分下能包括的实体对对数、精度、召回率、f-measure。

k:最终使得f-measure最大情况下的天际线划分fmeasure:对应的最大f-measure值
总结
再回过头来看我们之前没解析skyexf结果前就跑出来的结果:

和上述分析结果一致。
数据结果分析:
因为of对象中的classes为全1,blocks或res中的pairs以skyexf方法判别,两两都属于同一个空间实体。
我们回过头来观察原始数据集restaurants,它有864个空间实体对象,最终通过skyexf方法,能够判断其中的88对空间实体来源于同一个物理空间,其余都不是来自同一个物理空间实体。
skyexd
在跑通并理解skyexf算法后,我们可以试着用拆解skyexd函数代码一步步执行的方式来理解源码。
算法前处理
if (is.null(p)) { #确定偏好非空
stop("the preference is NULL")
}
data$rrow <- seq.int(nrow(data)) #新增一列,依次从1到这个数据集的行数
options(rPref.parallel = TRUE) #配置参数
res <- psel(data, p, top = nrow(data)) #天际线分层
df <- data.frame(levels = numeric(), positives = numeric(),
meandist = numeric(), stringsAsFactors = FALSE)
#定义一个数据框
定义一个数据框,指定每列的列名和属性:
| levels | positives | meandist |
|---|---|---|
| 天际线划到哪一层 | 这一层以上的pairs对数 | 类间距离 |
| numeric | numeric | numeric |
求出每个天际线划分下类间距离的平均值
k = 1
while (k <= max(res$.level)) {
dist <- rdist(subset(res[simlist], res$.level == k),
subset(res[simlist], res$.level > k))
tempres <- subset(res, res$.level <= k)
df <- rbind(df, data.frame(levels = k, positives = as.numeric(nrow(tempres)),
meandist = mean(dist)))
k = k + 1
}
直接看看不明白,可以先封装成一个函数来看,看看执行完的结果是什么。函数的参数最好和skyexd一致,不容易出错。
#定义一个函数f
f <- function (data, p, simlist)
{
if (is.null(p)) {
stop("the preference is NULL")
}
data$rrow <- seq.int(nrow(data)) #新增一列,依次从1到这个数据集的行数
options(rPref.parallel = TRUE) #配置参数
res <- psel(data, p, top = nrow(data))
df <- data.frame(levels = numeric(), positives = numeric(),
meandist = numeric(), stringsAsFactors = FALSE)
k = 1
while (k <= max(res$.level)) {
dist <- rdist(subset(res[simlist], res$.level == k),
subset(res[simlist], res$.level > k))
tempres <- subset(res, res$.level <= k)
df <- rbind(df, data.frame(levels = k, positives = as.numeric(nrow(tempres)), meandist = mean(dist)))
k = k + 1
}
return(df)
}
传入参数:
p <-high("TextSim")*high("SemSim")
simlist= c("TextSim", "SemSim")
执行命令:
df <- f(blocks,p,simlist)
该函数运行完,返回的df为:
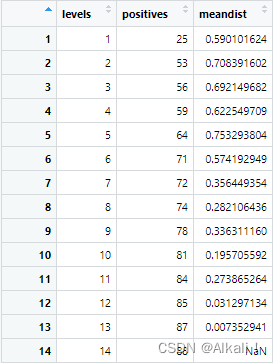
回顾前面的论文提到的类间距离的均值:
μ
d
=
∑
d
(
p
k
,
p
−
k
)
∣
P
k
∣
\mu_{d}=\frac{\sum d(p^{k},p^{-k})}{|P_{k}|}
μd=∣Pk∣∑d(pk,p−k)
where
∣
P
k
∣
|P_{k}|
∣Pk∣ is the number of pairs from the
1
s
t
1^{st}
1st to the
k
t
h
k^{th}
kth skyline ,
p
k
p^{k}
pk is a pair in
P
k
P^{k}
Pk ,
p
−
k
p^{-k}
p−k is a pair in
P
−
P
k
P-P^{k}
P−Pk , and
d
(
p
k
,
p
−
k
)
d(p^{k},p^{-k})
d(pk,p−k) is the distance between
p
k
p^{k}
pk and
p
−
k
p^{-k}
p−k.
结合代码,我们终于明白这几步是在干嘛。
k = 1
while (k <= max(res$.level)) {
dist <- rdist(subset(res[simlist], res$.level == k),
subset(res[simlist], res$.level > k)) #类间距离
# rdist 计算一个矩阵中观察值之间的成对距离并返回一个 dist 对象
# 计算所有配对之间的完整欧氏距离矩阵
tempres <- subset(res, res$.level <= k)
df <- rbind(df, data.frame(levels = k, positives = as.numeric(nrow(tempres)),
meandist = mean(dist))) #得出在k天际线划分下的类间距离的均值
k = k + 1
}
计算几类sum
-
df$sumdist <- df$meandist * df$positives
s u m d i s t = 类间平均距离 × 当前天际线划分下 p o s i t i v e sumdist=类间平均距离\times当前天际线划分下positive sumdist=类间平均距离×当前天际线划分下positive c l a s s 的个数 class的个数 class的个数 -
df$cumsumdist <- as.numeric(cumsum(as.numeric(df[order(df$levels), "sumdist"])))
因为本身df就已经按levels列排好序,所以这里order排序其实也可以不弄
c u m s u m d i s t 是 s u m d i s t 的累加和 cumsumdist是sumdist的累加和 cumsumdist是sumdist的累加和 -
df$CumDist <- df$cumsumdist/df$positives
计算 μ d ′ ( k ) μ' _{d}(k) μd′(k)
论文中提到:
为了找到“灰色区域”,我们注意一阶导数何时将其斜率变为负值。 为了计算 μ d ′ ( k ) μ' _{d}(k) μd′(k),我们估计每个点 k k k 中
μ d ′ ( k ) μ' _{d}(k) μd′(k)的值: μ d ′ ( k ) = ∂ ∂ k ≈ μ d ( k + 1 ) − μ d ( k ) 1 μ' _{d}(k)=\frac{\partial}{\partial k}≈\frac{μ_{d}(k+1)-μ_{d}(k)}{1} μd′(k)=∂k∂≈1μd(k+1)−μd(k)
我们将代码封装成一个函数:
#定义一个函数f
f <- function (df)
{
n <- length(df$levels)
fdx <- vector(length = n)
for (i in 2:n) {
fdx[i - 1] <- (df$CumDist[i - 1] - df$CumDist[i])/(df$levels[i -
1] - df$levels[i])
}
fdx[n] <- (df$CumDist[n] - df$CumDist[n - 1])/(df$levels[n] -
df$levels[n - 1])
df$deriv <- fdx
return(df)
}
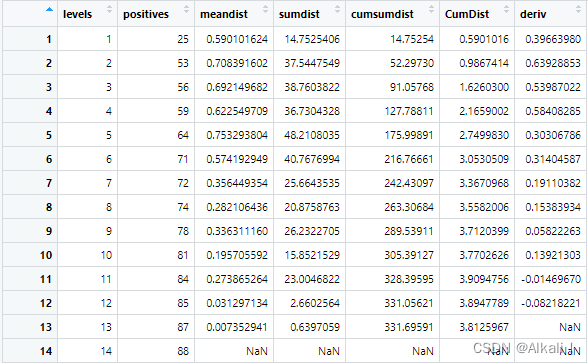
平滑数值数据
smoothderiv <- smth(x = as.numeric(df$deriv), window = smooth.coefficient, method = "gaussian")
# x 要平滑的值的数值向量
# window 平滑系数
method : 使用高斯函数
1
σ
2
π
e
−
(
x
−
μ
)
2
/
2
σ
2
\frac{1}{\sigma \sqrt{2\pi}}e^{-(x-\mu)^{2}/2\sigma^{2}}
σ2π1e−(x−μ)2/2σ2平滑
μ
d
′
(
k
)
μ' _{d}(k)
μd′(k)
这里的平滑系数我们代入0.1试试
smoothderiv <- smth(x = as.numeric(df$deriv), window = 0.1, method = "gaussian")
根据一阶导数 μ d ′ ( k ) μ' _{d}(k) μd′(k)何时第一次为负值求出 k d k_{d} kd
kd <- which(smoothderiv < 0)[1]

这里我们可以知道
k
d
=
11
k_{d}=11
kd=11
根据 k d k_{d} kd这一天际线进行正负类划分
res <- psel(blocks, p, top = nrow(blocks))
res$pred_class <- ifelse(res$.level <= kd, yes = 1, no = 0)
将数据集res中的pairs按初始时在blocks里的行序号排序
res <- res[order(match(res$rrow, blocks$rrow)), ]
df$smooth.deriv <- smoothderiv
汇总成一个返回值:一个list对象
od <- list(classes = res$pred_class, analysis = df[c("levels", "positives", "deriv", "smooth.deriv")], k = kd)
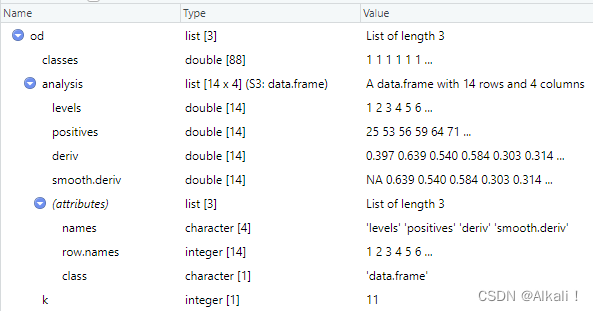
由此可知,一个skyexd object本质上是一个list,属性为:
-
classes:每个空间实体对pairs是否属于同一个物理实体,是则标记为1,否则标记为0,这个属性是对先前每对的标记结果汇总(数据上即为res$pred_class)。 -
analysis:在每种天际线划分下的分析结果 : 类间平均距离、类间平均距离的一阶导数、高斯函数平滑过后的类间平均距离的一阶导数。
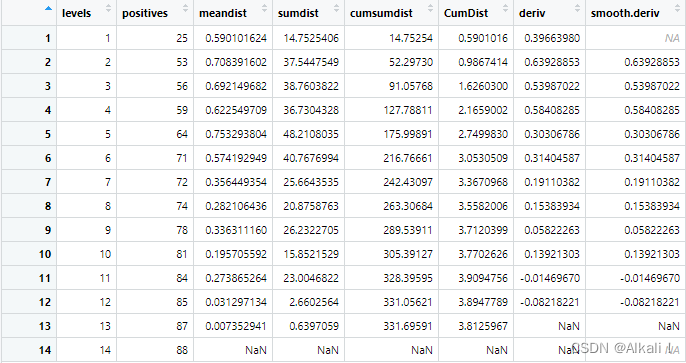
-
kd:由此方法得到kd
总结
数据结果分析:
观察od对象的classes值:

其中class为0表示该pairs不属于同一个物理空间实体,为1的表示该pairs属于同一个物理空间实体。
我们回过头来观察原始数据集restaurants,它有864个空间实体对象,最终通过skyexd方法,能够判断其中的84对空间实体来源于同一个物理空间,其余都不是来自同一个物理空间实体。
基于开源项目的自有数据集(data)跑通源码
观察data数据集的特点,其直接描述的是pairs,而不是单独的逻辑空间实体,共有1500对pairs,与前文描述的数据集大小一致——“对 1,500 对手动标记的数据集产生 0.85 的精度和 0.85 的召回率”)
由于在针对restaurant数据集的学习中,我们具体了解了skyexf和skyexd算法的细节,下面我们直接跑算法即可。