顾得泉:个人主页
个人专栏:《Linux操作系统》 《C/C++》 《LeedCode刷题》
键盘敲烂,年薪百万!
一、盛水最多的容器
题目链接:盛最多水的容器
题目描述
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
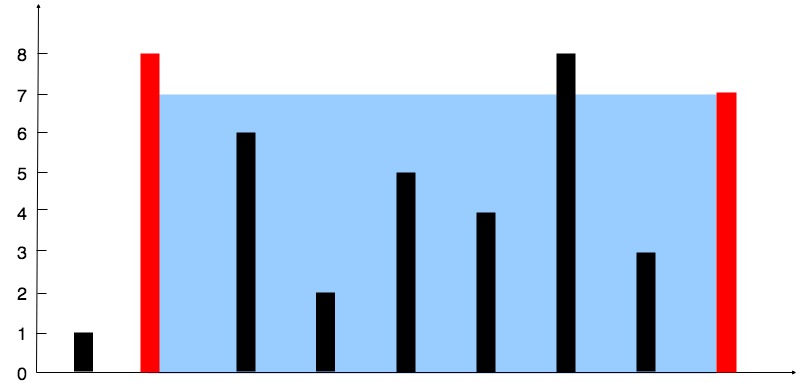
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
解法
设两个指针left,right分别指向容器的左右两个端点,此时容器的容积:
v = (right - left) * min( height[right], height[left])
容器的左边界为height[left] ,右边界为height[right]
为了方便叙述,我们假设「左边边界」小于「右边边界」
如果此时我们固定一个边界,改变另一个边界,水的容积会有如下变化形式:
容器的宽度一定变小。
由于左边界较小,决定了水的高度。如果改变左边界,新的水面高度不确定,但是一定不会超过右边的柱子高度,因此容器的容积可能会增大。
如果改变右边界,无论右边界移动到哪里,新的水面的高度一定不会超过左边界,也就是不会超过现在的水面高度,但是由于容器的宽度减小因此容器的容积一定会变小的。
由此可见,左边界和其余边界的组合情况都可以舍去。所以我们可以(left++跳过这个边界,继续去判断下一个左右边界。
当我们不断重复上述过程,每次都可以舍去大量不必要的枚举过程,直到left与right相遇。期间产生的所有的容积里面的最大值,就是最终答案。
代码实现
class Solution
{
public:
int maxArea(vector<int>& height)
{
int left = 0, right = height.size() - 1, ret = 0;
while(left<right)
{
int v = (min(height[left], height[right]) * (right - left));
ret = max(ret, v);
if(height[left] > height[right])
right--;
else
left++;
}
return ret;
}
};二、有效三角形的个数
题目链接:有效三角形的个数
题目描述
给定一个包含非负整数的数组 nums ,返回其中可以组成三角形三条边的三元组个数。
示例 1:
输入: nums = [2,2,3,4] 输出: 3 解释:有效的组合是: 2,3,4 (使用第一个 2) 2,3,4 (使用第二个 2) 2,2,3
示例 2:
输入: nums = [4,2,3,4] 输出: 4
提示:
1 <= nums.length <= 10000 <= nums[i] <= 1000
解法
解法一(暴力求解)(会超时)
算法思路:
三层for循环枚举出所有的三元组,并且判断是否能构成三角形。
虽然说是暴力求解,但是还是想优化一下:
判断三角形的优化:
如果能构成三角形,需要满足任意两边之和要大于第三边。但是实际上只需让较小的两条边
之和大于第三边即可。
因此我们可以先将原数组排序,然后从小到大枚举三元组,一方面省去枚举的数量,另一方
面方便判断是否能构成三角形。
解法二(排序+双指针):
算法思路:
先将数组排序。
根据「解法一」中的优化思想,我们可以固定一个「最长边」,然后在比这条边小的有序数组中找出一个二元组,使这个二元组之和大于这个最长边。由于数组是有序的,我们可以利用「对撞指针」来优化。
设最长边枚举到1位置,区间[left,right]是位置左边的区间(也就是比它小的区间)︰
如果nums [left] + nums[right] > nums[i]:
说明[left, right - 1]区间上的所有元素均可以与nums[right]构成比nums[i]大的二元组
满足条件的有right - left种
此时right位置的元素的所有情况相当于全部考虑完毕,right-- ,进入下一轮判断。
如果nums [left] + nums[right] <= nums[i] :
说明left位置的元素是不可能与[left + 1,right]位置上的元素构成满足条件的二元组
left位置的元素可以舍去,left++进入下轮循环
代码实现
class Solution
{
public:
int maxArea(vector<int>& height)
{
int left = 0, right = height.size() - 1, ret = 0;
while(left<right)
{
int v = (min(height[left], height[right]) * (right - left));
ret = max(ret, v);
if(height[left] > height[right])
right--;
else
left++;
}
return ret;
}
};三、查找总价为目标值的两个商品
题目链接:查找总价格为目标值的两个商品
题目描述
购物车内的商品价格按照升序记录于数组 price。请在购物车中找到两个商品的价格总和刚好是 target。若存在多种情况,返回任一结果即可。
示例 1:
输入:price = [3, 9, 12, 15], target = 18 输出:[3,15] 或者 [15,3]
示例 2:
输入:price = [8, 21, 27, 34, 52, 66], target = 61 输出:[27,34] 或者 [34,27]
提示:
1 <= price.length <= 10^51 <= price[i] <= 10^61 <= target <= 2*10^6
解法
a.初始化left ,right分别指向数组的左右两端(这里不是我们理解的指针,而是数组的下标)
b.当left < right的时候,一直循环
i. 当nums[left] + nums[right] == target时,说明找到结果,记录结果,并且返回;
ii.当nums[left] + nums[right] < target时:
对于nums[left]而言,此时nums[right]相当于是nums [left]能碰到的最大值(别忘了,这里是升序数组哈~)。如果此时不符合要求,说明在这个数组里面,没有别的数符合nums[left]的要求了(最大的数都满足不了你,你已经没救了)。因此,我们可以大胆舍去这个数,让 left++,去比较下一组数据;
那对于nums[right]而言,由于此时两数之和是小于目标值的,nums[right]还可以选择比nums[left]大的值继续努力达到国标值,因此right指针我们按兵不动;
iii.当nums[left] + nums[right1> target时,同理我们可以舍去nums[right](最小的数都满足不了你,你也没救了)。让right--,继续比较下一组数据,而left指针不变(因为他还是可以去匹配比nums[right]更小的数的)。
代码实现
class Solution
{
public:
vector<int> twoSum(vector<int>& price, int target)
{
int left = 0, right = price.size() - 1;
while(left < right)
{
int sum = price[left] + price[right];
if(sum < target)
left++;
else if(sum > target)
right--;
else
return {price[left], price[right]};
}
return {0,0};
}
};结语:今日的刷题分享到这里就结束了,希望本篇文章的分享会对大家的学习带来些许帮助,如果大家有什么问题,欢迎大家在评论区留言~~~