目录
二叉树
二叉树的分类(目前只谈两种)
满二叉树
完全二叉树
二叉树的性质(其余的可以自己总结)
选择练习
二叉树的存储结构
顺序存储方式
链式存储方式
二叉树
定义:二叉树是一种特殊的树状数据结构,它由多个节点组成,每个节点最多有两个子节点(左结点和右结点)这些子节点可以为空,任意的二叉树均由以下几种情况复合而成的:

因此我们可以得到以下结论:
- 二叉树的度小于等于2,二叉树的度不一定等于2,但是度为2的树就是二叉树
- 二叉树是有序树,子树有左右之分,不能颠倒
二叉树的分类(目前只谈两种)

满二叉树
定义:每一层的结点数都达到最大值的二叉树称为满二叉树
若二叉树层数为k,且结点总数为(2^k)-1 ,则为满二叉树
完全二叉树
定义:二叉树的最后一层是不满情况的二叉树称为完全二叉树,满二叉树是一种特殊的完全二叉树
若二叉树层数为k,且树中结点总数为[2^(k-1) ,(2^k) - 1],则为完全二叉树
二叉树的性质(其余的可以自己总结)
1. 若规定根节点的层数为1,则一棵非空二叉树的第k层上最多有2^(k-1)个结点
2. 若规定根节点的层数为1,则深度为k的二叉树的最大结点总数为(2^k) - 1
3. 若规定根节点的层数为1,则深度为k的二叉树的最小结点总数为2^(k - 1)
4. 完全二叉树中,度为2的结点总数 = 叶子结点总数 - 1
5. 任意一棵二叉树, 叶子节点总数 = 分支节点总数 + 1(根节点)
6. 任意一棵二叉树,结点总数 = 叶子结点总数 + 分支节点总数(度为2的结点)
7. 对于一颗完全二叉树,2 * 叶子结点总数 + 度为1的结点总数 - 1 = 结点总数
8. 完全二叉树 总结点数为偶数 则度为1的结点数为1 总节点数为奇数 则度为1的结点数为0
9. 若规定根节点的层数为1,则具有n个结点的二叉树的深度,h = (log以2为底n+1的对数)
10. 对于具有n个结点的完全二叉树,如果按照从上至下从左至右的数组顺序对所有节点从0开始编号,则对于序号为i的结点有:
- 若i=0,i为根节点下标,无双亲节点
- 若i>0,i下标的结点的双亲结点的下标为(i-1)/ 2
- 若i>0,i下标的结点的左孩子结点的下标为2 * i +1
- 若i>0,i下标的结点的左孩子结点的下标为2 * i +2
-
对于节点 i,若 2 * i + 1 < n,则节点 i 有左孩子。若 2 * i + 1 >= n,则节点 i 没有左孩子
-
对于节点 i,若 2 * i + 2 < n,则节点 i 有右孩子。若 2 * i + 2 >= n,则节点 i 没有左孩子

选择练习
1、某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为(B)
A 不存在这样的二叉树
B 200
C 198
D 199
结点总数 = 叶子结点总数 + 分支结点总数(度为2的结点) 399 = ? + 199 ? = 2002、在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )
A n
B n+1
C n-1
D n/2
//文字描述 完全二叉树中,度为2的结点总数 = 叶子结点总数 - 1 又因为,叶子结点总数 + 度为1的结点总数 + 度为2的结点总数= 2n 则可得:2*叶子结点总数 + 度为1的结点总数 - 1 = 2n 完全二叉树中,度为1的结点总数只能为0或1,由于2n为偶数,故度为1的结点总数 = 1 因此,叶子结点总数 = n //简化描述 完全二叉树中,有n2 = n0 - 1 再根据题设条件,得n0 + n1 + n2 = 2n 则可得:2n0 + n1 - 1 = 2n 完全二叉树中,n1只能为0或1,由于2n为偶数,故n1 = 1 因此,n0 = n3、一棵完全二叉树的节点数位为531个,那么这棵树的高度为(B )
A 11
B 10
C 8
D 12
若二叉树层数为k,且树中结点总数为[2^(k-1) ,(2^k) - 1],则为完全二叉树 A:[2^(11-1) ,(2^11) - 1] = [1024,2047] 1024 > 531 B:[2^(10-1) ,(2^10) - 1] = [512,1023] 512 < 531 < 1023 C:[2^(8-1) ,(2^8) - 1] = [128,511] 511 < 531 D:[2^(12-1) ,(2^12) - 1] = [2048,4095] 2048 > 5314、一个具有767个节点的完全二叉树,其叶子节点个数为(B)
A 383
B 384
C 385
D 386
完全二叉树 总结点数为偶数 则度为1的结点数为1 总节点数为奇数 则度为1的结点数为0 2 * 叶子结点总数 + 度为1的结点总数 - 1 = 结点总数 767为奇数,故度为1的结点总数为0,故: 2 * 叶子结点总数 - 1 = 结点总数 2 * ? - 1 = 767 ? = 384
二叉树的存储结构
顺序存储方式
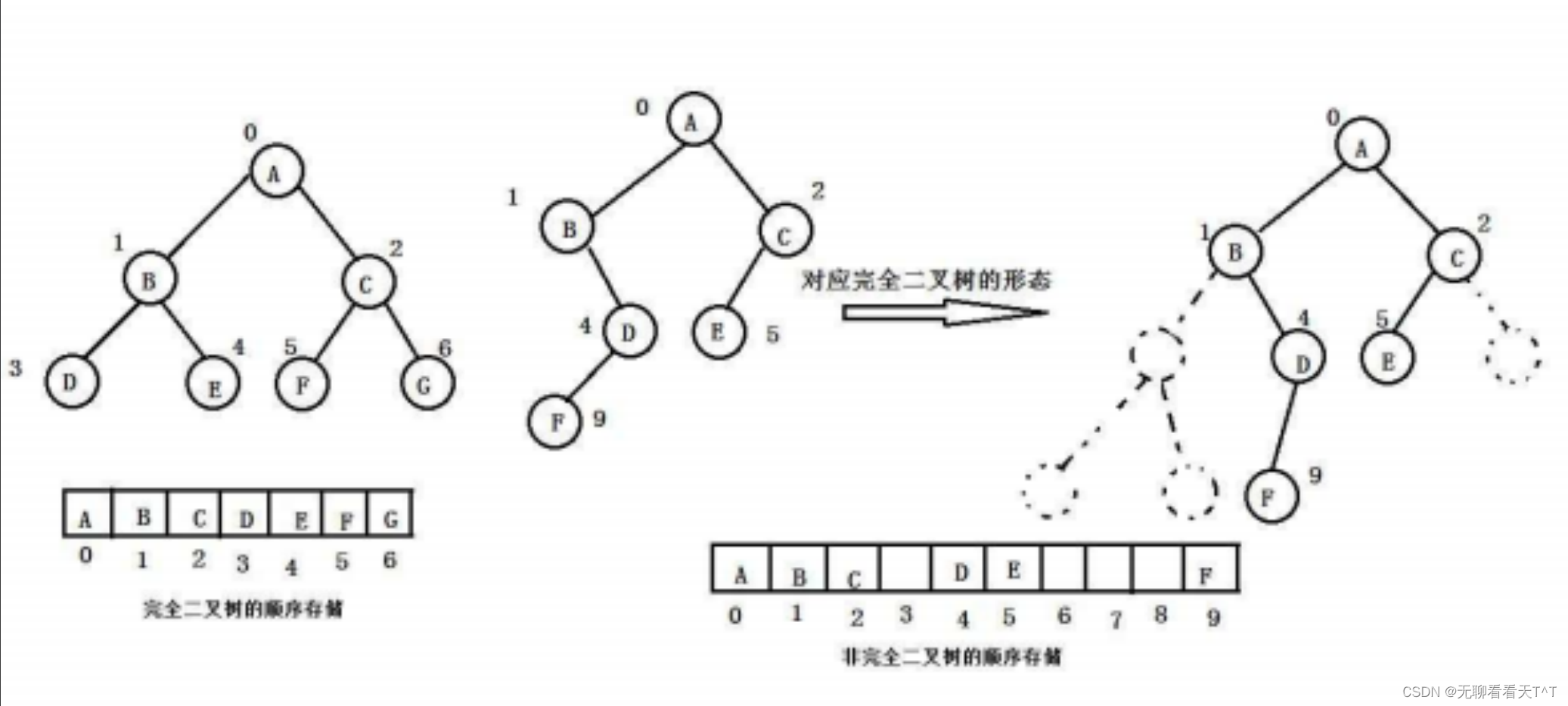
顺序存储方式即使用数组为底层逻辑进行存储,一般用于实现完全二叉树,因为对不完全二叉树使用顺序存储会存在空间浪费:
二叉树顺序存储在物理逻辑上是一个数组,在虚拟逻辑上是一颗二叉树
链式存储方式
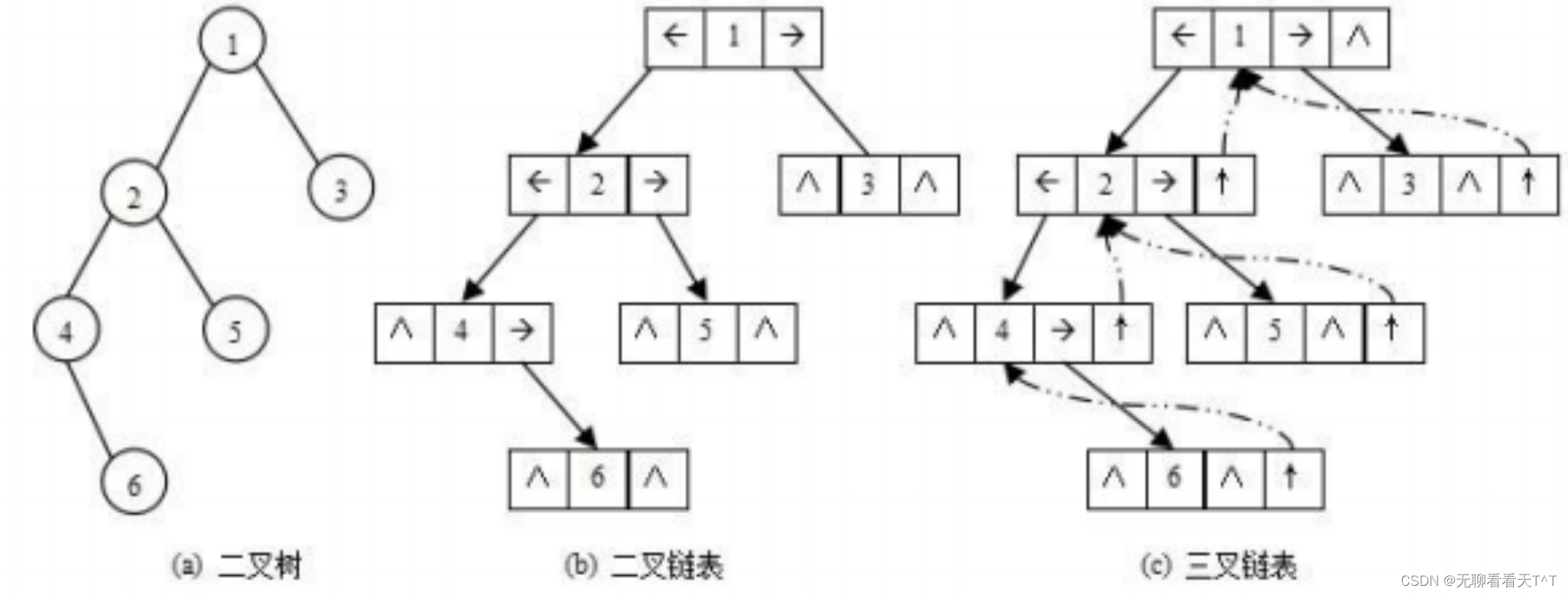
链式存储方式即使用链表为底层逻辑进行存储,同时链表还可以表示二叉树中各元素间的逻辑关系。通常的方法是链表中每个结点由三个域组成,数据域和左右指针域,左右指针分别用来给出该结点左孩子和右孩子所在的链结点的存储地址。链式结构又分为二叉链表和三叉链表,前我们学习的一般都是二叉链,在学习至红黑树时会用到三叉链......
~over~