n 座城市，从 0 到 n-1 编号，其间共有 n-1 条路线。因此，要想在两座不同城市之间旅行只有唯一一条路线可供选择（路线网形成一颗树）。去年，交通运输部决定重新规划路线，以改变交通拥堵的状况。

路线用 connections 表示，其中 connections[i] = [a, b] 表示从城市 a 到 b 的一条有向路线。

今年，城市 0 将会举办一场大型比赛，很多游客都想前往城市 0 。

请你帮助重新规划路线方向，使每个城市都可以访问城市 0 。返回需要变更方向的最小路线数。

题目数据 保证 每个城市在重新规划路线方向后都能到达城市 0 。

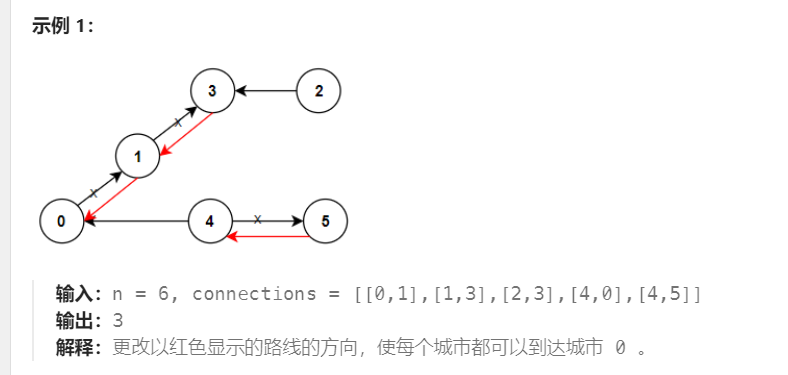
因为图是一个连通图，建图时把图看成一个无向图，实际存在的边权值为1，不存在的边权值为0，可以 从 顶点 0 遍历到所有顶点。遇到权值为0的边，

如果遇到反向的边，结果加1。

所以从0开始遍历，加上边的权值即可。

class Solution {
public:
    vector<vector<pair<int,int>>>g;
    int res=0;
    void dfs(int cur,int pre){
        for(auto ne:g[cur]){
            if(ne.first==cur||ne.first==pre)continue;
            res+=ne.second;
            dfs(ne.first,cur);
        }
    }
    int minReorder(int n, vector<vector<int>>& edge) {
        g.resize(n);
        for(int i=0;i<n-1;i++){
            g[edge[i][0]].push_back({edge[i][1],1});
            g[edge[i][1]].push_back({edge[i][0],0});
        }
        dfs(0,-1);
        return res;
    }
};