西工大计算机学院计算机系统基础实验一（函数编写15~17）

还是那句话，稳住心态，稳住心态，稳住心态。心里别慌，心里别慌，心里别慌。

第15题，howManyBits，返回用二进制补码形式表示x所需的最小二进制位数。比如howManyBits(12) = 5，12可以被表示为0 1100B，最高位的0为符号位，这样子一共需要5个二进制位来表示x；再比如howManyBits(298) = 10，298可以被表示为01 0010 1010B，最高位的0为符号位，这样子一共需要10个二进制位来表示x；接着比如howManyBits(-5) = 4，-5可以被表示为0xFFFF FFFB，从左到右删除掉连续的1，但最后仍还剩下一个1，即得到了1011B，最高位的1为符号位，这样子一共需要4个二进制位来表示x（1011B各位取反加一可以得到0101B也就是5）；接着howManyBits(0) = 1，0可以被表示为0B，符号位为0，一共需要1个二进制位；howManyBits(-1) = 1，-1可以被表示为1B，符号位为1，一共需要1个二进制位；在这里0被当作正的0而不是负的0，就好像int型的0是0x0而不是0x8000 0000一样。最后一个例子howManyBits(0x80000000) = 32，0x8000 0000，从左到右删除掉连续的1，但最后仍还剩下一个1，结果还是0x8000 0000，最高位为符号位，这样子一共需要32个二进制位来表示x。那么我们该怎么写出这个函数呢？

为了便于思考，我们首先先分两类讨论。第一类，当x为正数时，我们可以简单的将x*2，也就是将x左移一位，然后统计x<<1中有几位，比如x=5=101B，x<<1=1010B，这时x<<1中有4位，所以用二进制补码表示x需要4位，而事实也正好是这样；第二类，当x为负数时，就不能简单的统计x<<1中的位数了，比如-5=0xFFFF FFFB，(-5)<<1之后的结果还是0xFFFF FFF6，统计其中的位数，发现还是32位，所以不能简单的统计x<<1中的位数。那么我们该如何去掉从左到右删除掉连续的1，只留下一个1呢？发现可以通过异或的方法，x^(x<<1)，这样子就去掉了连续的1，只留下一个1啦！而对于正数来说，x^(x<<1)中的比特位数与x<<1一样。所以综上所述，无论x是正数还是负数，都可以只统计x^(x<<1)中的比特位数。在这里引入变量"int temp=x^(x<<1)"。

接着如何高效的统计temp中的比特位数呐？有这么一种思路，先看能不能用16位表示x，如果16位不够，那么记录下来16位不够，然后让temp=temp>>16，接着看8位够不够表示此时的temp，也就是8位够不够表示x^(x<<1)的高8位，如果能够的话，怀疑8位多了，所以记录下来8位足够，然后temp还是等于temp，接着看4位够不够表示此时的temp... ...下面结合例子来讲讲吧：

假设有一个变量x，其十六进制表示形式为0x0177 7FFF，那么temp为0x0399 8001。先看0x0399 8001可以被用16位非补码表示嘛？（因为temp=x^(x<<1)已经考虑了符号位的问题，所以这里问题只需要简简单单的考虑即可）发现不够，所以记录下来先需要16位，这样子低位的16位已经被记录下来了，把高16位拿到低16位看低16位的情况，也就是看0x0000 0399。0x0000 0399能被8位表示嘛？发现不够，所以记录下来还需要8位，这样子第16到第23位已经被记录下来了，再把8位拿到低位，即得到了0x0000 0003。0x0000 0003能被4位表示嘛？发现绰绰有余，所以记录下来不需要4位，然后不把4位拿到低位，还是0x0000 0003，它能被2位表示嘛？发现刚刚好，但是仍然记录下来不需要2位，然后不把2位拿到低位，还是0x0000 0003，他能被1位表示嘛？发现不够，所以记录下来需要1位。这时还少计算了1位，所以还要加1。

现在结合案例，我们思考该如何编写代码呢？首先如何判断能不能被16、8、4、2、1位表示呢？右移16、8、4、2、1位之后两次逻辑取非即可。那么如何记录下来需要16、8、4、2、1位呢？右移16、8、4、2、1位之后两次逻辑取非的结果，再左移4、3、2、1、0位即可。那么如何判断是否需要把temp的高位移到低位呢？让temp右移“右移16、8、4、2、1位之后两次逻辑取非的结果”即可。如果不能被16、8、4、2、1位表示，那么“右移16、8、4、2、1位之后两次逻辑取非的结果”就会是0；如果能被16、8、4、2、1位表示，那么“右移16、8、4、2、1位之后两次逻辑取非的结果”就会是1。同样也只有不能被16、8、4、2、1位表示的时候，才需要把temp的高位移到低位，此时“右移16、8、4、2、1位之后两次逻辑取非的结果”就会是1，让temp右移“右移16、8、4、2、1位之后两次逻辑取非的结果”，也正好实现了把temp的高位移到低位。代码如 图1：编写第15个函数howManyBits 所示。检查该函数的过程如 图2：检查第15个函数howManyBits 所示。

    int temp = x ^ (x << 1);
    int bit_16,bit_8,bit_4,bit_2,bit_1;
    bit_16 = !!(temp >> 16) << 4;
    temp = temp >> bit_16;
    bit_8 = !!(temp >> 8) << 3;
    temp = temp >> bit_8;
    bit_4 = !!(temp >> 4) << 2;
    temp = temp >> bit_4;
    bit_2 = !!(temp >> 2) << 1;
    temp = temp >> bit_2;
    bit_1 = !!(temp >> 1);
    return 1 + bit_1 + bit_2 + bit_4 + bit_8 + bit_16;

（图1：编写第15个函数howManyBits）

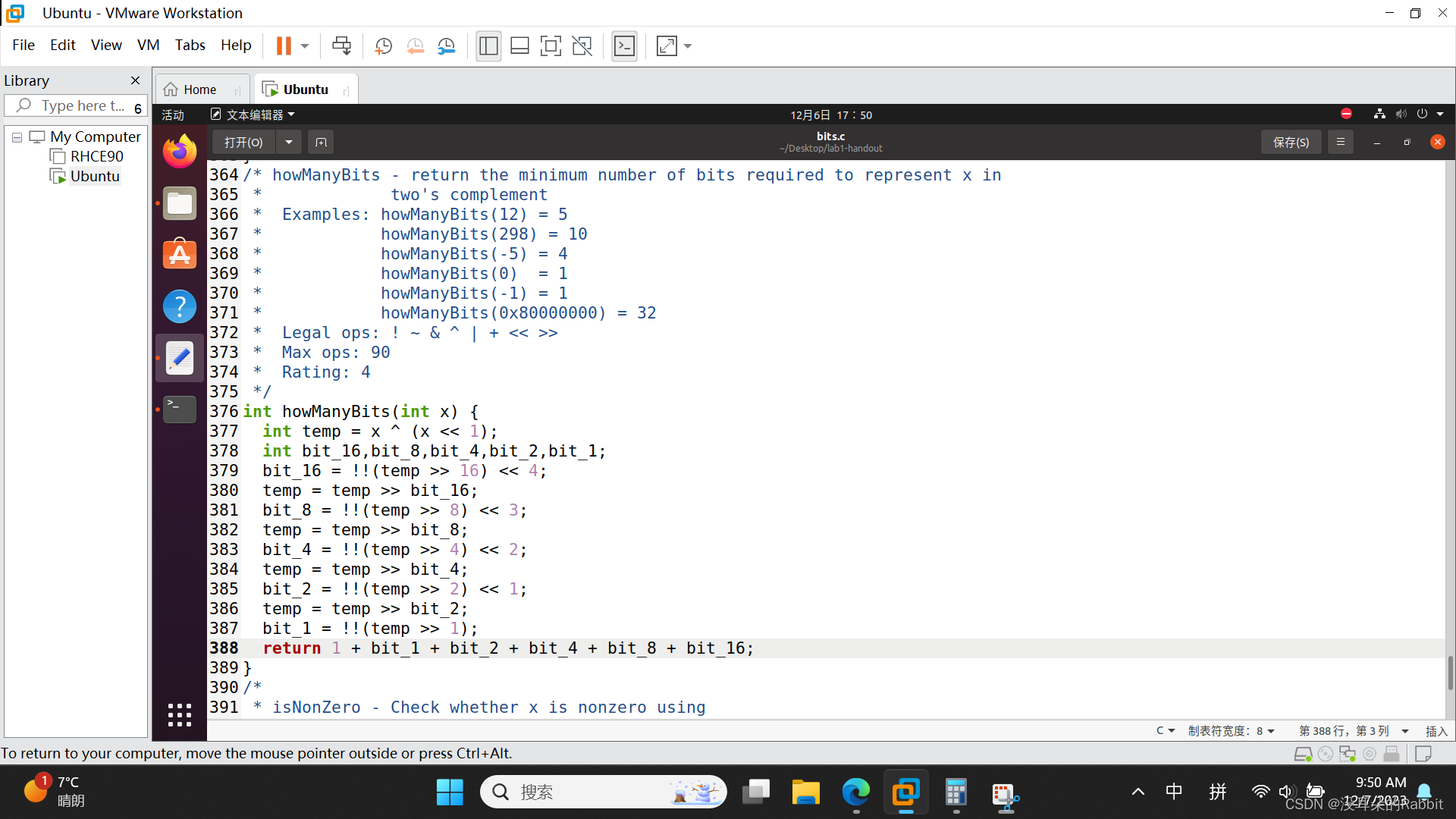
（图2：检查第15个函数howManyBits）

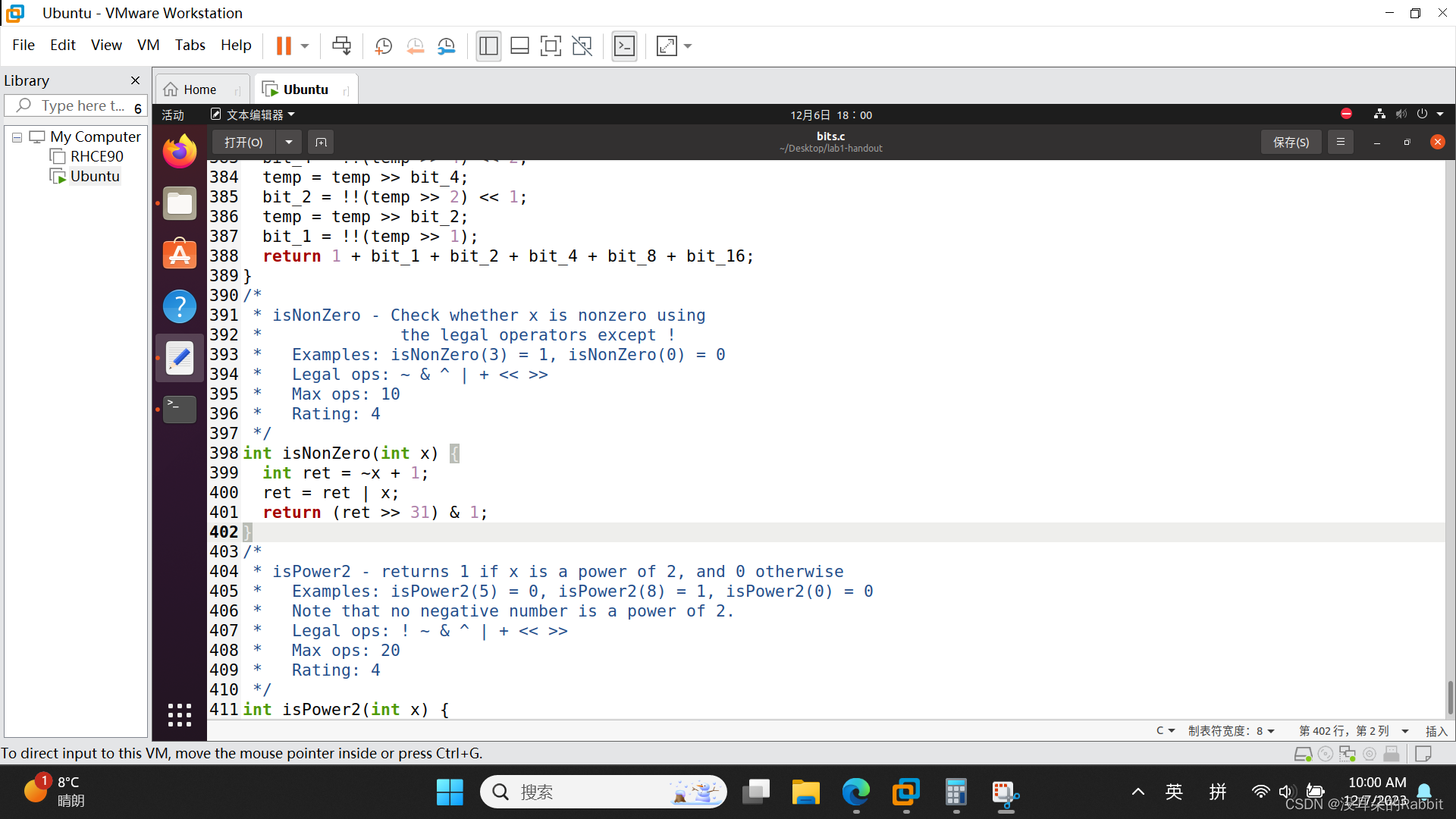
接着第16个函数，isNonZero，不使用逻辑非运算符！，检查x是否非0，比如isNonZero(3) = 1, isNonZero(0) = 0。怎么办呢？想一想发现，除了0之外，+1和-1位或的结果为0xFFFF FFFF，+2与-2位或的结果也是0xFFFF FFFF，+3与-3位或的结果也是0xFFFF FFFF... ...+2147483627与-2147483647位或的结果还是0xFFFF FFFF，甚至-2147483648与+2147483648（虽然不存在）位或的结果也还是0xFFFF FFFF，而+0与-0位或的结果却是0。利用这个性质，我们可以写出如 图3：编写第16个函数isNonZero 所示的代码。检查第16个函数的过程如 图4：检查第16个函数isNonZero 所示。

  int ret = ~x + 1;  
  ret = ret | x;       
  return (ret >> 31) & 1;

（图3：编写第16个函数isNonZero）

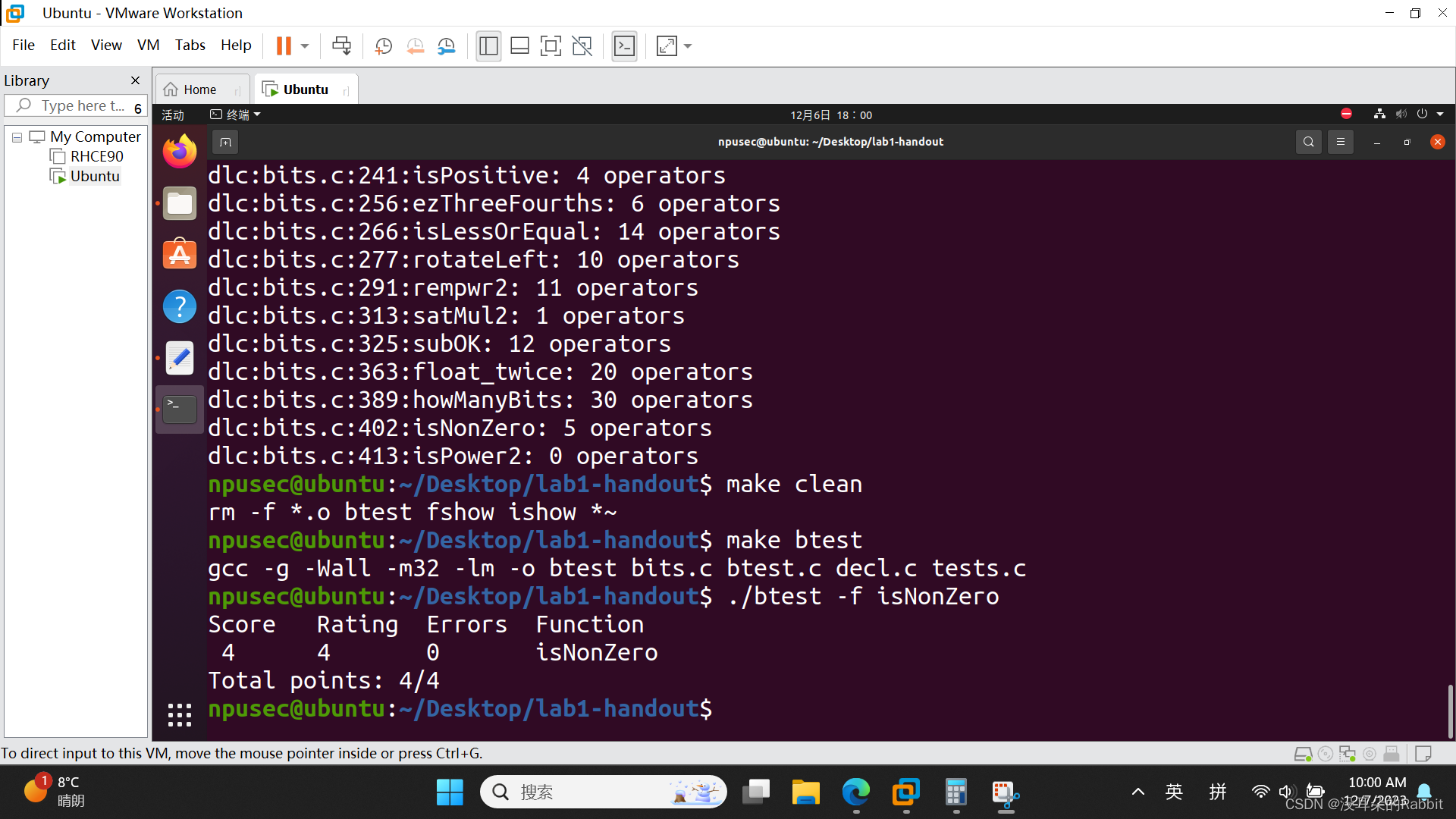
（图4：检查第16个函数isNonZero）

第17个函数，isPower2，判断x是不是2的1、2、3、4... ...次幂，如果是的话，返回1，否则返回0。我们该怎么做这道题呢？注意没有负数是2的多少次幂。顺着这个思路，我们首先排除0和负数，排除0可以用!!x表示，排除负数可以用!(x>>31)表示。这时如何判断x是不是2的1、2、3、4... ...次幂呢？我们关注这些数的性质，0x0000 8000，0x0000 4000，我们发现其仅有除第一位以外的一位为1，其余位全部为0，这些数加上0xFFFF FFFF之后的结果，与这些本身位与的结果一定为0，而其它数加上0xFFFF FFFF之后再与本身位与的结果必不为0。所以我们可以利用这个性质，写出表达式!(x&(x+~0))。最终的代码如 图5：编写第17个函数isPower2 所示，检查过程如 图6：检查第17个函数isPower2 所示。

  int y = x+~0;
  return !(x&y)&!(x>>31)&!!x;

（图5：编写第17个函数isPower2）

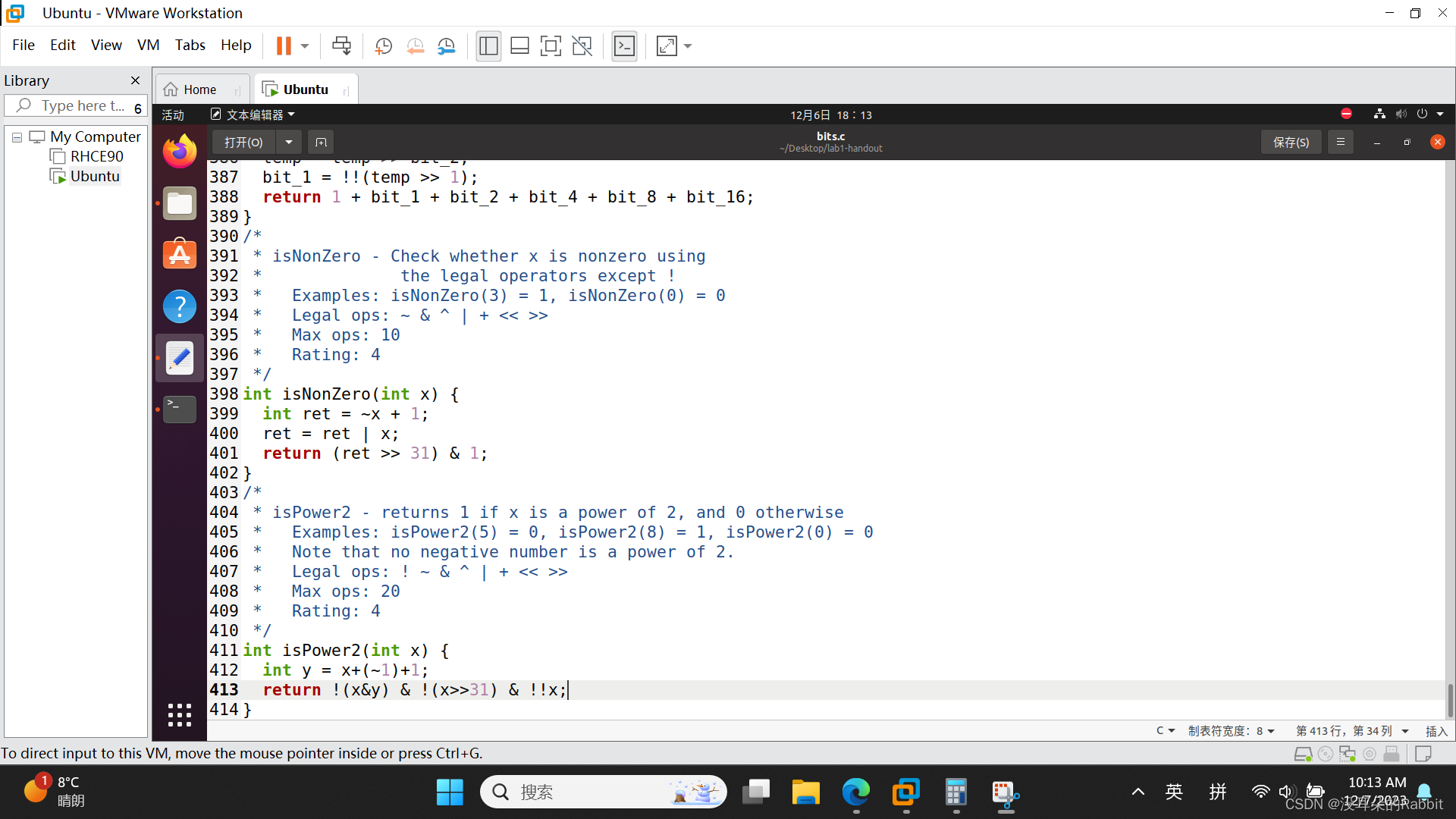
（图6：检查第17个函数isPower2）

/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  int temp = x ^ (x << 1);
  int bit_16,bit_8,bit_4,bit_2,bit_1;
  bit_16 = !!(temp >> 16) << 4;
  temp = temp >> bit_16;
  bit_8 = !!(temp >> 8) << 3;
  temp = temp >> bit_8;
  bit_4 = !!(temp >> 4) << 2;
  temp = temp >> bit_4;
  bit_2 = !!(temp >> 2) << 1;
  temp = temp >> bit_2;
  bit_1 = !!(temp >> 1);
  return 1 + bit_1 + bit_2 + bit_4 + bit_8 + bit_16;
}
/* 
 * isNonZero - Check whether x is nonzero using
 *              the legal operators except !
 *   Examples: isNonZero(3) = 1, isNonZero(0) = 0
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 10
 *   Rating: 4 
 */
int isNonZero(int x) {
  int ret = ~x + 1;  
  ret = ret | x;       
  return (ret >> 31) & 1;
}
/*
 * isPower2 - returns 1 if x is a power of 2, and 0 otherwise
 *   Examples: isPower2(5) = 0, isPower2(8) = 1, isPower2(0) = 0
 *   Note that no negative number is a power of 2.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 20
 *   Rating: 4
 */
int isPower2(int x) {
  int y = x+(~1)+1;
  return !(x&y) & !(x>>31) & !!x;
}