目录
一.双向链表的概念
二.双向链表的数据结构
三.双向链表的实现
节点的插入
头插法
尾插法
任意位置插入
节点的删除
删除链表中第一次出现的目标节点
删除链表中所有与关键字相同的节点
节点的查找
链表的清空
链表的长度
四.模拟实现链表的完整代码
前言：在上一篇文章中，我们认识了链表中的单链表，而本篇文章则是介绍线链表中的另一个结构双向链表，有兴趣的朋友们可以点击了解：图文详解单链表的各种操作
一.双向链表的概念
双向链表（Doubly Linked List）是一种数据结构，它与单向链表相似，但每个节点不仅包含指向下一个节点的指针，还包含指向上一个节点的指针。
双向链表的每个节点通常包含以下两个指针：
- prev：指向上一个节点
- next：指向下一个节点
通过这两个指针，可以在双向链表中沿着两个方向遍历。
相比于单向链表，双向链表能够更方便地进行插入和删除操作。因为每个节点包含指向前一个节点的指针，所以在删除或插入一个节点时，只需要修改该节点前后节点的指针即可。而在单向链表中，则需要在删除或插入节点时，找到该节点的前一个节点，以便进行指针修改，显得相对麻烦。
二.双向链表的数据结构
双向俩表有俩个指针，分别存放前驱节点的地址和后继节点的地址，如图所示
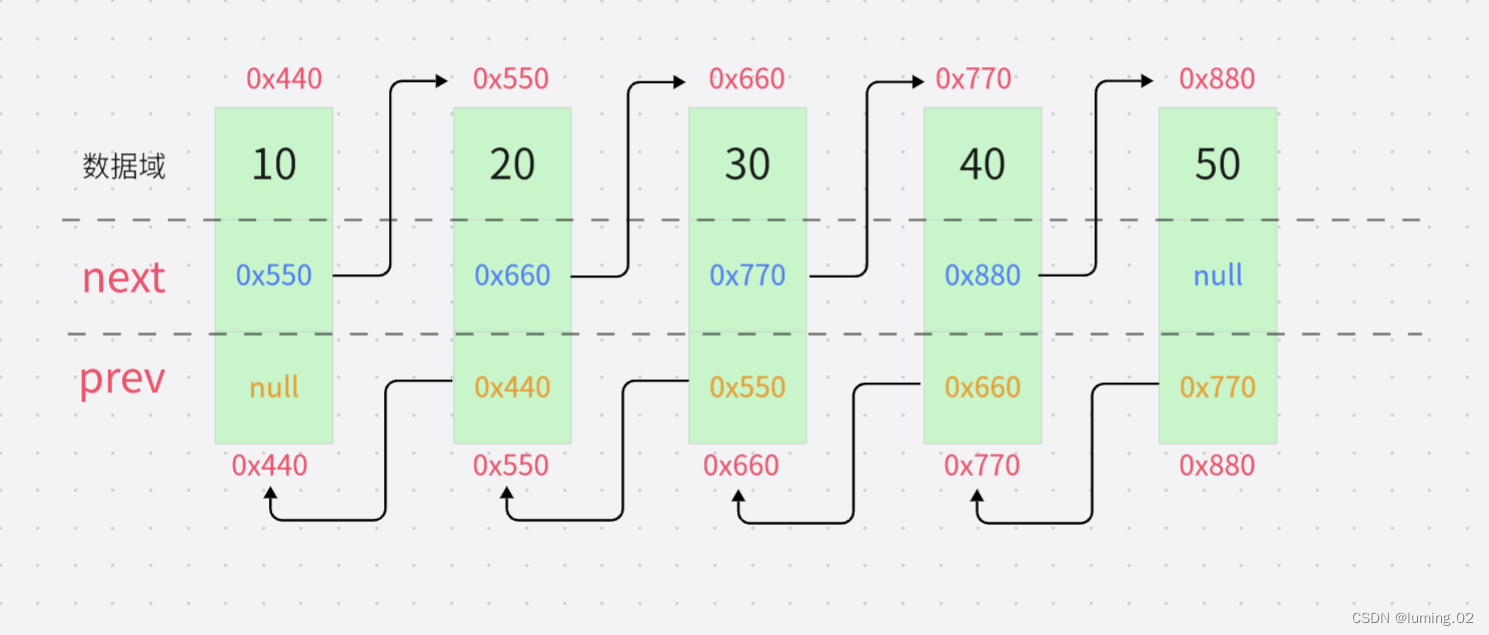
对于其中每一个节点，我们可以如下存储
public class Node{
public int data;
public Node prev;
public Node next;
//构造方法，给每个节点赋值
public Node(int data) {
this.data = data;
}
}而我们的链表则是需要将所有的节点封装起来，放进一个数据结构中，因此将刚才定义的节点类作为链表的内部类即可，而链表又需要实现各种各样的功能，我们可以将所有的链表的功能抽象出一个接口，然后通过链表去具体的实现那些功能
public class MyLinkList implements Ilst{
//节点的数据结构
public class Node{
public int data;
public Node prev;
public Node next;
//构造方法
public Node(int data) {
this.data = data;
}
}
public Node head;//头节点
public Node last;//尾节点
}接口：
public interface Ilst {
//头插法
public void addFirst(int data);
//尾插法
public void addLast(int data);
//任意位置插入
public void addIndex(int index,int data);
//查找是否包含关键字key是否在链表当中
public boolean contains(int key);
//删除第一次出现关键字为key的节点
public void remove(int key);
//删除所有值为key的节点
public void removeAllKey(int key);
//得到链表的长度
public int size();
//展示链表
public void display();
//清空链表
public void clear();
}
三.双向链表的实现
节点的插入
节点的插入分为三种情况，一是在链表最前面进行插入也就是头插法，二是在链表末尾进行插入，也就是尾插法，三是在链表中间位置插入
头插法
如图所示有一个新的节点，我们需要将其插入头节点的位置
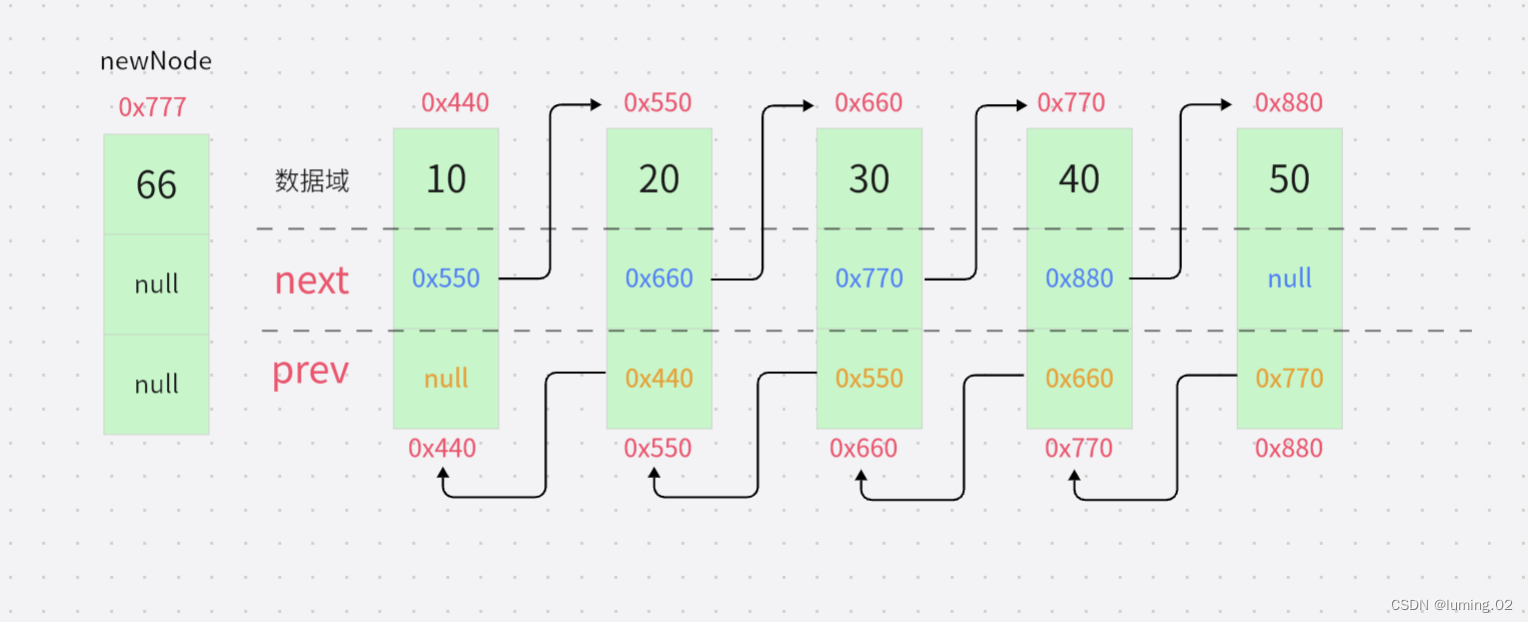
第一步：将目标节点的后继指针指向头节点位置的节点
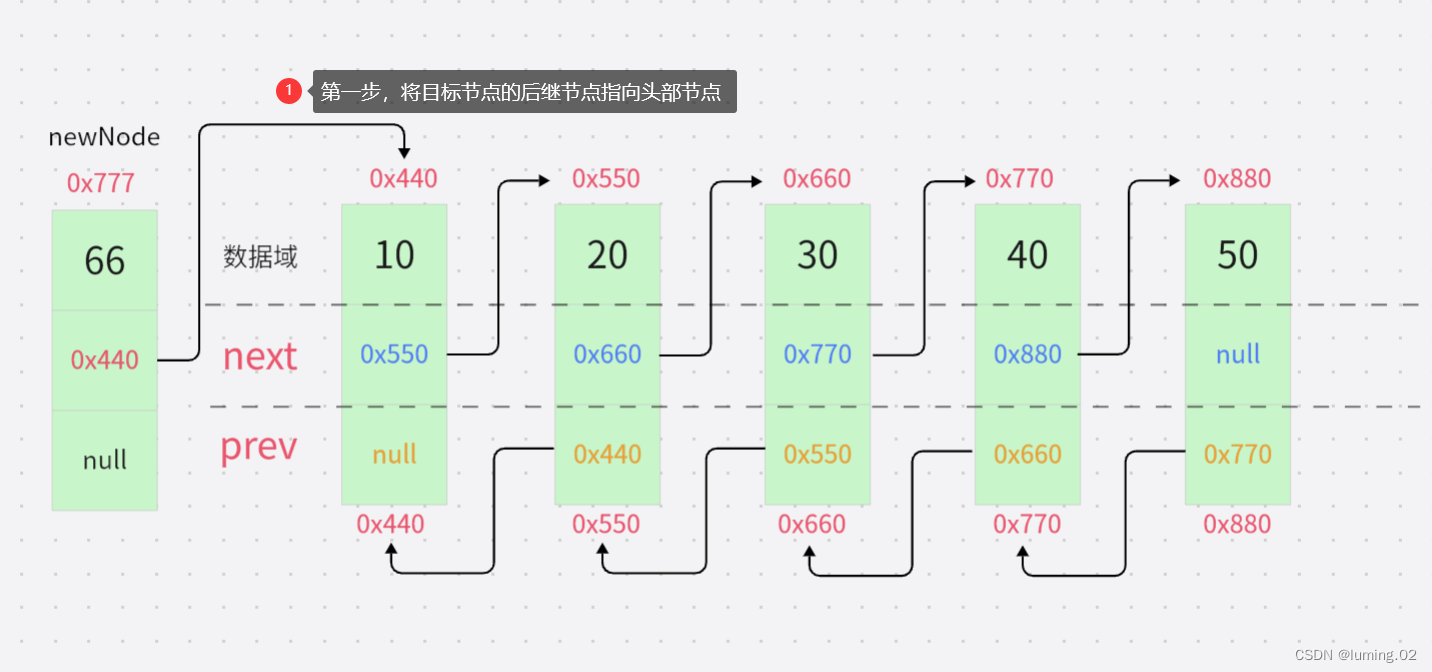
第二步，将头节点的前驱指针指向目标节点
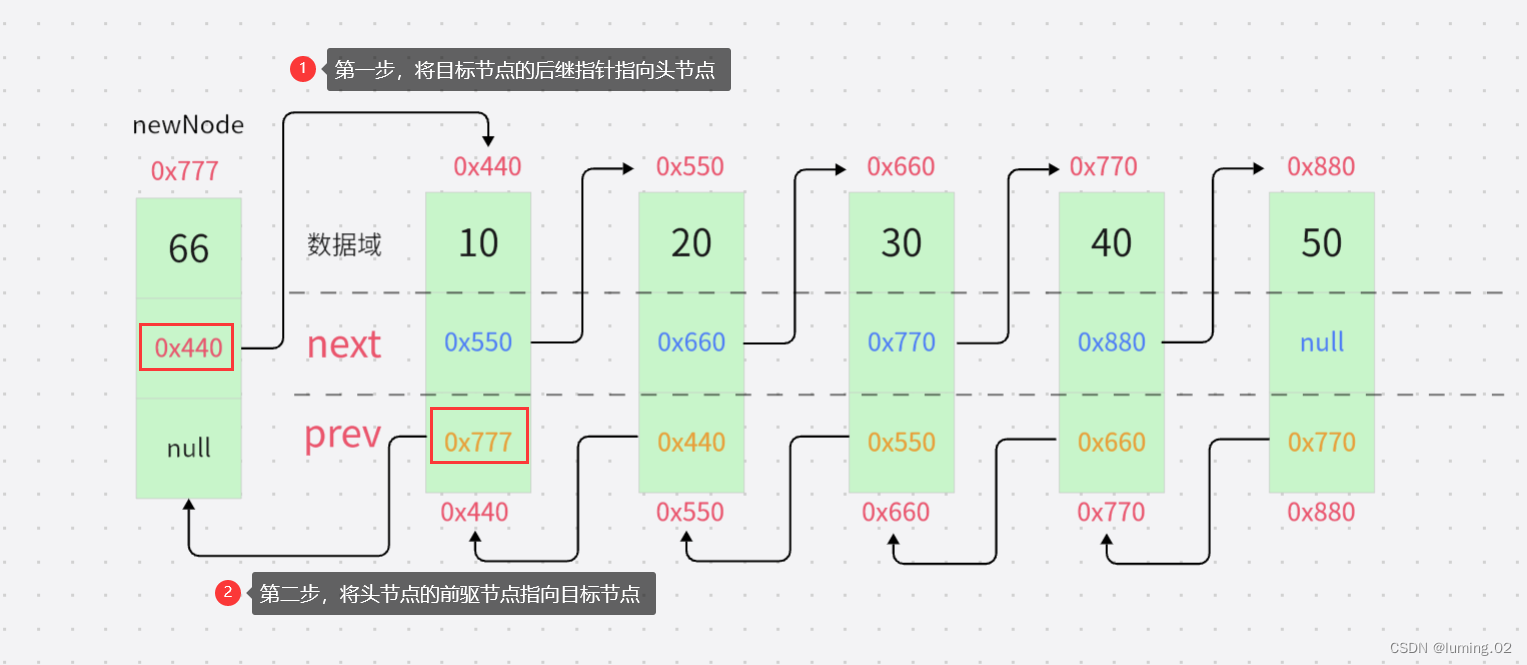
在使用代码具体实现的时候，需要对异常做出判断，假如头节点为空，也就是链表里面没有节点的时候，我们就直接让我们要新加的节点既是头节点，又是尾节点；在做出异常处理后，我们就可以按照刚才图示的过程进行头插了，但是需要注意的是，在完成头插后需要更新头节点的位置
@Override//头插法
public void addFirst(int data) {
Node newNode = new Node(data);
if (head == null){
head = newNode;
last = newNode;
}else {
newNode.next = head;
head.prev = newNode;
//更新头节点
head = newNode;
}
}尾插法
如图所示有一个新的节点，我们需要将其插入链表的末尾
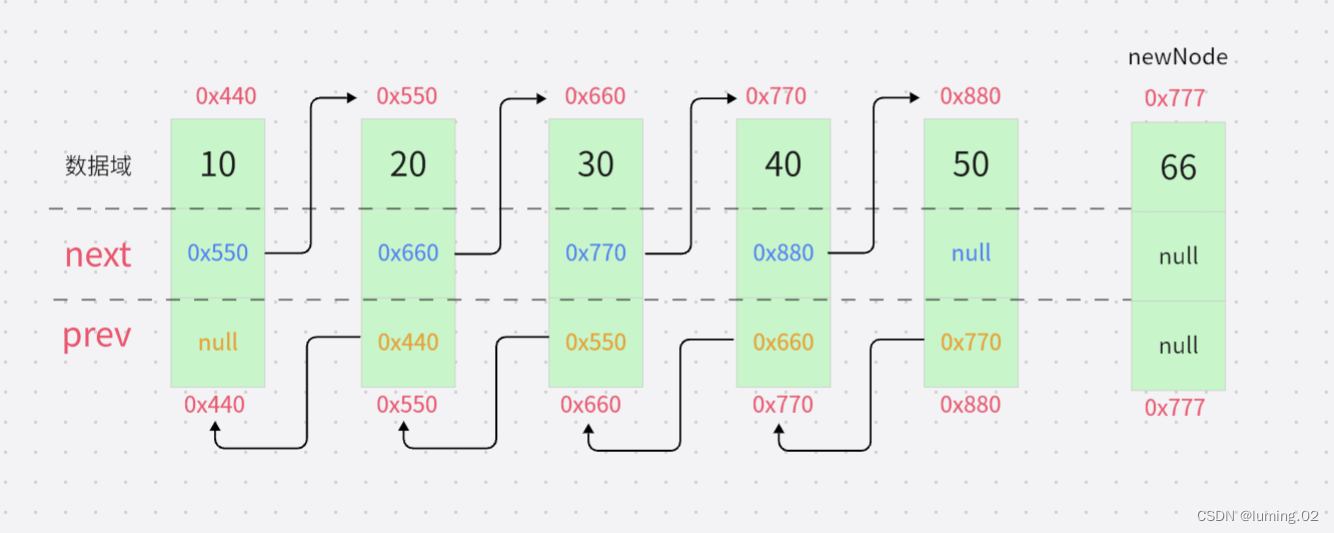
第一步：将目标节点的前驱指针指向尾部节点
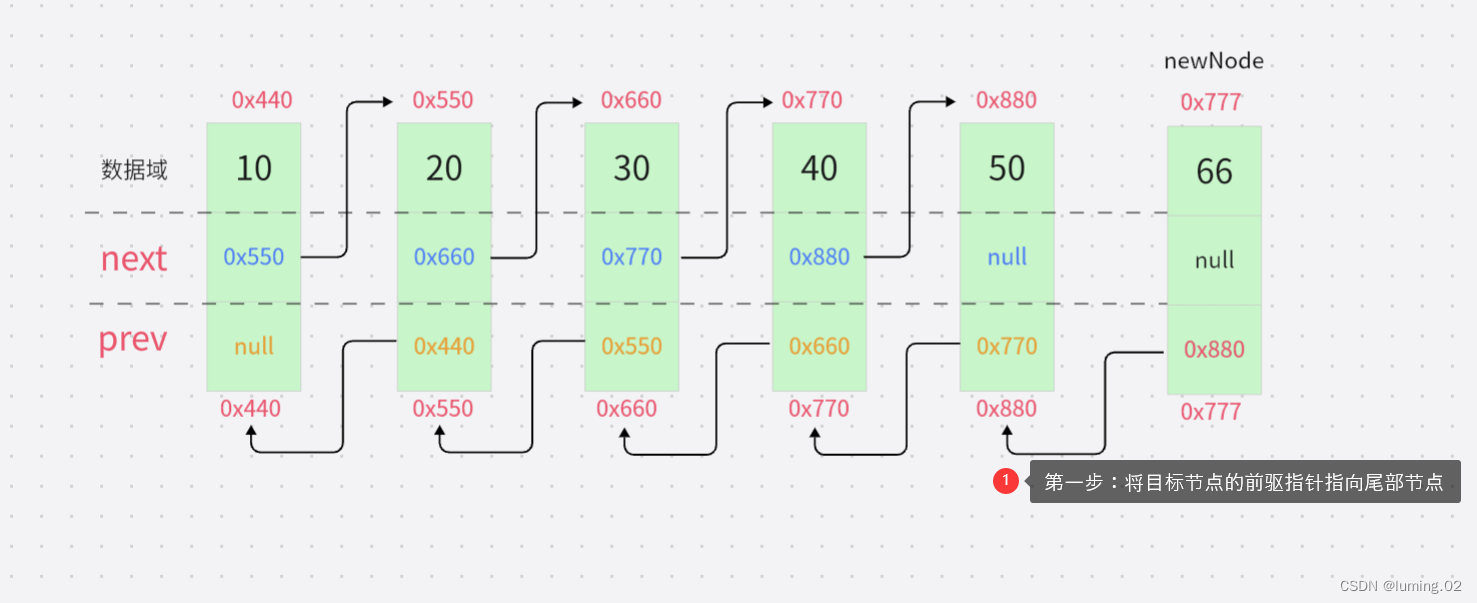
第二步：将尾部节点的后继指针指向目标节点
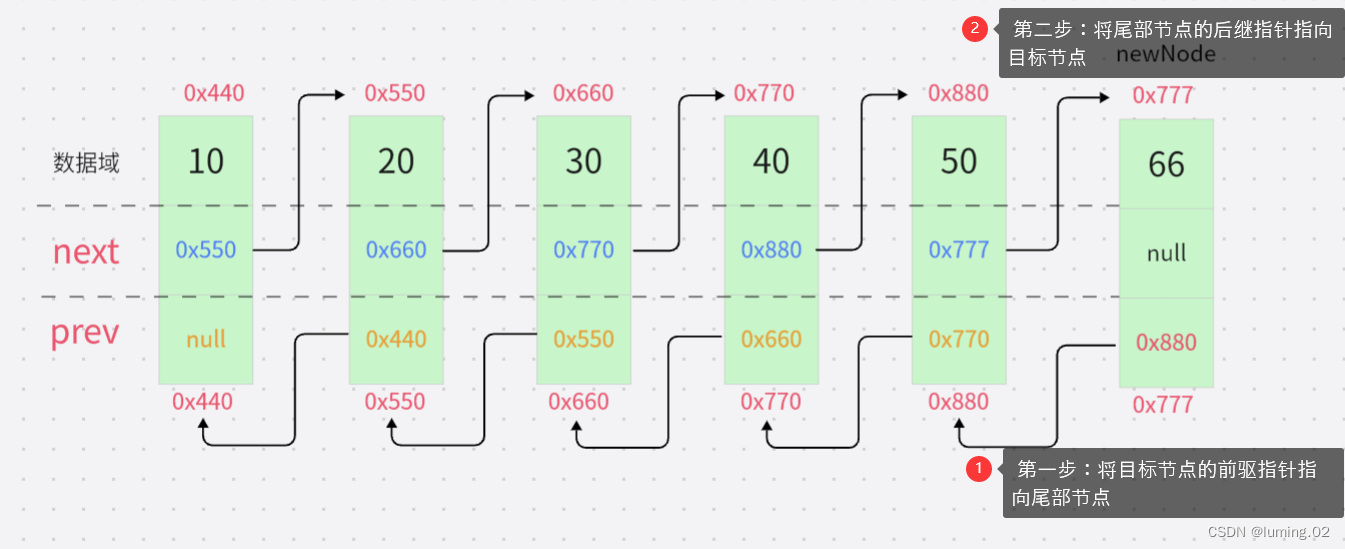
在使用代码具体实现的时候，需要对异常做出判断，假如头节点为空，也就是链表里面没有节点的时候，我们就直接让我们要新加的节点既是头节点，又是尾节点；在做出异常处理后，我们就可以按照刚才图示的过程进行尾插了，但是需要注意的是，在完成头插后需要更新尾部节点的位置
@Override//尾插法
public void addLast(int data) {
Node newNode = new Node(data);
if (head == null){
head = newNode;
last = newNode;
}else {
newNode.prev = last;
last.next = newNode;
//更新尾部节点
last = newNode;
}
}任意位置插入
如图，假如想让新节点插入第三个节点的位置，该如何做呢？
第一步：先将目标节点的后继指针指向要插入节点的后一个节点
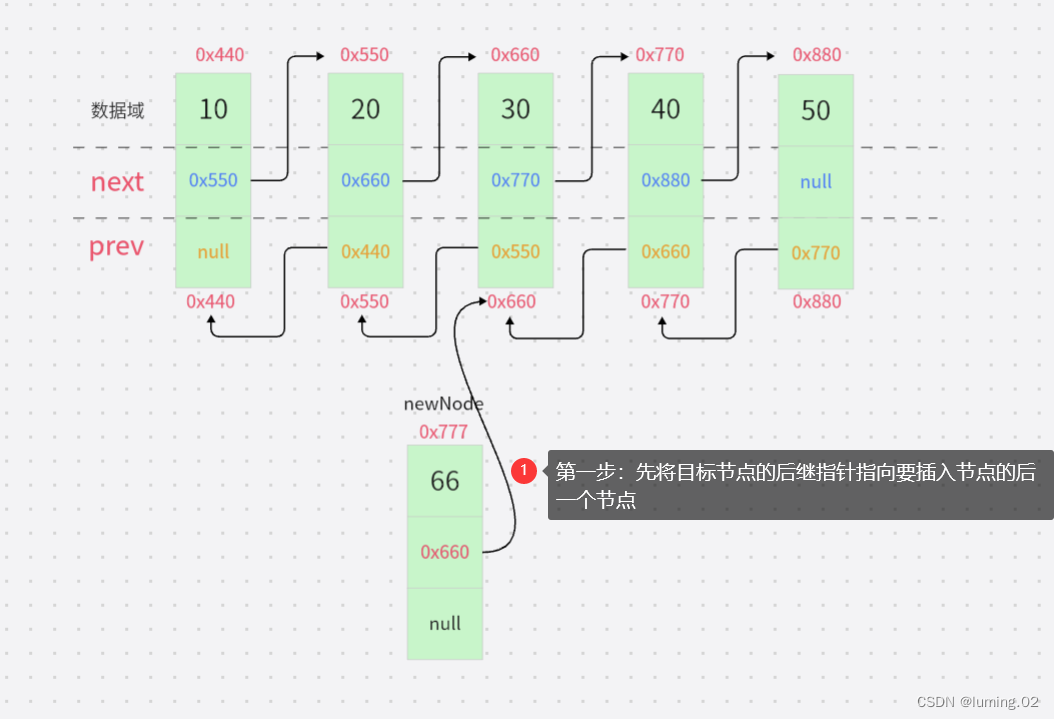
第二步：将目标节点的前驱指针指向插入节点
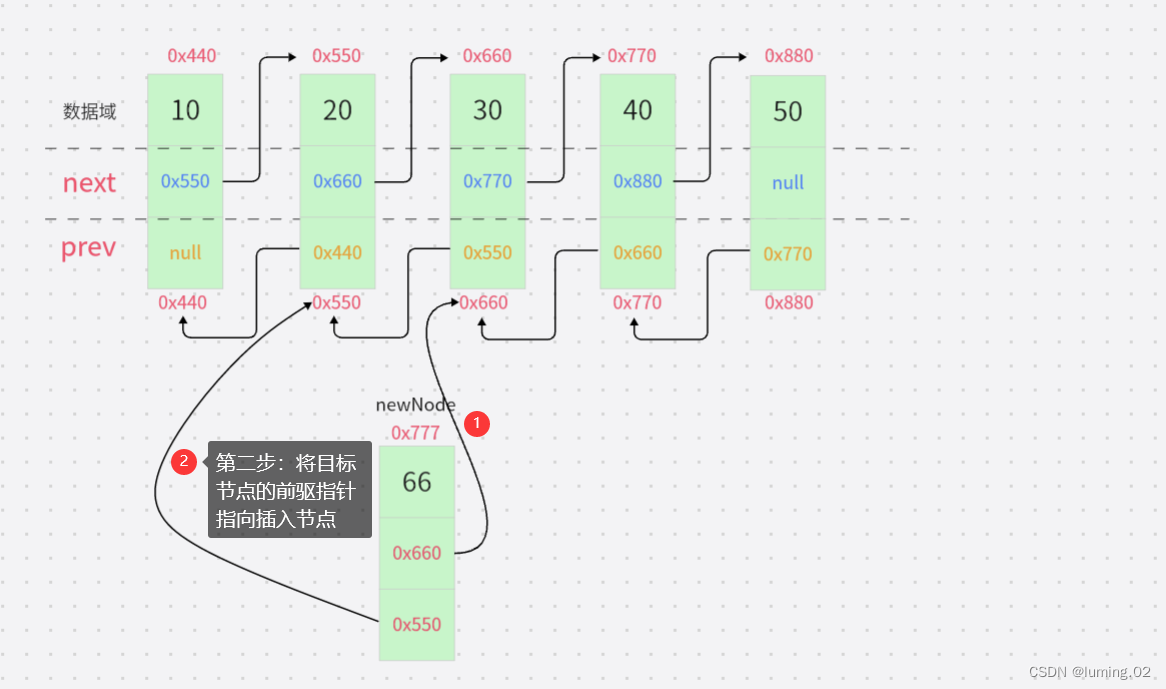
第三步：将插入节点的后继指针指向目标节点
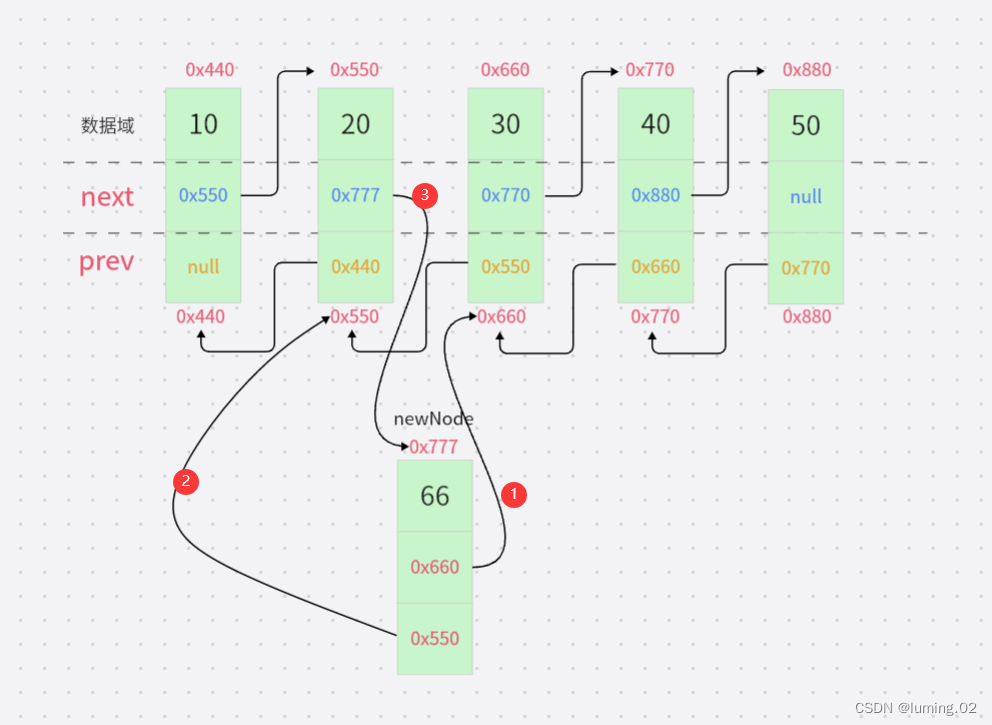
第四步：将插入节点的后一个节点的前驱指针指向目标节点
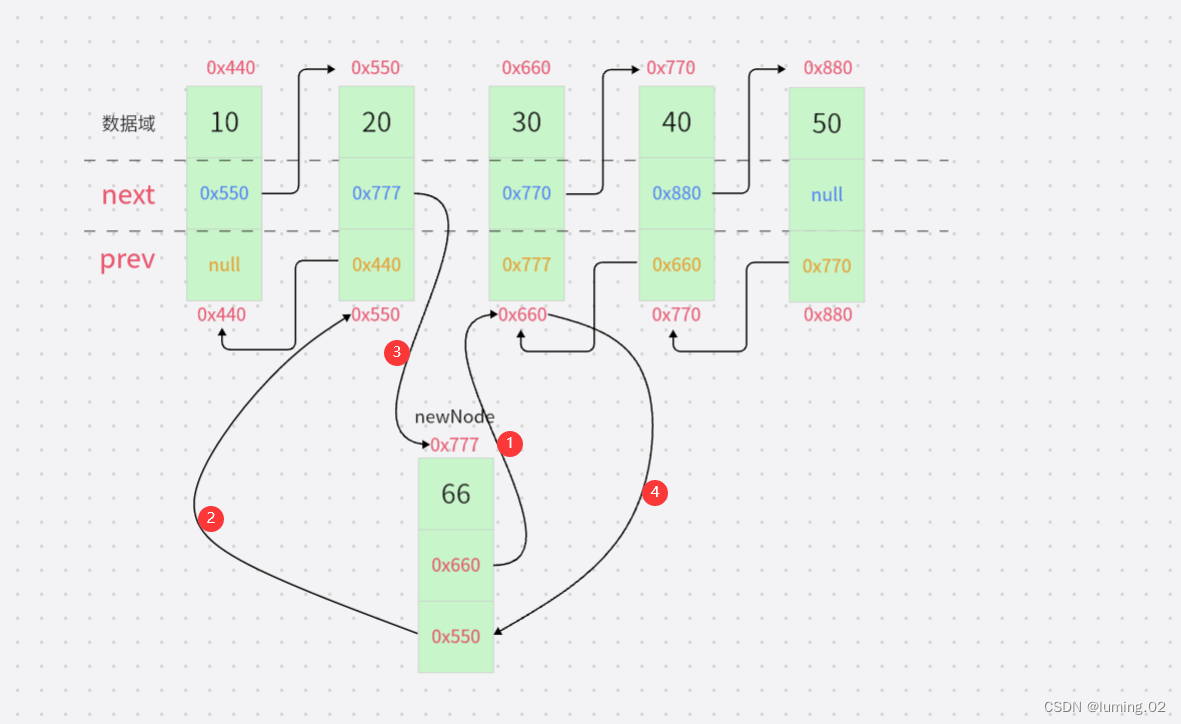
对于节点的插入，最难的一点便是这4个步骤的顺序，顺序不是一成不变也不必死背，只需要记住一个原则——保证链表不断，在这个原则的基础上进行操作就不会出现问题了，也就是说在我们插入的时候，不要因为先去处理前面的节点导致找不到后面的节点就可以，因此我们在对链表进行插入操作的时候，一般都习惯先对后面的节点进行操作。
对于输入的位置我们要进行合法性的判断，如果在最前面就刚好使用头插法，如果是最后面就使用尾插法，之后遍历找到我们要插入的位置
@Override//任意位置插入
public void addIndex(int index, int data) {
//对输入位置进行判断
if (index < 0 || index > size()) {
System.out.println("输入位置不合法");
return;
}
if (index == 0) {
//如果插入位置在最前面就使用头插
addFirst(data);
return;
}
if (index == size()) {//这里的size方法在后文中有定义
//如果插入位置在最后面就使用尾插
addLast(data);
return;
}
//在中间插入
Node newNode = new Node(data);
//找到要插入的位置
Node cur = head;
while (index != 1) {
cur = cur.next;
index--;
}
//将新节点插入到cur之前
newNode.next = cur;
newNode.prev = cur.prev;
cur.prev.next = newNode;
cur.prev = newNode;
// //将新节点插入到cur之后
// newNode.next = cur.next;
// newNode.prev = cur;
// cur.next = newNode;
// newNode.next.prev = newNode;
}节点的删除
对于节点的删除我们分为俩种，一种的将单个节点进行删除，一种是将所有与目标值相同的节点进行删除
删除链表中第一次出现的目标节点
如图，我们假定我们要删除链表中第三个节点
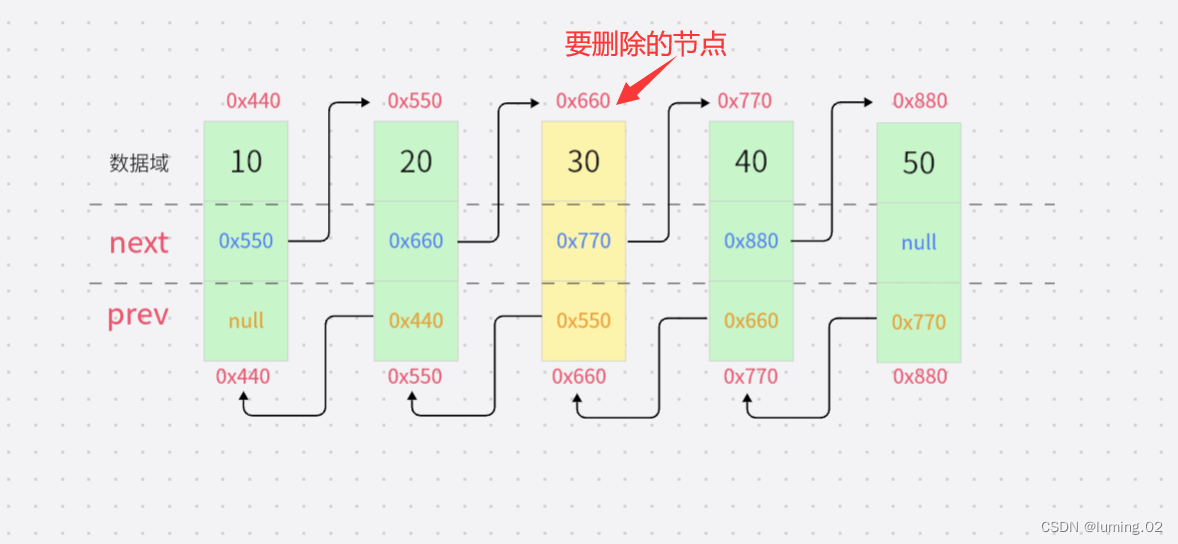
第一步：将删除节点的前驱节点的后继指针指向删除节点的后继节点
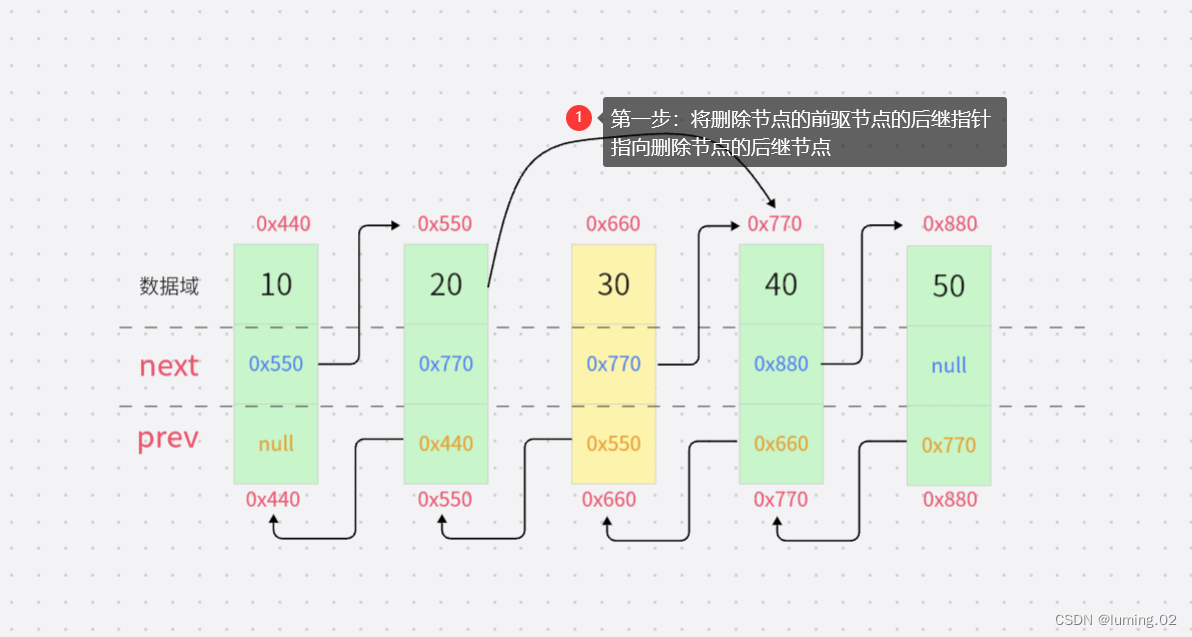
第二步：将删除节点的后继节点的前驱指针指向删除节点的前驱节点
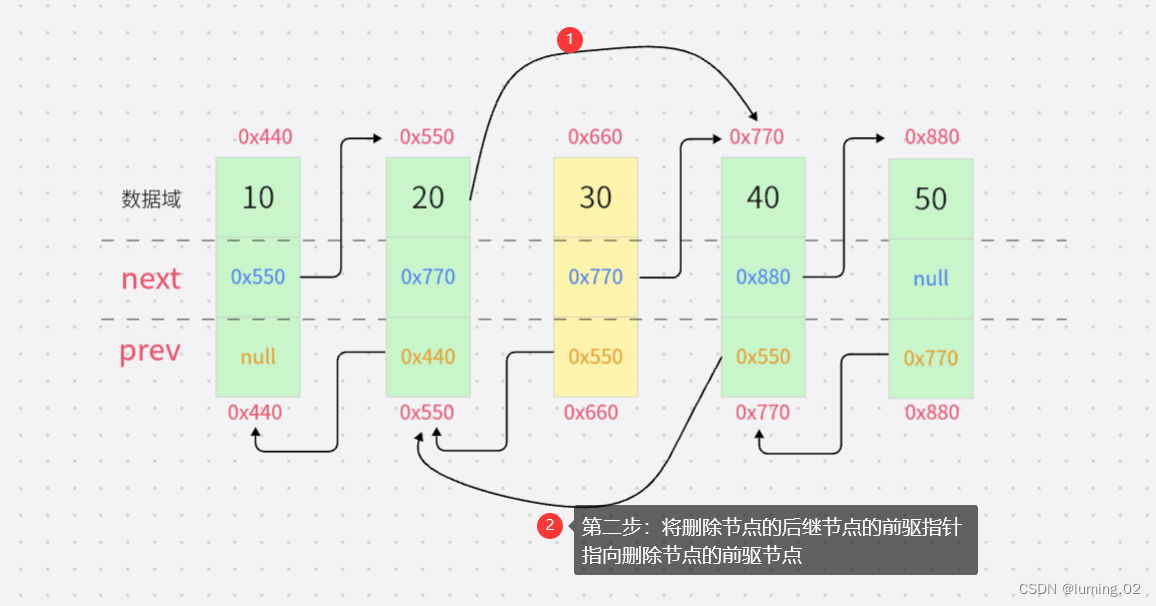
对于上面俩个过程只是俩行代码就可以解决：
cur.next.prev = cur.prev;
cur.prev.next = cur.next;删除的过程非常简单，但是要找到正确的位置并不是一件容易事，就算找到后也要进行合法性的判断，具体代码如下：
@Override//删除第一次出现关键字为key的节点
public void remove(int key) {
Node cur = head;
while (cur != null) {
if(cur.data == key) {
if(cur == head) {
head = head.next;
if(head != null) {
head.prev = null;
}else {
//只有一个节点 且是需要删除的节点
last = null;
}
}else {
if(cur.next != null) {
//删除中间节点
cur.next.prev = cur.prev;
cur.prev.next = cur.next;
}else {
//删除尾巴节点
cur.prev.next = cur.next;
last = last.prev;
}
}
return;
}
cur = cur.next;
}
}删除链表中所有与关键字相同的节点
对于和刚才唯一不同的点就是我们在删除一个点后不需要停止返回，继续遍历整个链表进行删除即可，这里就不再赘述
@Override//删除所有值为key的节点
public void removeAllKey(int key) {
Node cur = head;
while (cur != null) {
if(cur.data == key) {
if(cur == head) {
head = head.next;
if(head != null) {
head.prev = null;
}else {
//只有一个节点 且是需要删除的节点
last = null;
}
}else {
if(cur.next != null) {
//删除中间节点
cur.next.prev = cur.prev;
cur.prev.next = cur.next;
}else {
//删除尾巴节点
cur.prev.next = cur.next;
last = last.prev;
}
}
}
cur = cur.next;
}
}节点的查找
对于节点的查找，只需要挨个遍历判断就可以
@Override//查找是否包含关键字key是否在链表当中
public boolean contains(int key) {
Node cur = head;
while (cur != null){
if (cur.data == key){
return true;
}else {
cur = cur.next;
}
}
return false;
}链表的清空
清空链表需要对每个节点进行清空，因此我们遍历整个链表然后进行赋值为空就可以，但是有一点需要注意，我们在删除每一个节点的后继指针之前得先做临时的记录，不然我们删除了一个节点的后继指针后就无法通过它访问后一个节点了
@Override//清空链表
public void clear() {
Node cur = head;
while (cur != null){
Node tempNode = cur.next;//记录当前节点的下一个节点的地址
cur.prev = null;
cur.next = null;
cur = tempNode;
}
this.head = null;
this.last = null;
}链表的长度
求链表的长度只需要使用计数器遍历累加就可以
@Override//得到单链表的长度
public int size() {
int count = 0;
Node cur = head;
while (cur != null) {
count++;
cur = cur.next;
}
return count;
}四.模拟实现链表的完整代码
package MyLinkList;
public class MyLinkList implements Ilst {
public class Node {
public int data;
public Node prev;
public Node next;
//构造方法
public Node(int data) {
this.data = data;
}
}
public Node head;
public Node last;
@Override//头插法
public void addFirst(int data) {
Node newNode = new Node(data);
if (head == null) {
head = newNode;
last = newNode;
} else {
newNode.next = head;
head.prev = newNode;
//更新头节点
head = newNode;
}
}
@Override//尾插法
public void addLast(int data) {
Node newNode = new Node(data);
if (head == null) {
head = newNode;
last = newNode;
} else {
newNode.prev = last;
last.next = newNode;
//更新尾部节点
last = newNode;
}
}
@Override//任意位置插入
public void addIndex(int index, int data) {
//对输入位置进行判断
if (index < 0 || index > size()) {
System.out.println("输入位置不合法");
return;
}
if (index == 0) {
//如果插入位置在最前面就使用头插
addFirst(data);
return;
}
if (index == size()) {
//如果插入位置在最后面就使用尾插
addLast(data);
return;
}
//在中间插入
Node newNode = new Node(data);
//找到要插入的位置
Node cur = head;
while (index != 1) {
cur = cur.next;
index--;
}
//将新节点插入到cur之前
newNode.next = cur;
newNode.prev = cur.prev;
cur.prev.next = newNode;
cur.prev = newNode;
// //将新节点插入到cur之后
// newNode.next = cur.next;
// newNode.prev = cur;
// cur.next = newNode;
// newNode.next.prev = newNode;
}
@Override//查找是否包含关键字key是否在链表当中
public boolean contains(int key) {
Node cur = head;
while (cur != null){
if (cur.data == key){
return true;
}else {
cur = cur.next;
}
}
return false;
}
@Override//删除第一次出现关键字为key的节点
public void remove(int key) {
Node cur = head;
while (cur != null) {
if(cur.data == key) {
if(cur == head) {
head = head.next;
if(head != null) {
head.prev = null;
}else {
//只有一个节点 且是需要删除的节点
last = null;
}
}else {
if(cur.next != null) {
//删除中间节点
cur.next.prev = cur.prev;
cur.prev.next = cur.next;
}else {
//删除尾巴节点
cur.prev.next = cur.next;
last = last.prev;
}
}
return;
}
cur = cur.next;
}
}
@Override//删除所有值为key的节点
public void removeAllKey(int key) {
Node cur = head;
while (cur != null) {
if(cur.data == key) {
if(cur == head) {
head = head.next;
if(head != null) {
head.prev = null;
}else {
//只有一个节点 且是需要删除的节点
last = null;
}
}else {
if(cur.next != null) {
//删除中间节点
cur.next.prev = cur.prev;
cur.prev.next = cur.next;
}else {
//删除尾巴节点
cur.prev.next = cur.next;
last = last.prev;
}
}
}
cur = cur.next;
}
}
@Override//得到单链表的长度
public int size() {
int count = 0;
Node cur = head;
while (cur != null) {
count++;
cur = cur.next;
}
return count;
}
@Override//展示链表
public void display() {
Node cur = head;
while (cur != null) {
System.out.print(cur.data + " ");
cur = cur.next;
}
System.out.println();
}
@Override//清空链表
public void clear() {
Node cur = head;
while (cur != null){
Node tempNode = cur.next;
cur.prev = null;
cur.next = null;
cur = tempNode;
}
this.head = null;
this.last = null;
}
}
本次的分享就到此为止了，希望我的分享能给您带来帮助，也欢迎大家三连支持，你们的点赞就是博主更新最大的动力！
如有不同意见，欢迎评论区积极讨论交流，让我们一起学习进步！
有相关问题也可以私信博主，评论区和私信都会认真查看的，我们下次再见
![sql注入 [GXYCTF2019]BabySQli1](https://img-blog.csdnimg.cn/direct/459cdd2498e74a2b8ab050b33a6dfcc4.png)
