目录
一、课题描述
输入样例:
输出样例:
二、需求分析
输入的形式和输入值的范围:
输出的形式:
程序所能达到的功能:
三、概要设计
四、流程图
五 、代码+详细注释
六、测试数据和结果
一、课题描述
以一个 m*n 的方阵表示迷宫,0 和 1 分别表示迷宫中的通路和障碍。设计一个程序,对任意设定的迷宫,求出一条从入口到出口的最短通路,或得出没有通路的结论。
输入样例:
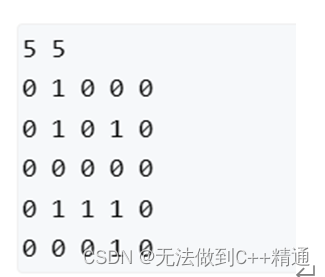
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0
输出样例:
8二、需求分析
本设计程序用C++ 编写,完成二维数组迷宫的生成,找到走出迷宫的最短路径,或者返回没有通路的结论。
-
输入的形式和输入值的范围:
- 输入格式:第一行包含两个整数 n 和 m。接下来 n行,每行包含 m 个整数(0 或 1),表示完整的二维数组迷宫。数据范围:1≤n,m≤100。
-
输出的形式:
- 输出一个整数,表示从左上角移动至右下角的最少移动次数。
程序所能达到的功能:
1.找到一条从入口到出口的最短通路2.如果迷宫内没有通路,则返回没有通路的结论。
三、概要设计
1 )数据逻辑结构、存储结构分析:
(1 ) 数据逻辑结构:
在迷宫求解的问题中,我运用了队列这种线性结构来存储最新到达的地点,队头出队即表示该点走向下一个结点。
(2 )存贮结构分析:
在迷宫求解的问题中,我运用了队列这种顺序结构,队列在这个代码中的作用是实现广度优先搜索算法(BFS)。BFS是一种图遍历算法,用于在图或二维网格中寻找最短路径或解决某些问题。
2 )本程序包含2 个函数:
(1 )广度优先搜索算法函数bfs()
- 参数描述:
g[N][N]:存贮迷宫信息
d[N][N]:存贮各个点到起始点的路径长度
PII q[N*N],hh,tt:模拟队列,PII q[N*N]:存贮队列中的数据,hh:队头,tt:队尾
Dx:代表这个点在x轴的偏移量,dy:代表这个点在y轴的偏移量
- 功能描述
初始化队列:将起始点排入队列中,即{0,0}。
初始化d数组:将d数组初始化为-1,从而在bfs搜索时能判断出这个点是否被搜索过
初始化dx数组和dy数组:即存贮x和y上下左右移动时的偏移量
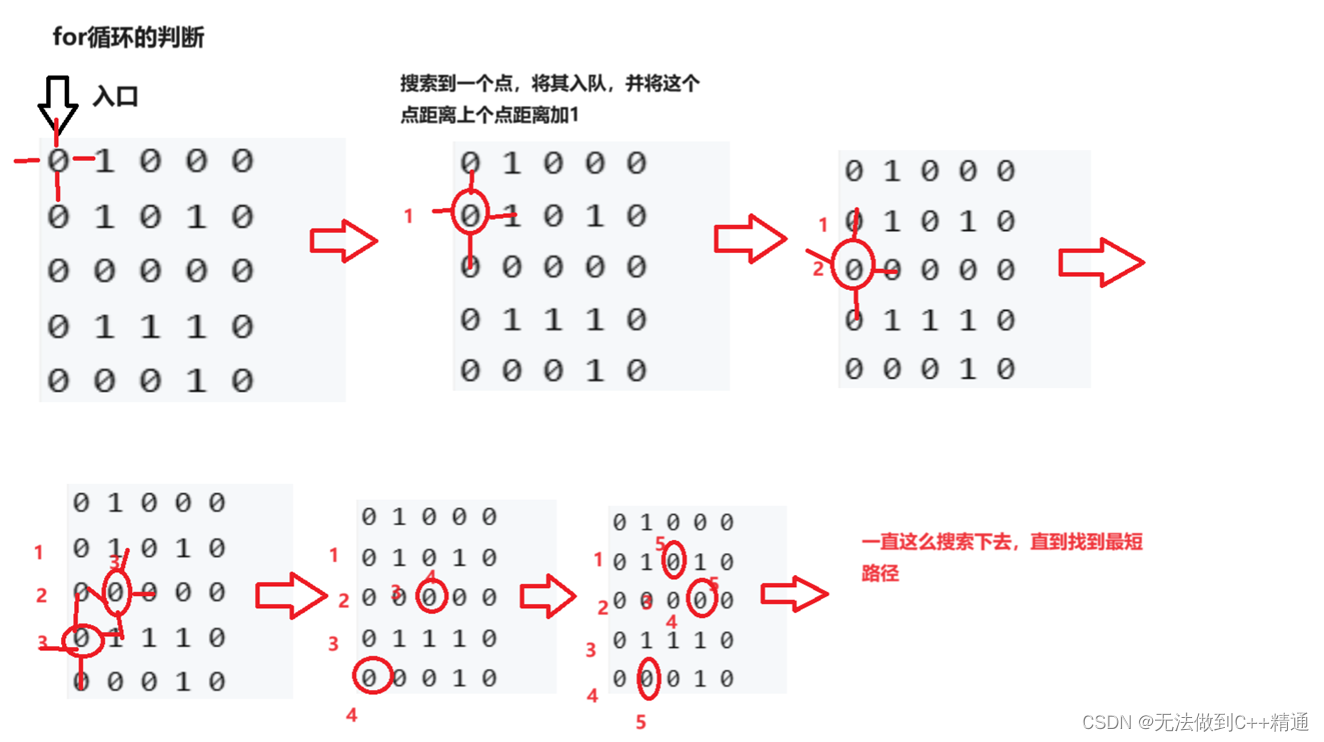
For循环判断:将这个点进行上下左右四次移动,如果它在我的二维数组迷宫里面(未超出范围)并且移动之后点的值等于0(能够通行)而且是第一次通过(最短路),我就将它入队,并且记录它距离下一个点的距离加1,然后就是一个循环过程,只要我的队里有元素,就说明还未找到最短路。
(2 )主函数main()
- 参数描述
M,n:代表m行n列的迷宫
Flag:判断迷宫中是否有通路
- 功能描述
初始化迷宫:输入m行n列的迷宫
判断返回值:将bfs得到的结果进行判断,如果我的迷宫出口距离起始点不是-1的话(已经被搜索到过),那我就返回最短路径,否则返回没有通路。
四、流程图

 五 、代码+详细注释
五 、代码+详细注释
#include <iostream>
#include <algorithm>
#include <cstdio>
using namespace std;
typedef pair<int, int>PII;
const int N = 110;
//定义一些全局变量
//n,m n行m列
//g数组 存贮迷宫
//d数组 存贮点到起始点的距离
//q二元组 存贮队列元素点的数据
int n, m;
int g[N][N];
int d[N][N];
PII q[N * N];
//重点!bfs的实现
int bfs()
{
//队头hh,队尾tt
int hh = 0, tt = 0;
//队头起始点{0,0}
q[0] = { 0,0 };
//memset函数,将d数组初始化为-1,主要是用于后面判断此点是否被用过
memset(d, -1, sizeof d);
//将起始点距离初始化为0
d[0][0] = 0;
//用数组dx和dy分别存贮x和y和偏移量
int dx[4] = { -1,0,1,0 }, dy[4] = { 0,1,0,-1 };
//只要我的队列中有元素,就说明广度搜索没搜索完
while (hh <= tt)
{
//将队头元素弹出赋值给t
//auto t其实就等于pair<int,int> t(auto 就是让系统自己猜出t的变量类型,不需要我写出冗杂的代码)
auto t = q[hh++];
//将队头弹出的点进行上下左右四次偏移
for (int i = 0; i < 4; i++)
{
//t.first即指pair这个二元组前一个元素,t.second即后一个元素
//这一步就是得到移动后x,y的坐标
int x = t.first + dx[i], y = t.second + dy[i];
//判断移动后的点是否能入队
//x >= 0 && x < n && y >= 0 && y < m首先这个点不能超出我的迷宫边界
//g[x][y] == 0 其次这个点得是我能通行的(即在这个迷宫上这个点的值为0)
//d[x][y] == -1 由于我上面有过的初始化,所以d[x][y] == -1时代表这个点第一次被搜索
//下一次搜索到这个点我就不要了,就不是最短路径了
if (x >= 0 && x < n && y >= 0 && y < m && g[x][y] == 0 && d[x][y] == -1)
{
//用d数组记录点到起始点的距离
d[x][y] = d[t.first][t.second] + 1;
//最后将bfs搜索到的点入队,进行下一次搜索
q[++tt] = { x,y };
}
}
}
//最后返回终点距离起始点的距离
return d[n - 1][m - 1];
}
int main()
{
cin >> n >> m;
//输入我的迷宫
for (int i = 0; i < n; i++)
for (int j = 0; j < m; j++)
cin >> g[i][j];
//用flag接收bfs函数返回的值
int flag = bfs();
//如果返回的值等于-1的话,说明我的bfs并没有搜索到最后的出口,即这条迷宫没有通路
//反之则有通路,并且是最短通路
if (flag!=-1) cout << flag << endl;
else cout << "此迷宫中,没有道路能走出去" << endl;
return 0;
}六、测试数据和结果
测试数据1
测试结果:

测试数据2:

测试结果:

测试数据3:

测试数据4:

测试结果: