1.问题描述

给你一个整数数组 nums，判断是否存在三元组 [nums[i], nums[j], nums[k]] 满足 i != j、i != k 且 j != k ，同时还满足 nums[i] + nums[j] + nums[k] == 0 。

请你返回所有和为 0 且不重复的三元组。

注意： 答案中不可以包含重复的三元组。

示例 1：

输入：nums = [-1,0,1,2,-1,-4]
输出：[[-1,-1,2],[-1,0,1]]
解释：
nums[0] + nums[1] + nums[2] = (-1) + 0 + 1 = 0 。
nums[1] + nums[2] + nums[4] = 0 + 1 + (-1) = 0 。
nums[0] + nums[3] + nums[4] = (-1) + 2 + (-1) = 0 。
不同的三元组是 [-1,0,1] 和 [-1,-1,2] 。
注意，输出的顺序和三元组的顺序并不重要。

示例 2：

输入：nums = [0,1,1]
输出：[]
解释：唯一可能的三元组和不为 0 。

示例 3：

输入：nums = [0,0,0]
输出：[[0,0,0]]
解释：唯一可能的三元组和为 0 。

2.难度等级

medium。

3.热门指数

★★★★☆

出题公司：阿里、腾讯、字节。

4.解题思路

方法一：暴力法

暴力法应该是我们最先想到的方法。

三层循环枚举三元组，时间复杂度很高为 $O(n^3)$。

在这之后，我们还需要使用哈希表进行去重操作，得到不包含重复三元组的最终答案，还会消耗了大量的空间。

考虑到三元组中元素的顺序可能不同，为了去重，我们可以先对三元组进行排序。如何唯一表示三元组并将其写入哈希表呢？

我们可以将三元组元素拼成一个字符串写入哈希表，然后遍历所有三元组，去掉重复的三元组。

暴力法的时间复杂度和空间复杂度都很高，因此我们要换一种思路来考虑这个问题。

方法二：排序+双指针

首先题目要求结果不包含重复三元组，而在给出的 nums 中又可能出现重复的元素。

大多数避免重复的问题，思路一般是排序。因此可以先对 nums 进行一次排序，这样做的意义一是方便使用双指针，二是遍历中也方便跳过重复项。

那么应该怎样找出三个相加为 0 的三元组呢？具体步骤如下：

1. 将数组 nums 升序排序。
2. 遍历数组，将 nums[i] 作为三元组的第一个元素。
3. 在数组剩下的数中使用双指针 j 和 k 分别指向首尾。
4. 判断 nums[i]、nums[j] 和 nums[k] 的和是否为零，如果为零，则保留下来。然后移动指针 j 和 k 直到二者相遇。

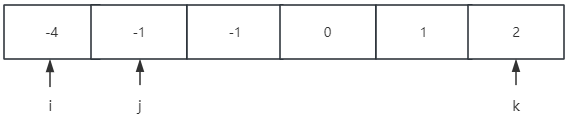
关于指针 j 和 k 的移动规则：

1.如果和为零，那么需要同时移动 j 和 k。j 往右移，k 往左移。
2.如果和小于零，那么需要提高 nums[j] 的值，所以 j 往右移，k 不动。
3.如果和大于零，那么需要减小 nums[k] 的值，所以 k 往左移，j 不动。
4.j 在左移 和 k 在右移后，与前一项可能相同，那么就需要继续移动。

关于数组的遍历规则：

1.遍历数组的次数不是整个数组的长度，只需要遍历至倒数第 3 个元素，因为是考察 3 个元素的和
2.当 nums[i] 大于 0 的时候，后面所有的三元组都不满足条件，结束遍历并返回结果。
3.当 nums[i] 与前一个数相同时，跳过本次循环。

复杂度分析：

时间复杂度：双指针移动的复杂度是 O(n)，再加上外能循环的复杂度 O(n)，所以总的时间复杂度是 $O(n^2)$。

空间复杂度：我们忽略存储答案的空间，那么空间复杂度是 O(1)。

5.实现示例

下面以 Golang 为例，给出「排序+双指针」的实现。

import (
	"golang.org/x/exp/slices"
)

func threeSum(nums []int) [][]int {
    slices.Sort(nums)
    var r [][]int
    var j, k int
    for i:=0; i < len(nums)-2; i++{
        // 跳过相同的数。
        if i > 0 && nums[i] == nums[i-1] {
            continue
        }
        // 双指针移动。
        j, k = i+1, len(nums)-1
        for j < k {
            if nums[i] + nums[j] + nums[k] == 0 {
                r = append(r, []int{nums[i], nums[j], nums[k]})
                // 同时移动左右指针。
                j++
                for j < k && nums[j] == nums[j-1] {
                    j++
                }
                k--
                for j < k && nums[k] == nums[k+1] {
                    k--
                }
            } else if nums[i] + nums[j] + nums[k] < 0 {
                // 移动左指针。
                j++
                for j < k && nums[j] == nums[j-1] {
                    j++
                }
            } else {
                // 移动右指针。
                k--
                for j < k && nums[k] == nums[k+1] {
                    k--
                }
            }
        }
    }
    return r
}

---

参考文献

15. 三数之和 - LeetCode
LeetCode题解- 题目：三数之和