本文重点

随着深度神经网络的层数的增加，神经网络会变得越来越难以训练，之所以这样就是因为存在梯度消失和梯度爆炸问题。本节课程我们将学习跳跃连接方式，它可以从某一网络层获取激活a，然后迅速反馈给另外一层，甚至是神经网络的更深层，从而解决梯度消失的问题。

传统的连接方式

这是一个两层的网络，我们来看一下它从a[l]到a[l+2]的前向传播过程是什么样的？

z[l+1] = W[l+1]a[l] + b[l+1]

a[l+1] = g(z[l+1])

z[l+2] =W[l+2]a[l+1] + b[l+2]

a[l+2] = g(z[l+2])

残差块的连接方式

上面就是传统的神经网络的前向传播的方式，而在残差块中有一点变化，我们将a[l]直接向后拷贝到神经网络的深层，在ReLU非线性激活函数前加上a[l]。a[l]的信息直接到达神经网络的深层。

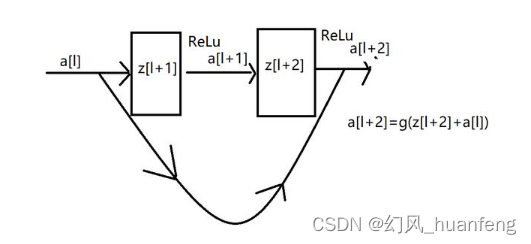
这就意味着最后这个等式(a[l+2] = g(z[l+2]))去掉了，取而代之的是另一个 R