多元线性回归（一）

news2024/12/1 0:31:07

基本概念

线性回归时机器学习中监督学习下的一种算法。回归问题主要关注是因变量（需要预测的值，可以是一个也可以是多个）和一个或多个值型的自变量（预测变量）之间的关系。
需要预测的值：即目标变量，target,y,连续值预测变量
影响目标变量的因素：X1……Xn,可以是连续值也可以是离散值。
因变量和自变量之间的关系：即模型，model，是我们要求解的。

1.1 连续值

数值型数据中，能无限细分的叫做连续型
例如身高，长度

1.2 离散型数据

不能无限细分的就叫离散型
比如序号1～20，1和2之间没有别的序号，又比如等级数据，一级二级三级是人为界定，或者我国的各省的名称，不是测量获得的。

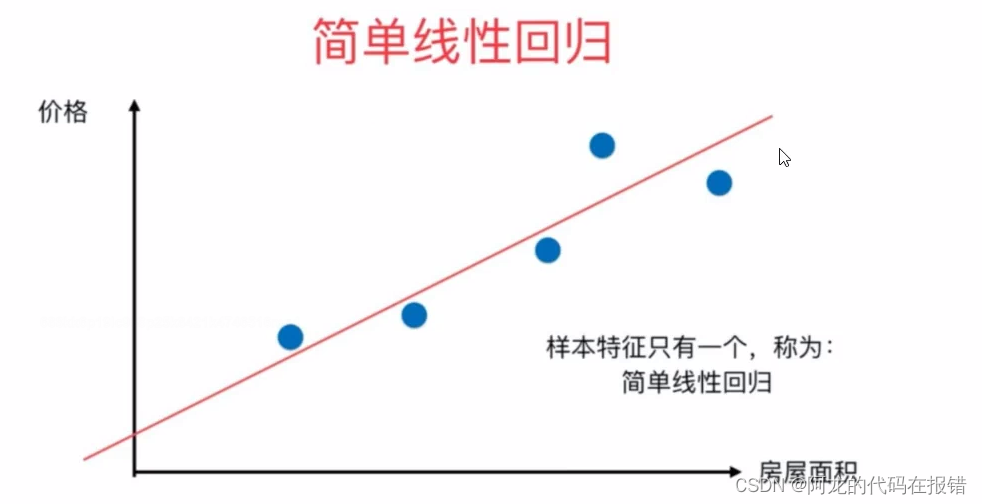
1.3 简单的线性回归

前面提到过的，算法说白的了就是公式，简单的线性回归属于一个算法，他所对应的公式
$y = w x + b$
这个公式中，y是目标变量即未来要预测的值，X是影响y的因素，w,b
是公式上的参数即要求的模型。其实b 就是截距，w就是斜率，所以和明显如果模型求出来了，未来影响y值的未知数据就是一个X值，也可以一说影响y值的因素只有哦一个，所以这就叫简单的线性回归的原因。
同时我们可以发现从x到y的计算，x只是一次方，所以这些算法叫线性回归是我原因

其实，大家在上小学的时候就已经会解一元一次方方程了，为什么那个时候哦不叫人工智能算法呢？因为人工智能算法要求的是最优解！

1.4 最优解

Actual value: 真实值，一般使用y表示
Predicted value: 预测值，是把已知的x带入到公式里面和猜出来的参数w,b计算得到的，一般使用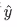在这里插入图片描述表示
Error:：误差，预测值和真实值的差距，一般使用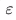表示
最优解：尽可能找到一个模型整体的误差最小，整体误差通常叫做损失Loss.
Loss:整体的误差，loss通过损失函数 loss function计算得到的
简单的线性回归的dome

1.5 多元线性回归

但是在现实生活中，往往影响y的因素不止一个，这时x就从一个变成n个了
，x1……xn 同时简单线性回归的公式就不在适用了。多元线性回归如下：

多元线性公式
在这里插入图片描述

2. 正规方程

2.1 最小二乘法

最小二乘法（Least Squares Method）是一种常见的数字优化技术，用于拟合一组数据点的最佳线性回归方程。它的目标是找到一条直线，使得该直线和数据点之间的误差平方和最小。

具体而言，最小二乘法的目标是最小化每个数据点与拟合直线之间垂直距离的平方和，即最小化所有数据点到拟合直线的残差平方和。残差是指每个数据点的实际值和集合直线在该点处的预测值之间的差异。

最小的二乘法可用于回归分析，即对一组数据拟合，并预测未来数据点的值。此外，他可以用于求解线性方程组，如先行回归模型的系数或参数估计等。

最小二乘法可以将误差转化为有确定的代数方程组（其方程式数目正好等于未知数的个数），从而可求解出这些未知参数。这个有确定解的代数方程组称为最小二乘法估计的正规方程。公式如下：

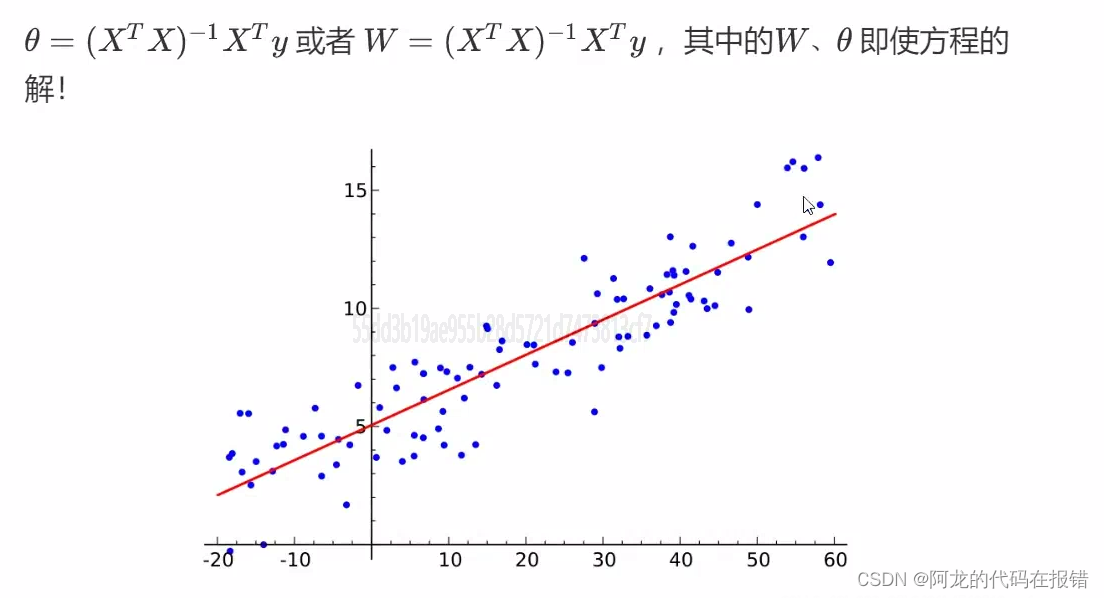
在这里插入图片描述

2.2、多元一次方程举例

1、二元一次方程

$\begin{cases} x + y=14\\ 2x - y = 10\\ \end{cases}$

2、三元一次方程

$\begin{cases} x - y + z = 100\\ 2x + y -z = 80\\ 3x - 2y + 6z = 256\\ \end{cases}$

3、八元一次方程

$\left\{\begin{aligned} & \ 14x_2 + 8x_3 + 5x_5 + -2x_6 + 9x_7 + -3x_8 = 339\\&-4x_1 + 10x_2 + 6x_3 + 4x_4 + -14x_5 + -2x_6 + -14x_7 + 8x_8 = -114\\&-1x_1 + -6x_2 + 5x_3 + -12x_4 + 3x_5 + -3x_6 + 2x_7 + -2x_8 = 30\\&5x_1 + -2x_2 + 3x_3 + 10x_4 + 5x_5 + 11x_6 + 4x_7 + -8x_8 = 126\\&-15x_1 + -15x_2 + -8x_3 + -15x_4 + 7x_5 + -4x_6 + -12x_7 + 2x_8 = -395\\&11x_1 + -10x_2 + -2x_3 + 4x_4 + 3x_5 + -9x_6 + -6x_7 + 7x_8 = -87\\&-14x_1 + 4x_3 + -3x_4 + 5x_5 + 10x_6 + 13x_7 + 7x_8 = 422\\&-3x_1 + -7x_2 + -2x_3 + -8x_4 + -6x_6 + -5x_7 + -9x_8 = -309 \end{aligned}\right.$

# 上面八元一次方程对应的X数据
X = np.array([[  0 ,14 , 8 ,  0 ,  5,  -2,   9,  -3],
 [ -4 , 10 ,  6 ,  4 ,-14 , -2 ,-14  , 8],
 [ -1 , -6  , 5 ,-12 ,  3 , -3 ,  2 , -2],
 [  5 , -2  , 3 , 10  , 5 , 11 ,  4  ,-8],
 [-15 ,-15  ,-8 ,-15 ,  7 , -4, -12 ,  2],
 [ 11 ,-10 , -2 ,  4  , 3 , -9 , -6 ,  7],
 [-14 ,  0 ,  4 , -3  , 5 , 10 , 13 ,  7],
 [ -3 , -7 , -2 , -8  , 0 , -6 , -5 , -9]])
# 对应的y
y = np.array([ 339 ,-114  , 30 , 126, -395 , -87 , 422, -309])
display(X,y)

2.3、矩阵转置公式与求导公式

转置公式如下：

$mA)^T = mA^T$ ，其中m是常数
$A + B)^T = A^T + B^T$
$AB)^T = B^TA^T$
$A^T)^T = A$

假设我们有一个矩阵 $A$ ，它是一个 $\times 2$ 的矩阵，其中包含了 $6$ 个元素。我们可以将其表示为：

$\begin{pmatrix} 1 & 2 \\ 3 & 4 \\ 5 & 6 \\ \end{pmatrix}$

现在，如果我们想要转置矩阵 $A$ ，我们可以将 $A$ 中的行和列互换。这样就得到了一个新的矩阵 $A^T$ ，它的行数和 $A$ 的列数相等，列数和 $A$ 的行数相等。在这种情况下， $A^T$ 是一个 $\times 3$ 的矩阵。我们可以使用下面的公式来计算 $A^T$ ：

$A^T_{i,j} = A_{j,i}$

也就是说，新矩阵中的第 $i$ 行和第 $j$ 列的元素等于原矩阵中的第 $j$ 行和第 $i$ 列的元素。

下面是具体的演示：

$A^T = \begin{pmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \\ \end{pmatrix}$

在上面的例子中，我们首先写出了矩阵 $A$ ，然后使用公式 $A^T_{i,j} = A_{j,i}$ 将其转置为矩阵 $A^T$ 。转置矩阵的行和列与原矩阵相反，其中原矩阵的第 $i$ 行变为了新矩阵的第 $i$ 列，原矩阵的第 $j$ 列变为了新矩阵的第 $j$ 行。

求导公式如下：

$ $\frac{\partial X^T}{\partial X} = I$ 求解出来是单位矩阵
$\frac{\partial X^TA}{\partial X} = A$
$ $\frac{\partial AX^T}{\partial X} = A$
$\frac{\partial AX}{\partial X} = A^T$
$\frac{\partial XA}{\partial X} = A^T$
$\frac{\partial X^TAX}{\partial X} = (A + A^T)X;$ A不是对称矩阵
$\frac{\partial X^TAX}{\partial X} = 2AX;$ A是对称矩阵

2.4、推导正规方程 $\theta$ 的解

矩阵乘法公式展开

$J(\theta) = \frac{1}{2}(X\theta - y)^T(X\theta - y)$
$J(\theta) = \frac{1}{2}(\theta^TX^T - y^T)(X\theta - y)$
$J(\theta) = \frac{1}{2}(\theta^TX^TX\theta - \theta^TX^Ty -y^TX\theta + y^Ty)$

进行求导（注意X、y是已知量， $\theta$ 是未知数）：

$J'(\theta) = \frac{1}{2}(\theta^TX^TX\theta - \theta^TX^Ty -y^TX\theta + y^Ty)'$

$y^Ty$ 是常量
$J'(\theta) = \frac{1}{2}((\theta^TX^TX\theta)' - (\theta^TX^Ty)' -(y^TX\theta)')$