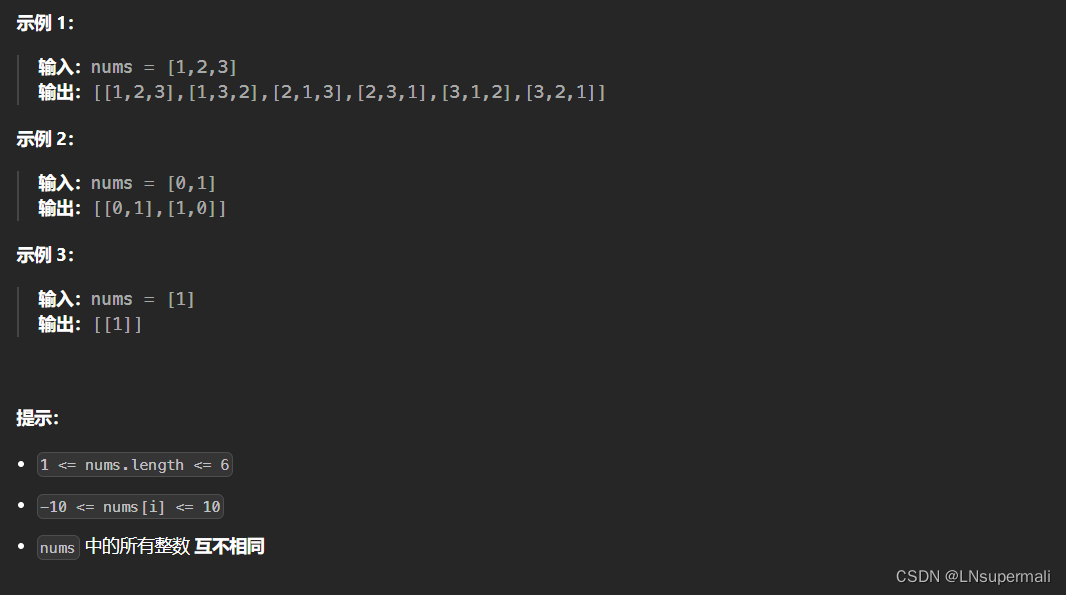
Problem: 46. 全排列

题目描述

给定一个不含重复数字的数组 nums ，返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。

思路

1.该题目要求求出一个数组的全排列，我们可以利用回溯模拟出一个对数组中所有元素排列的穷举。
2.对于回溯，关键是要找出回溯过程中的可选列表，决策阶段和路径，对于本题目：

2.1我们定义一个一维数组path用于在回溯过程中记录回溯的路径
2.2可选列表为所给定的数组nums中除去路径path中的数据

解题方法

1.定义一个二维数组result(全局变量)记录最终的全排列；
2.定义一维数组path用于记录回溯过程中的决策路径，并编写回溯函数

2.1回溯函数的退出条件为：决策阶段等于数组nums的长度（由于本题目是要求取一个数组中元素的全排列，所以退出条件如此）当等于时我们将当前路径添加到结果集合（由于路径path在递归回溯的过程中一直会修改，所以我们直接再新创建一个ArrayList集合并将path中的内容拷贝进去再一并添加到结果集合）
2.2 利用for循环，并判断若当前路径path中不存在nums中的元素则将其添加到path中，并开始递归，若存在则不处理，
2.3 在回溯的过程中，我们需要删除当前路径中的最后一个值。

复杂度

时间复杂度:

$O(n\times n!)$

空间复杂度:

$O(n)$

Code

class Solution {
    //Result list
    private List<List<Integer>> result = new ArrayList<>();

    /**
     * Get full permutation
     * @param nums An array to be arranged
     * @return List<List<Integer>>
     */
    public List<List<Integer>> permute(int[] nums) {
        //Path
        List<Integer> path = new ArrayList<>();
        backtracking(nums,0,path);
        return result;
    }

    /**
     * Full permutation is obtained by backtracking algorithm
     * @param nums Optional list(nums removes data that exists in path)
     * @param k Decision stage
     * @param path Recode the current decision
     */
    private void backtracking(int[] nums, int k, List<Integer> path) {
        //End condition
        if (k == nums.length) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = 0; i < nums.length; ++i) {
            if (path.contains(nums[i])) {
                continue;
            }
            //Chose
            path.add(nums[i]);
            //Recursion
            backtracking(nums, k + 1, path);
            //Undo selection
            path.remove(path.size() - 1);
        }
    }
}