题目1:583 两个字符串的删除操作
题目链接:两个字符串的删除操作
对题目的理解
返回使两个单词word1和word2相同的最少删除多少个元素,两个单词至少包含一个字母,且仅包含小写字母
思路1:这道题与昨天的不同子序列很相似,只是有一点不同,不同子序列是使用s字符串去匹配t字符串,而本题可以对word1进行删减得到word2,也可以用word2删减获得word1,经过一系列删除操作,最终两个单词相等就可以了。
思路2:本题其实就是求word1和word2达到最长公共子序列时,使用两个单词的长度之和减去最长公共子序列的长度的2倍。
动态规划(思路1)
动规五部曲
1)dp数组及下标i的含义
dp[i][j]:以i-1结尾的word1和以j-1结尾的word2达到word1和word2相同的最少操作次数
2)递推公式
还是考虑两种情况,当前子串word1结尾的字符与子串word2结尾的字符相等和不等的情况
i)结尾的字符相等,即word1[i-1]==word2[j-1],因为已经相等了,这两个字符就不会改变操作的次数,那么此时就不用考虑这两个字符了,(模拟将这两个字符删除),则当前的结果与这两个字符的前面的字符结尾(word1[i-1],word2[j-1])的结果相同,即dp[i][j] = dp[i-1][j-1]
ii)结尾的字符不等,因为word1[i-1]和word2[j-1]两个字符不等,所以考虑删除元素,这又可以分为3种情况,
删除word1[i-1] ,也就是不考虑word1[i-1]这个元素了,那么在word1中没有这个元素了,则最终的结果应该是其前一个字符word1[i-2]与word2[j-1]进行比较,看是否相等,
即 dp[i][j]=dp[i-1][j]+1,因为删除一个元素,所以加1
删除word2[j-1] ,不考虑word2[j-1]这个元素了,那么在word2中就没有这个元素了,则最终的结果应该是word2子串的前一个字符word2[j-2]与word1[i-1]进行比较,看是否相等,
即dp[i][j]=dp[i][j-1],因为删除了一个元素,所以加1
删除word1[i-1]和word2[j-1],不考虑word1[i-1]和word2[j-1]这两个元素了,那么在word1和word2中就没有这两个元素了,最终就是word2子串的前一个字符word2[i-2]与word1子串的前一个字符word1[i-2]进行比较 ,即 dp[i][j]=dp[i-1][j-1]+2,因为删除了2个元素,所以加2
dp[i][j] = min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+2)
3)dp数组初始化

根据递推公式,第一行,第一列都要进行初始化,即dp[i][0] dp[0][j]都需要进行初始化
根据dp数组定义 dp[i][0]代表以i-1结尾的word1和以-1结尾的word2相同的最小操作次数,word2以-1结尾,说明word2是空串,那么要想达到两个子串相等,说明word1需要删除i个元素,需要最少操作i次,所以dp[i][0]=i
同理,dp[0][j]代表以-1结尾的word1和以j-1结尾的word2相同的最小操作次数,word1是空串,此时要想让两个子串相等,word1也需要变为空串,需要将word2中的元素全部删除才可以,即删除j个元素,最少操作j次 ,所以dp[0][j]=j
4)遍历顺序
根据递推公式,从左到右遍历,从上到下遍历
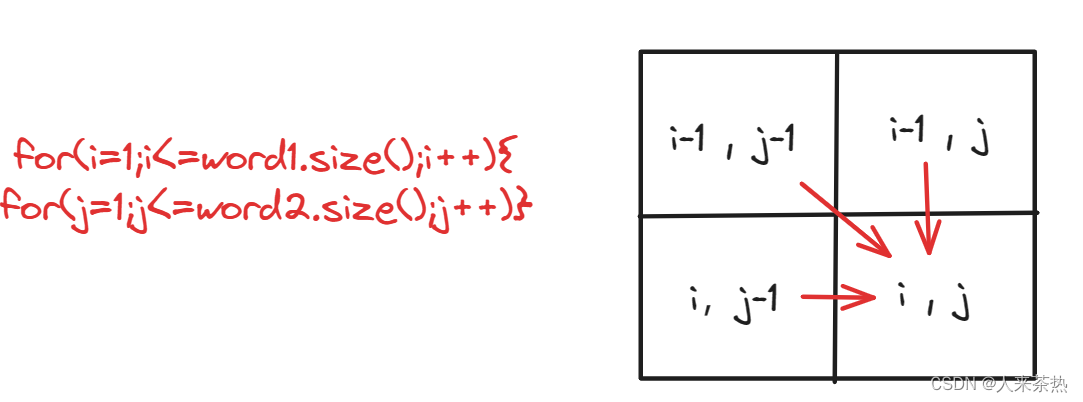
5)打印dp数组
代码,注意定义dp数组的时候,一定要word1.size()+1,一定要加1,因为dp数组的定义是以i-1结尾,最终要遍历到最后一个元素word1.size()-1的时候,才是dp数组的最后一个元素word1.size()减去1为结尾
class Solution {
public:
int minDistance(string word1, string word2) {
//定义dp数组
vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1));
//初始化dp数组
for(int i=0;i<word1.size();i++) dp[i][0]=i;
for(int j=0;j<word2.size();j++) dp[0][j]=j;
for(int i=1;i<=word1.size();i++){
for(int j=1;j<=word2.size();j++){
if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];
else dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));
}
}
return dp[word1.size()][word2.size()];
}
};上面的代码会出现如下错误

根据出现的错误,将其对应的各个dp数组打印出来,发现dp[0][1]以及dp[1][0]仍是0,并没有初始化成1,所以初始化这里出现了问题

就是因为在初始化的时候,没有将dp[word1.size()][0]和dp[0][word2.size()]初始化
注意初始化数组时,因为是初始化整个dp[i][j],所以将dp[i][0]和dp[0][j]整个进行初始化,所以,i从0到word1.size()都要初始化 ,j从0到word2.size()都要初始化,注意初始化时,一定要使得i<=word1.size(),j<=word2.size(),等号不能丢掉,否则就会在案例出现的时候出现错误
因此,将代码修改如下:
class Solution {
public:
int minDistance(string word1, string word2) {
//定义dp数组
vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1));
//初始化dp数组
for(int i=0;i<=word1.size();i++) dp[i][0]=i;
for(int j=0;j<=word2.size();j++) dp[0][j]=j;
for(int i=1;i<=word1.size();i++){
for(int j=1;j<=word2.size();j++){
if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];
else dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+2));
}
}
return dp[word1.size()][word2.size()];
}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
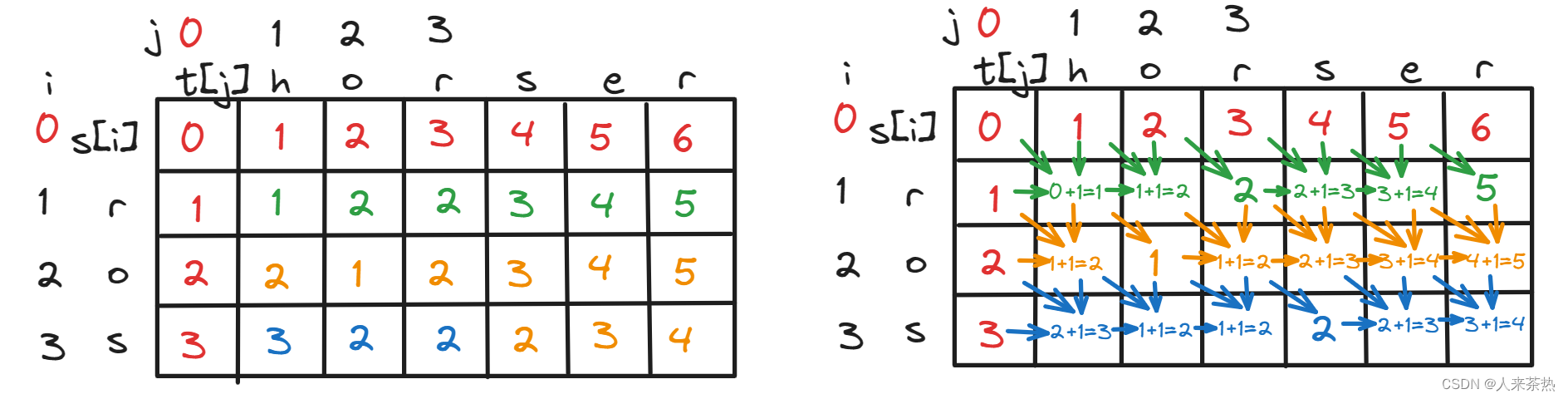
流程图
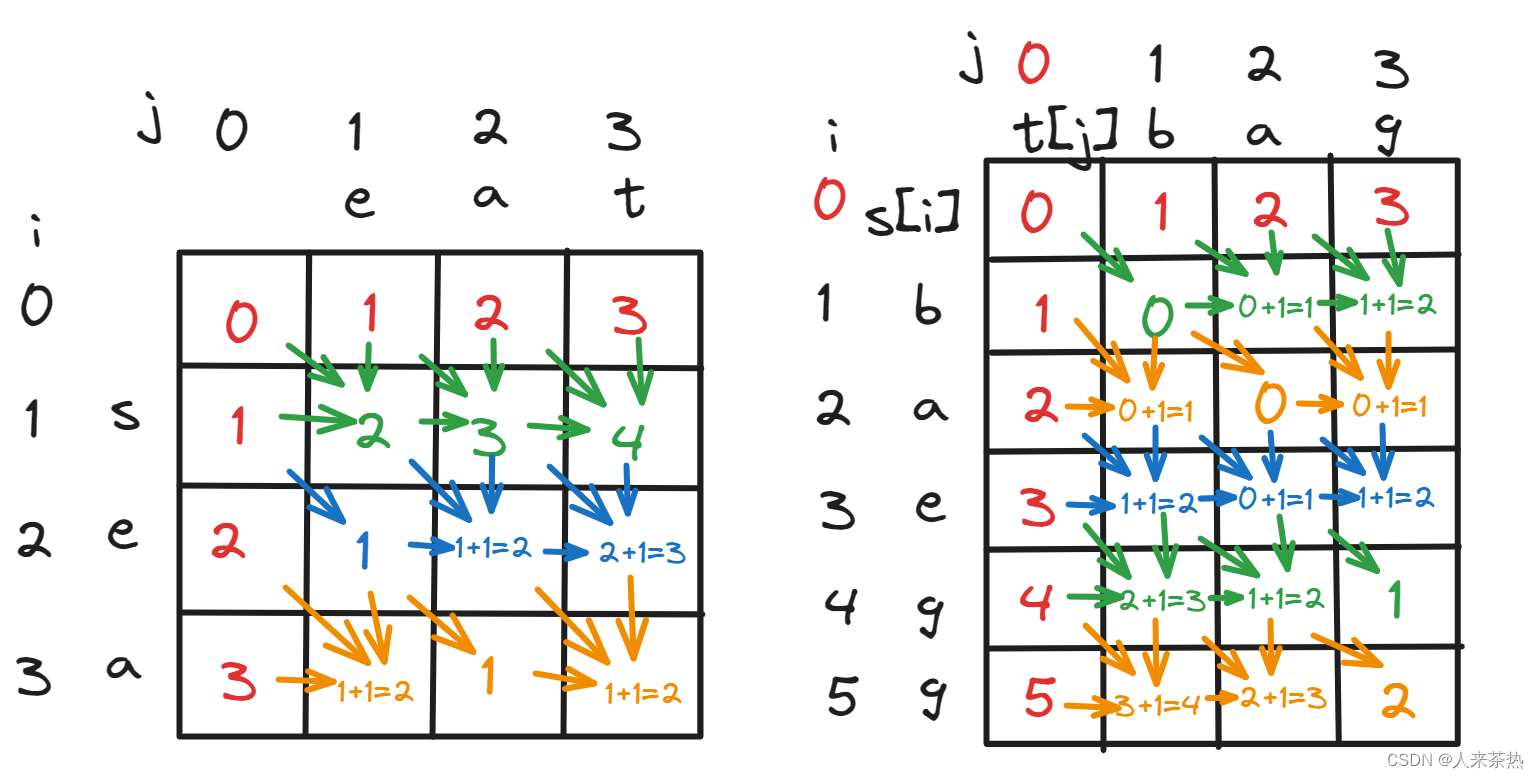
动态规划(思路2)
思路2:本题也可以在求最长公共子序列的基础上进行求解,将word1和word2的最长公共子序列的长度求出来,然后使用word1和word2的长度之和减去2倍的公共子序列的长度,即为所求。
流程
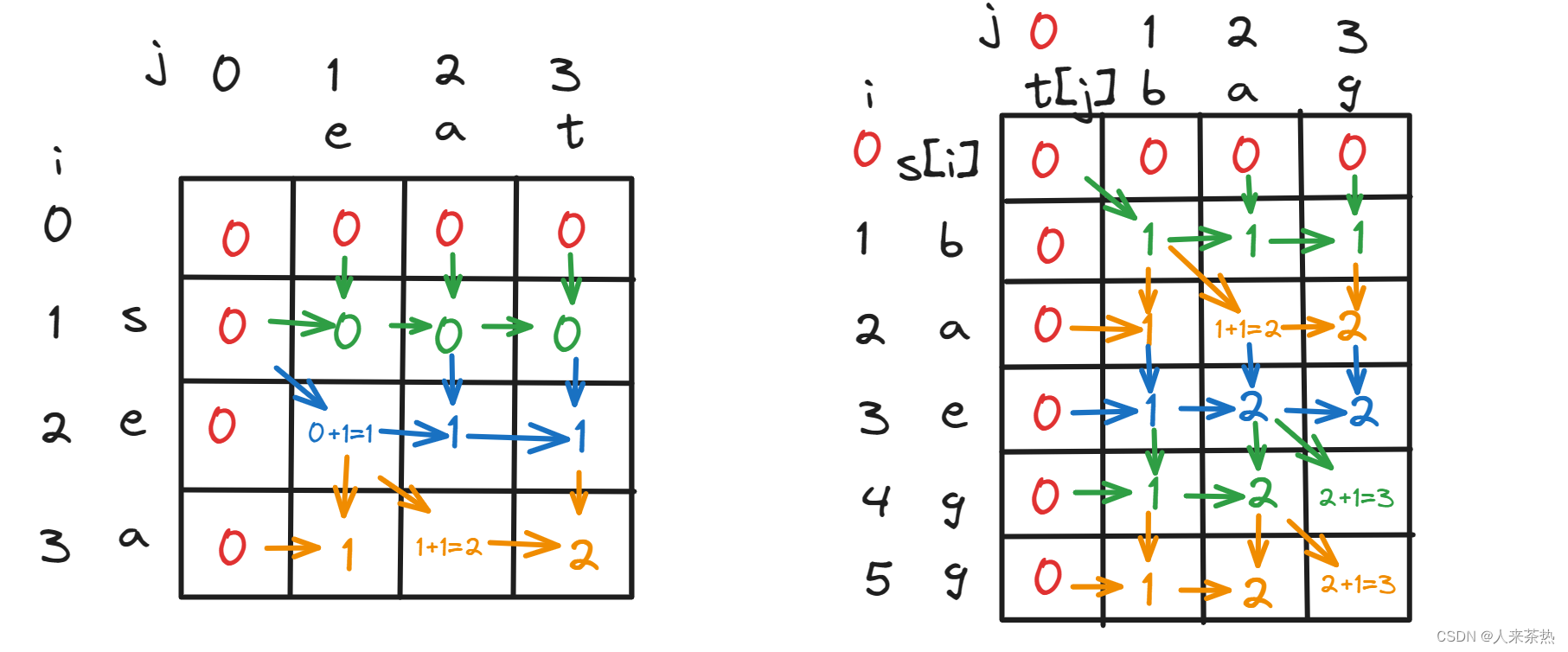
代码
class Solution {
public:
int minDistance(string word1, string word2) {
//定义并初始化dp数组
vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1,0));
for(int i=1;i<=word1.size();i++){
for(int j=1;j<=word2.size();j++){
if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1]+1;
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);
}
}
int result = word1.size()+word2.size()-2*dp[word1.size()][word2.size()];
return result;
}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
题目2:72 编辑距离
题目链接:编辑距离
对题目的理解
返回将单词word1转换成word2使用最少的操作数,两个单词的长度大于等于0,且均由小写字母组成,操作包括插入一个字符,删除一个字符以及替换一个字符
动态规划
动规五部曲
1)dp数组及下标i的定义
dp[i][j]:以下标i-1结尾的word1和以下标j-1结尾的word2相同的最少操作次数
2)递推公式
还是分为两种情况,两个元素相等以及两个元素不等的情况
1)两个元素word1[i-1]和word2[j-1]相等,则不考虑这两个元素,因为已经相等了,所以不需要对二者进行操作,只需要考虑前面的word1[i-2]和word2[j-2]就行,dp[i][j]=dp[i-1][j-1]
2)两个元素word1[i-1]和word2[j-1]不相等,则需要对元素进行删减以及替换的操作,所以这又可以分为3种情况
i)只考虑word1[i-1],只对这个元素进行操作,当word1[i-1]不等于word2[j-1]时,将word1[i-1]删除,那么此时对于word1而言,就是以word1[i-2]为结尾的子串与word2[j-1]为结尾的子串的最小操作次数的基础上进行操作(删除)加1,因此,dp[i][j]=dp[i-1][j]+1 加1是因为进行了一个删除操作
ii)只考虑word2[j-1],只对这个元素进行操作,当word1[i-1]不等于word2[j-1]时,将word2[j-1]删除,那么对于word2而言,只剩下以word2[j-2]为结尾的子串与word1[i-1]为结尾的子串的最小操作次数的基础上进行操作(删除)加1,dp[i][j]=dp[i][j-1]+1 加1是因为进行了一个删除操作
注:word2添加一个元素,相当于word1删除一个元素,例如 word1 = "ad" ,word2 = "a",word1删除元素'd' 和 word2添加一个元素'd',变成word1="a", word2="ad", 最终的操作数是一样!
iii)如果word1[i-1]不等于word2[j-1],要使得这两个位置对应的元素相等(dp[i][j]=dp[i-1][j-1],这个等式是word[i-1]和word[j-1]相等的情况,但是此时是要让这两个元素相等,所以需要考虑这两个元素在原来以word1[i-2]为结尾的子串和以word2[j-2]为结尾的子串相同进行操作的基础上加上一个替换的操作就ok),只需要dp[i][j]=dp[i-1][j-1]+1 加1是因为进行了一次替换操作
dp[i][j]= min(dp[i-1][j]+1,dp[i][j-1]+1,dp[i-1][j-1]+1)
3)dp数组初始化
根据递推公式,第一行和第一列需要初始化,
根据dp数组的定义,dp[i][0]表示以下标i-1为结尾的word1和以下标-1为结尾的word2相同的最少操作次数,而以下标-1为结尾的word2是一个空串,要想使得这两个串的长度相等,那么word1至少需要操作i次,因为word1中含有i个元素
dp[0][j]表示以下标-1为结尾的word1和以下标j-1为结尾的word2相同的最少操作次数,而以下标01结尾的word1是一个空串,要想使得word1和word2的长度相等,那么word2至少需要操作j次,因为word2中含有j个元素
因此初始化如下
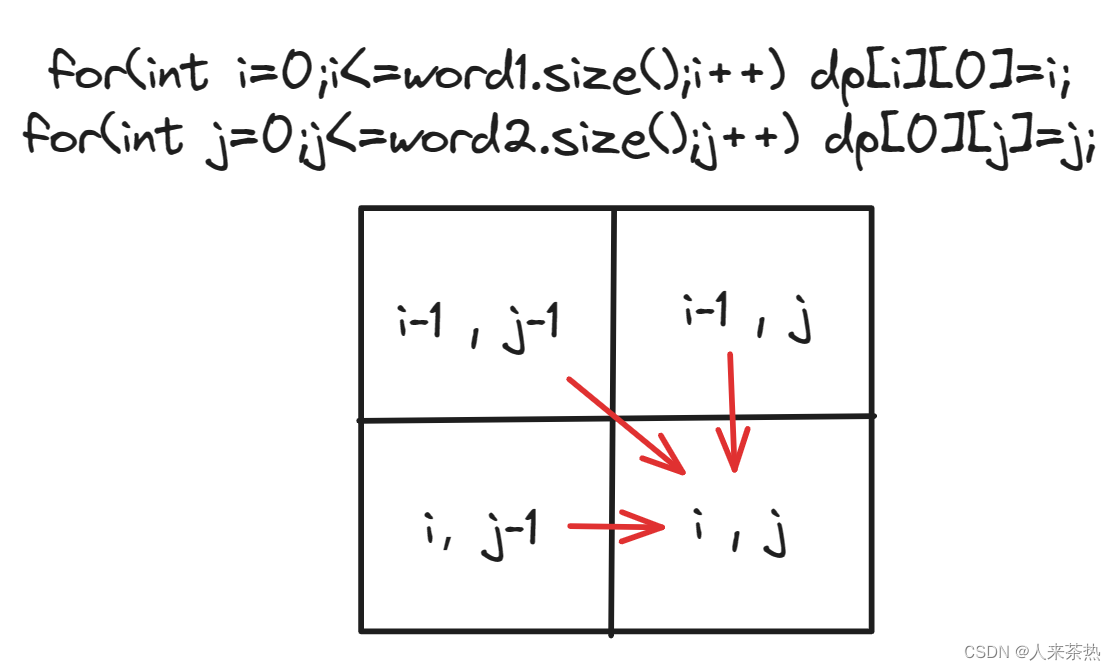
注意for循环中一定要是小于等于,一定要有等于,这样才能确保dp数组中的最后一个边界值,即dp[word1.size()][0]和dp[0][word2.size()]初始化了,如果只写小于的话,这组元素就会被落掉,相当于dp[word1.size()][0]和dp[0][word2.size()]没有进行初始化,默认为0
4)遍历顺序
根据递推公式,从左往右遍历,从上到下遍历
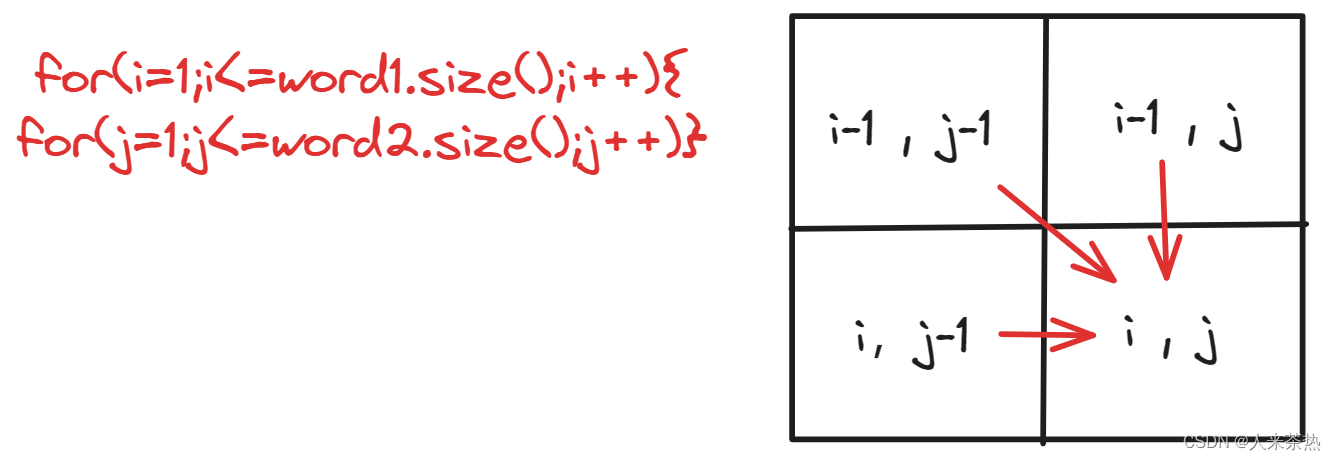
5)打印dp数组
最终的结果在dp[word1.size()][word2.size()]中
代码
class Solution {
public:
int minDistance(string word1, string word2) {
//定义dp数组
vector<vector<int>> dp(word1.size()+1,vector<int>(word2.size()+1));
//初始化dp数组
for(int i=0;i<=word1.size();i++) dp[i][0]=i;
for(int j=0;j<=word2.size();j++) dp[0][j]=j;
for(int i=1;i<=word1.size();i++){
for(int j=1;j<=word2.size();j++){
if(word1[i-1]==word2[j-1]) dp[i][j]=dp[i-1][j-1];
else dp[i][j]=min(dp[i-1][j]+1,min(dp[i][j-1]+1,dp[i-1][j-1]+1));
}
}
return dp[word1.size()][word2.size()];
}
};- 时间复杂度: O(n * m)
- 空间复杂度: O(n * m)
代码流程
删减元素
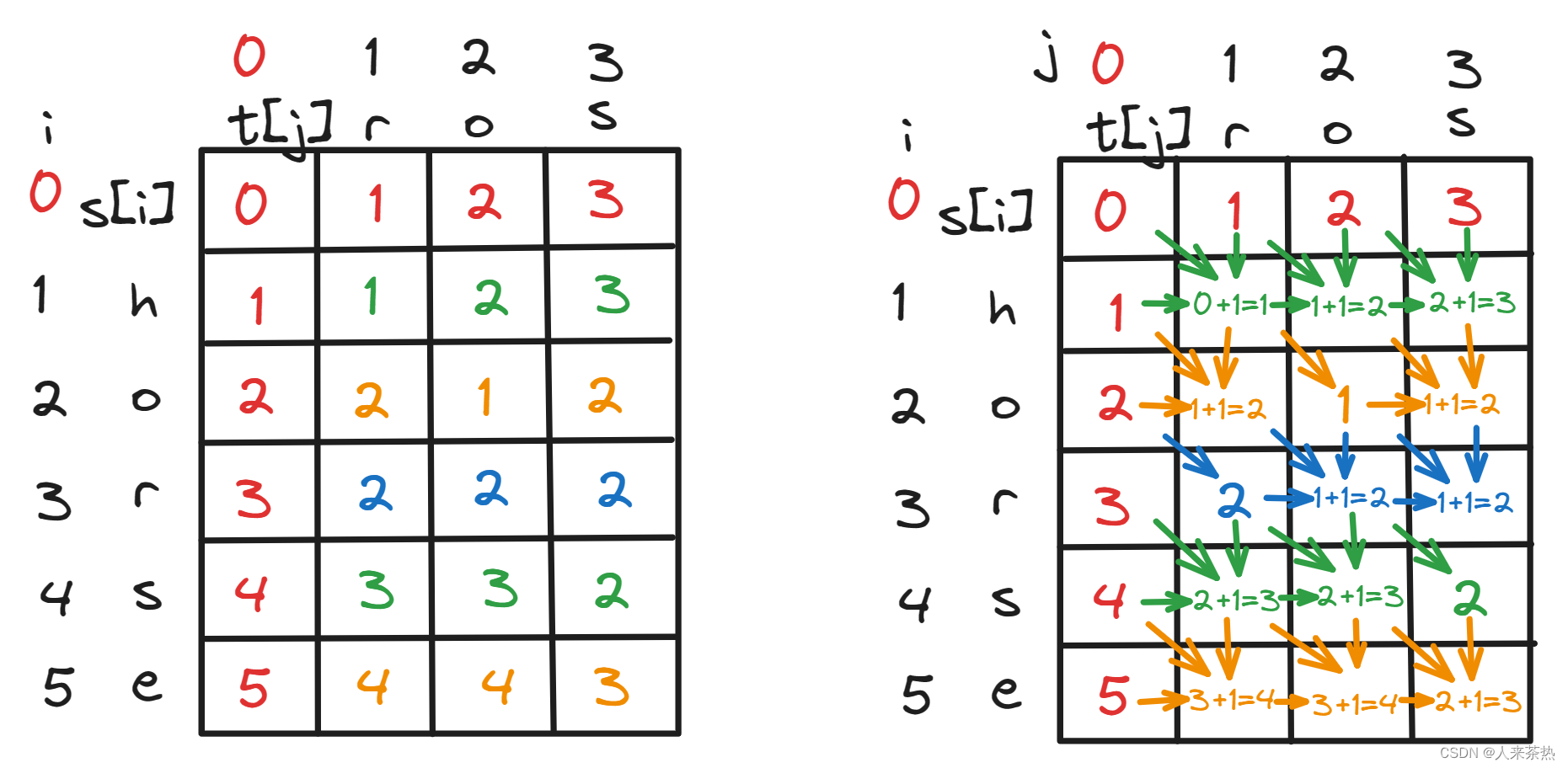
添加元素