目录
- 一、树和二叉树的概念
- (一)二叉树的定义和性质
- (二)树和二叉树的区别
- 二、完全二叉树和满二叉树
- 三、二叉树的遍历
- (一)由序列确定二叉树
- (二)不同遍历序列的关系
- 四、二叉树的性质
- (一)二叉树结点度的关系
- (三)二叉树的最小与最大深度(高度)
- 五、线索二叉树
- 六、哈夫曼树
- (一)哈夫曼树的定义
- (二)哈夫曼树的构建步骤
- (三)哈夫曼编码
一、树和二叉树的概念
(一)二叉树的定义和性质
1、简要说明二叉树的概念。二叉树有哪些性质。(至少写出3个)
答:二叉树是一种树形结构,每个结点至多只有两棵子树,即二叉树中不存在度大于2的结点,且二叉树的子树也有左右之分。
性质:
①非空二叉树的叶子结点等于度为2的结点数加1,即n0=n2+1;
②高度为h的二叉树至多有2h-1个结点;
③一棵树高为h的完全二叉树至少有2h-1个结点,至多有2h-1个结点,
④一棵树高为h的完全二叉树中,总结点数N与高h的关系是h=⌈log2(n+1)⌉;
⑤对于一棵含有n个结点的二叉树,当它为完全二叉树时,具有最小高度,最小高度为h=⌈log2(n+1)⌉或⌊log2n⌋+1;当它为一棵单支树时具有最大高度,为一个线性表,即最大高度为n。
(二)树和二叉树的区别
1、树和二叉树的区别是什么?
答:树和二叉树均有且只有一个根结点,根结点没有前驱结点,除了根结点其他所有结点都只有一个前驱结点,剩下的结点为m(m≥0)个互不相交的非空集合。树中结点的后继结点可以是任意多个,而二叉树中结点的后继结点最多只能有两个,即二叉树的度小于等于2。
二、完全二叉树和满二叉树
1、什么是完全二叉树?什么是满二叉树?它们两者之间的关系是怎么样的?
答:深度(高度)为h,具有2h-1个结点的二叉树,其中每层结点都是满的二叉树,称为满二叉树,而若一棵树中除最后一层外,其余层的结点都是满的或结点的右子树缺少连续的若干个结点 ,则称为完全二叉树。满二叉树是完全二叉树的特例,可以说,若一棵树是满二叉树,则它必是完全二叉树,但不能说一个完全二叉树必是满二叉树。
三、二叉树的遍历
(一)由序列确定二叉树
1、由二叉树先序遍历和后序遍历序列能否唯一确定一棵二叉树?请举例解释。
答:不能。例如,下面两个二叉树的前序序列和后序序列均相同,但是不是相同的二叉树。
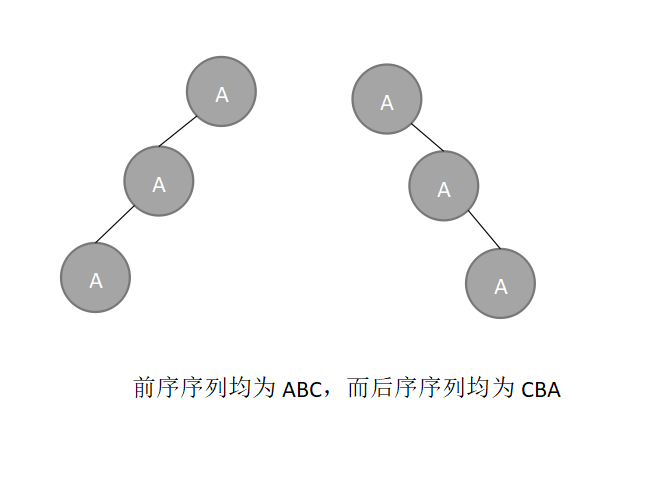
(二)不同遍历序列的关系
1、试分析非空二叉树在什么情况下,其前序遍历序列与后序遍历序列相同以及前序遍历序列与后序遍历序列相反?
答:若一棵二叉树为空树或只有根结点,则其前序遍历序列和后序遍历序列相同。若一棵非空的二叉树只有一个叶子结点或二叉树的高度等于结点个数,则其前序遍历序列和后序遍历序列相反。
四、二叉树的性质
(一)二叉树结点度的关系
1、证明任意一棵二叉树中,若叶子结点的个数为n0,度为2的结点个数为n2,则必用n0=n2+1。
答:设二叉树中度为1的结点个数为n1,由于二叉树中所有结点的度均小于等于2,所以总结点个数为N=n0+n1+n2,另外,二叉树中除了根结点外,其他结点至少有一个分支,度为1的结点有一个分支,度为2的结点有两个分支,则分支总数=N-1=n1+2n2,联立两式,可得n0=n2+1。
(三)二叉树的最小与最大深度(高度)
1、具有n个结点的二叉树,什么时候下其深度达到最大?什么情况下其深度达到最小?
答:单支树时,二叉树的深度最大,最大为n层;若深度为h,结点个数满足2h+1-1时,即为满二叉树时,二叉树的深度最小。
五、线索二叉树
1、线索二叉树的作用是什么?
答:由于在含有n个结点的二叉树中,有n+1个空指针。对于叶子结点,它有两个空指针,对于度为1的结点,只有一个空指针。将这些空指针利用起来,让其存放指向该结点的前驱或后继,从而使遍历二叉树更加简便,加快查找结点的前驱或后继的速度。
六、哈夫曼树
(一)哈夫曼树的定义
1、什么是哈夫曼树?若哈夫曼树有n个叶子结点,则其结点总数是多少?
答:哈夫曼树是一棵最优二叉树,给定n个带有权值的叶子结点,构造一棵二叉树,使构造的二叉树的带权路径长度最小,即为最优二叉树,也称为哈夫曼树。若哈夫曼树有n个叶子结点,由于哈夫曼树中只有度为0和2的结点,不存在度为1的结点,则其结点总数为N=2n-1。
(二)哈夫曼树的构建步骤
1、写出构建哈夫曼树的哈夫曼算法思想。
答:基于给定的n个带权值的结点构成的初始森林,首先,选出两棵权值最小的树作为左右子树相加,得出的权值之和是一个新根结点的权值,然后,将新结点插入到森林中,同时将左右子树从森林中删除,重复选取,直到森林中只有一棵树时,即为哈夫曼树。
(三)哈夫曼编码
1、哈夫曼编码是什么?
答:哈夫曼编码是一种可变长度编码,且是无前缀编码,它根据字符出现的概率来对每个字符设定二进制编码,规定一个编码不能是其它编码的前缀,主要应用在数据压缩、加密解密等场景。