目录
647. 回文子串
516.最长回文子序列
动态规划总结篇
647. 回文子串
题目链接:647. 回文子串
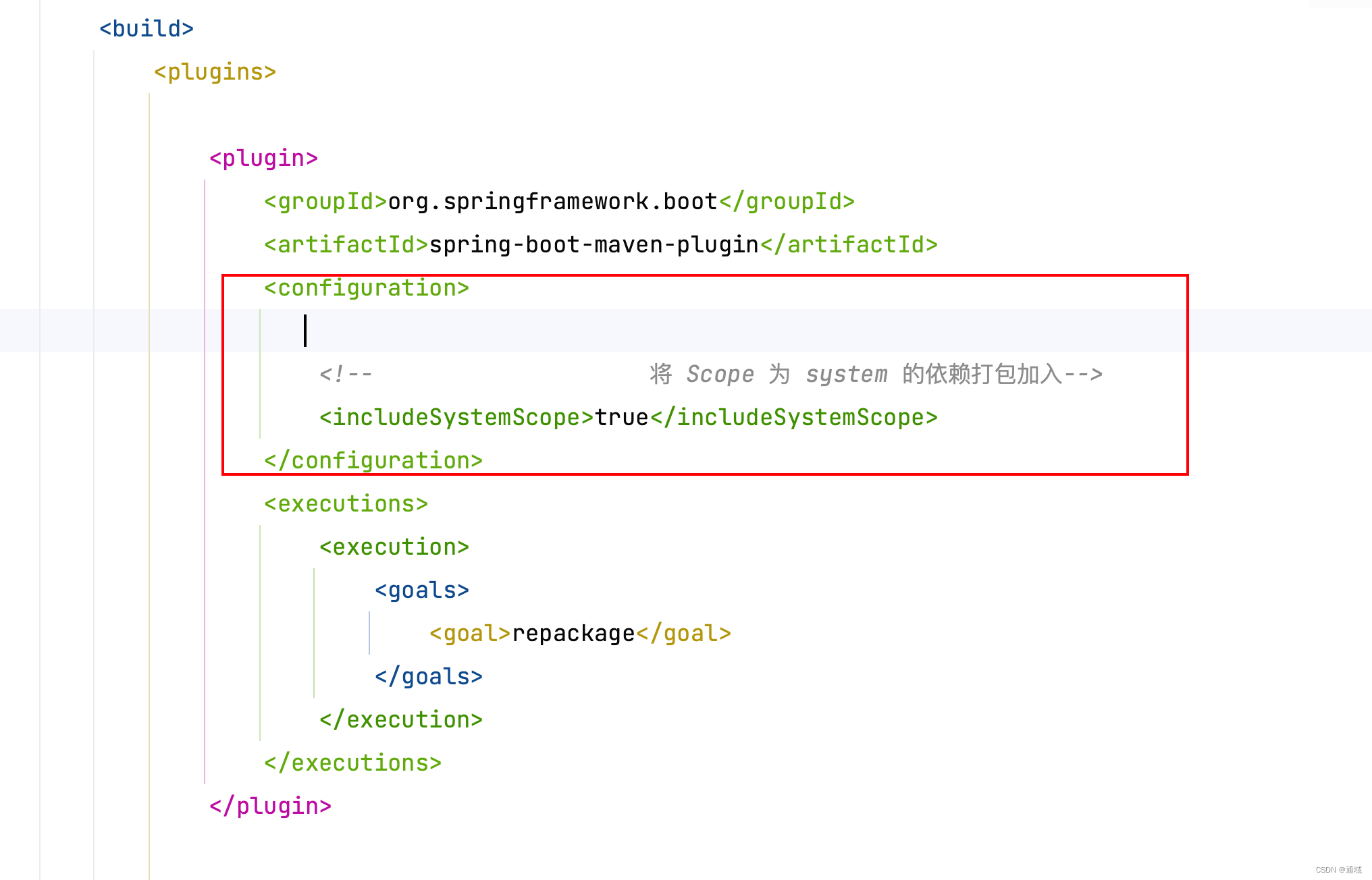
(1)dp[ i ][ j ] 表示从 i 到 j 的字符串是否为回文子串;
(2)若 s[ i ] == s[ j ]
若 j - i <= 1 dp[ i ][ j ] = true;
else dp[ i ][ j ] = dp[ i + 1 ][ j - 1 ];
else
dp[ i ][ j ] = false;
(3)dp[ i ][ j ] = false;
(4)i 从大到小,j 从 i 到大
class Solution {
public:
int countSubstrings(string s) {
int ans = 0;
vector<vector<bool>> dp(s.size(), vector<bool>(s.size(), false));
for(int i = s.size() - 1; i >= 0; --i){
for(int j = i; j < s.size(); ++j){
if(s[i] == s[j] && (j - i <= 1 || dp[i+1][j-1])){
dp[i][j] = true;
++ans;
}
}
}
return ans;
}
};516.最长回文子序列
题目链接:516. 最长回文子序列
(1)dp[ i ][ j ] 表示以 i 为开头、j 为结尾的字符串的最长回文子序列;
(2)if( s[ i ] == s[ j ] ) dp[ i ][ j ] = dp[ i + 1 ][ j - 1 ] + 2;
else dp[ i ][ j ] = max( dp[ i + 1 ][ j ], dp[ i ][ j - 1 ] );
(3)寻找 dp 的前一状态时,i 不断 +1,j 不断 -1,i 最大不超过 j,j 最小不超过 i,所以需要初始化 i == j 的情况,dp[ i ][ i ] = 1;
(4)i 从大到小,j 从 i 到大
class Solution {
public:
int longestPalindromeSubseq(string s) {
vector<vector<int>> dp(s.size(), vector<int>(s.size(), 0));
for(int i = 0; i < s.size(); ++i) dp[i][i] = 1;
for(int i = s.size() - 1; i >= 0; --i){
for(int j = i + 1; j < s.size(); ++j){
if(s[i] == s[j]) dp[i][j] = dp[i + 1][j - 1] + 2;
else dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
}
}
return dp[0][s.size() - 1];
}
};动态规划总结篇
动态规划题型:
- 背包问题
- 打家劫舍
- 股票问题
- 子序列问题
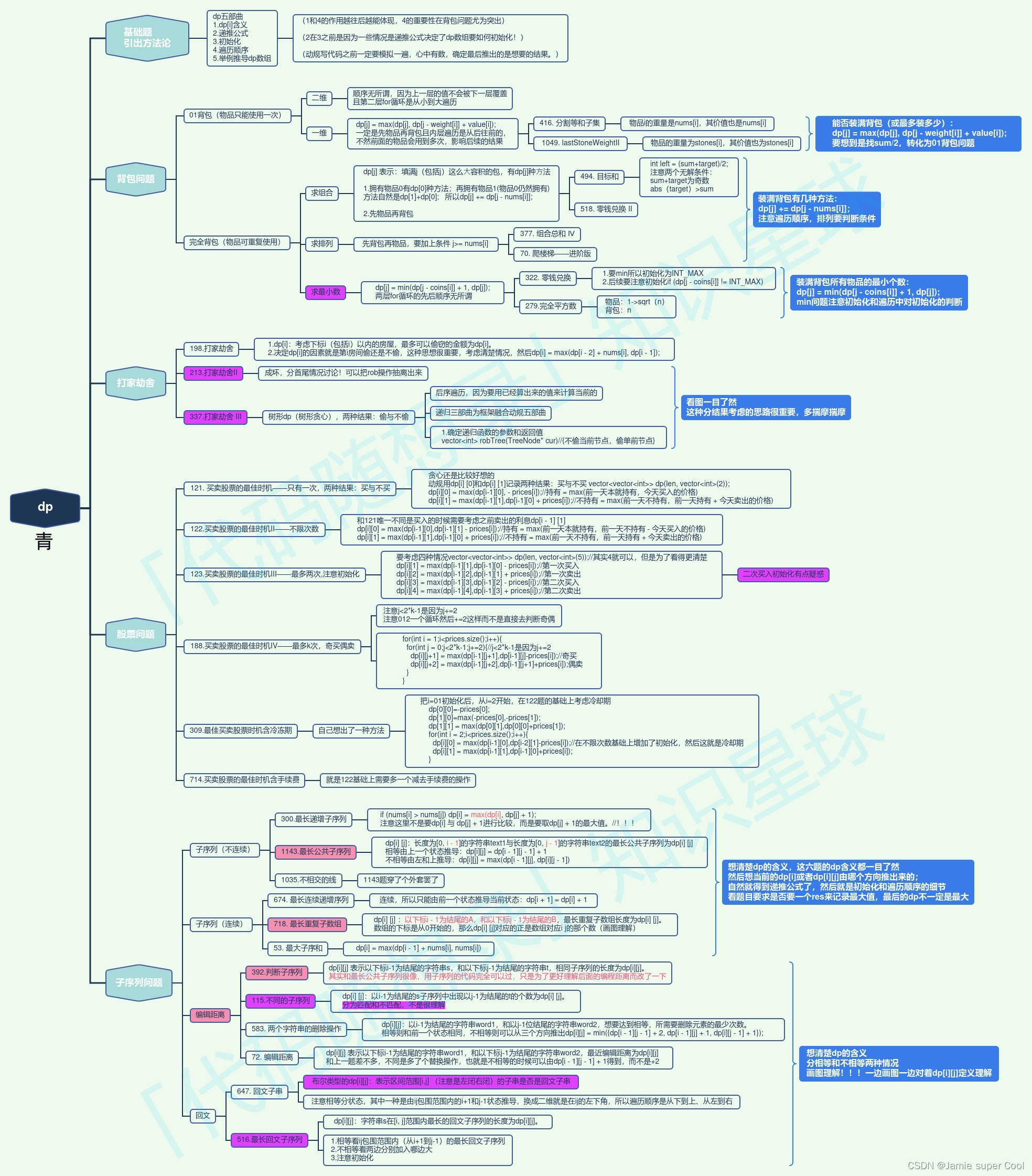
上图来自 代码随想录知识星球 成员:青