文章目录
- 一、定义
- 1、任务
- 2、构造
- 3、输出形式
- 二、(有穷状态)自动机
- 三、正则文法和状态图
- 四、词法分析程序流程
- 1、单词及内部表示
- 2、词法分析程序需要引用的公共(全局)变量和过程
- 五、自动机
- 1、DFA(确定的有穷状态自动机)
- 2、NFA(不确定的有穷自动机)
- 正则表达式
- 3、NFA确定化
- 1)一些概念
- 2)确定化过程
- 4、DFA的极简化(极小化)
- 1)一些概念
- 2)矩阵法
- 3)分割法
- 六、词法分析的自动化
一、定义
1、任务
依据文法(词法)分析和识别单词。
2、构造
源程序是由字符序列构成的,词法分析扫描源程序(字符串),根据语言的词法规则分析并识别单词,并以某种编码形式输出。
单词:是语言的基本语法单位,一般语言有四大类单词
<1>语言定义的关键字或保留字(如BEGIN、END、IF)
<2>标识符:由用户定义,表示各种名字的字符串
<3>常数:无符号数、布尔常数、字符串常数等
<4>分界符(运算符) (如
+
、
−
、
∗
、
/
、
;
、(、)
…
…
+、-、*、/、;、(、) ……
+、−、∗、/、;、(、)……)
3、输出形式
按单词种类分类
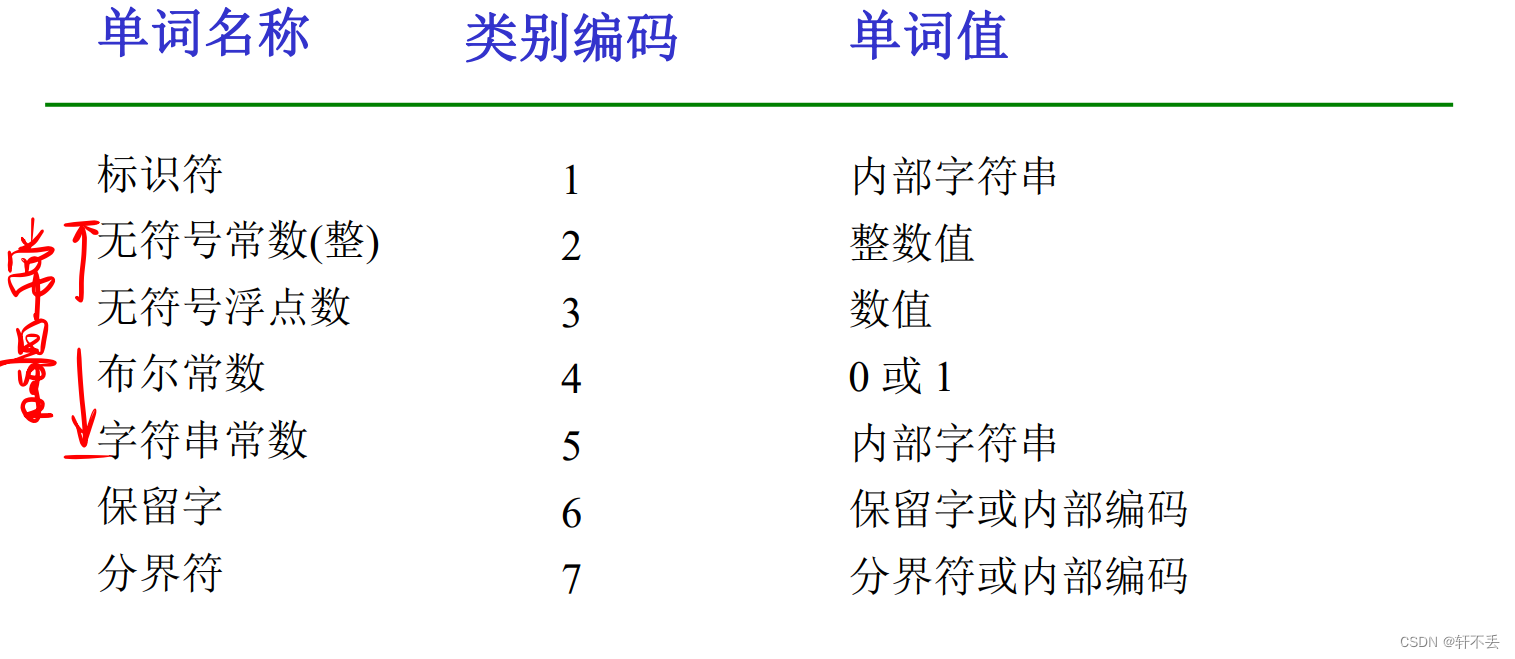
保留字和分界符采用一符一类
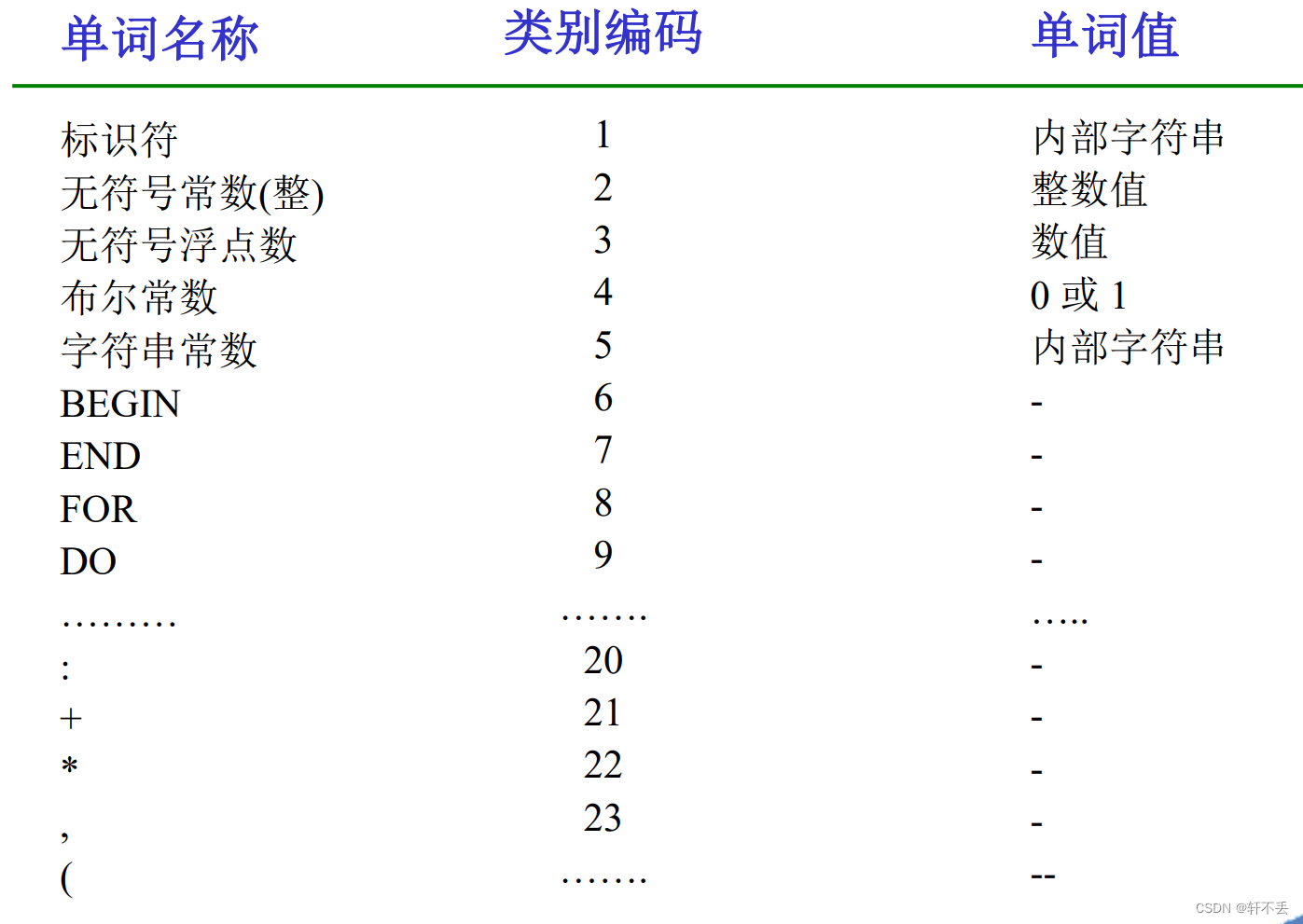
符号根据文法的非终结符确定
二、(有穷状态)自动机
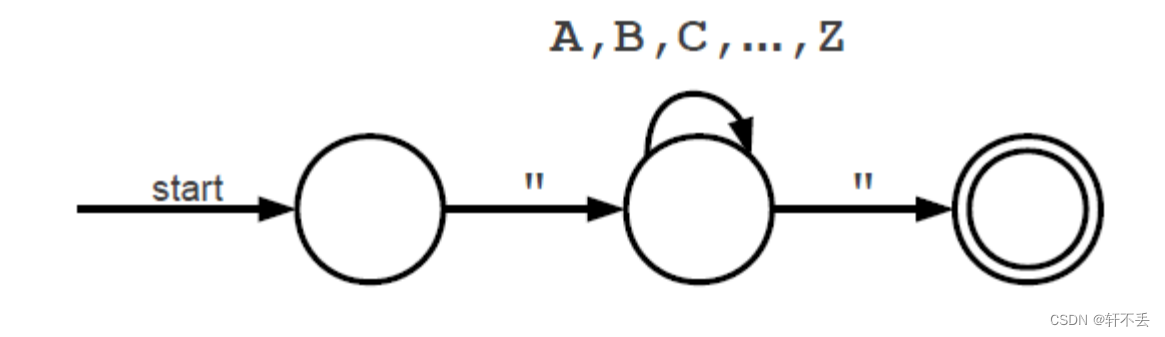
(有穷状态)自动机:是另一种抽象
Σ
∗
Σ^*
Σ∗上的语言
L
L
L 的方法
字母表
Σ
Σ
Σ,状态集
Q
Q
Q,初始状态
s
s
s,状态转移函数,接受状态
根据文法建立自动机
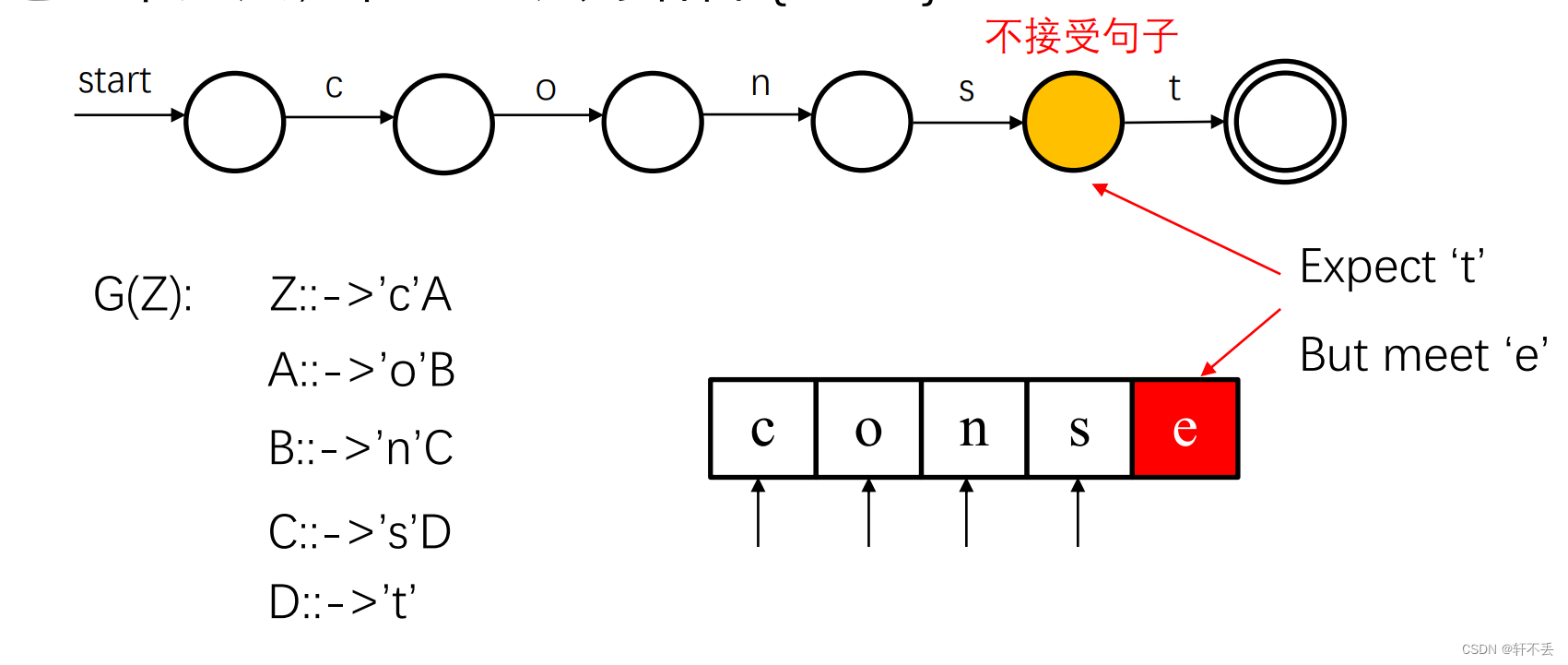
多自动机同时工作
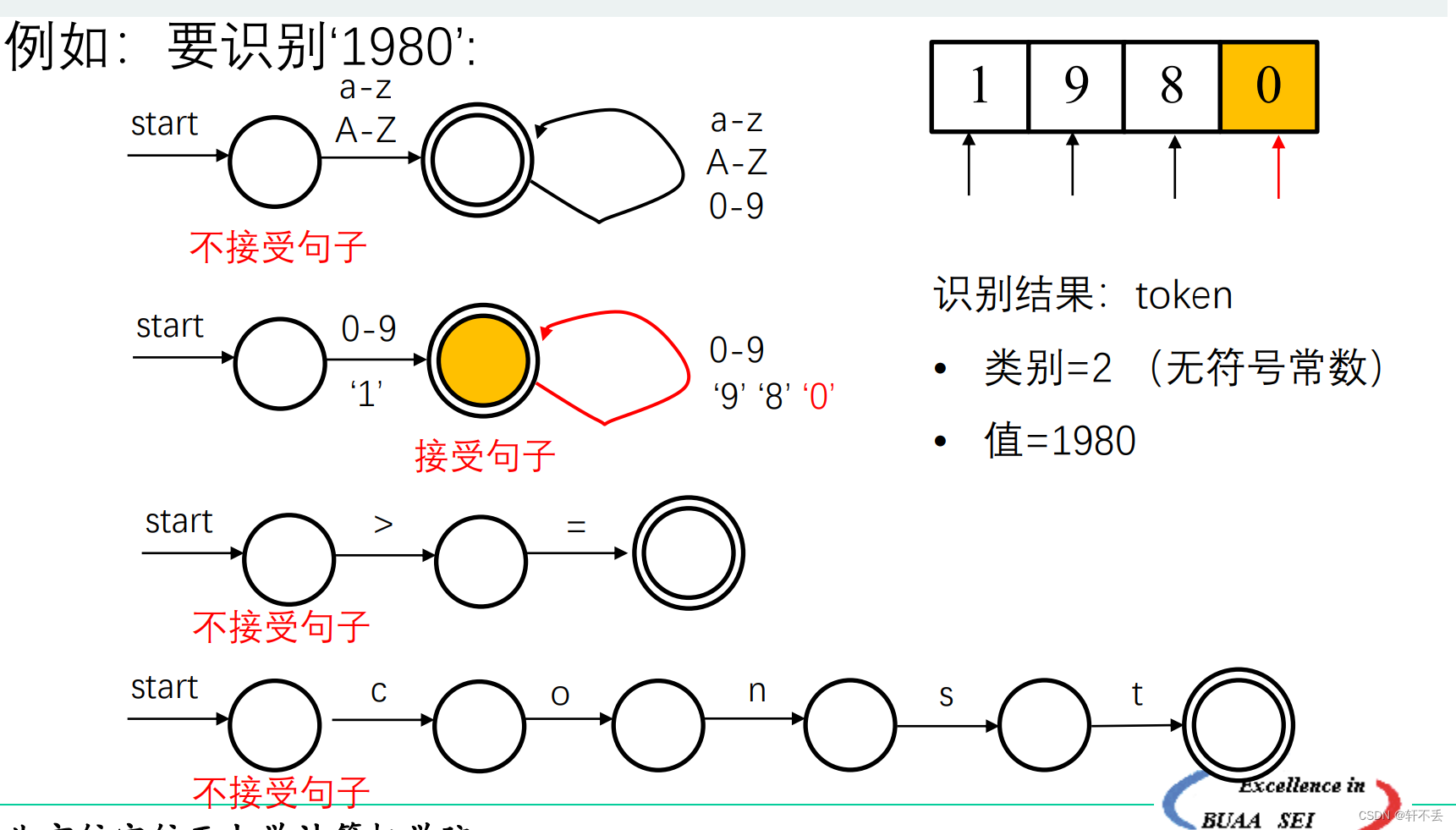
如果一个单词同时满足多个自动机,那么通常我们选择 最长的匹配,或者显示指定优先级(如:保留字优先)
三、正则文法和状态图
词法分析主要针对的是3型文法。
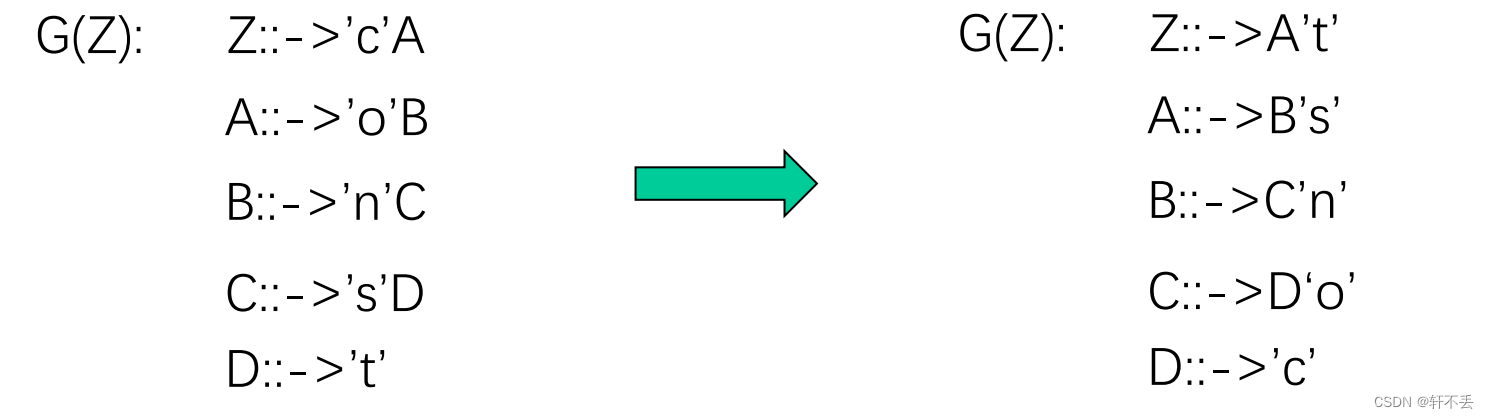
左线性文法状态图的画法:
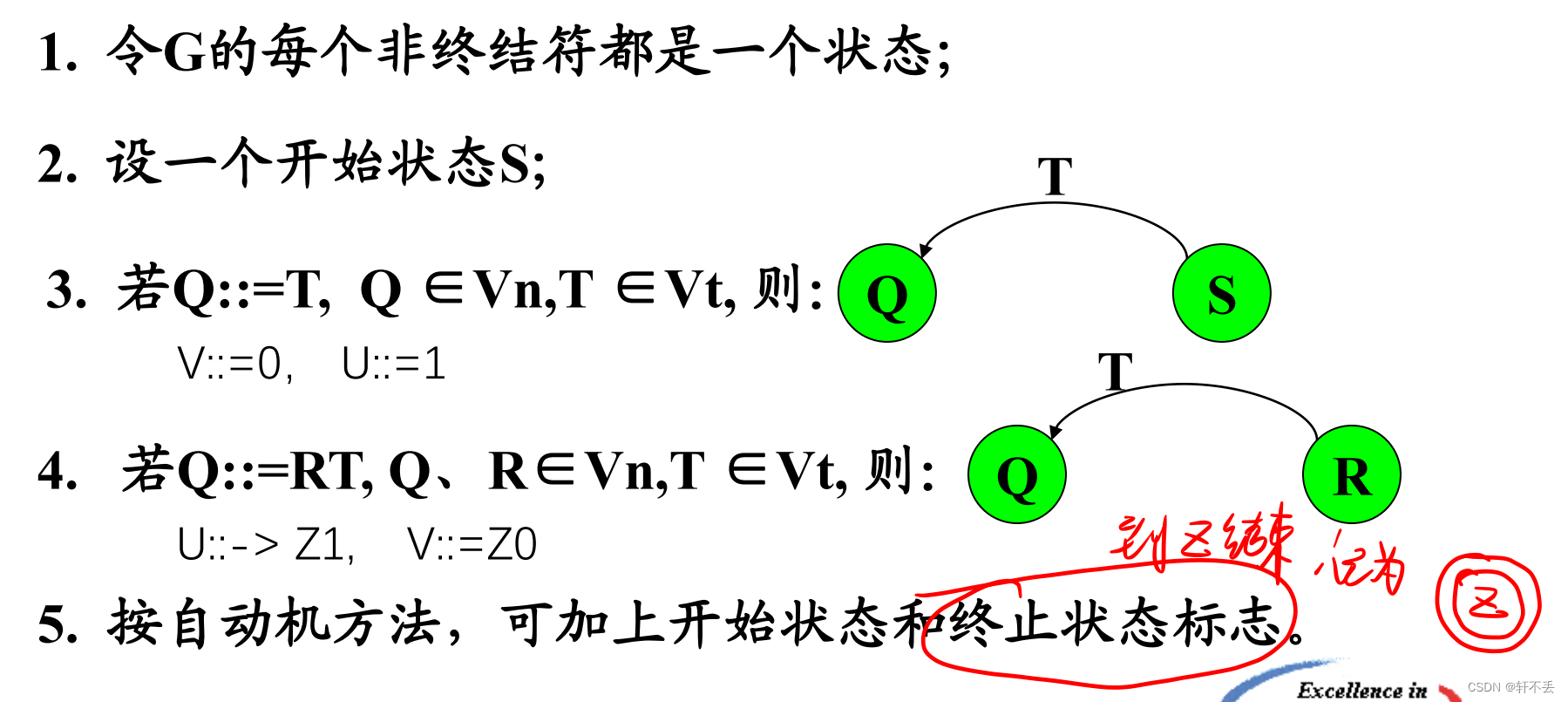
例如:
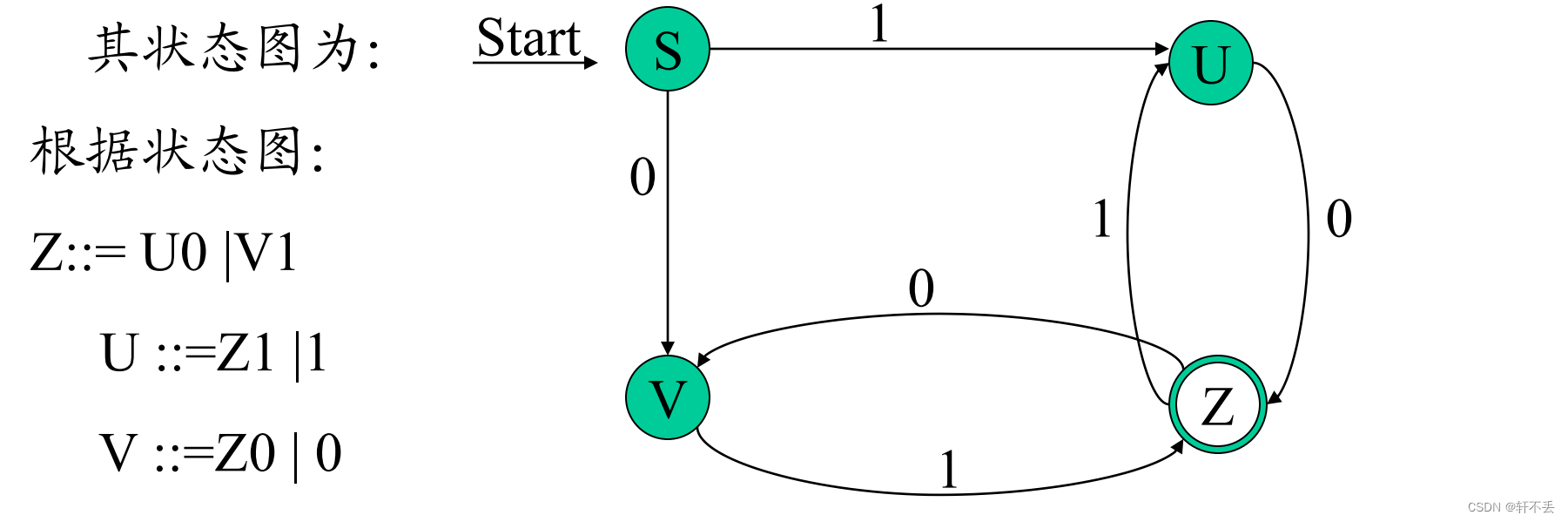
因此:给定左线性文法,我们可以得到状态图。
左右线性文法等价:从左(右)线性文法,可以构造等价的右(左)线性文法
四、词法分析程序流程

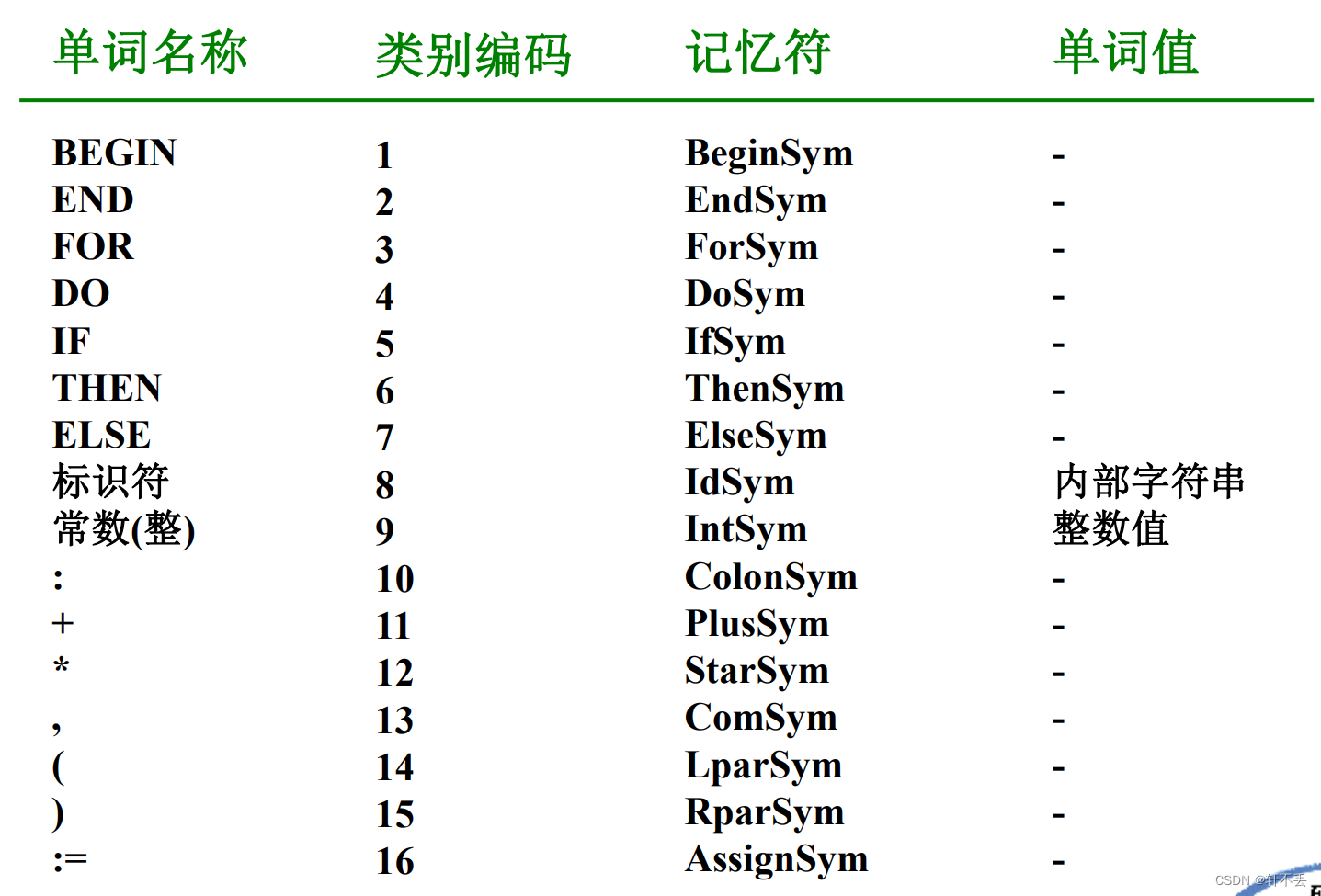
1、单词及内部表示
保留字和分界符采用一符一类
2、词法分析程序需要引用的公共(全局)变量和过程

UnGetCH一般是程序结束时会多读一个字符(判断是否结束),此时需要回退一个单位。
五、自动机
1、DFA(确定的有穷状态自动机)
一个确定的有穷自动机(DFA)M是一个五元式: M = ( S , Σ , δ , s 0 , Z ) M=(S, Σ,δ, s_0, Z) M=(S,Σ,δ,s0,Z)
- S —有穷状态集
- Σ —输入字母表
- δ —映射函数(也称状态转换函数)
S × Σ → S S×Σ→S S×Σ→S
δ ( s , a ) = s ’ , s , s ’ ∈ S , a ∈ Σ δ(s,a)=s’ , s, s’ ∈S, a∈Σ δ(s,a)=s’,s,s’∈S,a∈Σ - s 0 s_0 s0—初始状态 s 0 ∈ S s_0 ∈S s0∈S
- Z—终止状态集
Z
⊆
S
Z \subseteq S
Z⊆S
例如:
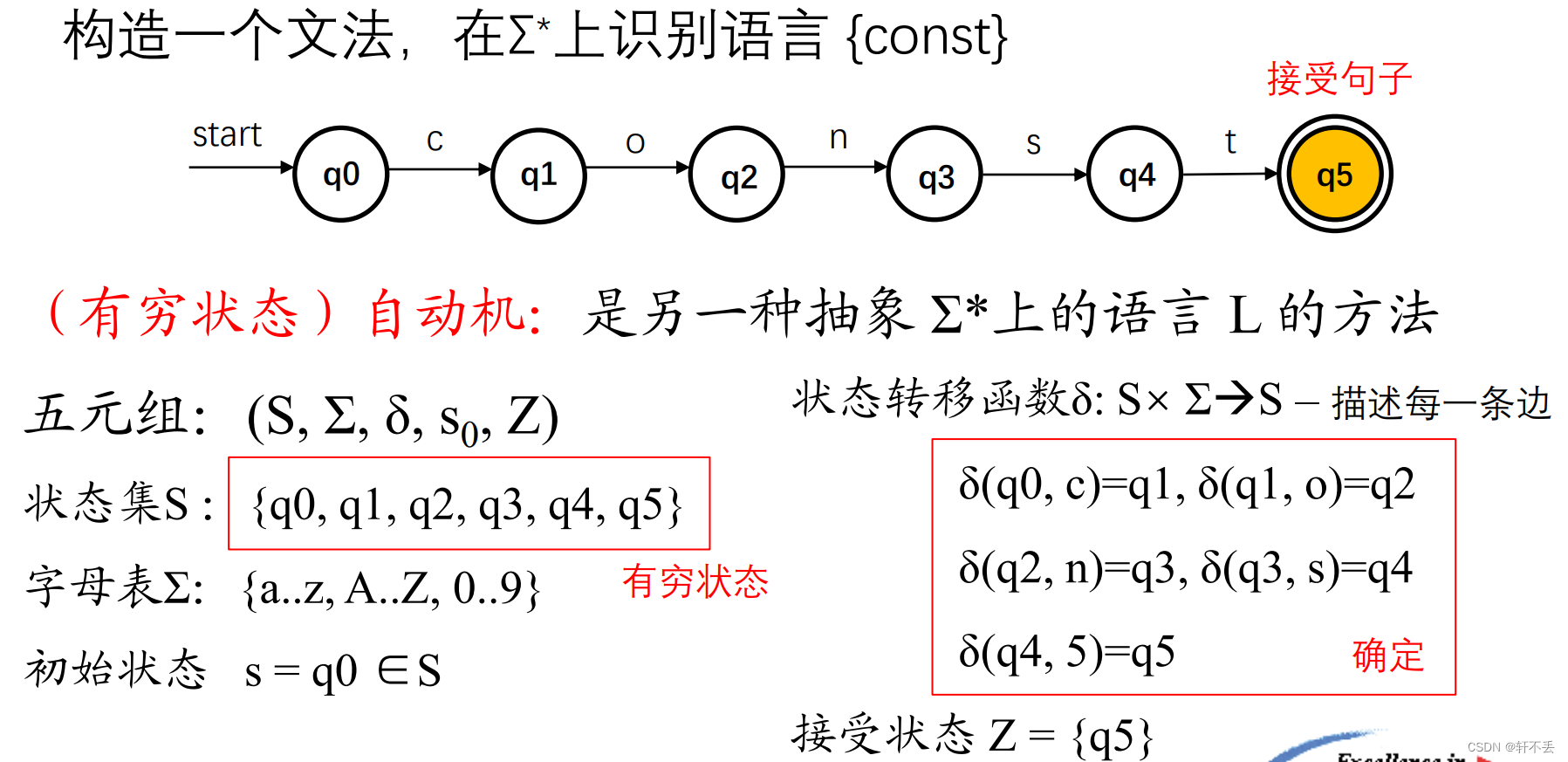
2、NFA(不确定的有穷自动机)
若δ是一个多值函数,且输入可允许为ε,则有穷自动机是不确定的,即在某个状态下,对于某个输入字符存在多个后继状态。
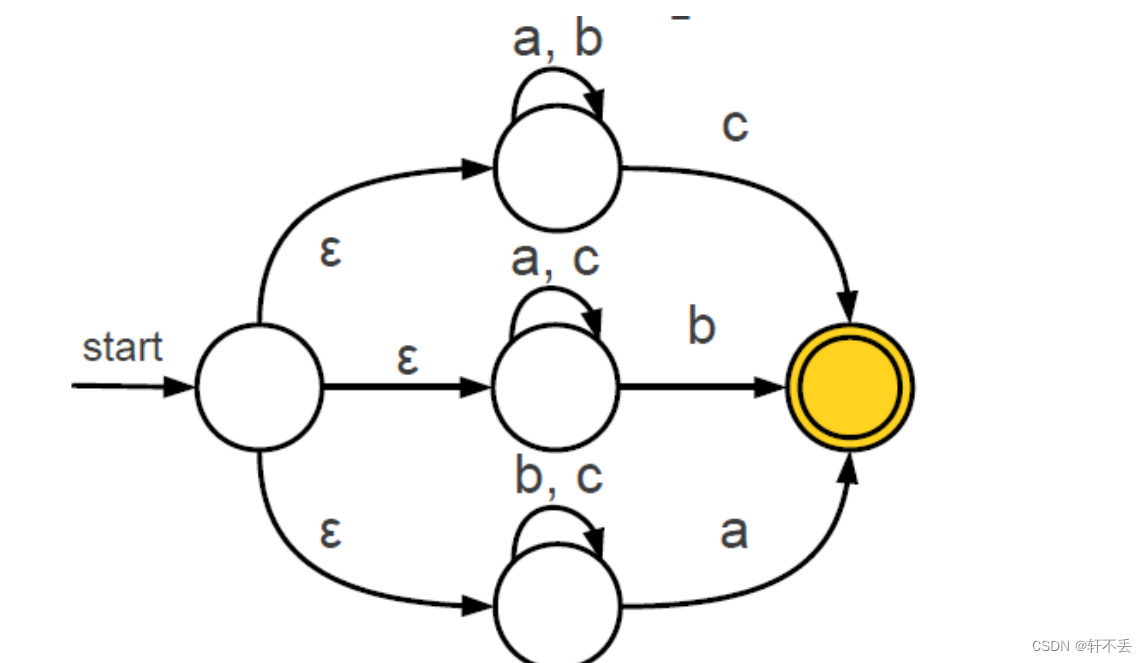
正则表达式
(
R
)
(R)
(R)
R
∗
R^*
R∗
R
1
R
2
R1R2
R1R2
R
1
∣
R
2
R1|R2
R1∣R2
{}的作用和*一样

优先级:
先
∗
,
后•
,
最后
∣
先*, 后 •, 最后 |
先∗,后•,最后∣
给定正则,构造NFA
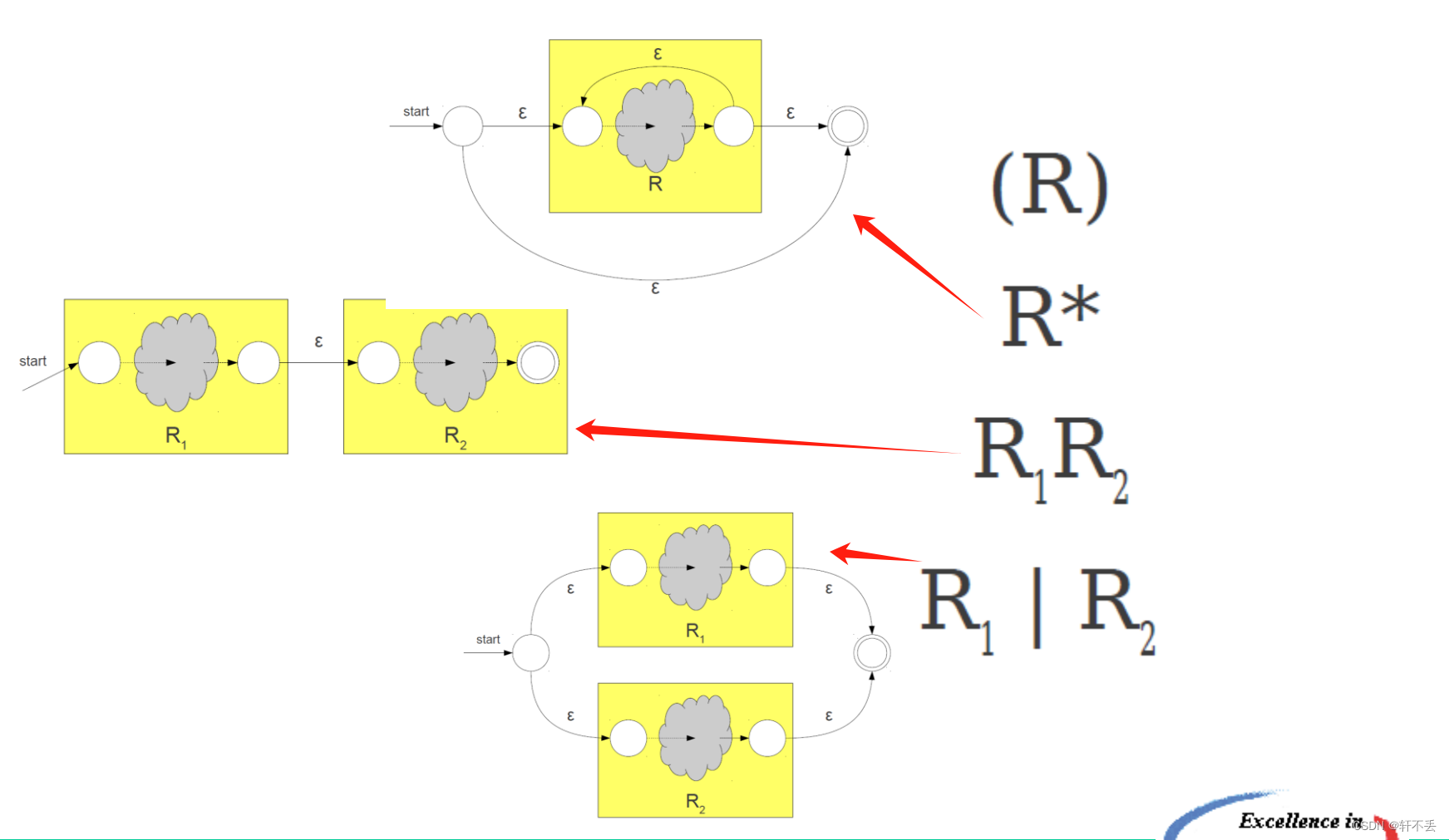
3、NFA确定化
1)一些概念
- 集合
I
I
I的
ε
ε
ε-闭包
令I是一个状态集的子集,定义 ε − c l o s u r e ( I ) ε-closure(I) ε−closure(I)为:
1)若 s ∈ I s∈I s∈I,则 s s s∈ ε − c l o s u r e ( I ) ε-closure(I) ε−closure(I);
2)若 s ∈ I s∈I s∈I,则从 s s s出发经过任意条ε弧能够到达的任何状态都属于 ε − c l o s u r e ( I ) ε-closure(I) ε−closure(I)。
状态集 ε − c l o s u r e ( I ) ε-closure(I) ε−closure(I)称为 I I I的 ε ε ε-闭包。 - 令
I
I
I是
N
F
A
M
’
NFA M’
NFAM’的状态集的一个子集,
a
∈
Σ
a∈Σ
a∈Σ
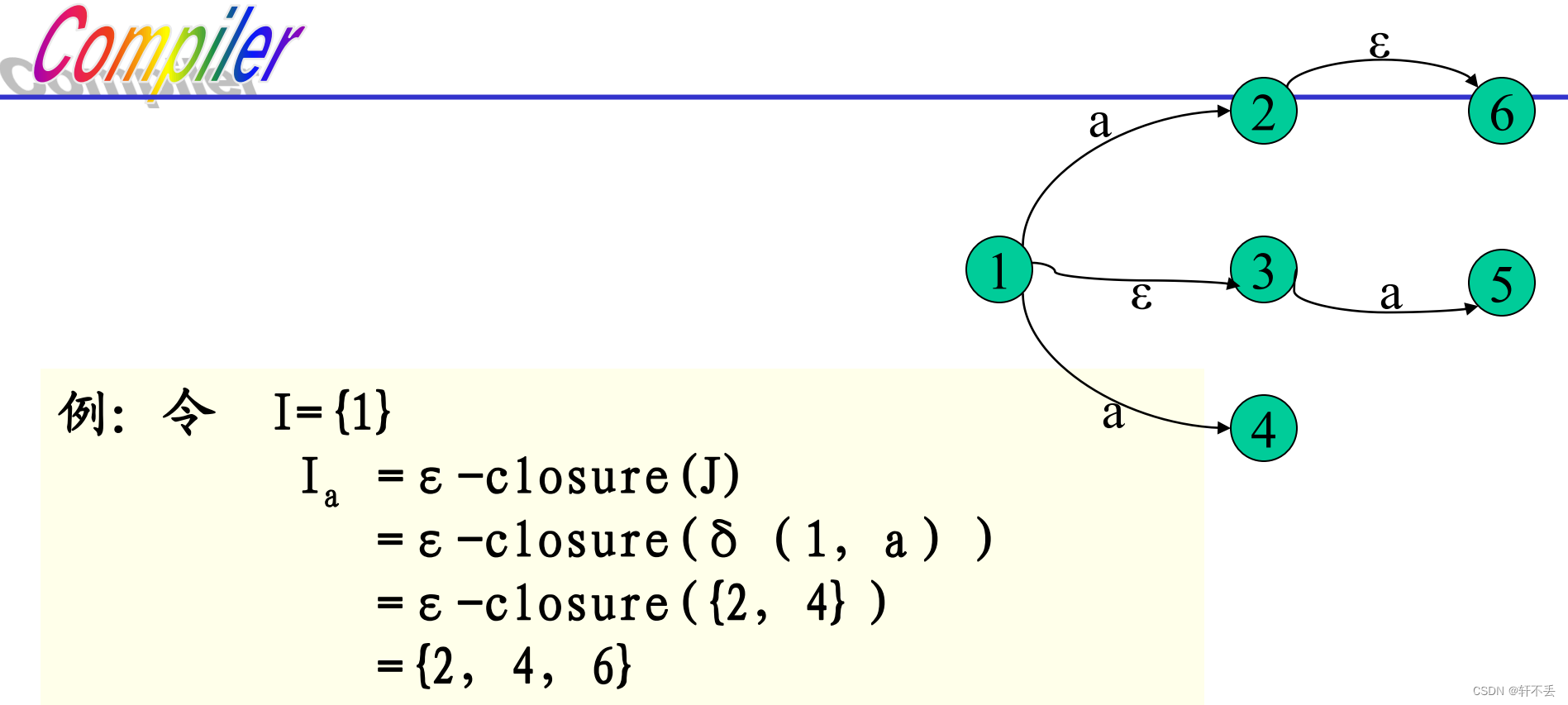
定义: I a = ε − c l o s u r e ( J ) I_a=ε-closure(J) Ia=ε−closure(J)
其中 J = ∪ δ ( s , a ) J = ∪δ(s,a) J=∪δ(s,a)
J J J是从状态子集I中的每个状态出发,经过标记为 a a a的弧而达到的状态集合。
I a I_a Ia是状态子集,其元素为J中的状态,加上从 J J J中每一个状态出发通过 ε ε ε弧到达的状态。
注意状态转移后若还能通过 ε ε ε弧到达的状态,也需要包含进去.
2)确定化过程
根据定义不断循环,即可得到状态转换矩阵。
得到的新状态不断递归。
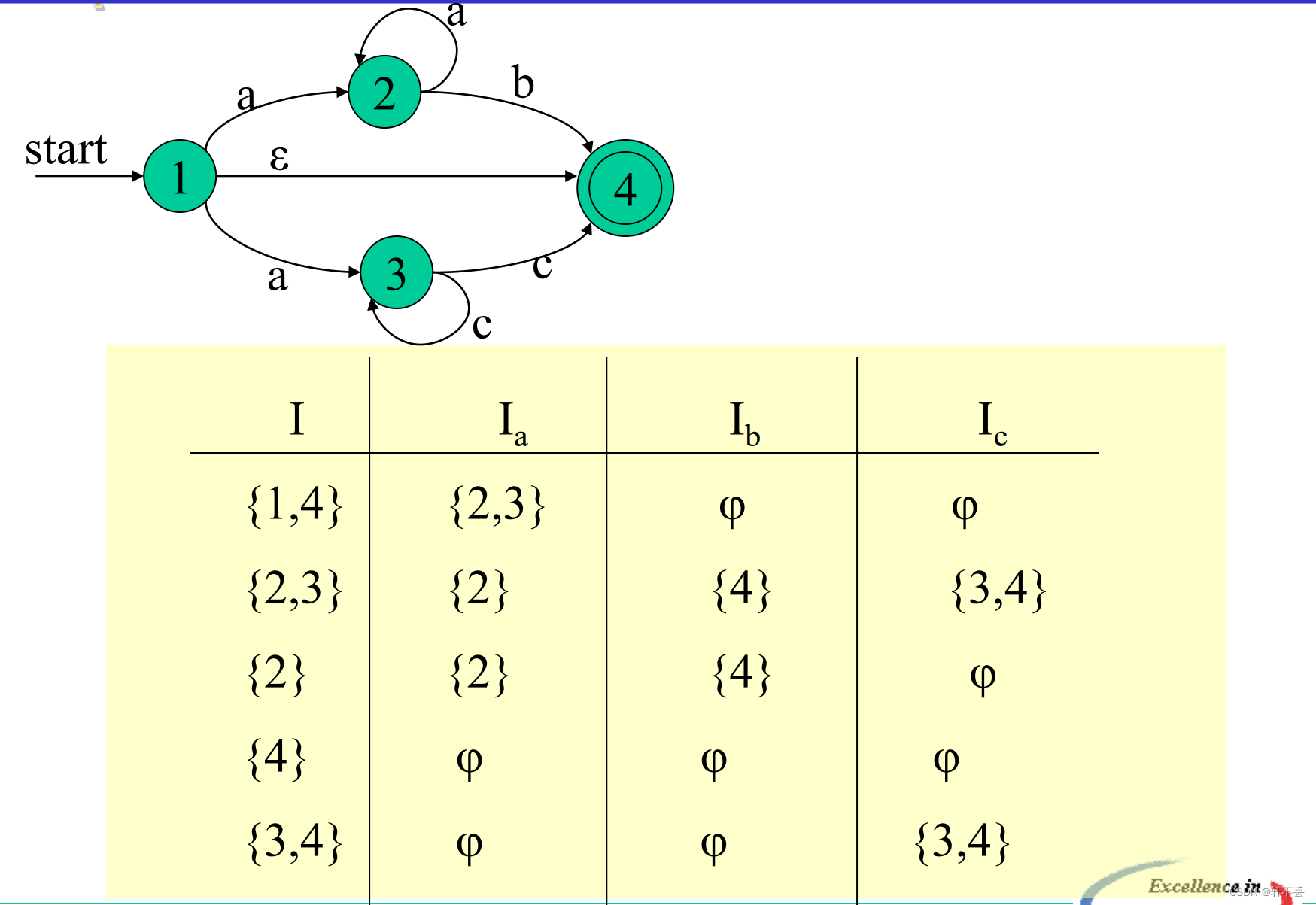
将求得的状态转换矩阵重新编号.
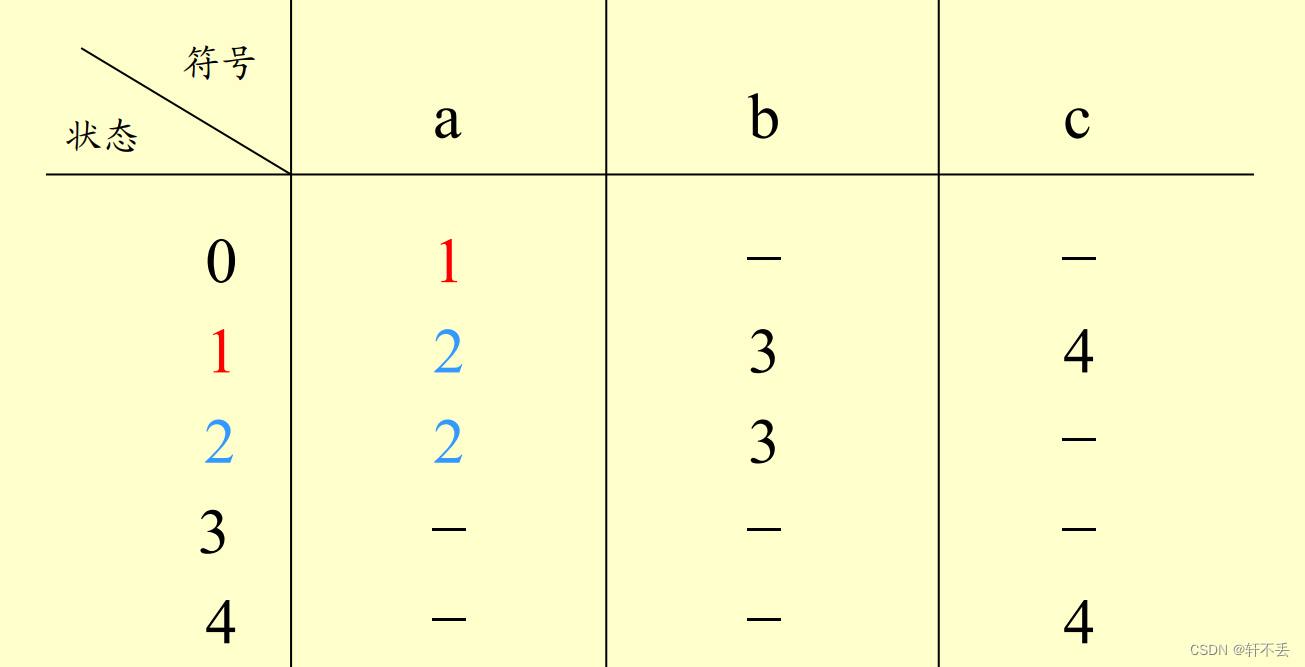
画出新的状态转移图。
注意:原初始状态的
ε
−
c
l
o
s
u
r
e
ε-closure
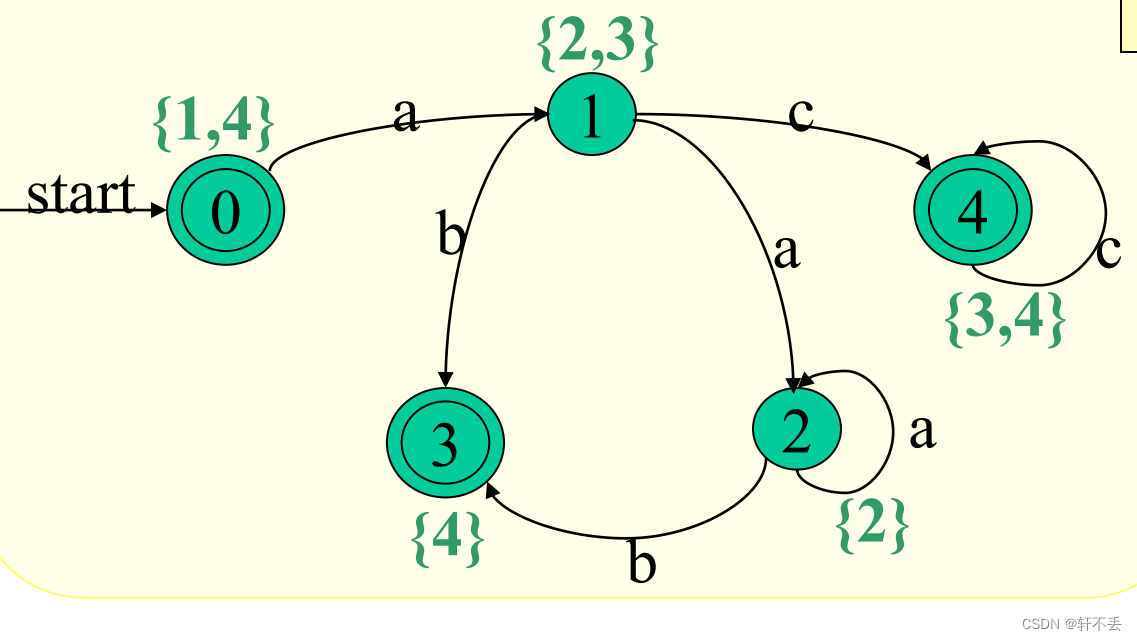
ε−closure为DFA M的初态
包含原终止状态4的状态子集为
D
F
A
M
DFA M
DFAM的终态,因此上述中3和4是终态。
4、DFA的极简化(极小化)
对于任一个DFA,存在一个唯一的状态最少的等价的DFA。
一个有穷自动机是化简的 <=> 它没有多余状态并且它的状态中没有两个是互相等价的。
一个有穷自动机可以通过消除多余状态和合并等价状态而转换成一个最小的与之等价的有穷自动机
1)一些概念
- 有穷自动机的多余状态:
从该自动机的开始状态出发,任何输入串也不能到达那个状态。
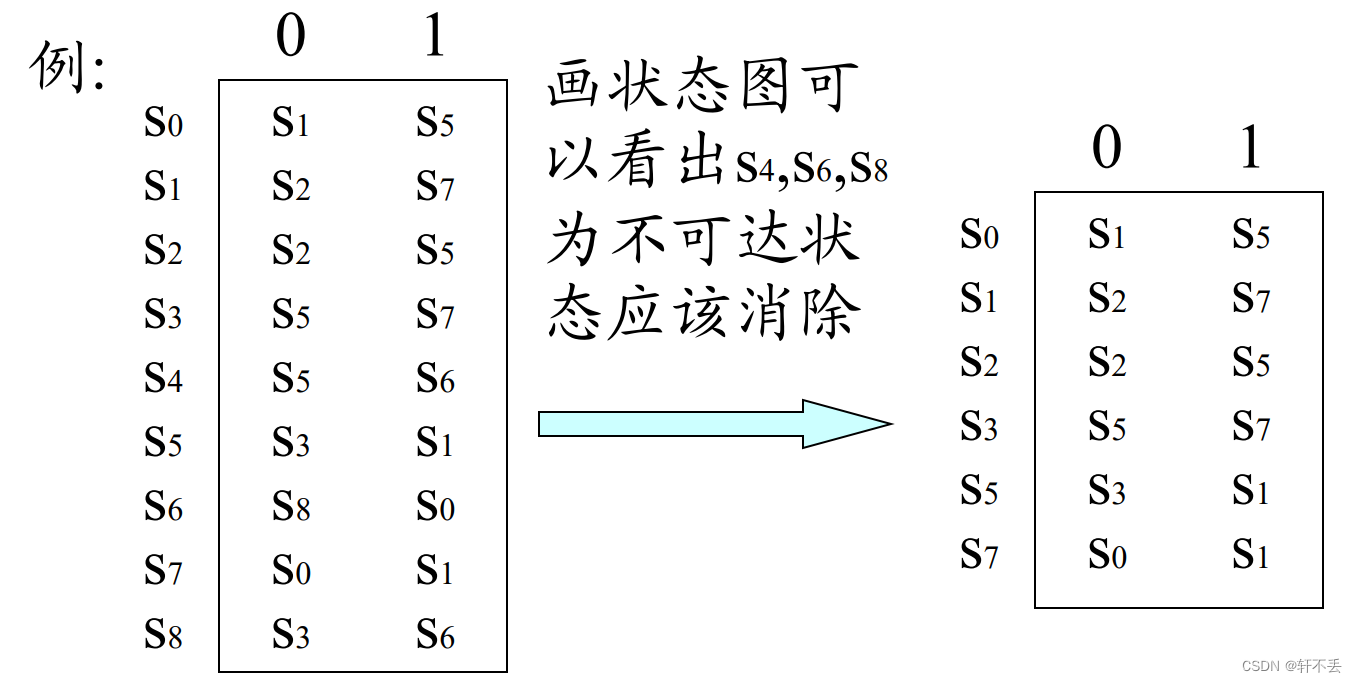
- 等价状态:状态s和状态t的等价条件是
一致性条件:状态s和t必须同时为可接受状态或不接受状态
蔓延性条件:对于所有输入符号,状态s和t必须转换到等价的状态里。
2)矩阵法
状态合并例题求解:
首先画出状态矩阵,对角线不用看(本来就是一个状态)
只要看一半部分就行(上半部分和下半部分是对应的)
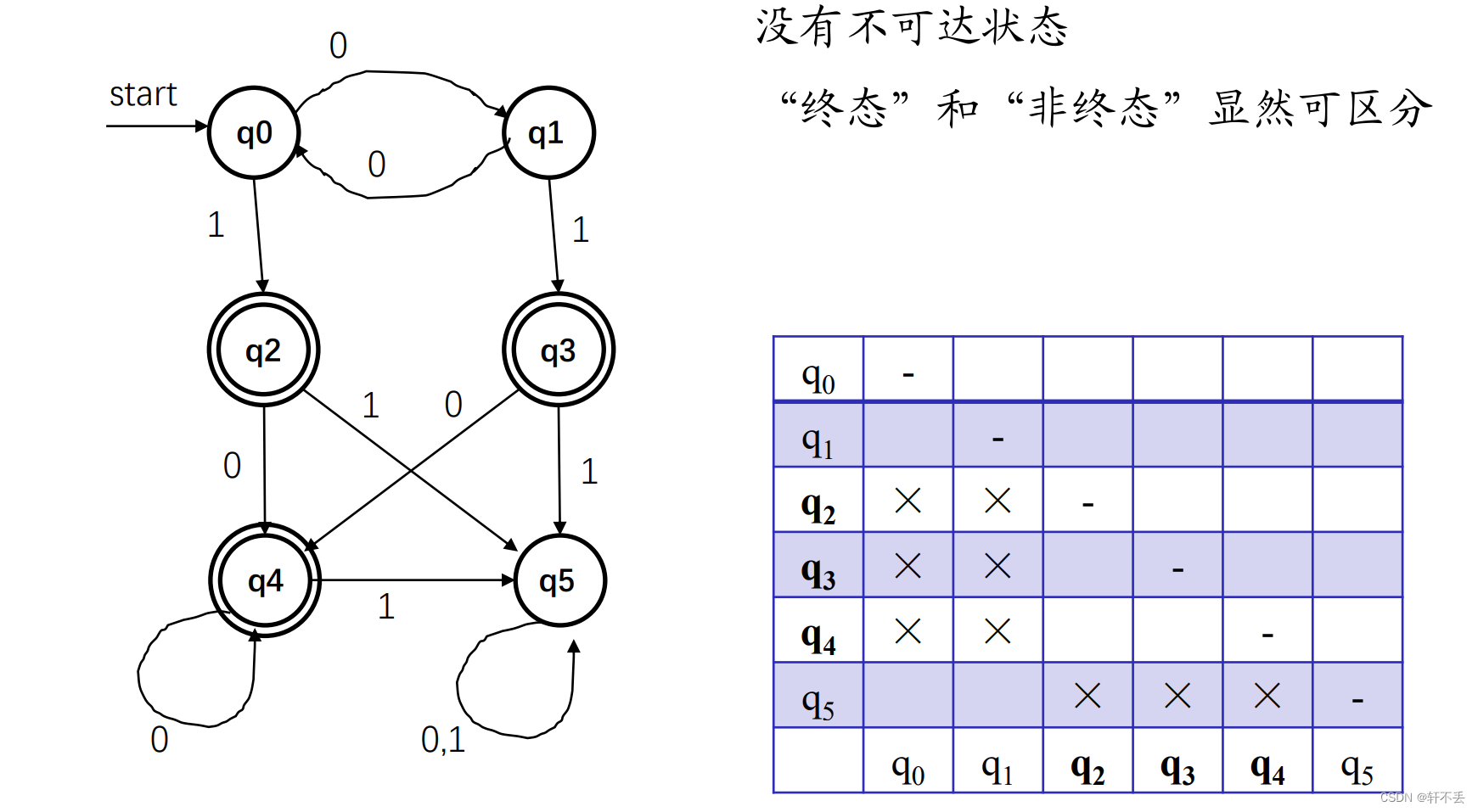
终态和非终态一定不能合并
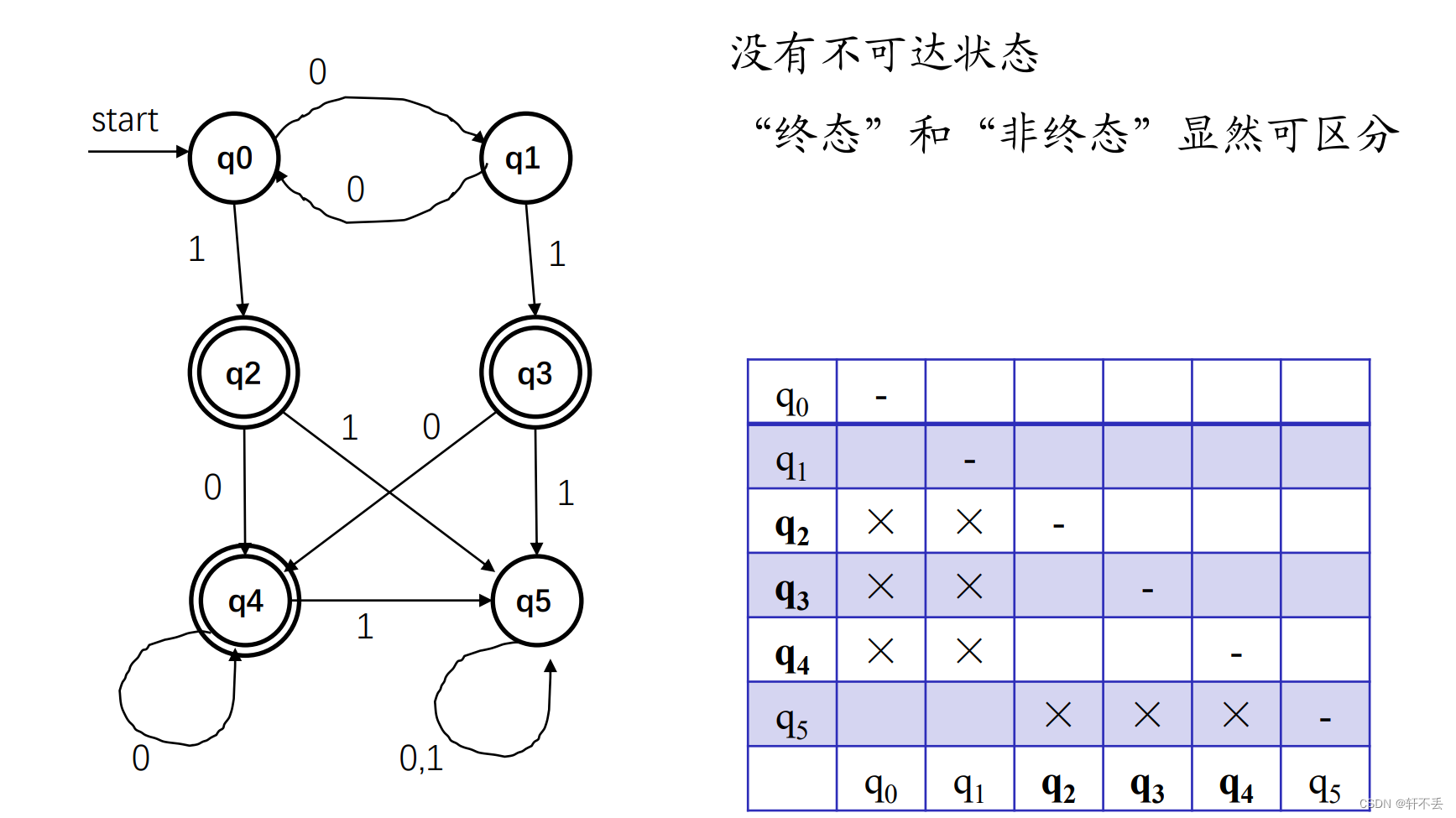
考察
(
q
0
,
q
1
)
(q_0,q_1)
(q0,q1),0进入的是互相,不能作为判断依据(状态合并则等同于同一状态,状态不合并则不是同一状态,没有判断依据)。1进入的状态分别是
q
2
,
q
3
q_2,q_3
q2,q3,若两者属于同一状态则可合并,反之不可,因此此时还不能定夺,继续往下看。
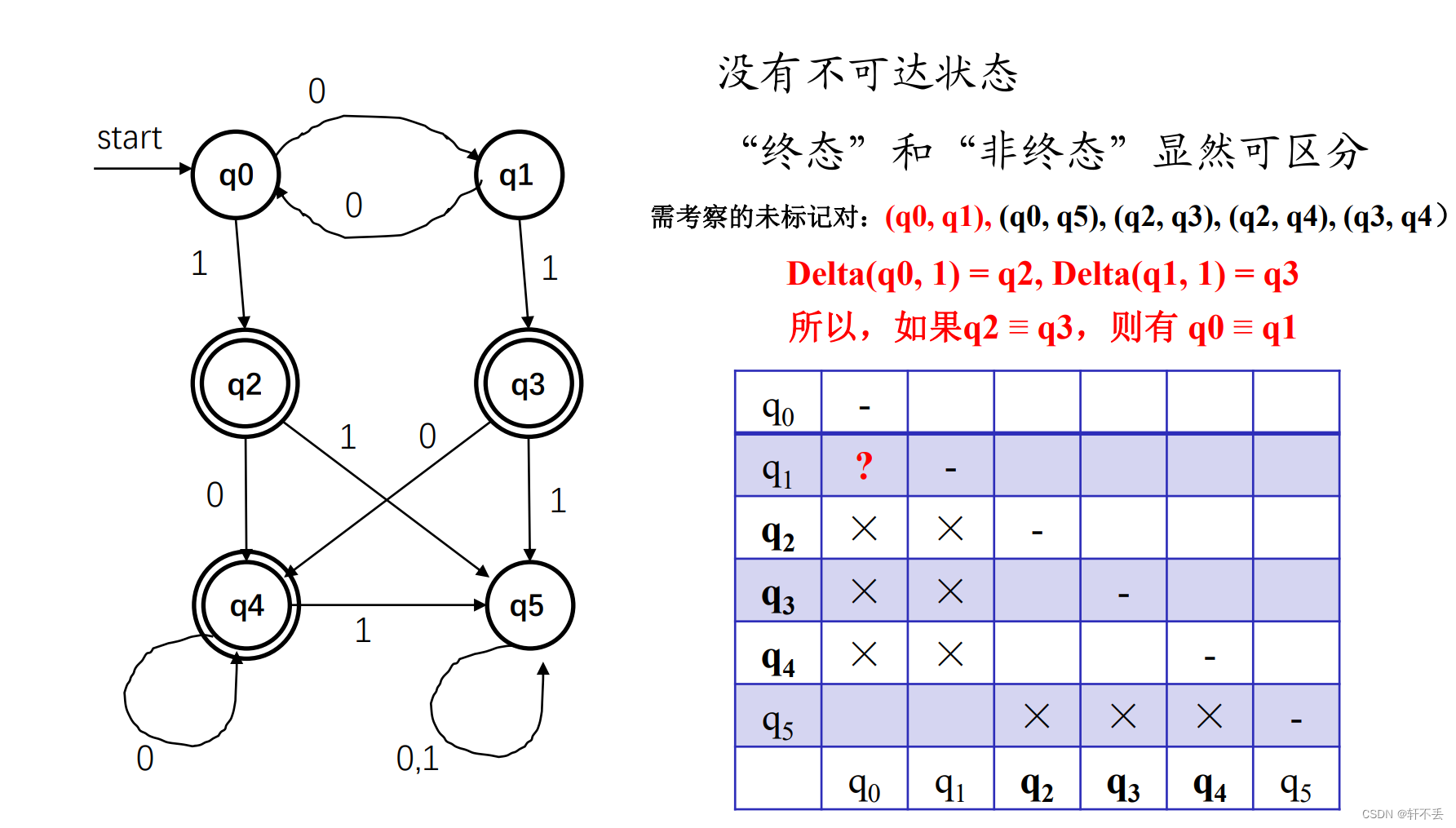
考察
(
q
2
,
q
3
)
(q_2,q_3)
(q2,q3),它们状态转移进去的状态一致,因此合并。因此
(
q
0
,
q
1
)
(q_0,q_1)
(q0,q1)可以合并
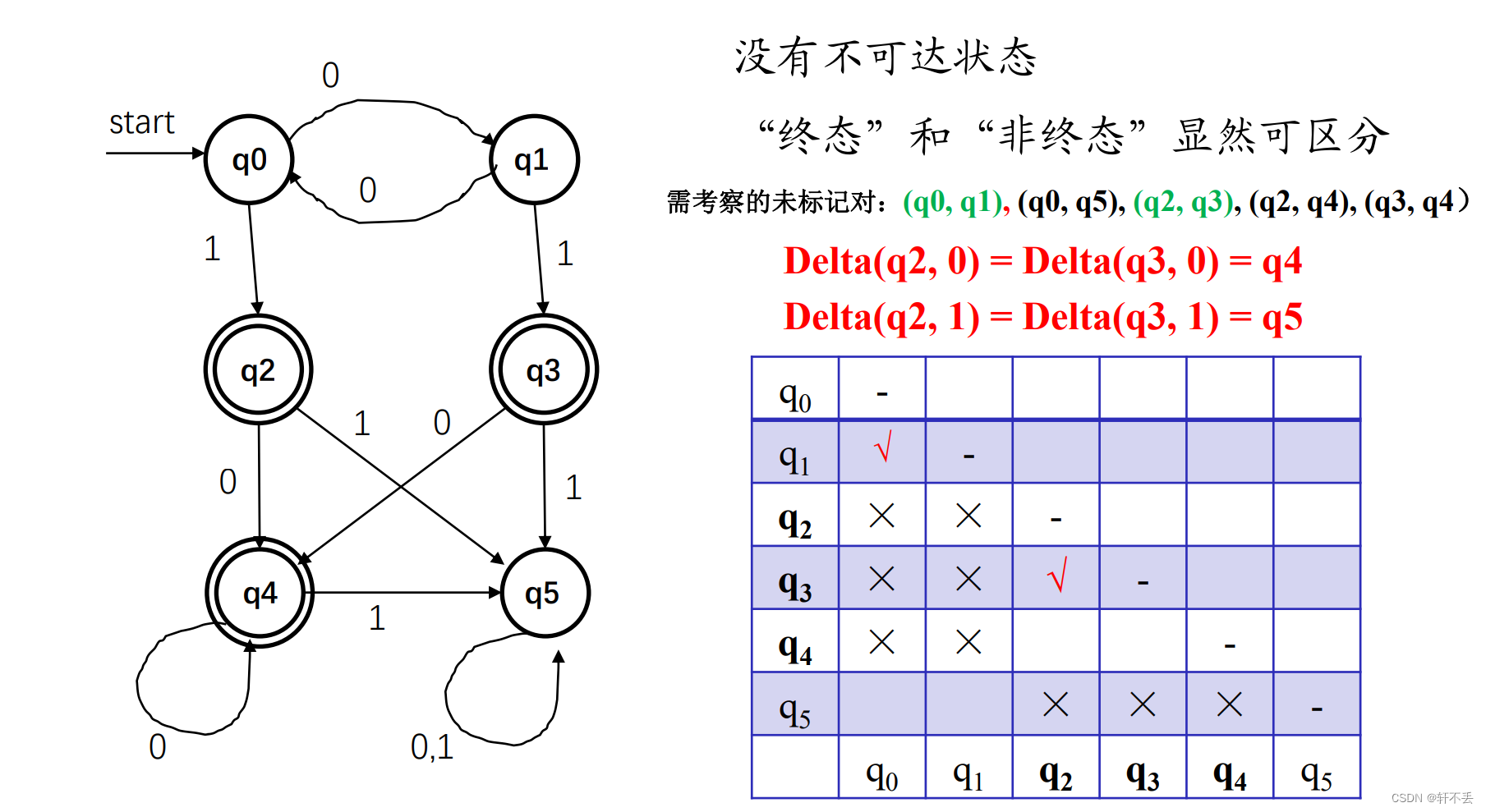
考察
(
q
0
,
q
5
)
(q_0,q_5)
(q0,q5),一个到达终态,另一个到达非终态,显然不能合并
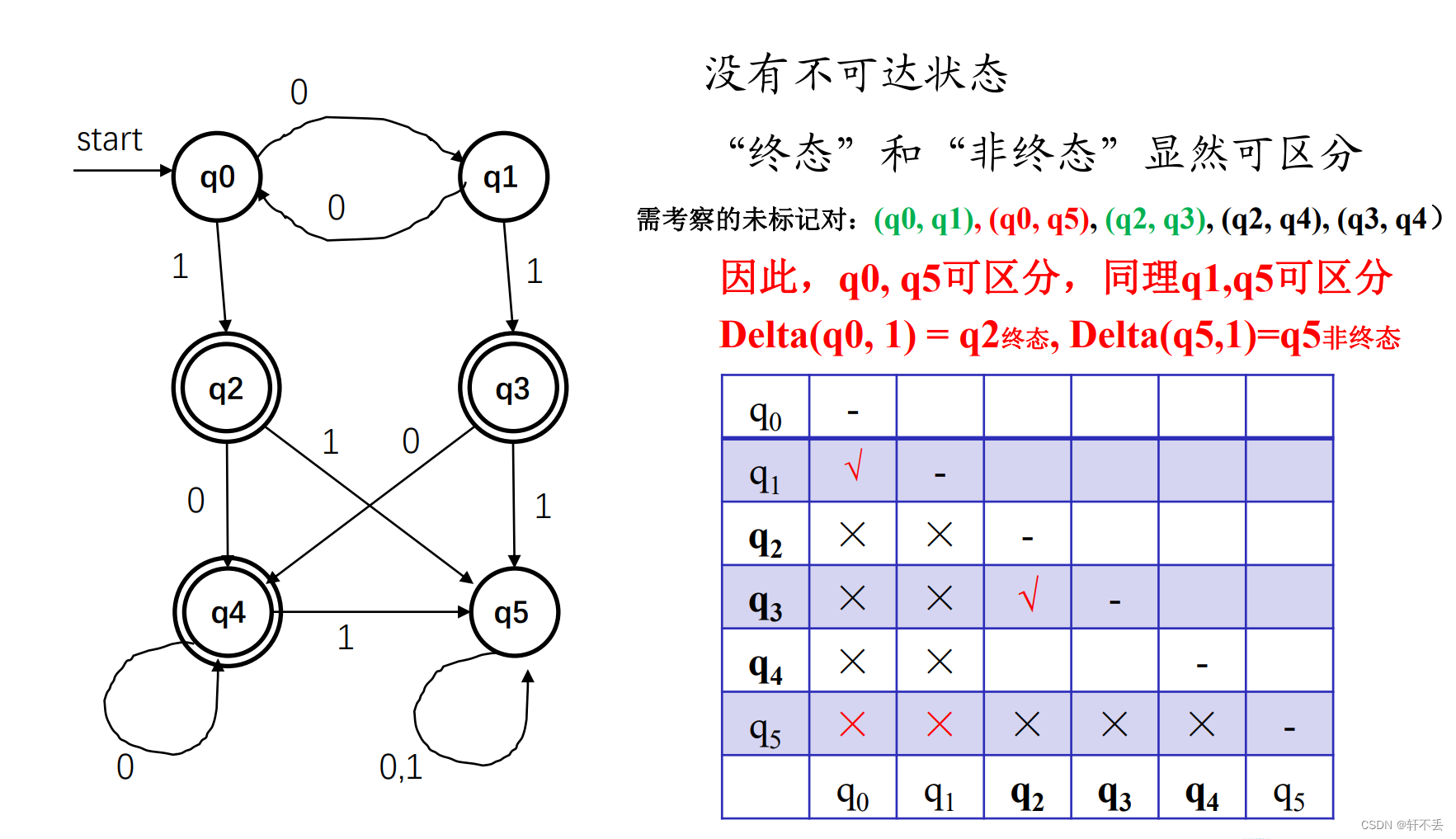
考察
(
q
2
,
q
4
)
(q_2,q_4)
(q2,q4),到达状态相同,可以合并
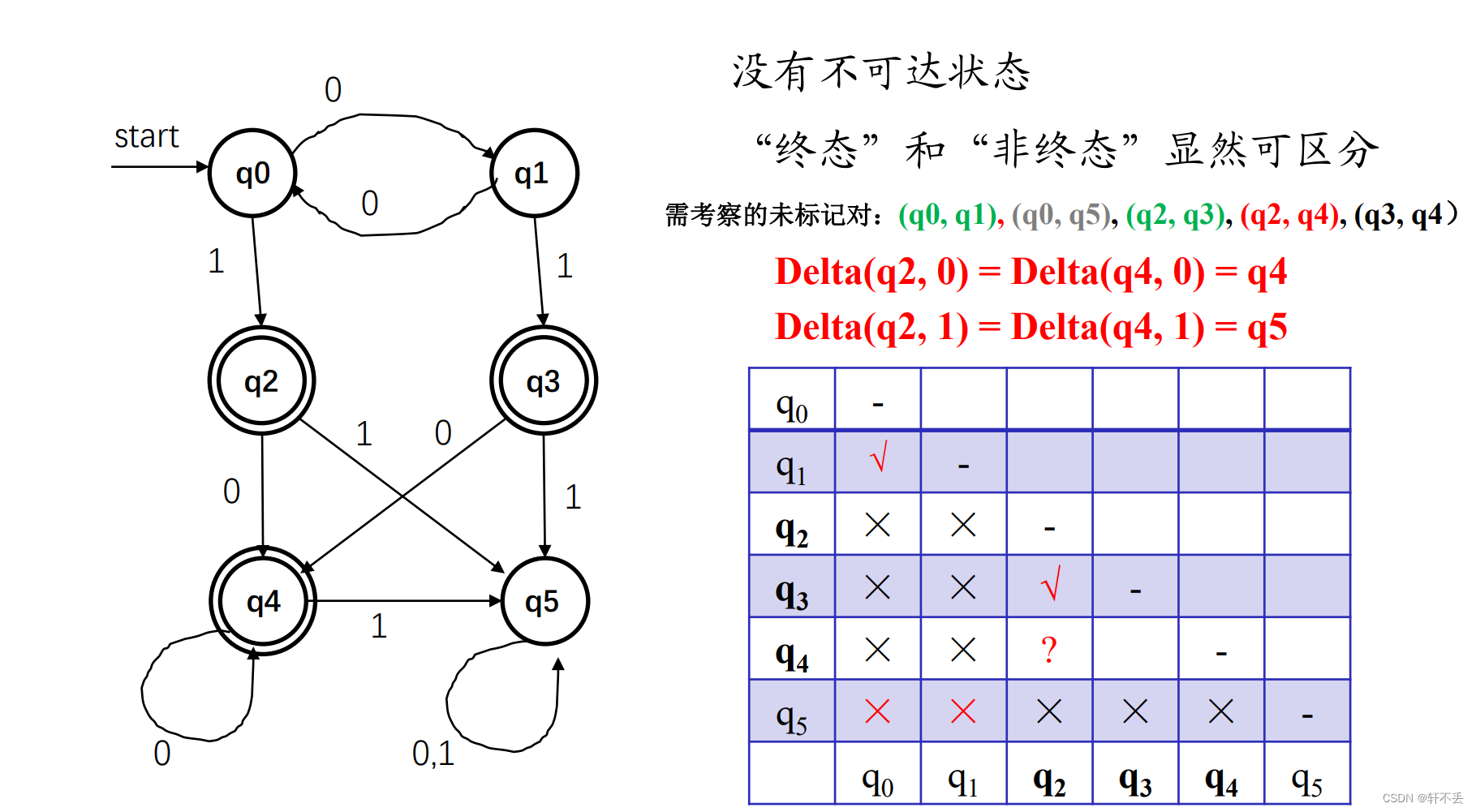
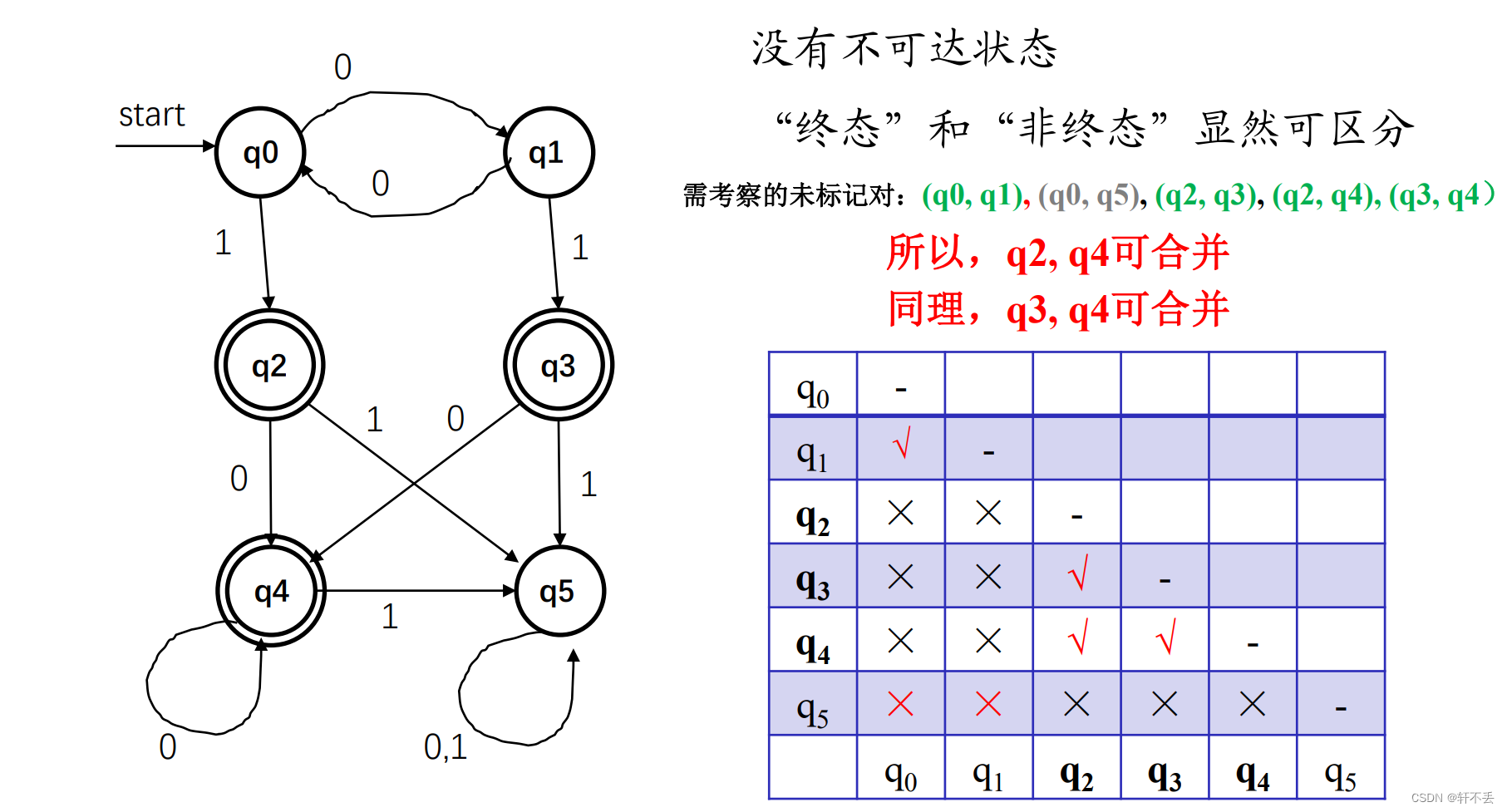
合并结果
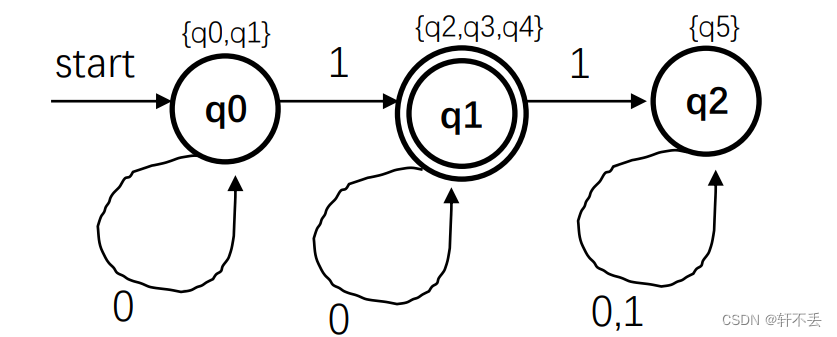
3)分割法
把一个DFA(不含多余状态)的状态分割成一些 不相关的子集,使得任何不同的两个子集状态都是可区别的,而同一个子集中的任何状态都是等价的。
例题求解
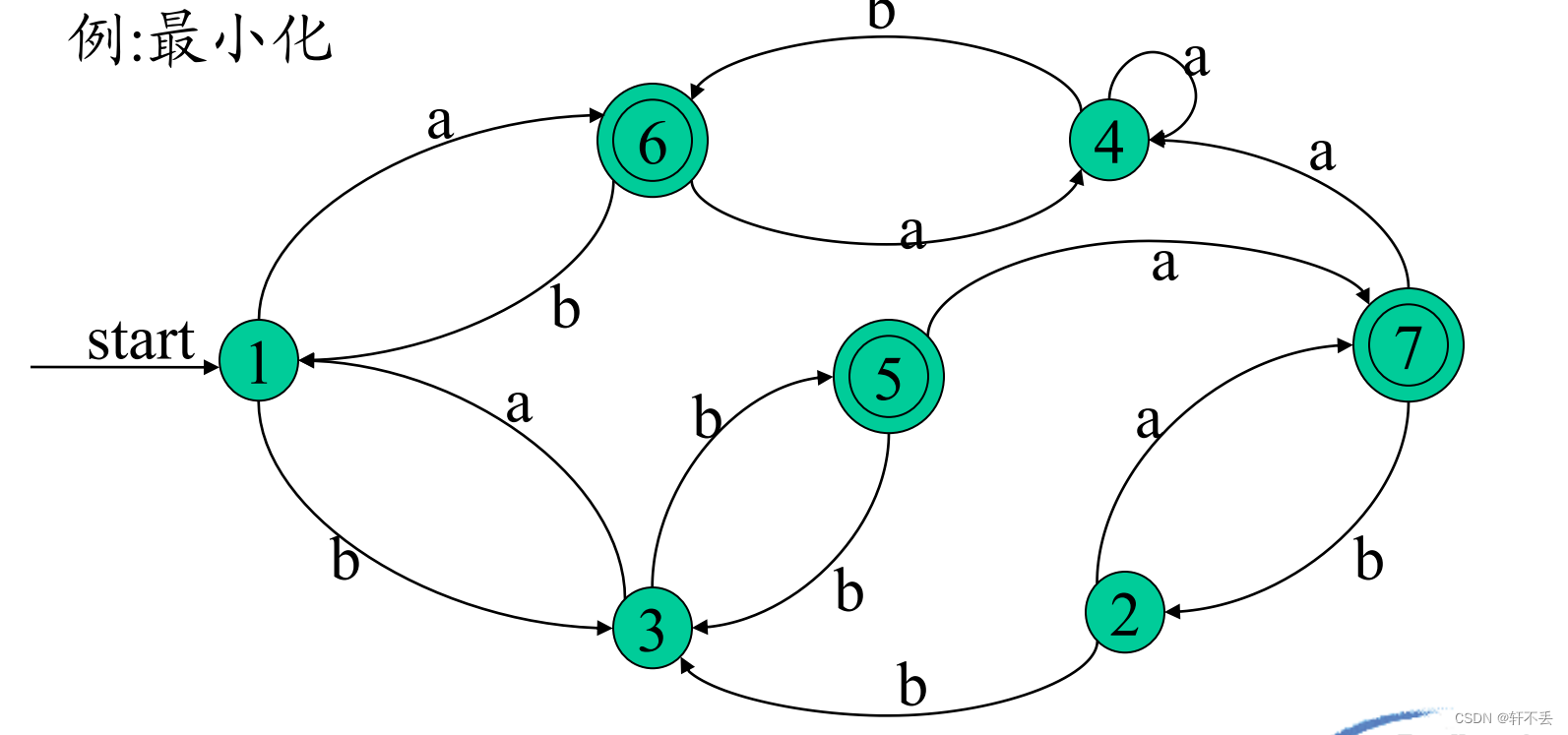
首先区分终态和非终态
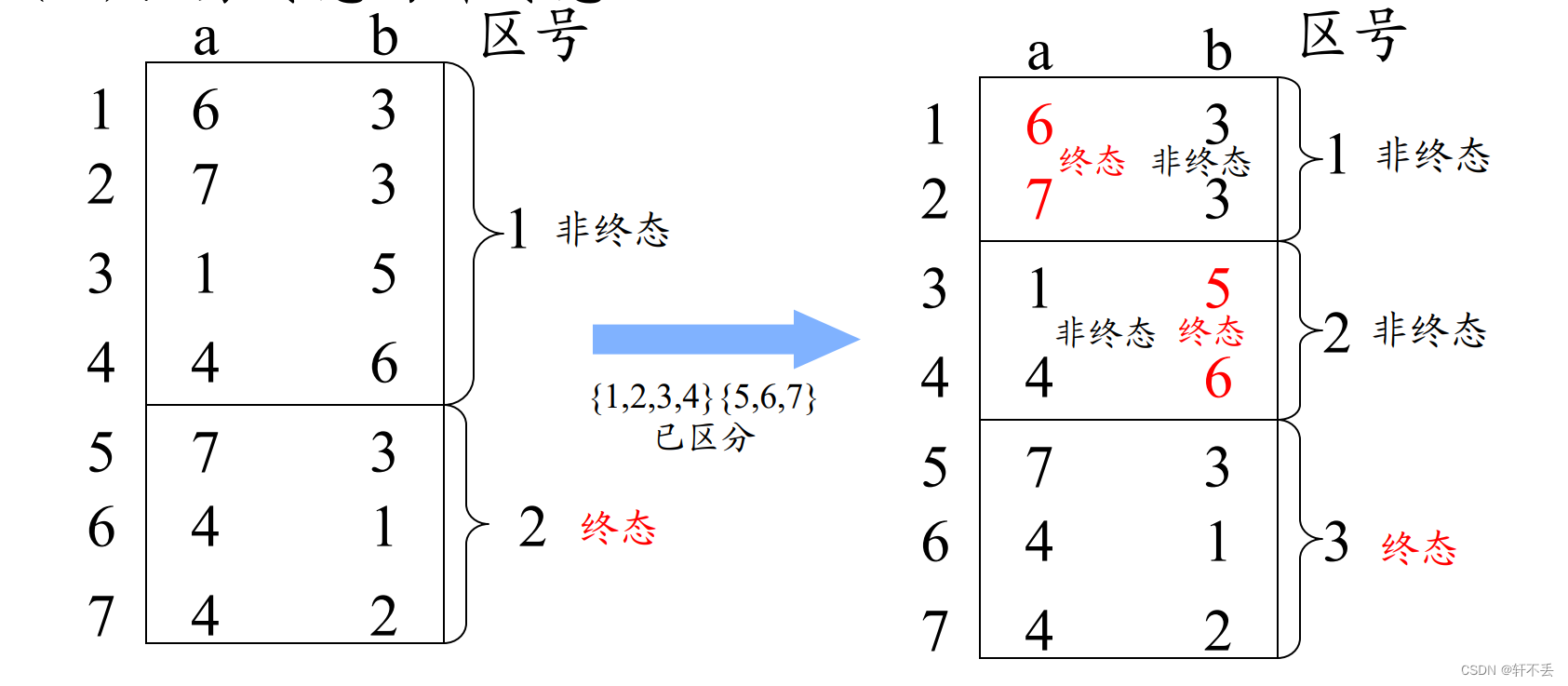
根据区分状态继续分解,直到不能分解为止
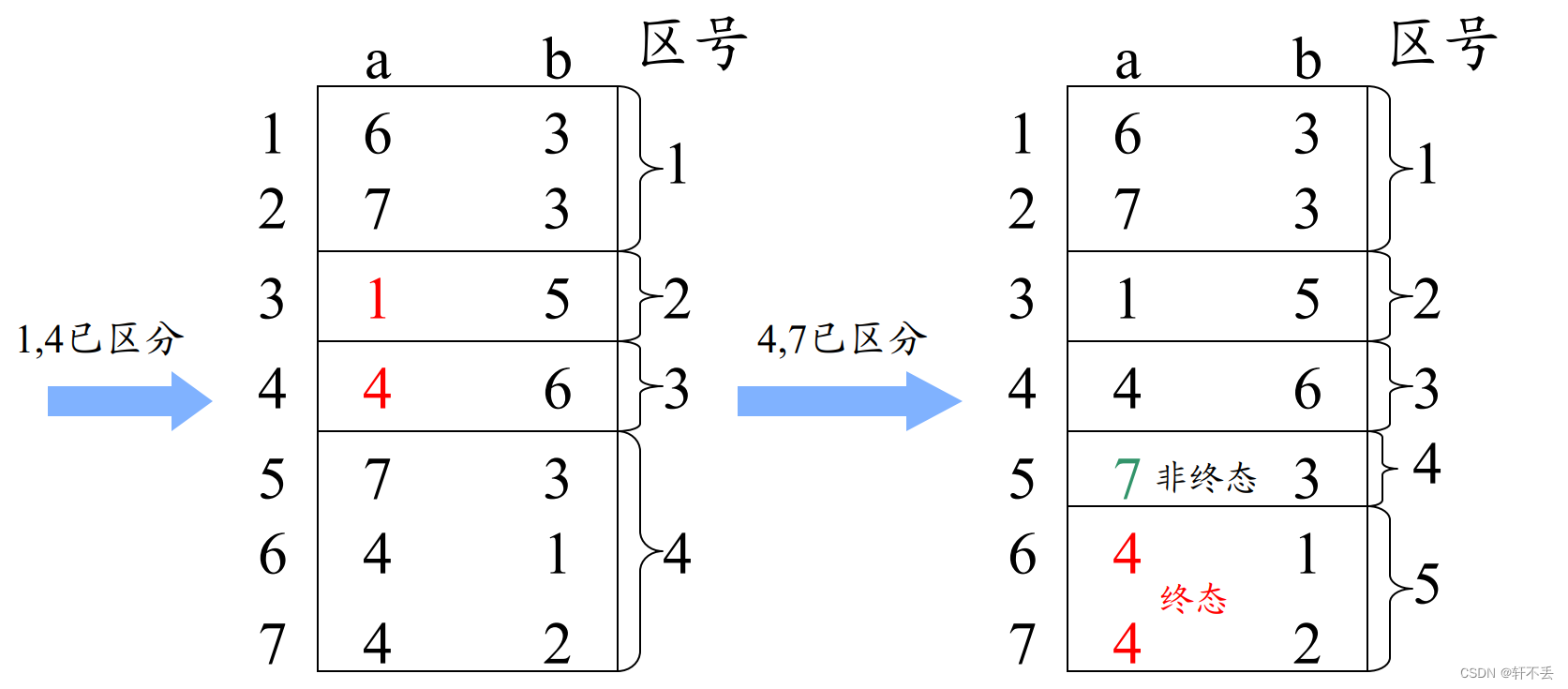
结果如下

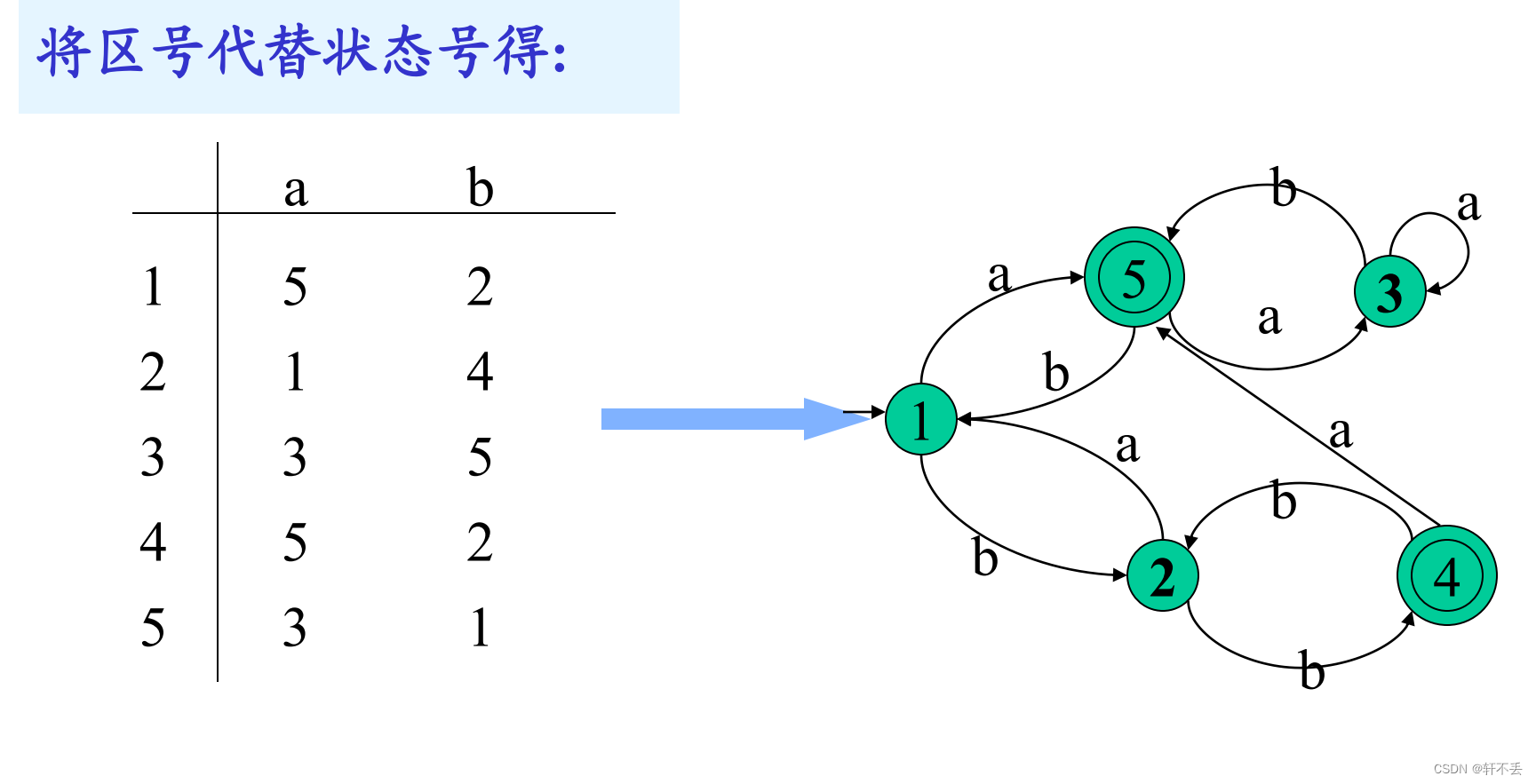
最终得到结果:
六、词法分析的自动化
给定RE → NFA → DFA → 极小化,从而自动生成词法分析程序(正则表达式与DFA的等价性)。
自动化步骤:
- 读LEX源程序,分别生成NFA,用状态图表示为
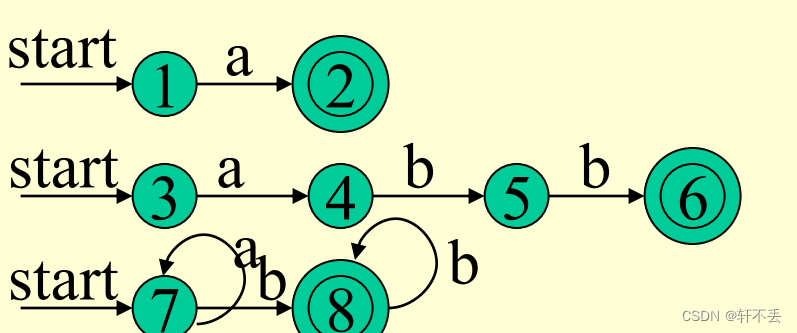
- 合并成一个NFA
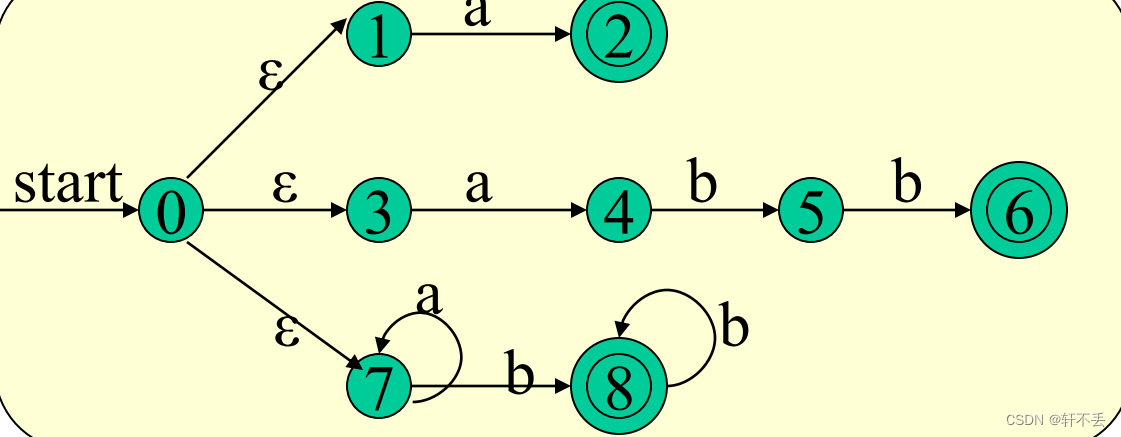
- 确定化