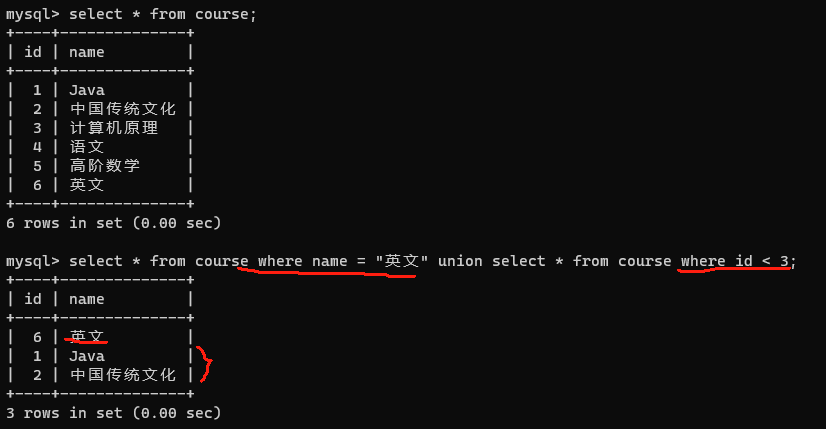
基尔霍夫定律包括基尔霍夫电流定律(KCL)和基尔霍夫电压定律(KVL)。它反映了电路 中所有支路电压和电流所遵循的基本规律,是分析电路的基本定律。基尔霍夫定律与元件 特性构成了电路分析的基础。
电路是由电路元件按照一定的方式组成的系统,因此整个电路的表现既取决于电路中 各个元件的特性,也取决于电路中的元件的连接方式。
名词解释
(1) 支路:电路中每一个二端元件就称为一条支路或电路中通过同一电流的分支。
(2) 节点:电路中各个支路的连接点。
(3) 回路:电路中的任一闭合路径。
(4) 网孔:对平面电路,其内部不含任何支路的回路称 网孔。
网孔是回路,但回路不一定是网孔。例如,图 1-29 中 共有 8 条支路,分析时也可以看成 7 条支路,即 4 和 8 为同 一条支路。图 1-29 中共有 4 个节点,分析时也可以看成 3 个节点,即 4 和 8 之间的连接点不算作节点。图 1-29 中共 有 4 个网孔,10 个回路。

KCL
(1) 定律内容。对于任一集总电路中的任一节点,在任一时刻,流进(或流出)该节点的所有支路电流的代数和为零;或对于任一集总电路中的任一节点,在任一时刻,流进该节点的所有支路电流的和等于流出该节点的所有支路电流的和。即如果 i݇(t)表示流入(或流出) 节点的电流,n 为节点处的支路数,有下面的式子成立:

(2) 定律的实质是电荷守恒。
(3) 关于 KCL 的说明有以下几点。
① KCL 是电荷守恒和电流连续性原理在电路中任意节点处的反映。
② KCL 是对节点处支路电流加的约束,与支路上的元件无关,与电路是线性还是非线性无关。
③ KCL 方程是按电流参考方向列写的,与电流实际方向无关。
④ KCL 可推广应用于电路中包围多个节点的任一闭合面——广义节点。
例如,图 1-30(a)中, i1+i2=i3或 i1+i2-i3=0;图 1-30(b)中,i1+i2+i3=0。

KVL
(1) 定律内容。对于任一集总电路中的任一回路,在任一时刻沿着该回路的所有支路 电压降的代数和为零;或对于任一集总电路中的任一回路节点,在任一时刻沿着该回路的 所有支路的电压降的和等于沿着该回路的所有支路的电压升的和。即如果 ( ) k v t 表示回路中 第 k 条支路电压,k 为回路中的支路数,有下面的式子成立

(2) 定律的实质是电荷守恒和能量守恒。
(3) 关于 KVL 的说明有以下几点。
① KVL 反映了电路遵从能量守恒。
② KVL 是对回路中的支路电压加的约束,与回路各支路上的元件无关,与电路是线性还是非线性无关。
③ 使用 KVL 时,直接用参考方向根据选定的绕行方向列写方程。
④ KVL 也适用于电路中任一假想的回路——广义回路。
例如在图 1-31 中,选择箭头所示的方向作为列写方程的绕行方向。对于 1、3、4 组成的 回路,有u1+u3-u4=0 。对于 1、2、4、5、7、8 组成的回路,有 u1-u2-u4+u7+u8-u5=0 。
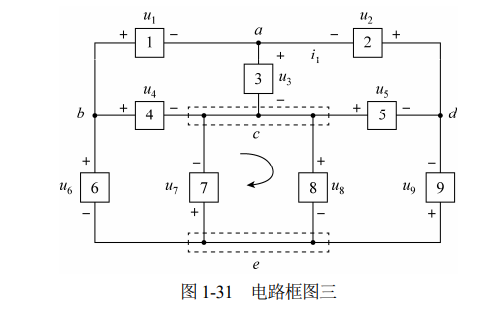
另外,注意列写 KVL 方程时使用双下标表示方法,在实际使用时常常用到两点间电压与路径无关的结论,例如对于图 1-31,有
![]()
KCL、KVL 小结
(1) KCL 是对支路电流的线性约束,KVL是对回路电压的线性约束。
(2) KCL、KVL 与组成支路的元件性质及参数无关。
(3) KCL 表明电荷在每一节点上是守恒的,KVL 是能量守恒的具体体现(电压与路径 无关)。
(4) 电路中 KCL、KVL 方程的独立性。
对于具有 n 个节点、b 条支路、m 个网孔的平面电路,独立的 KCL方程为 n −1 个,独 立的 KVL 方程为 m 个,其中 m = b − (n−1)。
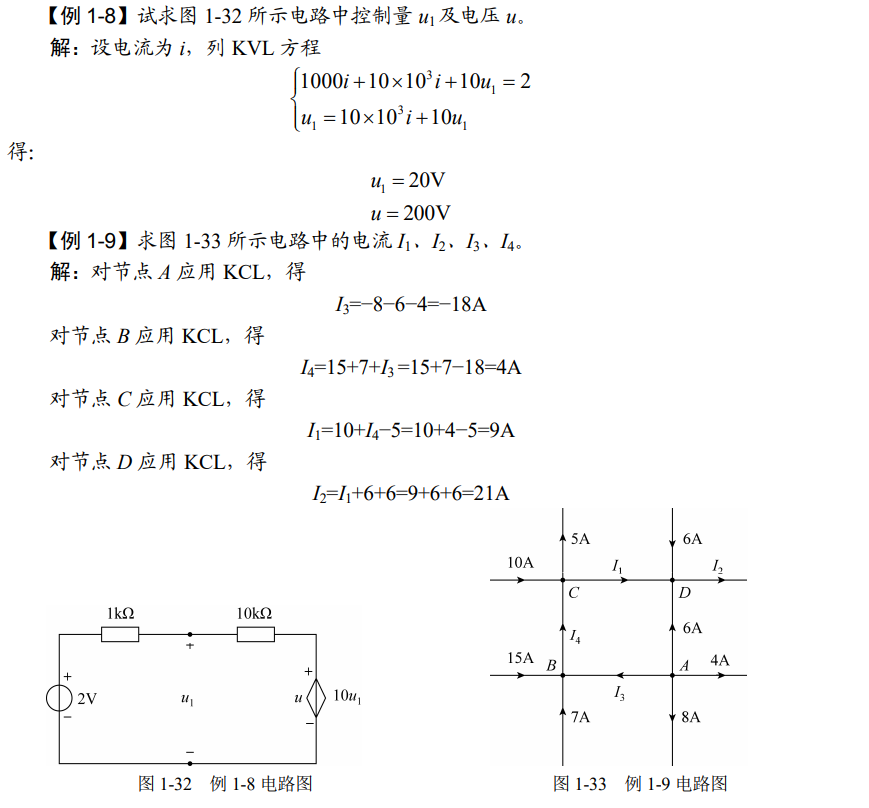
.