##队列部分-猫猫排队
是一种遵循先入先出规则的线性数据结构。
是一种模拟排队现象,新来的人不断加入到队列尾部,而位于队列头部的人不断离开。

##抽象数据类型队列的定义
队列是一种先进先出的线性表,它只允许在表的一端进行插入,而在另一端删除元素。
##图例显示
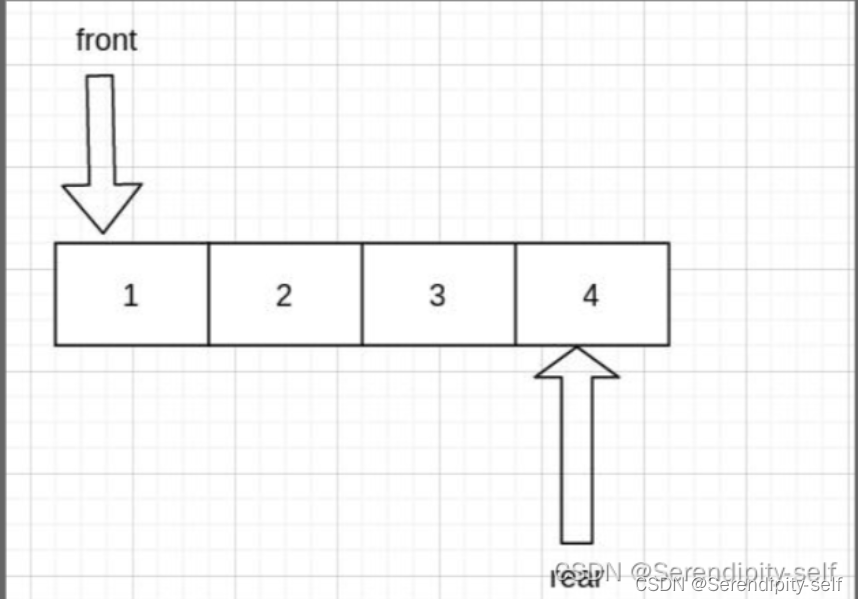
我们将队列头部称为“队首”,尾部称为“队尾”,将把元素加入队尾的操作称为“入队”,删除队首元素的操作称为“出队”。

##队列的常用操作
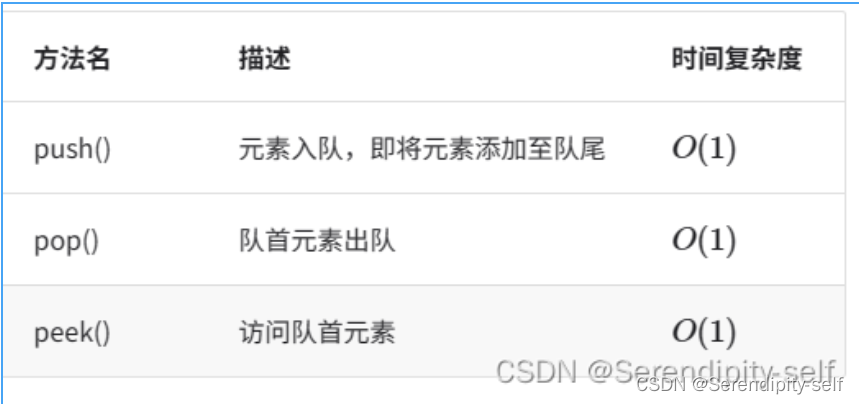
##图解
##基于数组的队列实现
我们在数组中进行删除首元素的时间复杂度为O(n),这就导致了出队的操作效率低下。
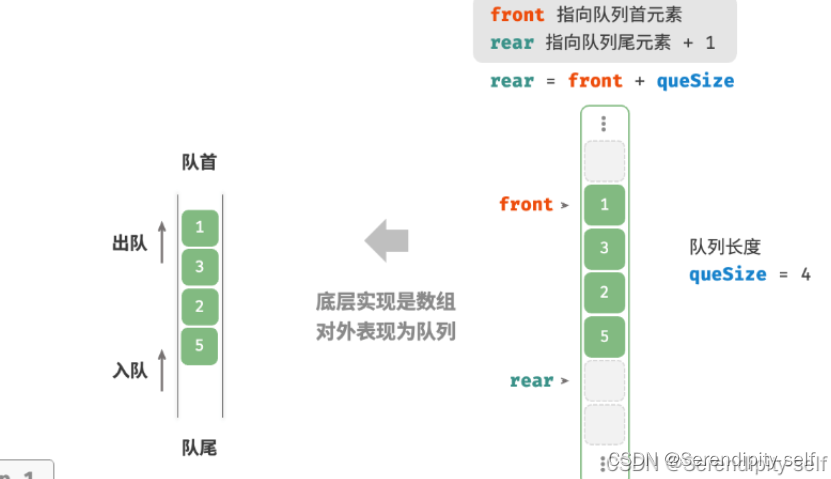
采用变量front指向队首元素的索引,rear = front + size ,通过一个变量size来记录队列的长度。
基于此设计,数组中所包含的元素的有效区间为[front,rear - 1]。
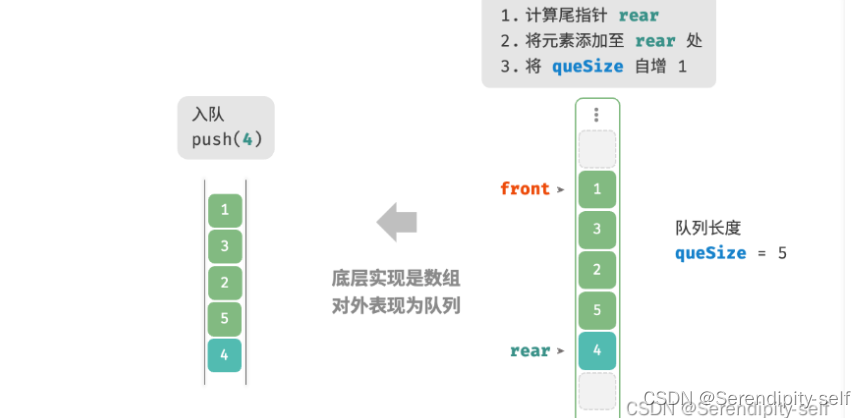
入队操作:只需要将元素赋值给rear索引处,并将size增加1。
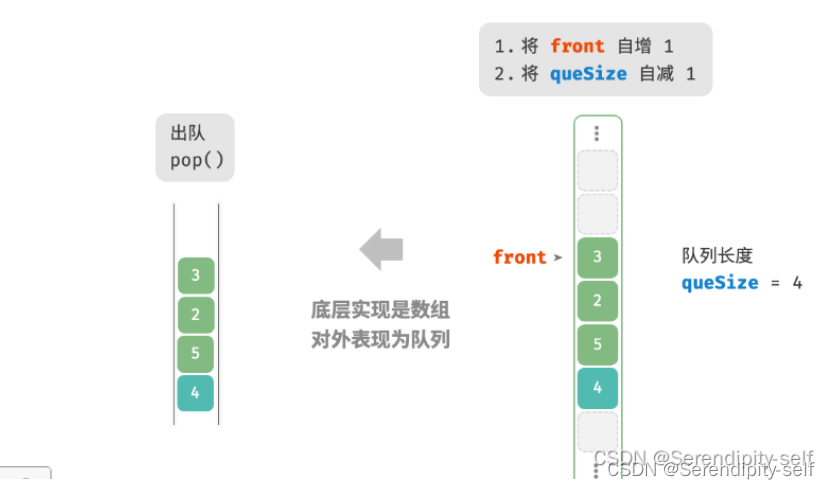
出队操作:只需要将front增加1,并将size减少1。
##问题:
在不断进行入队和出队的过程中,front 和 rear 都在向右移动,当它们到达数组尾部时就无法继续移动了。为了解决此问题,我们可以将数组视为首尾相接的“环形数组”。
对于环形数组,我们需要让 front 或 rear 在越过数组尾部时,直接回到数组头部继续遍历。这种周期性规律可以通过“取余操作”来实现,
##基于数组的队列代码实现
class ArrayQueue:
"""基于环形数组实现的队列"""
def __init__(self,size):
"""构造方法"""
self._nums : list[int] = [0] *size #用于存储队列元素的数组
self._front : int = 0 #队首指针,指向队首元素
self._size : int = 0 #队列长度
def capacity(self):
"""获取队列的容量"""
return len(self._nums)
def size(self):
"""获取队列的长度"""
return self._size
def is_empty(self):
"""判断队列是否为空"""
return self._size == 0
def push(self,num):
"""入队操作"""
if self._size == self.capacity():
raise IndexError("队列已满")
#计算尾指针,指向对尾的索引 + 1
#通过取余操作,实现rear超过数组尾部后回到头部
rear : int = (self._front + self._size) % self.capacity()
#将num添加至对尾
self._nums[rear] = num
self._size += 1
def pop(self):
"""出队"""
num : int = self.peek()
#队首指针指向后移动一位,若超过数组尾部后回到头部
rear : int = (self._front + self._size) % self.capacity()
self._size -= 1
return num
def peek(self):
"""访问队首元素"""
if self.is_empty():
raise IndexError("栈为空")
return self._nums[self._front]
def to_list(self):
"""转化成列表用于打印"""
res = [0] * self.size()
j : int = self._front
for i in range(self.size()):
res[i] = self._nums[(j%self.capacity())]
j += 1
return res时间效率:在基于数组的实现中,入对和出对操作都在预先分配好的连续内存中进行,具有很好的缓存本地性,因此效率较高。然而,如果入对时超出数组容量,会触发扩容机制,导致该次入对操作的时间复杂度变为O(n) 。
空间效率:在初始化列表时,系统会为列表分配“初始容量”,该容量可能超出实际需求;并且,扩容机制通常是按照特定倍率(例如 2 倍)进行扩容的,扩容后的容量也可能超出实际需求。因此,基于数组实现的栈可能造成一定的空间浪费。