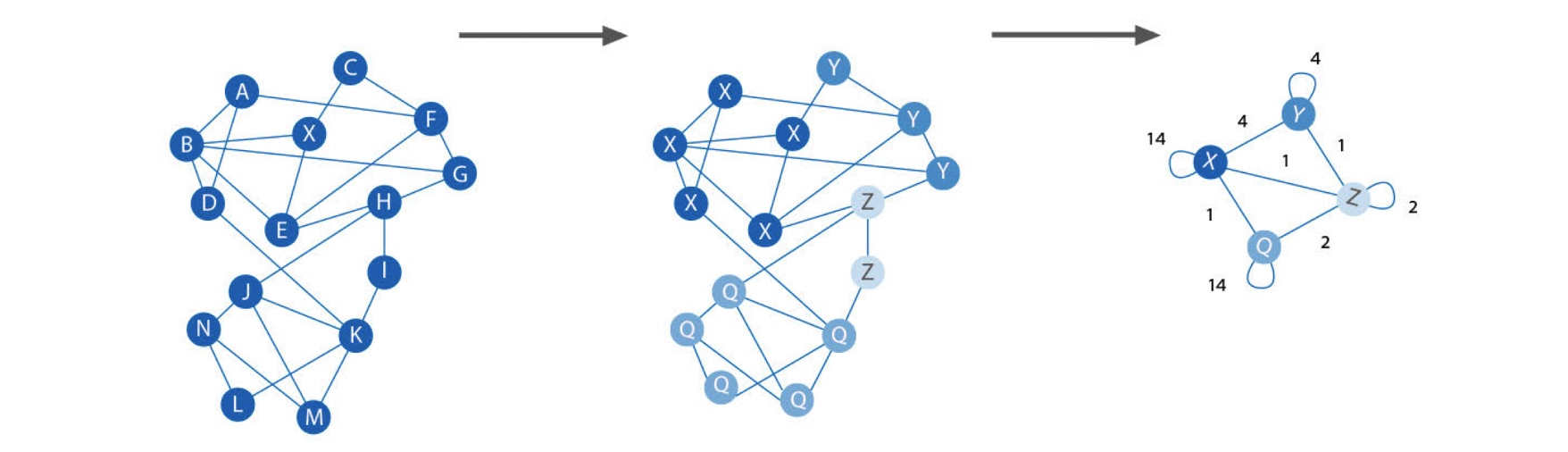
为什么要用图算法

图算法有助于我们理解关联数据。理解网络及其内部联系可以为洞察和创新提供不可思议的潜力。

图算法特别适用于理解结构和揭示高度关联的数据集中模式。目前，大数据汇集、混合和动态更新的需求非常强烈，图算法有助于体现数据的关联性和交互性，针对关系进行更复杂的分析，并可以为AI提供丰富的上下文信息。

随着数据间的联系越来越紧密，理解数据之间的依赖关系也就越来越重要。

路径查找算法

路径是图算法和图分析的基础，如：查找最短路径是使用图算法执行非常频繁的任务，最短路径是跳数最少或权重最小的遍历路径。如果图是有向的，它就是指两个节点之间关系方向所允许的最短路径。

广度优先搜索算法

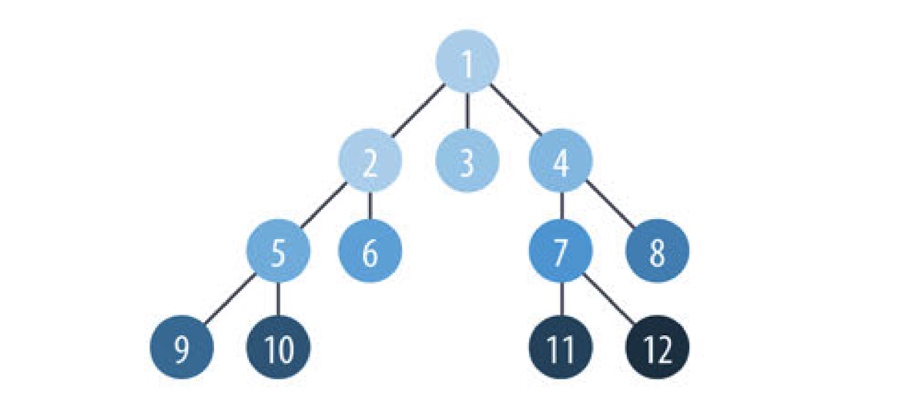
首先访问最邻近的节点

深度优先搜索算法

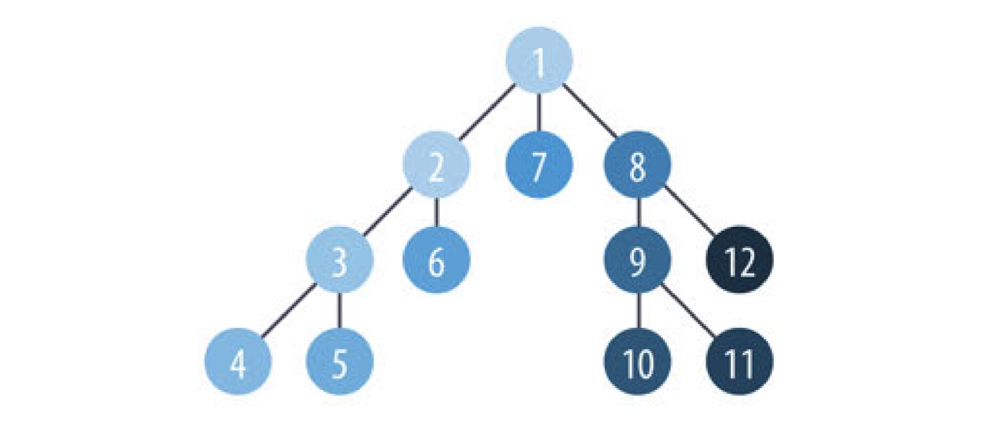
先沿着各分支进行搜索

最短路径算法

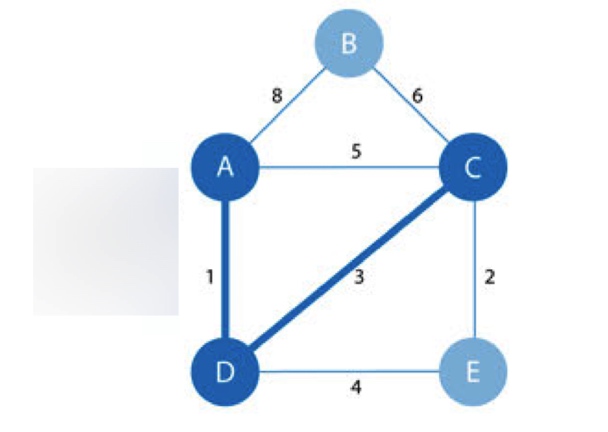
所有点对最短路径算法

单源最短路径算法

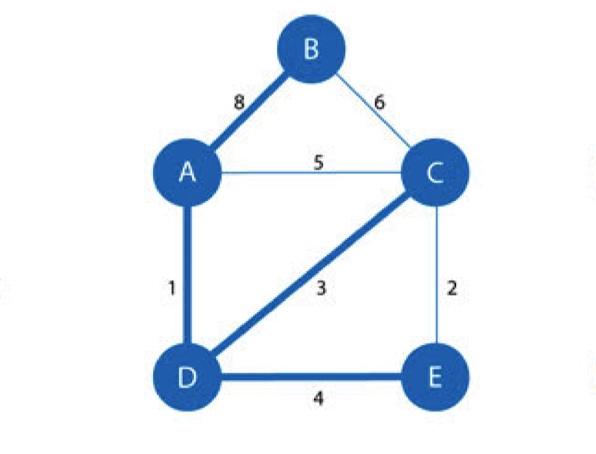
最小生成树算法

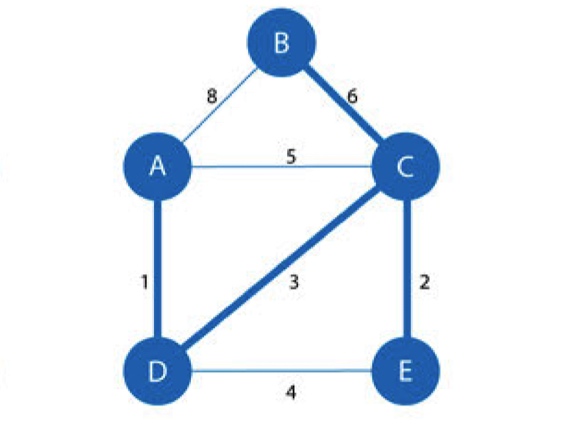
随机游走算法

中心性算法

中心性的要点就是了解网络中哪个节点更重要，什么是“重要”，因此我们需要创建不同类型的中心性算法来满足不同场景下的需求。

度中心性算法

度中心性算法计算节点的输入关系数和输出关系数，查找图中受欢迎的节点。节点的度是节点拥有的直接关系数，可按入度和出度两种指标计算。

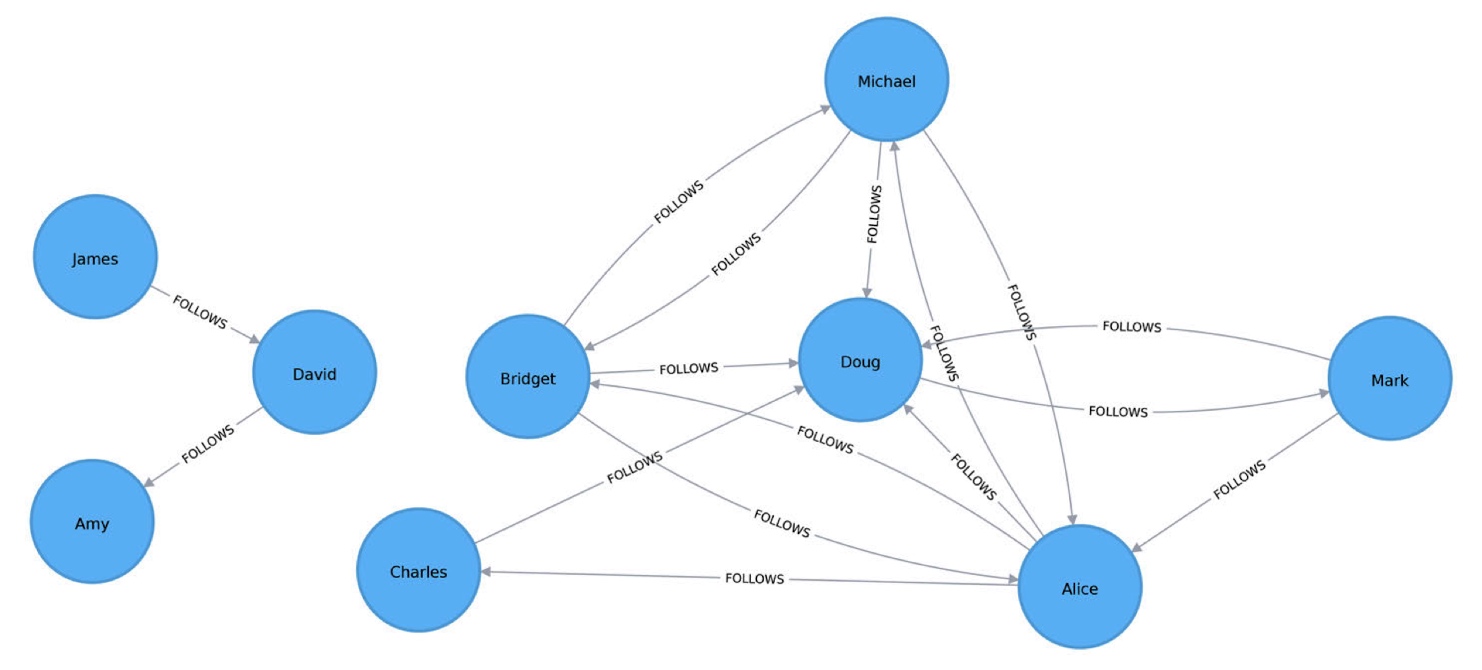
度中心性的可视化

接近中心性算法

中间中心性算法

中间中心性算法检测节点对图中信息流或资源的影响程度，通常用于查找将图的一部分与另一部分桥接的节点。

中间中心性算法计算连通图中每对节点之间的最短（加权）路径。每个节点的分值根据通过该点的最短路径数量确定。通过节点的最短路径数量越多，其得分就越高。

在某些场景下，最关键的要素并不是拥有绝对权威的或最高地位的要素。而某些中间人将各个群体联系起来，或者说中间人对资源或信息流的控制权最大。

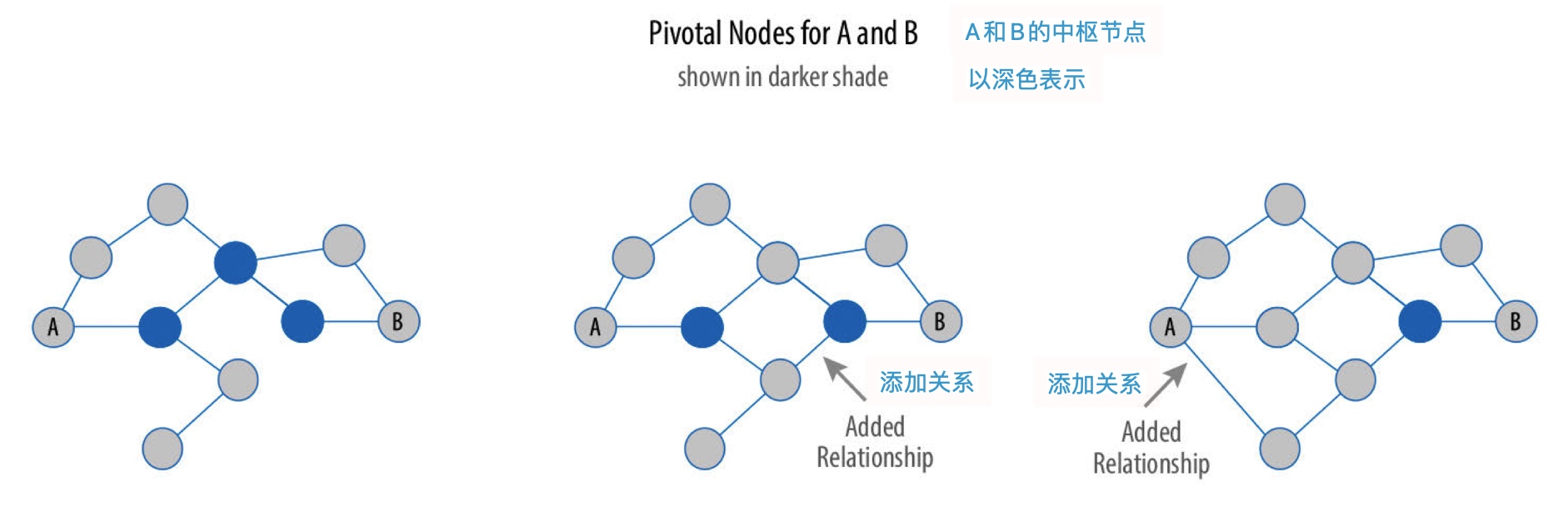
中枢节点位于两个节点之间的每条最短路径上。创建更多最短路径可以减少中心节点的数量，可用于降低风险等场景。

PageRank算法

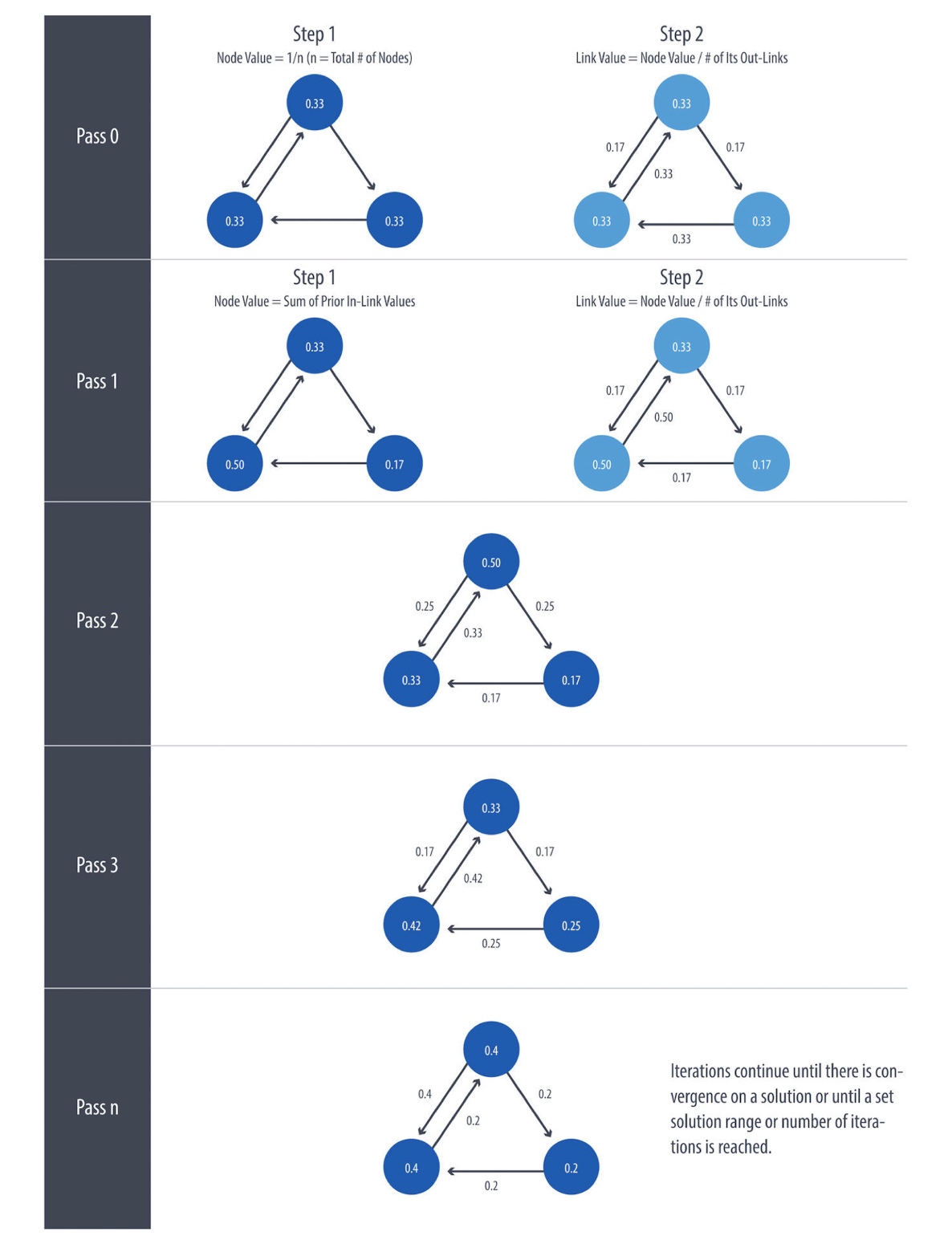
PageRank算法可能是最著名的中心性算法，用来度量节点的传递性（或方向性）影响。

PageRank算法是以Google联合创始人Larry Page的姓氏命名的，Larry Page创建PageRank算法的初衷是在谷歌搜索结果中对网站进行评级。其基本假设是： 一个网页如果有更多或更有影响力的输入链接，就更有可能是可信来源。PageRank算法度量节点输入关系的数量和质量，以此估计该节点的重要性。 在网络中，如果节点拥有的来自其他有影响力的节点的输入关系越多，那么它就越有可能在网络中占据主导地位。

前面几种中心性算法都是度量节点的直接影响，PageRank算法则考虑节点的邻近点影响，及其临节点的邻节点的影响。例如：

1

与拥有一大堆影响力小的朋友相比，拥有几个很有影响力的朋友能让人更有影响力。

PageRank算法的计算方法有两种：

1. 将一个节点的等级迭代分散到其邻节点。
2. 随机遍历图并计算每个节点在遍历过程中被名中的频率。

社团发现算法

连通性是图论的核心概念之一，它支持复杂网络分析，如：社团发现。现实世界中的大多数网络或多或少呈现出独立子图这样的子结构。识别社团对于评价群体行为和突发现象有不可或缺的作用。

识别社团的一般原则: 社团成员在群组内部的关系要多于其与群组外部节点的关系。识别这些有关联关系的集合可以揭示节点簇、孤立群组和网络结构。

连通度用于发现社团并量化分组的质量。评估图中不同类型的社团有助于揭示图的结构，如：中心结构和层级结构，也有助于了解某个群组和吸引和排斥其他群组的倾向。

度量算法（面向整体关系稠密度，用于衡量图的结构特性）

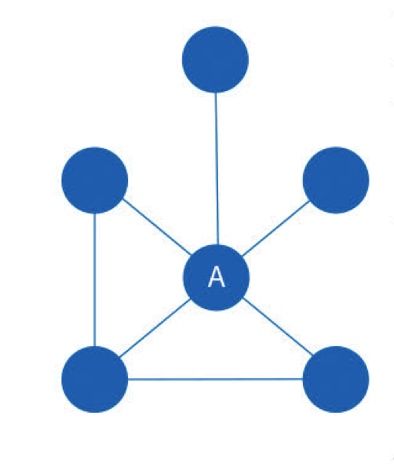
三角形计数算法

三角计数算法（Triangle Count）统计图中三角形个数。三角形越多，代表图中节点关联程度越高，组织关系越严密。

聚类系数分量

聚类系数表示一个图中节点聚集程度的系数。在现实的网络中，尤其是在特定的网络中，由于相对高密度连接点的关系，节点总是趋向于建立一组严密的组织关系。聚类系数算法（Cluster Coeffcient）用于计算图中节点的聚集程度。

分量算法（用于发现连通簇）

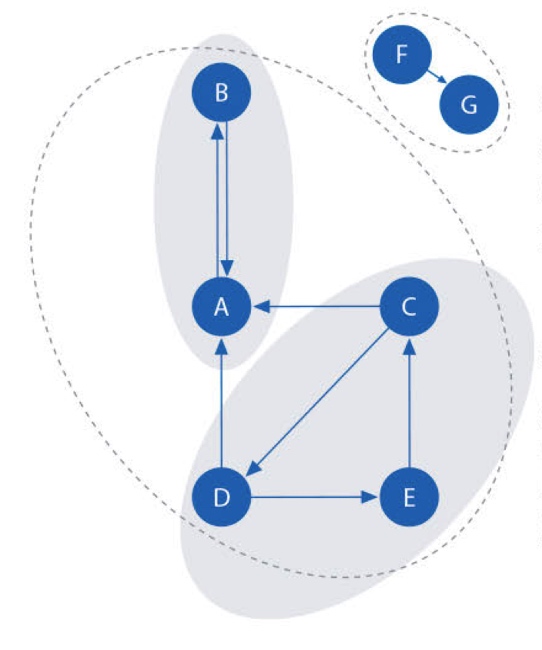
强连通分量算法

在如上有向图中，如果两个顶点A、B间，有一条从B到A的有向路径，同时还有一条从A到B的有向路径，则称A、B两个顶点强连通。

如果有向图中的每两个顶点都强连通，称该有向图是一个强连通图。有向非强连通图的极大强连通子图，称为强连通分量。

连通分量算法

标签传播算法（可基于节点标签快速推断群组）

标签传播算发是一种基于图的半监督学习方法，基本思路是用已标记节点的标签信息去预测未标记节点的标签信息。基本过程如下：

1. 为每个节点随机的指定一个自己特有的标签；
2. 逐轮刷新所有节点的标签，直到所有节点的标签不再发生变化为止。对于每一轮刷新，节点标签的刷新规则如下：

对于某一个节点，考察其所有邻居节点的标签，并进行统计，将出现个数最多的那个标签赋值给当前节点。当个数最多的标签不唯一时，随机选择一个标签赋值给当前节点。

在标签传播算法中，节点的标签更新通常有同步更新和异步更新两种方法。同步更新是指，节点x在t时刻的更新是基于邻接节点在t-1时刻的标签。异步更新是指，节点x在t时刻更新时，其部分邻接节点是t时刻更新的标签，还有部分的邻接节点是t-1时刻更新的标签。LPA算法在标签传播过程中采用的是同步更新，研究者们发现同步更新应用在二分结构网络中，容易出现标签震荡的现象。因此，之后的研究者大多采用异步更新策略来避免这种现象的出现。

Louvain模块度算法（用于研究分组的质量和层级结构）