647. Palindromic Substrings
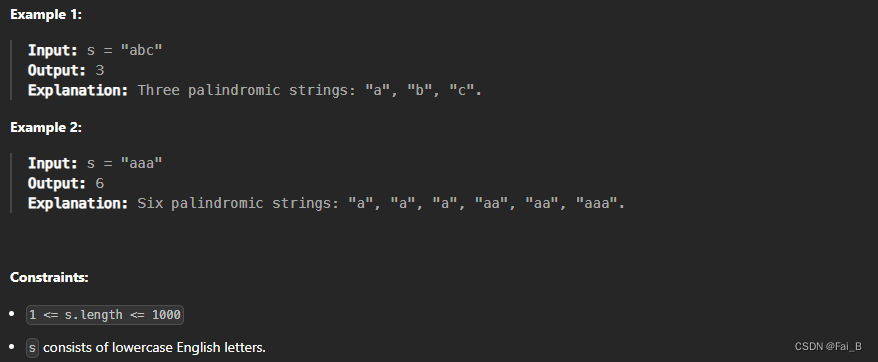
Given a string s, return the number of palindromic substrings 回文子串 in it.
A string is a palindrome when it reads the same backward as forward.
A substring is a contiguous sequence of characters within the string.
nomal:
Time complexity: O(n^2)
Space complexity: O(1)
class Solution:
def countSubstrings(self, s: str) -> int:
count = 0
for left in range(len(s)):
for right in range(left, len(s)):
if s[left : right + 1] == s[left : right + 1][::-1]: # wrong:[-1]最后一个字符
count += 1
return count
DP:
Time complexity: O(n^2)
Space complexity: O(n^2)
class Solution:
def countSubstrings(self, s: str) -> int:
dp = [[False] * len(s) for _ in range(len(s))]
result = 0
for i in range(len(s)-1, -1, -1): #注意遍历顺序
for j in range(i, len(s)):
if s[i] == s[j]:
if j - i <= 1: #情况一 和 情况二
result += 1
dp[i][j] = True
elif dp[i+1][j-1]: #情况三
result += 1
dp[i][j] = True
return result2 pointer:
Determining the palindrome string is a matter of finding the center and then spreading it out to both sides to see if it is symmetrical.
When traversing the central point, it is important to note that there are two cases of central points.
One element can be used as the center point, and two elements can be used as the center point.
Time complexity: O(n^2)
Space complexity: O(1)
class Solution:
def countSubstrings(self, s: str) -> int:
result = 0
for i in range(len(s)):
result += self.extend(s, i, i, len(s)) #以i为中心
result += self.extend(s, i, i+1, len(s)) #以i和i+1为中心
return result
def extend(self, s, i, j, n):
res = 0
while i >= 0 and j < n and s[i] == s[j]:
i -= 1
j += 1
res += 1
return res516. Longest Palindromic Subsequence
Given a string s, find the longest palindromic subsequence回文子序列's length in s.
A subsequence is a sequence that can be derived衍生 from another sequence by deleting some or no elements without changing the order of the remaining elements.

1. dp[i][j]: the length of the longest palindrome subsequence of the string s in the range [i, j] is dp[i][j].
2. If s[i] is the same as s[j]: then dp[i][j] = dp[i + 1][j - 1] + 2;
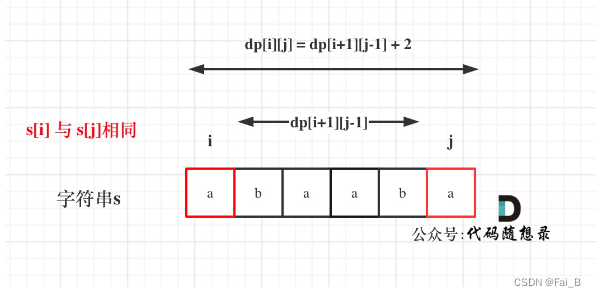
3. If s[i] is not the same as s[j]: then dp[i][j] must be taken to be maximal,
dp[i][j] = max(dp[i + 1][j], dp[i][j - 1]);
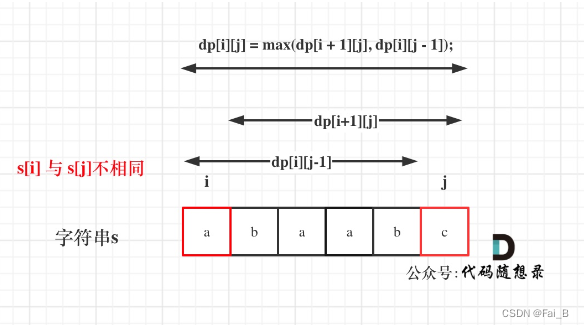
4. Determine the traversal order
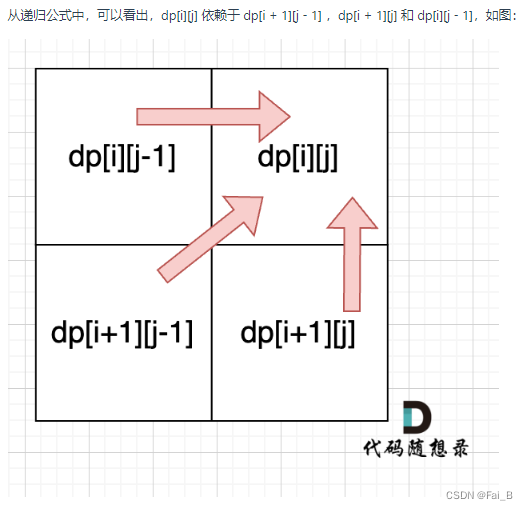
5. initial
for i in range(len(s)):
dp[i][i] == 1
6. return
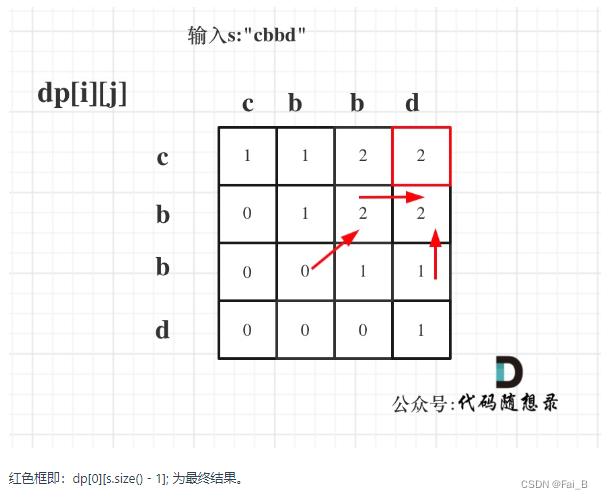
DP:
Time complexity: O(n^2)
Space complexity: O(n^2)
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
dp = [[0] * len(s) for _ in range(len(s))]
for i in range(len(s)):
dp[i][i] = 1
for i in range(len(s)-1, -1, -1):
for j in range(i+1, len(s)):
if s[i] == s[j]:
dp[i][j] = dp[i+1][j-1] + 2
else:
dp[i][j] = max(dp[i+1][j], dp[i][j-1])
return dp[0][-1]dfs:
class Solution:
def longestPalindromeSubseq(self, s: str) -> int:
n = len(s)
# 使用记忆化搜索实现
@cache
def dfs(i, j):
if i > j:
return 0
if i == j:
return 1
if s[i] == s[j]:
return dfs(i + 1, j - 1) + 2
else:
return max(dfs(i + 1, j), dfs(i, j - 1))
return dfs(0, n - 1)