系列文章目录
CasADi - 最优控制开源 Python/MATLAB 库
文章目录
- 系列文章目录
- 前言
- 一、机器人硬件对比
- 1.1 Teensy 上的微控制器基准测试
- 1.2 机器人硬件
- 1.3 BibTeX
- 二、求解器
- 三、功能(预期)
- 3.1 高效
- 3.2 鲁棒
- 3.3 可嵌入式
- 3.4 最小依赖性
- 3.5 高效热启动
- 3.6 接口
- 四、在 Ubuntu 安装
- 4.1 在终端克隆此 repo
- 4.2 导航至根目录并运行
- 4.3 执行 CMake 配置步骤
- 4.4 构建 TinyMPC
- 五、示例
- 5.1 运行四旋翼飞行器悬停示例
- 5.2 运行 codegen 示例,然后在该目录下按照相同的构建步骤进行操作
前言
TinyMPC: 资源受限微控制器上的模型预测控制
作者:Anoushka Alavilli*, Khai Nguyen*, Sam Schoedel*, Brian Plancher, Zachary Manchester
Carnegie Mellon University, Barnard College
模型预测控制(Model-predictive control,MPC)是控制受复杂约束条件(complex constraints)影响的高动态机器人系统(highly dynamic robotic systems)的有力工具。然而,MPC 的计算要求很高,在资源有限的小型机器人平台上实施往往不切实际。我们推出的 TinyMPC 是一种高速 MPC 求解器,内存占用少,适用于小型机器人上常见的微控制器。我们的方法基于交替方向乘子法(ADMM),并利用 MPC 问题的结构来提高效率。我们以最先进的求解器 OSQP 为基准,对 TinyMPC 进行了演示,速度提高了近一个数量级,同时还在一个重达 27 克的四旋翼机器人上进行了硬件实验,演示了高速轨迹跟踪(high-speed trajectory tracking)和动态避障(dynamic obstacle avoidance)。
一、机器人硬件对比
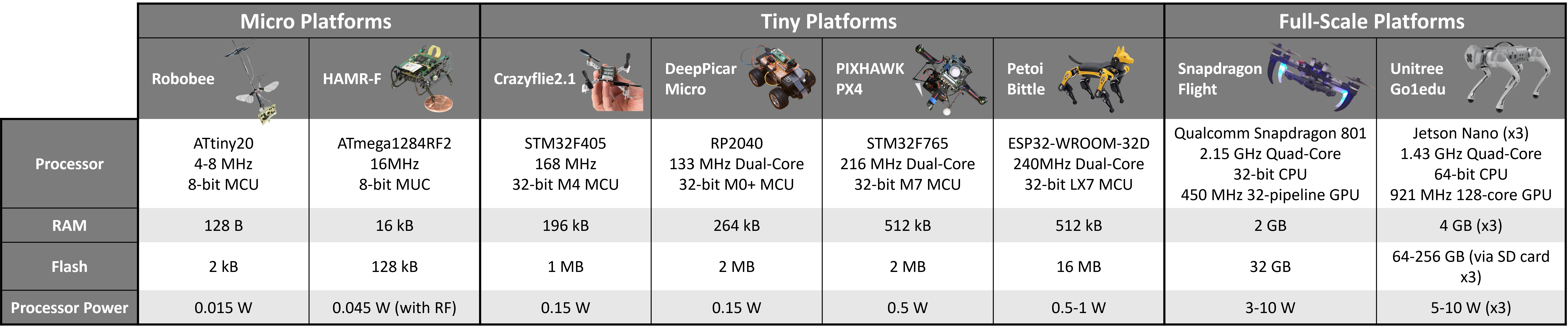

1.1 Teensy 上的微控制器基准测试
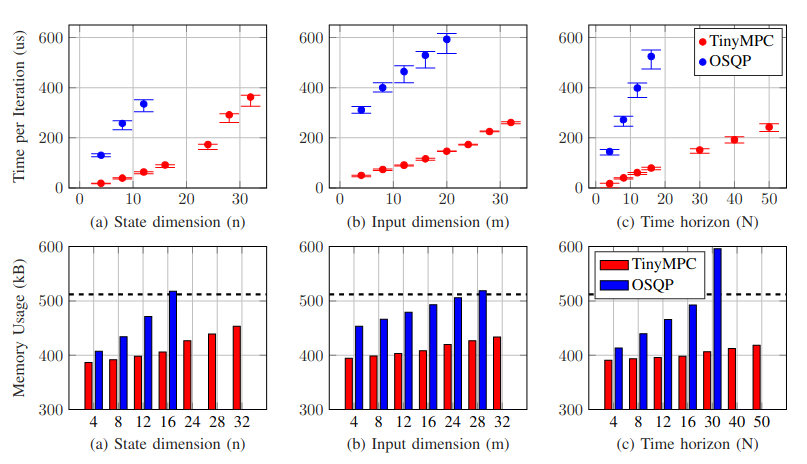
1.2 机器人硬件

1.3 BibTeX
@misc{tinympc,
title={TinyMPC: Model-Predictive Control on Resource-Constrained Microcontrollers},
author={Anoushka Alavilli and Khai Nguyen and Sam Schoedel and Brian Plancher and Zachary Manchester},
year={2023},
eprint={2310.16985},
archivePrefix={arXiv},
primaryClass={cs.RO}
}
二、求解器
TinyMPC 求解器是一个数值优化软件包,用于求解默认形式的凸二次规划型模型预测控制(convex quadratic model-predictive control)
minimize:
1
2
(
x
N
−
x
ˉ
N
)
T
Q
f
(
x
N
−
x
ˉ
N
)
+
∑
k
=
0
N
(
1
2
(
x
k
−
x
ˉ
k
)
T
Q
(
x
k
−
x
ˉ
k
)
+
1
2
(
u
k
−
u
ˉ
k
)
T
R
(
u
k
−
u
ˉ
k
)
)
subject to:
x
k
+
1
=
A
x
k
+
B
u
k
u
‾
≤
u
k
≤
u
‾
x
‾
≤
x
k
≤
x
‾
\begin{array}{l l}{\operatorname*{minimize:}}&{\dfrac{1}{2}(x_{N}-\bar{x}_{N})^{T}Q_{f}(x_{N}-\bar{x}_{N})+{{\sum_{k=0}^{N}\bigl(\frac{1}{2}(x_{k}-\bar{x}_{k})^{T}Q(x_{k}-\bar{x}_{k})+\frac{1}{2}\bigl(u_{k}-\bar{u}_{k}\bigr)^{T}R(u_{k}-\bar{u}_{k})\bigr)}}} \\ {\operatorname*{subject\;to:}}&x_{k+1}=A x_{k}+B u_{k} \\ & \overline{{{u}}}\,\leq\,u_{k}\,\leq\underline{{u}} \\ & \overline{{{x}}}\,\leq\,x_{k}\,\leq\underline{{x}} \end{array}
minimize:subjectto:21(xN−xˉN)TQf(xN−xˉN)+∑k=0N(21(xk−xˉk)TQ(xk−xˉk)+21(uk−uˉk)TR(uk−uˉk))xk+1=Axk+Buku≤uk≤ux≤xk≤x
其中, x k ∈ R n x_{k}\in\mathbb{R}^{n} xk∈Rn、 u k ∈ R m u_{k}\in\mathbb{R}^{m} uk∈Rm 分别为时间步长为 k 时的状态和控制输入,N 为时间步长(也称为视平线), A ∈ R n × n A\in\mathbb{R}^{n\times n} A∈Rn×n 和 B ∈ R n × m B\in\mathbb{R}^{n\times m} B∈Rn×m 定义了系统动力学, Q ≥ 0 Q\geq0 Q≥0、 R ≻ 0 R\succ0 R≻0 和 Q f ≥ 0 Q_{f}\geq0 Qf≥0 为对称成本权重矩阵, x ~ k {\tilde{x}}_{k} x~k 和 u ˉ k {\bar{u}}_{k} uˉk 是状态和输入参考轨迹。
三、功能(预期)
3.1 高效
它采用基于 ADMM 的定制一阶方法,无需矩阵因式分解。所有其他操作都非常简单。它还利用 MPC 问题中的结构,为基元更新实现了黎卡提递归(Riccati recursion)。
3.2 鲁棒
该算法完全 free,而且不需要对问题数据做任何假设(问题只需要是凸的)。它就是这么简单!
3.3 可嵌入式
它有一个简单的接口,无需内存管理器即可生成定制的可嵌入 C 代码。
3.4 最小依赖性
它只需要 Eigen 就能运行。
3.5 高效热启动
它可以轻松热启动,并且可以缓存矩阵因式分解,从而极其高效地解决参数化问题。
3.6 接口
它为 C、C++、Julia、Matlab 和 Python 提供了接口。
四、在 Ubuntu 安装
4.1 在终端克隆此 repo
git clone git@github.com:TinyMPC/TinyMPC.git
4.2 导航至根目录并运行
cd TinyMPC
mkdir build && cd build
4.3 执行 CMake 配置步骤
cmake ../
4.4 构建 TinyMPC
make
五、示例
5.1 运行四旋翼飞行器悬停示例
./examples/example_quadrotor_hovering
tracking error at step 0: 2.2472
tracking error at step 1: 2.9549
tracking error at step 2: 2.5478
tracking error at step 3: 2.6331
tracking error at step 4: 3.1375
tracking error at step 5: 3.6413
tracking error at step 6: 4.0214
tracking error at step 7: 4.2898
tracking error at step 8: 4.5070
tracking error at step 9: 4.6282
tracking error at step 10: 4.3689
tracking error at step 11: 3.8895
tracking error at step 12: 3.3699
tracking error at step 13: 2.8681
tracking error at step 14: 2.3877
tracking error at step 15: 1.9336
tracking error at step 16: 1.5516
tracking error at step 17: 1.2588
tracking error at step 18: 1.0420
tracking error at step 19: 0.8844
tracking error at step 20: 0.7680
tracking error at step 21: 0.6773
tracking error at step 22: 0.6009
tracking error at step 23: 0.5316
tracking error at step 24: 0.4658
tracking error at step 25: 0.4024
tracking error at step 26: 0.3416
tracking error at step 27: 0.2839
tracking error at step 28: 0.2305
tracking error at step 29: 0.1822
tracking error at step 30: 0.1393
tracking error at step 31: 0.1023
tracking error at step 32: 0.0715
tracking error at step 33: 0.0472
tracking error at step 34: 0.0301
tracking error at step 35: 0.0217
tracking error at step 36: 0.0218
tracking error at step 37: 0.0251
tracking error at step 38: 0.0279
tracking error at step 39: 0.0291
tracking error at step 40: 0.0290
tracking error at step 41: 0.0277
tracking error at step 42: 0.0254
tracking error at step 43: 0.0227
tracking error at step 44: 0.0197
tracking error at step 45: 0.0167
tracking error at step 46: 0.0140
tracking error at step 47: 0.0116
tracking error at step 48: 0.0097
tracking error at step 49: 0.0082
tracking error at step 50: 0.0072
tracking error at step 51: 0.0067
tracking error at step 52: 0.0065
tracking error at step 53: 0.0065
tracking error at step 54: 0.0065
tracking error at step 55: 0.0064
tracking error at step 56: 0.0063
tracking error at step 57: 0.0062
tracking error at step 58: 0.0061
tracking error at step 59: 0.0059
tracking error at step 60: 0.0058
tracking error at step 61: 0.0056
tracking error at step 62: 0.0055
tracking error at step 63: 0.0054
tracking error at step 64: 0.0053
tracking error at step 65: 0.0052
tracking error at step 66: 0.0052
tracking error at step 67: 0.0052
tracking error at step 68: 0.0052
tracking error at step 69: 0.0052
5.2 运行 codegen 示例,然后在该目录下按照相同的构建步骤进行操作
./examples/example_codegen
A = [1, 1]
[5, 2]
B = [3, 4]
[3, 1]
Q = [1.1, 0]
[ 0, 1.1]
R = [2.1, 0]
[ 0, 2.1]
rho = 0.1
Kinf converged after 5 iterations
Precomputing finished
Kinf = [ 1.36, 0.5335]
[-0.6323, -0.1066]
Pinf = [8.899, 2.664]
[2.664, 2.046]
Quu_inv = [ 0.1076, -0.09799]
[-0.09799, 0.09522]
AmBKt = [-0.5502, 1.553]
[-0.1739, 0.5062]
coeff_d2p = [7.438e-06, 8.381e-06]
[2.127e-06, 2.398e-06]
Creating generated code directory at /home/khai/SSD/Code/TinyMPC/generated_code
ERROR OPENING DATA WORKSPACE FILE
Segmentation fault