系列文章目录

---

---

前言

---

一、如何评估拟合优度

用一个或多个模型拟合数据后，您应该评估拟合的好坏。第一步应该是目测 "曲线拟合器 "应用程序中显示的拟合曲线。除此之外，工具箱还提供了这些方法来评估线性和非线性参数拟合的拟合优度：

• 拟合优度统计

• 残差分析

• 置信度和预测边界

正如统计文献中常见的那样，"拟合优度 "一词在这里有多种含义： 一个 "拟合良好 "的模型可能是

• 根据最小二乘法拟合的假设，您的数据可以合理地来自该模型

• 模型系数的估计不确定性很小

• 能解释数据中很大一部分变异性，并能很有把握地预测新的观测结果。

特定应用可能还要求模型拟合的其他方面，这些方面对于实现良好拟合也很重要，例如一个易于解释的简单模型。本文介绍的方法可以帮助您确定所有这些意义上的拟合优度。

这些方法分为两类：图解法和数值法。绘制残差和预测边界是图形方法，有助于直观解释，而计算拟合优度统计量和系数置信区间则是数字方法，有助于统计推理。

一般来说，图形测量比数值测量更有优势，因为图形测量可以让您一次性查看整个数据集，而且可以轻松显示模型与数据之间的各种关系。而数值度量则更多地关注数据的某一特定方面，通常会试图将这些信息压缩成一个单一的数字。实际上，根据您的数据和分析要求，您可能需要使用这两种类型来确定最佳拟合。

请注意，根据这些方法，可能没有一种拟合适合您的数据。在这种情况下，您可能需要选择不同的模型。也有可能所有的拟合优度都表明某个拟合模型是合适的。但是，如果您的目标是提取具有物理意义的拟合系数，但您的模型并不能反映数据的物理特性，那么得出的系数就毫无用处。在这种情况下，了解数据代表什么以及如何测量数据与评估拟合度同样重要。

二、拟合优度统计

使用图形方法评估拟合优度后，应检查拟合优度统计量。曲线拟合工具箱™ 软件支持参数模型的拟合优度统计：

• 误差平方和 (SSE)

• R 平方

• 误差自由度 (DFE)

• 调整后的 R 平方

• 均方根误差 (RMSE)

对于当前拟合，这些统计信息会显示在曲线拟合器应用程序的 "结果 "窗格中。对于当前曲线拟合会话中的所有拟合，可以在 "拟合表 "窗格中比较拟合优度统计量。

要在命令行下检查拟合优度统计，可以选择

• 在曲线拟合器应用程序中，将拟合结果和拟合优度导出至工作区。在 "曲线拟合器 "选项卡的 "导出 "部分，单击 "导出 "并选择 “导出到工作区”。

• 使用拟合函数指定 gof 输出参数。

2.1 SSE - 误差引起的平方和

该统计量用于衡量响应值与拟合响应值的总偏差。也称为残差平方和，通常标记为 SSE。
$$SSE=\sum _{i=1}^n{w}_i(y_i-{\hat{y}}_i{)}^2$$

数值越接近 0，表明模型的随机误差成分越小，拟合结果对预测越有用。

2.2 R 平方

该统计量衡量拟合在解释数据变化方面的成功程度。换一种说法，R 平方是响应值与预测响应值之间相关性的平方。它也被称为多重相关系数的平方和多重决定系数。

R 平方定义为回归平方和（SSR）与总平方和（SST）之比。SSR 的定义是
$$SSR=\sum _{i=1}^n{w}_i({\hat{y}}_i-\bar{y}{)}^2$$

SST 也称为均值平方和，其定义为

$$SST=\sum _{i=1}^n{w}_i(y_i-\overline{y}{)}^2$$

其中，SST = SSR + SSE。根据这些定义，R 方表示为
$$\mathrm{R}-\mathrm{square}=\frac{SSR}{SST}=1-\frac{SSE}{SST}$$

R-square 的值可以在 0 和 1 之间任意取值，值越接近 1，说明模型解释的变异比例越大。例如，R 平方值为 0.8234 意味着拟合解释了平均值数据总变异的 82.34%。

如果增加模型中拟合系数的数量，虽然拟合效果在实际意义上可能没有改善，但 R 平方却会增加。为了避免这种情况，您应该使用下面描述的自由度调整 R 平方统计量。

请注意，对于不包含常数项的方程，R 平方有可能为负值。因为 R 平方被定义为拟合所解释的方差比例，如果拟合实际上比仅仅拟合一条水平线更差，那么 R 平方就是负值。在这种情况下，R 平方不能解释为相关性的平方。这种情况表明模型中应加入常数项。

2.3 自由度调整 R 平方

该统计量使用上文定义的 R 平方统计量，并根据残差自由度对其进行调整。残差自由度的定义是响应值 n 的数量减去根据响应值估计的拟合系数 m 的数量。
$$\nu =n-m$$

v 表示计算平方和所需的涉及 n 个数据点的独立信息的数量。请注意，如果参数是有界的，且一个或多个估计值处于其边界，则这些估计值被视为固定值。自由度随此类参数的数量而增加。

当比较两个嵌套模型时，调整后的 R 平方统计量通常是拟合质量的最佳指标。
$$\mathrm{adjusted}\mathrm{R}-\mathrm{square}=1-\frac{SSE(n-1)}{SST(\nu )}$$

调整后的 R 平方统计量可以是小于或等于 1 的任何数值，数值越接近 1 表示拟合度越高。当模型中包含的项无助于预测响应时，就会出现负值。

2.4 均方根误差

该统计量也称为拟合标准误差和回归标准误差。它是对数据中随机成分的标准偏差的估计，定义为
$$RMSE=s=\sqrt{MSE}$$

其中，MSE 是均方误差或残差均方
$$MSE=\frac{SSE}{\nu }$$

与 SSE 一样，MSE 值接近 0 表示拟合结果更有利于预测。

三、MATLAB - 评估曲线拟合度

本示例展示了如何进行曲线拟合。

3.1 加载数据并拟合多项式曲线

load census
curvefit = fit(cdate,pop,'poly3','normalize','on')

curvefit = 
     Linear model Poly3:
     curvefit(x) = p1*x^3 + p2*x^2 + p3*x + p4
       where x is normalized by mean 1890 and std 62.05
     Coefficients (with 95% confidence bounds):
       p1 =       0.921  (-0.9743, 2.816)
       p2 =       25.18  (23.57, 26.79)
       p3 =       73.86  (70.33, 77.39)
       p4 =       61.74  (59.69, 63.8)

输出结果显示拟合模型方程、拟合系数以及拟合系数的置信区间。

3.2 绘制拟合方程、数据、残差和预测范围图

plot(curvefit,cdate,pop)

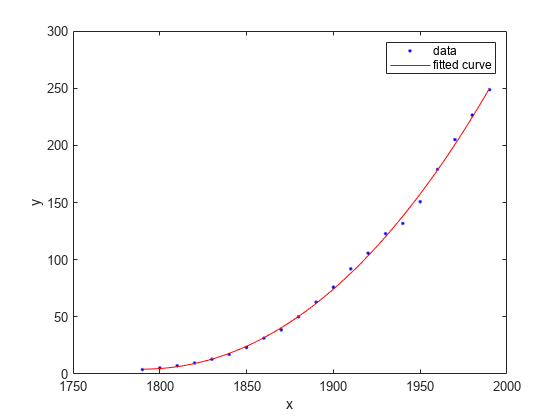
绘制残差拟合图。

plot(curvefit,cdate,pop,'Residuals')

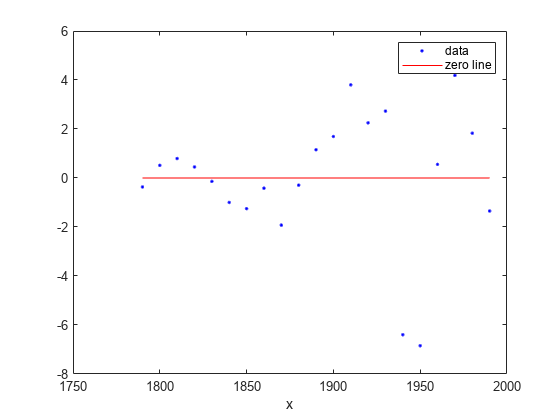
绘制拟合预测范围图。

plot(curvefit,cdate,pop,'predfunc')

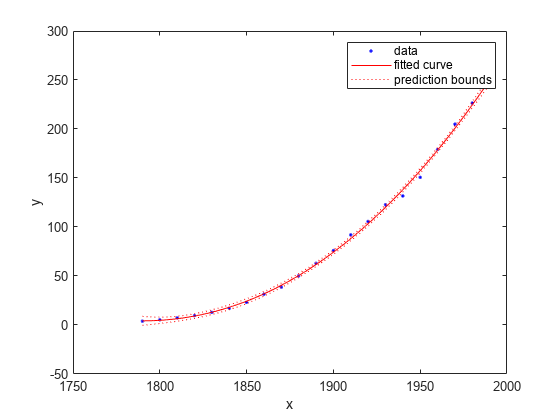
3.3 评估指定点3的拟合效果

通过指定一个 x 值，在一个特定点上评估拟合结果，使用下面的表格：y = fittedmodel(x)。

curvefit(1991)

ans = 252.6690

3.4 评估多点拟合值

评估模型的矢量值，以推断 2050 年的情况。

xi = (2000:10:2050).';
curvefit(xi)

ans = 6×1

  276.9632
  305.4420
  335.5066
  367.1802
  400.4859
  435.4468

获取这些值的预测范围。

ci = predint(curvefit,xi)

ci = 6×2

  267.8589  286.0674
  294.3070  316.5770
  321.5924  349.4208
  349.7275  384.6329
  378.7255  422.2462
  408.5919  462.3017

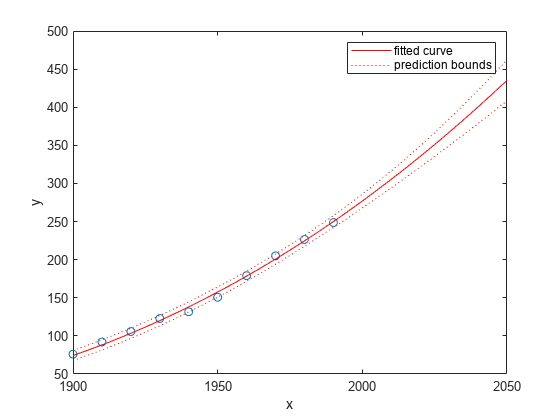
在外推法拟合范围内绘制拟合和预测区间图。默认情况下，拟合会在数据范围内绘制。要查看拟合后的外推值，请在绘制拟合之前将坐标轴的 x 上限设置为 2050。要绘制预测区间，请使用 predobs 或 predfun 作为绘图类型。

plot(cdate,pop,'o')
xlim([1900,2050])
hold on
plot(curvefit,'predobs')
hold off

3.5 获取模型方程

输入拟合名称可显示模型方程、拟合系数和拟合系数的置信区间。

curvefit

curvefit = 
     Linear model Poly3:
     curvefit(x) = p1*x^3 + p2*x^2 + p3*x + p4
       where x is normalized by mean 1890 and std 62.05
     Coefficients (with 95% confidence bounds):
       p1 =       0.921  (-0.9743, 2.816)
       p2 =       25.18  (23.57, 26.79)
       p3 =       73.86  (70.33, 77.39)
       p4 =       61.74  (59.69, 63.8)

如果只想获得模型方程，请使用公式。

formula(curvefit)

ans = 
'p1*x^3 + p2*x^2 + p3*x + p4'

3.6 获取系数名称和数值

通过名称指定系数。

p1 = curvefit.p1

p1 = 0.9210

p2 = curvefit.p2

p2 = 25.1834

获取所有系数名称。查看拟合方程（例如，f(x) = p1*x^3+… ) 来查看每个系数的模型项。

coeffnames(curvefit)

ans = 4x1 cell
    {'p1'}
    {'p2'}
    {'p3'}
    {'p4'}

获取所有系数值。

coeffvalues(curvefit)

ans = 1×4

    0.9210   25.1834   73.8598   61.7444

3.7 获取系数的置信区间

使用系数的置信界来帮助您评估和比较拟合。系数的置信区间决定了系数的准确性。界限相距甚远表示不确定性。如果线性系数的置信区间为零，这意味着您无法确定这些系数是否与零相差不大。如果某些模型项的系数为零，那么它们对拟合没有帮助。获取系数的置信区间
使用系数的置信界来帮助您评估和比较拟合。系数的置信区间决定了系数的准确性。界限相距甚远表示不确定性。如果线性系数的置信区间为零，这意味着您无法确定这些系数是否与零相差不大。如果某些模型项的系数为零，那么它们对拟合没有帮助。

confint(curvefit)

ans = 2×4

   -0.9743   23.5736   70.3308   59.6907
    2.8163   26.7931   77.3888   63.7981

3.8 检查拟合优度统计

要在命令行下获取拟合优度统计信息，您可以

• 打开曲线拟合器应用程序。在 "曲线拟合器 "选项卡的 "导出 "部分，单击 "导出 "并选择 “导出到工作区”，将拟合结果和拟合优度导出到工作区。

• 使用拟合函数指定 gof 输出参数。

重新创建拟合，指定 gof 和输出参数，以获取拟合优度统计信息和拟合算法信息。

[curvefit,gof,output] = fit(cdate,pop,'poly3','normalize','on')

curvefit = 
     Linear model Poly3:
     curvefit(x) = p1*x^3 + p2*x^2 + p3*x + p4
       where x is normalized by mean 1890 and std 62.05
     Coefficients (with 95% confidence bounds):
       p1 =       0.921  (-0.9743, 2.816)
       p2 =       25.18  (23.57, 26.79)
       p3 =       73.86  (70.33, 77.39)
       p4 =       61.74  (59.69, 63.8)
gof = struct with fields:
           sse: 149.7687
       rsquare: 0.9988
           dfe: 17
    adjrsquare: 0.9986
          rmse: 2.9682

output = struct with fields:
        numobs: 21
      numparam: 4
     residuals: [21x1 double]
      Jacobian: [21x4 double]
      exitflag: 1
     algorithm: 'QR factorization and solve'
    iterations: 1

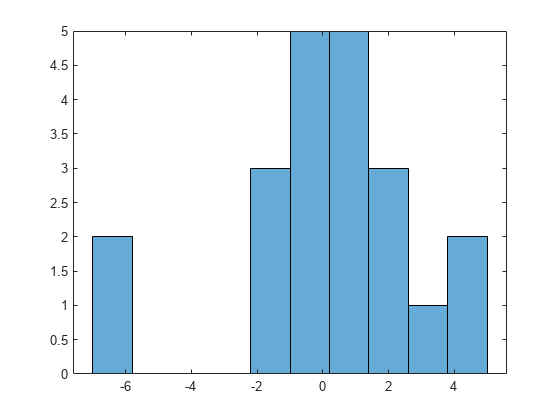
绘制残差直方图，寻找大致正态分布。

histogram(output.residuals,10)

3.9 绘制拟合图、数据图和残差图

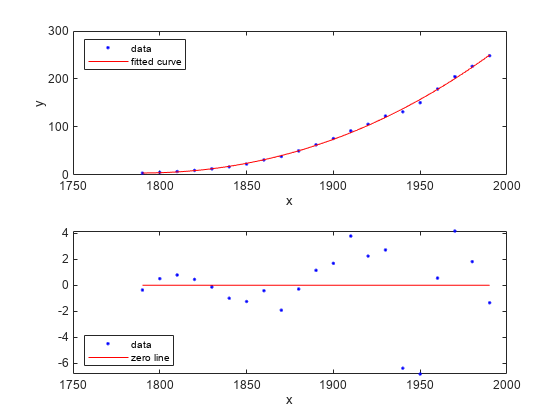
plot(curvefit,cdate,pop,'fit','residuals')
legend Location SouthWest
subplot(2,1,1)
legend Location NorthWest

3.10 查找方法

列出您可以使用的每种拟合的方法。

methods(curvefit)

cfit 类的方法：

argnames       category       cfit           coeffnames     coeffvalues    confint        dependnames    differentiate  feval          fitoptions     formula        indepnames     integrate      islinear       numargs        numcoeffs      plot           predint        probnames      probvalues     setoptions     type           

有关如何使用拟合方法的更多信息，请参阅 cfit。有关如何使用拟合方法的更多信息，请参阅 cfit。