发现新天地，欢迎访问小铬的主页(www.xiaocr.fun)

引言

本讲我们将介绍两种最为常用的相关系数：皮尔逊pearson相关系数和斯皮尔曼spearman等级相关系数。它们可用来衡量两个变量之间的相关性的大小，根据数据满足的不同条件，我们要选择不同的相关系数进行计算和分析（建模论文中最容易用错的方法）。

概念

• 总体——所要考察对象的全部个体叫做总体.
• 我们总是希望得到总体数据的一些特征（例如均值方差等）
• 样本——从总体中所抽取的一部分个体叫做总体的一个样本.

计算这些抽取的样本的统计量来估计总体的统计量：例如使用样本均值、样本标准差来估计总体的均值（平均 水平）和总体的标准差（偏离程度）。 例子： 我国10年进行一次的人口普查得到的数据就是总体数据。 大家自己在QQ群发问卷叫同学帮忙填写得到的数据就是样本数据。

皮尔逊相关系数

---

皮尔逊相关系数也可以看成是剔除了两个变量量纲影响，即将X和Y标准化后的协方差。

皮尔逊相关系数误区

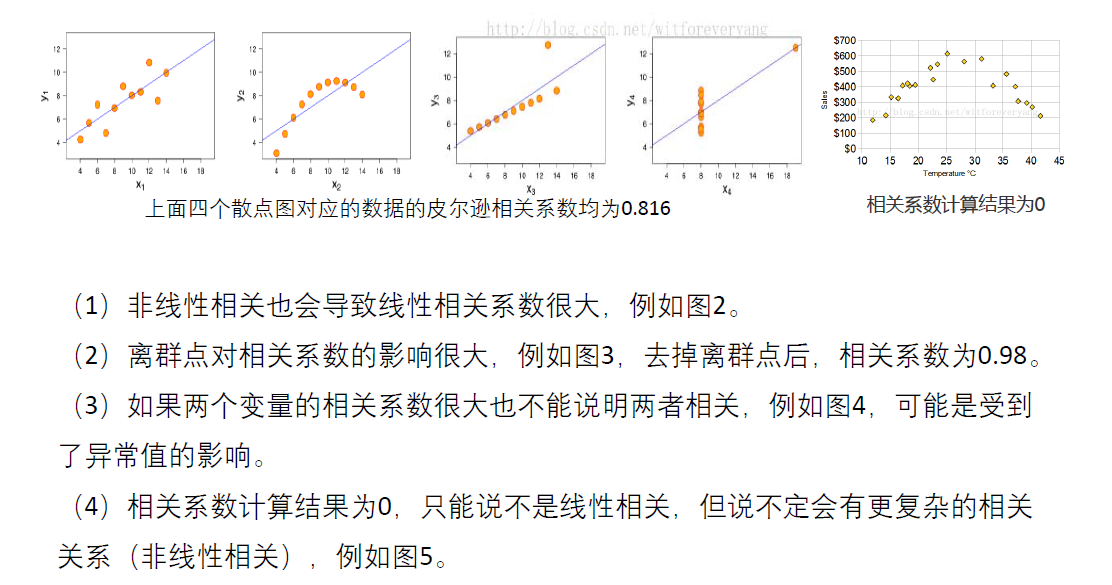
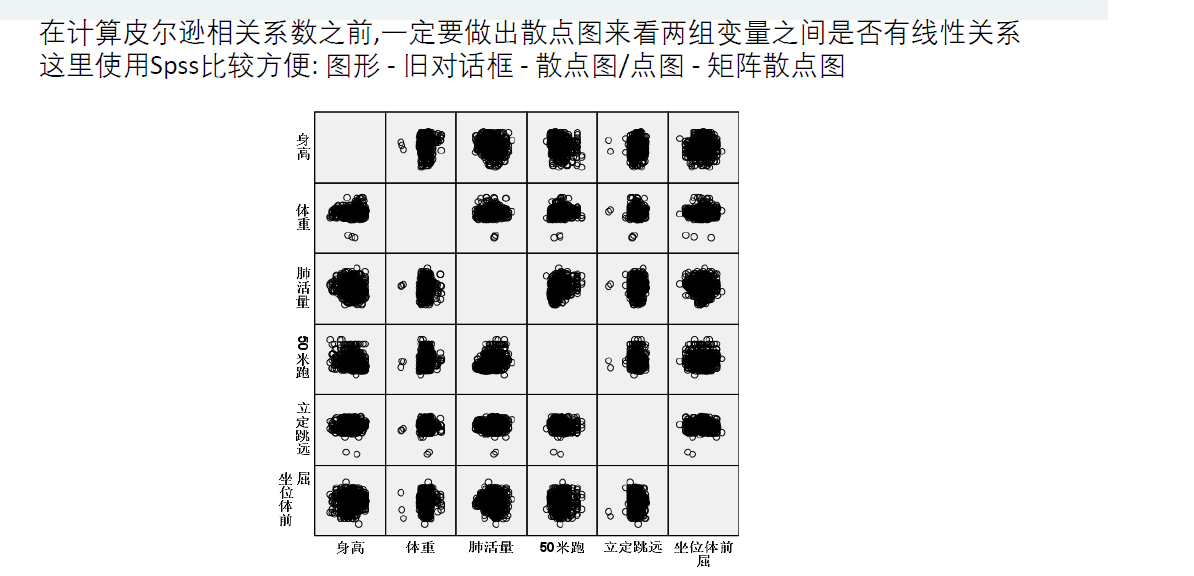
（1）如果两个变量本身就是线性的关系，那么皮尔逊相关系数绝对值大的就是相关性 强，小的就是相关性弱； （2）在不确定两个变量是什么关系的情况下，即使算出皮尔逊相关系数，发现很大，也不能说明那两个变量线性相关，甚至不能说他们相关，我们一定要画出散点图来看才行。

描述性统计

matlab代码

%% 手敲代码统计描述
MIN = min(Test); %每一列的最小值
MAX = max(Test); %每一列的最大值
MEAN = mean(Test);%每一列的均值
MEDIAN = median(Test);%每一列的中位数
SKEWNESS = skewness(Test);%每一列的偏度
KURTOSIS = kurtosis(Test);%每一列的峰度
STD = std(Test);%每一列的标准差
Result = [MIN;MAX;MEAN;MEDIAN;SKEWNESS;KURTOSIS;STD];%描述性矩阵

%% 计算各列的相关系数
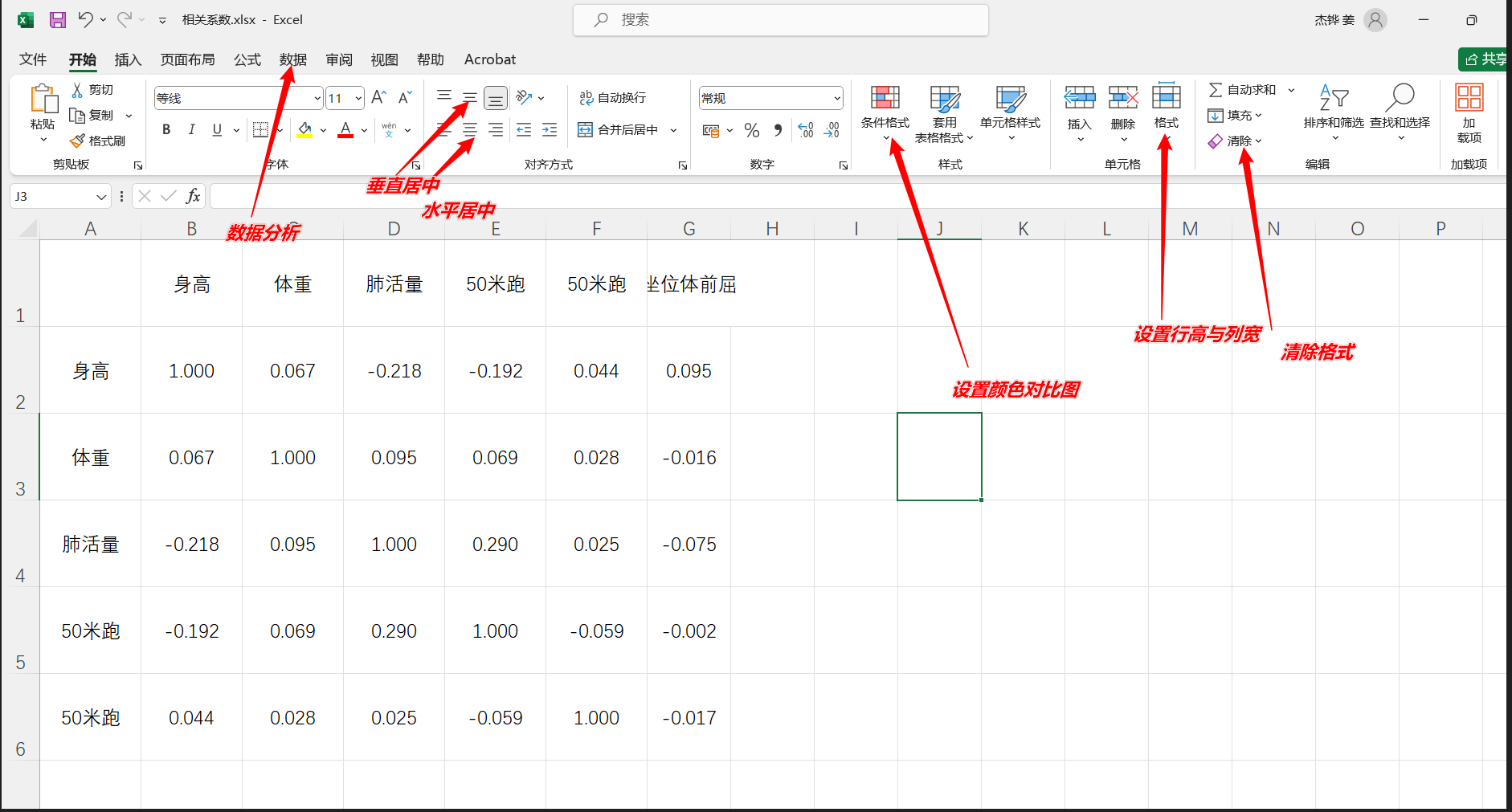
R = corrcoef(Test);   % correlation coefficient

excel操作

---

---

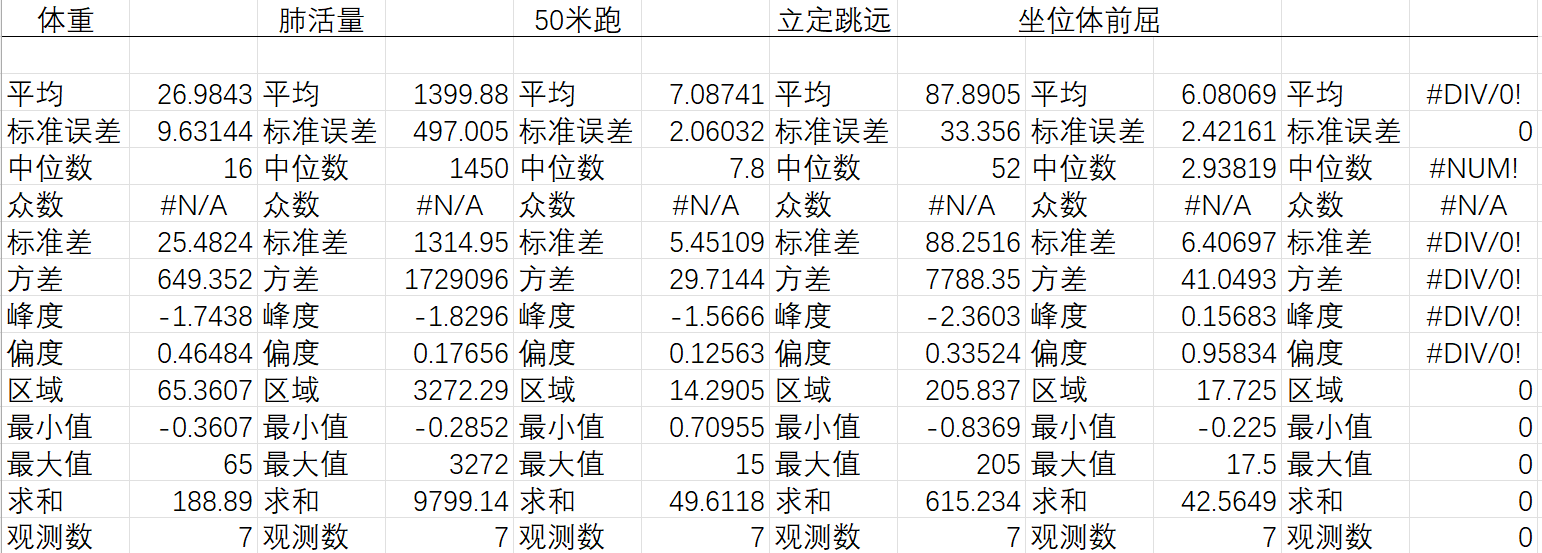
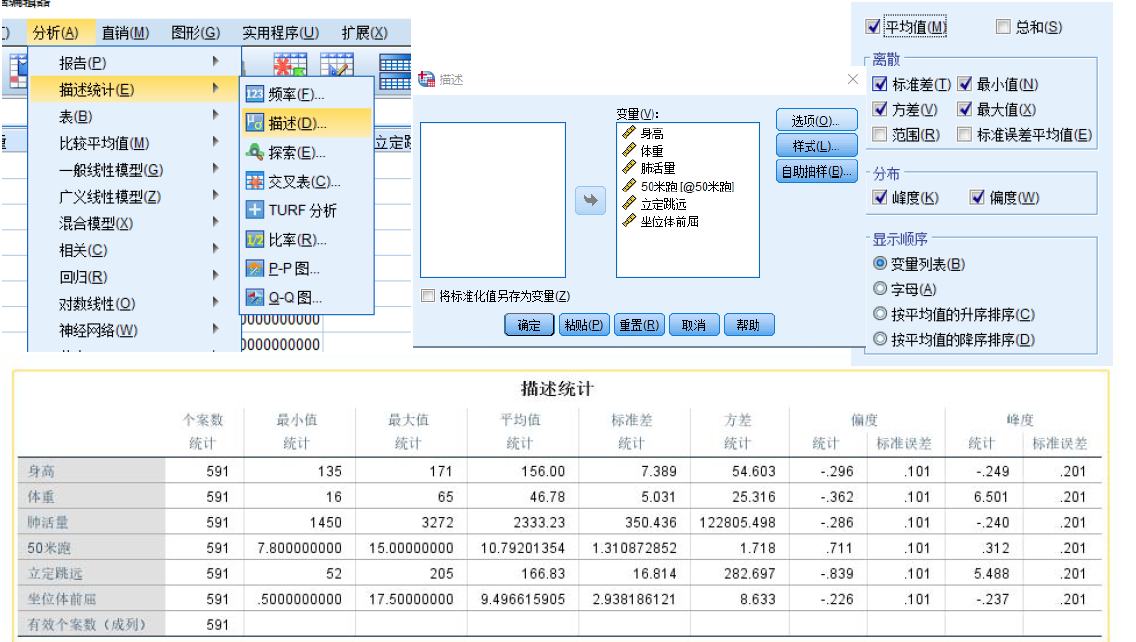
SPSS描述性

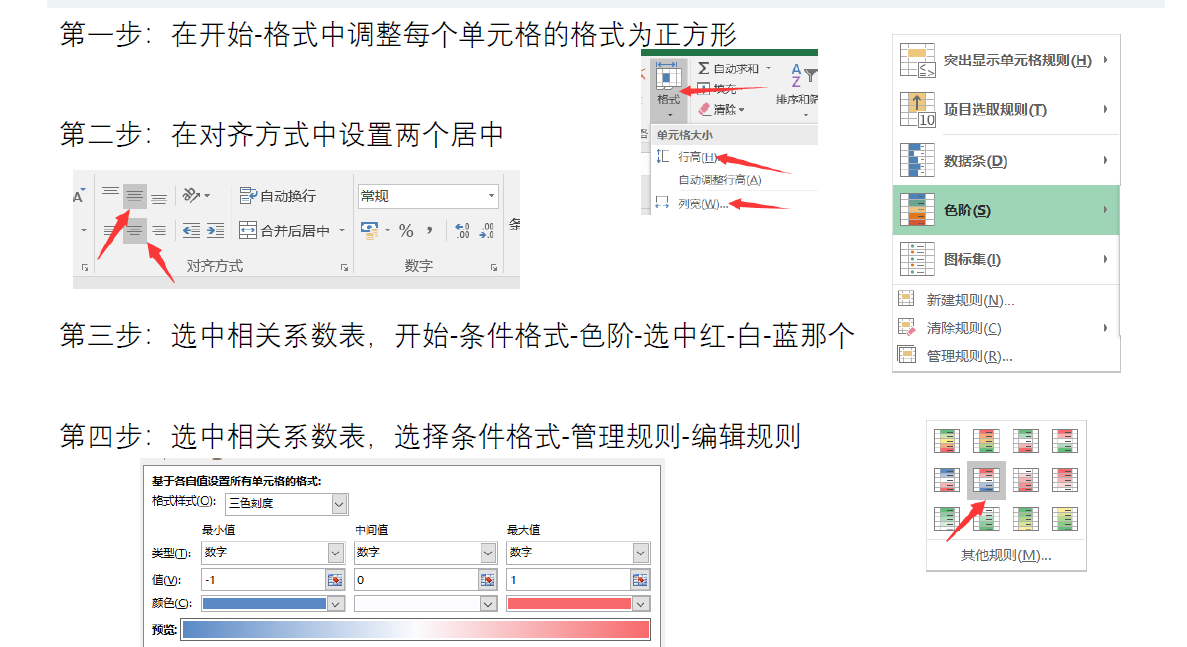
excel中美化系数表

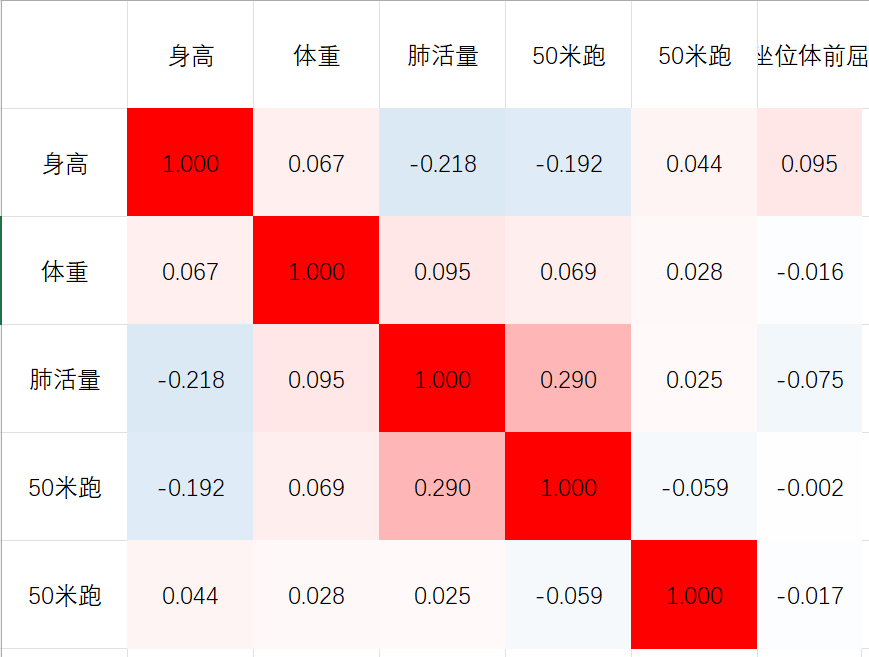
结果大概就是这样

---

对皮尔逊相关系数的假设性检验

• 第一步：提出原假设H0和备择假设H1（两个假设是截然相反的）

  假设我们计算出了一个皮尔逊相关系数r，我们想检验它是否显著的异于0那么我们可以这样设定原假设和备择假设：H0 ：r = 0. H1 r != 0

• 第二步

• 

*

---

• 

---

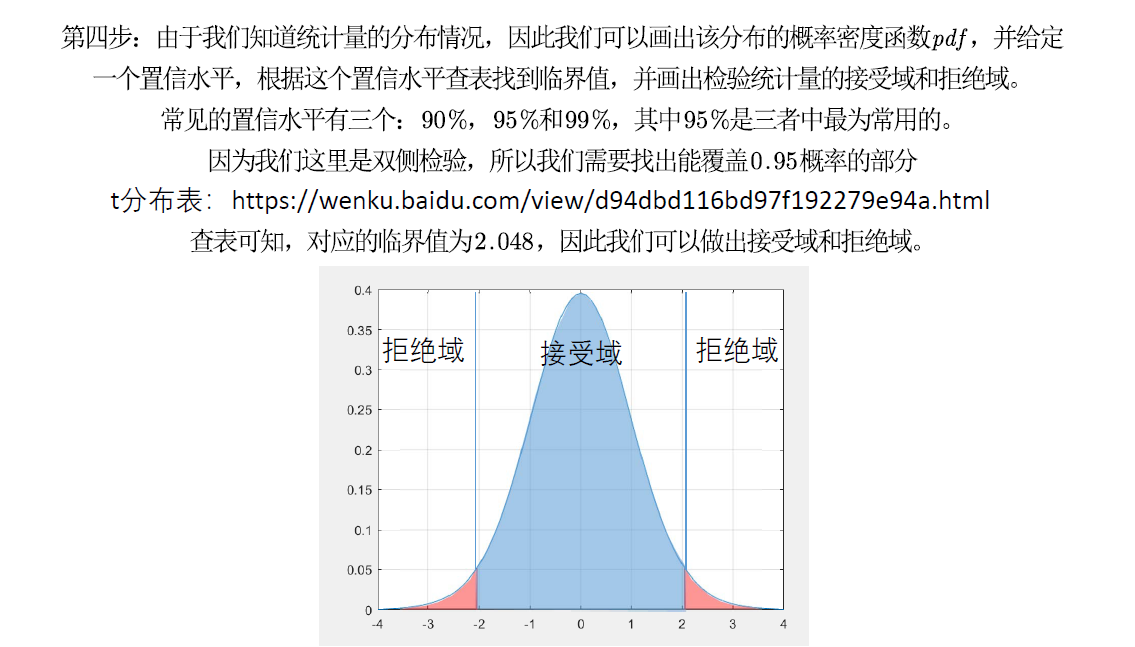
P值判断法

如图:

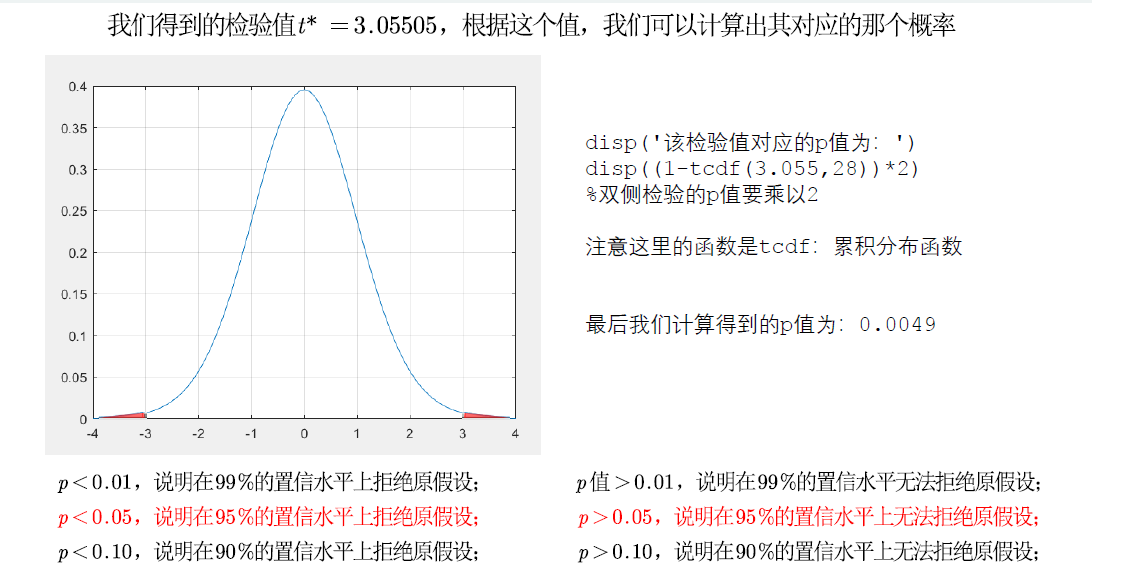
代码实现

• 计算相关系数R与R的P值

[R,P] = corrcoef(Test)

• 标记不同显著性

P < 0.01 %返回逻辑矩阵，标记三颗星的位置
(P < 0.05) .* (P > 0.01)%标记两颗星的位置
(P < 0.1) .8 (P > 0.05)%标记一颗星的位置

利用SPSS计算

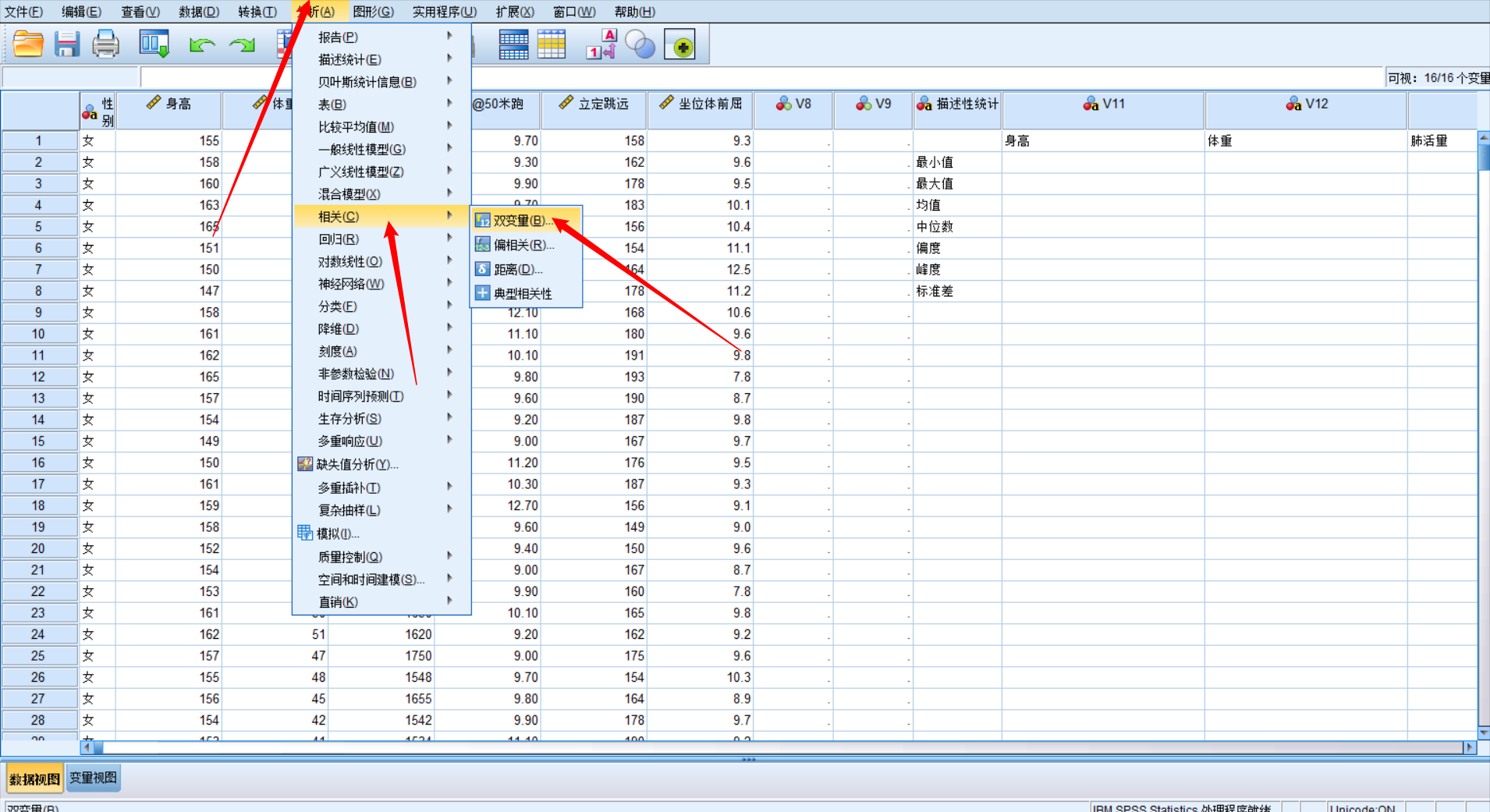
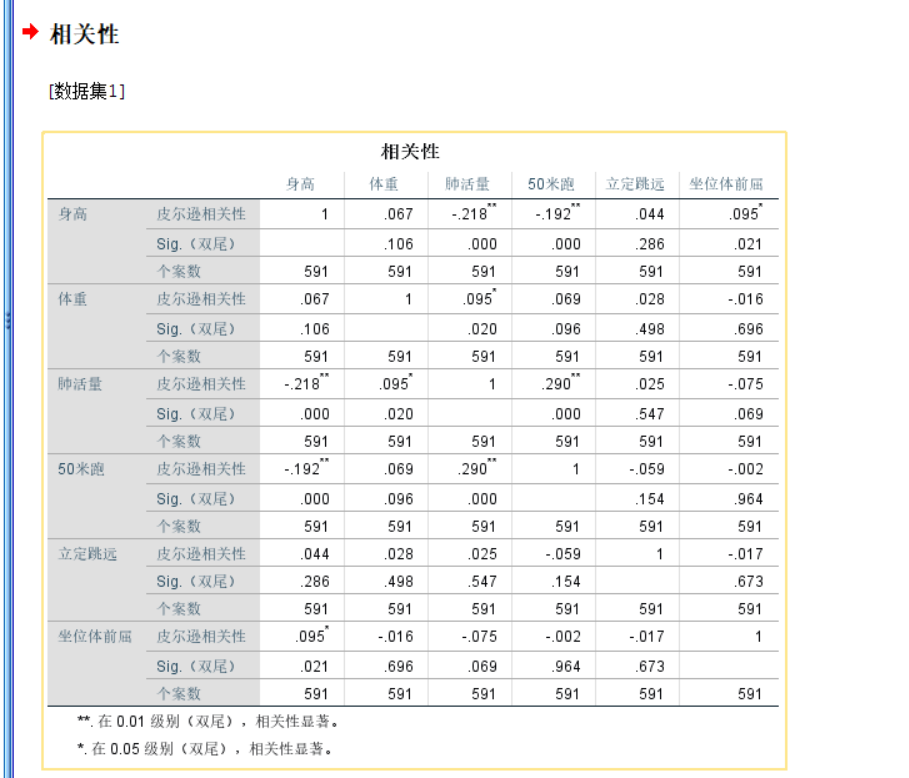
皮尔逊相关系数假设检验的条件

• 第一， 实验数据通常假设是成对的来自于正态分布的总体。因为我们在求皮尔逊相关性系数以后，通常还会用t检验之类的方法来进行皮尔逊相关性系数检验，而t检验是基于数据呈正态分布的假设的。
• 第二， 实验数据之间的差距不能太大。皮尔逊相关性系数受异常值的影响比较大。
• 第三：每组样本之间是独立抽样的。构造t统计量时需要用到。

正态性检验

由于皮尔逊相关系数假设检验的很重要的条件是数据符合正态分布，所以我们很有必要进行正态性检验。

正态分布JB检验

雅克‐贝拉检验(Jarque‐Bera test)

---

假设检验的步骤:

H0:该随机变量服从正态分布.H1:该随机变量不服从正态分布.然后计算该变量的偏度和峰度，得到检验值JB*，并计算出其对应的p值,将p值与0.05比较，如果小于0.05则可拒绝原假设，否则我们不能拒绝原假设

峰度与偏度

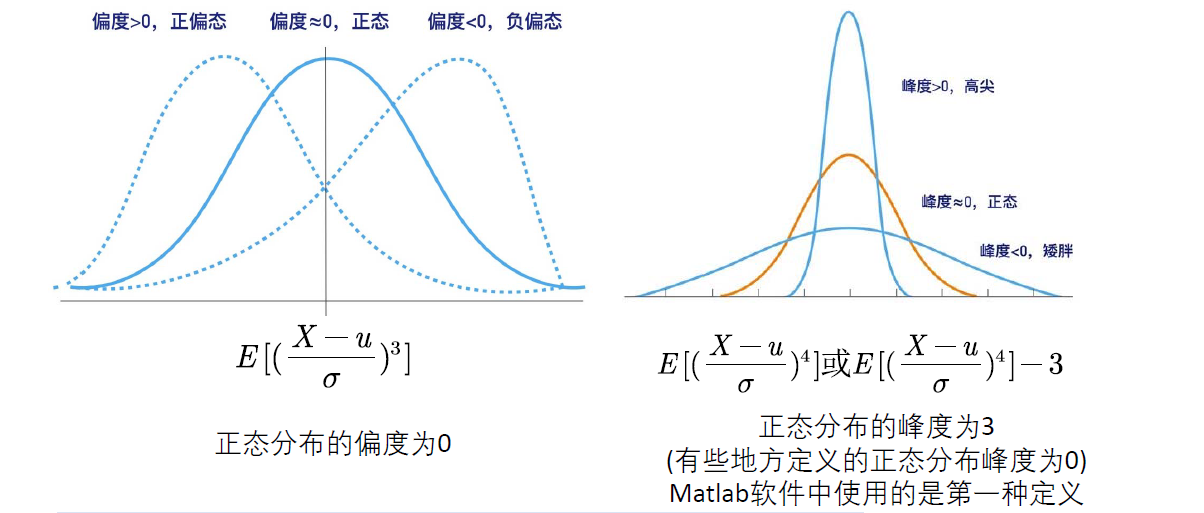
代码:

x = normrnd(2,3,100,1);
% 生成100*1的随机向量，每个元素是均值为2，标准差为3的正态分布
skewness(x) %偏度
kurtosis(x) %峰度

matlab代码实现

MATLAB中进行JB检验的语法：[h,p] = jbtest(x,alpha) 当输出h等于1时，表示拒绝原假设；h等于0则代表不能拒绝原假设。 alpha就是显著性水平，一般取0.05，此时置信水平为1‐0.05=0.95

x就是我们要检验的随机变量，注意这里的x只能是向量。

%% 正态分布检验
% 检验第一列数据是否为正态分布
[h,p] = jbtest(Test(:,1),0.05)
% 用循环检验所有列的数据
n_c = size(Test,2); % number of column 数据的列数
H = zeros(1,6);
P = zeros(1,6);
for i = 1:n_c
[h,p] = jbtest(Test(:,i),0.05);
H(i)=h;
P(i)=p;
end
disp(H)
disp(P)

小样本3≤n≤50：Shapiro-wilk检验

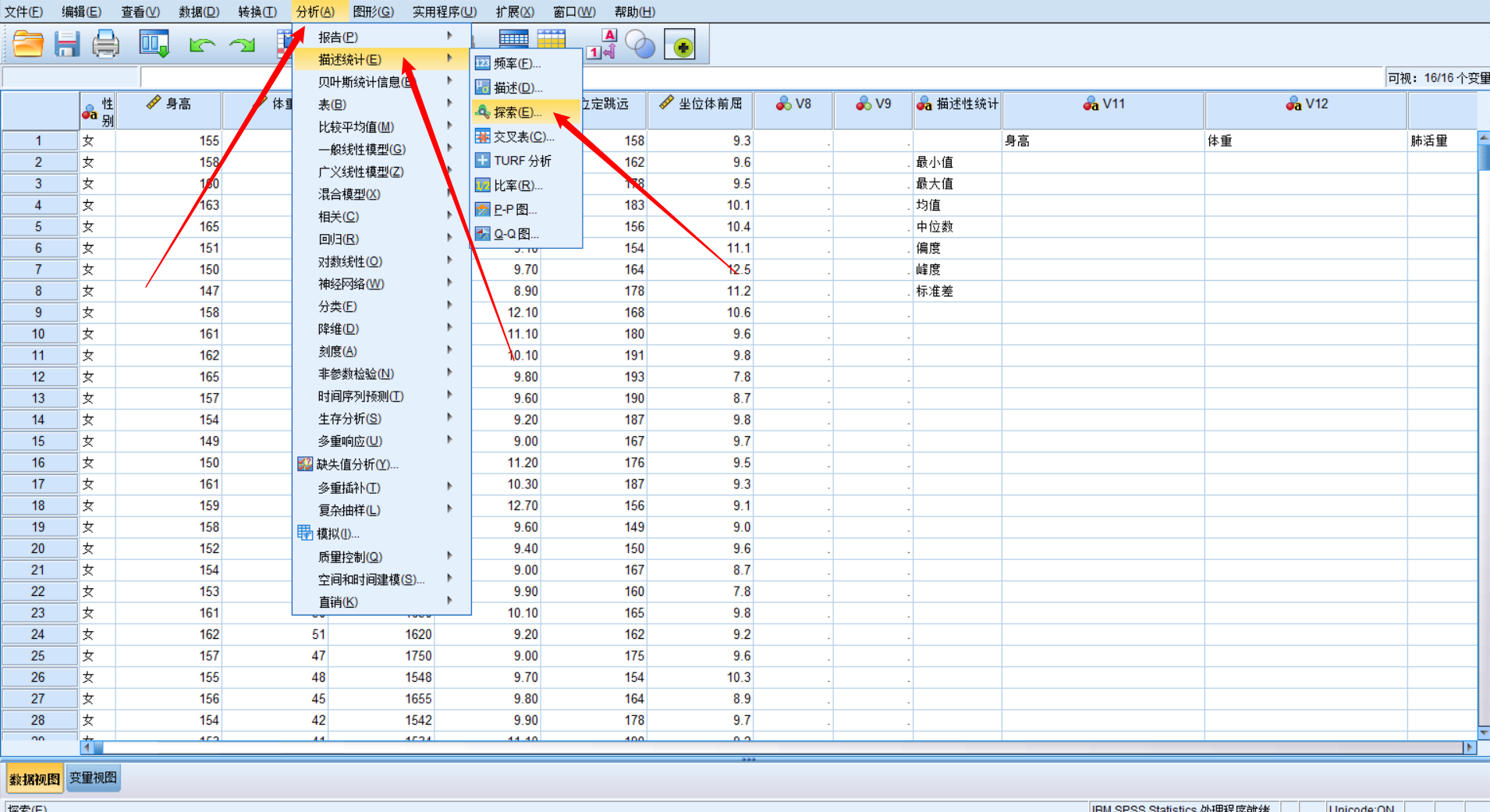
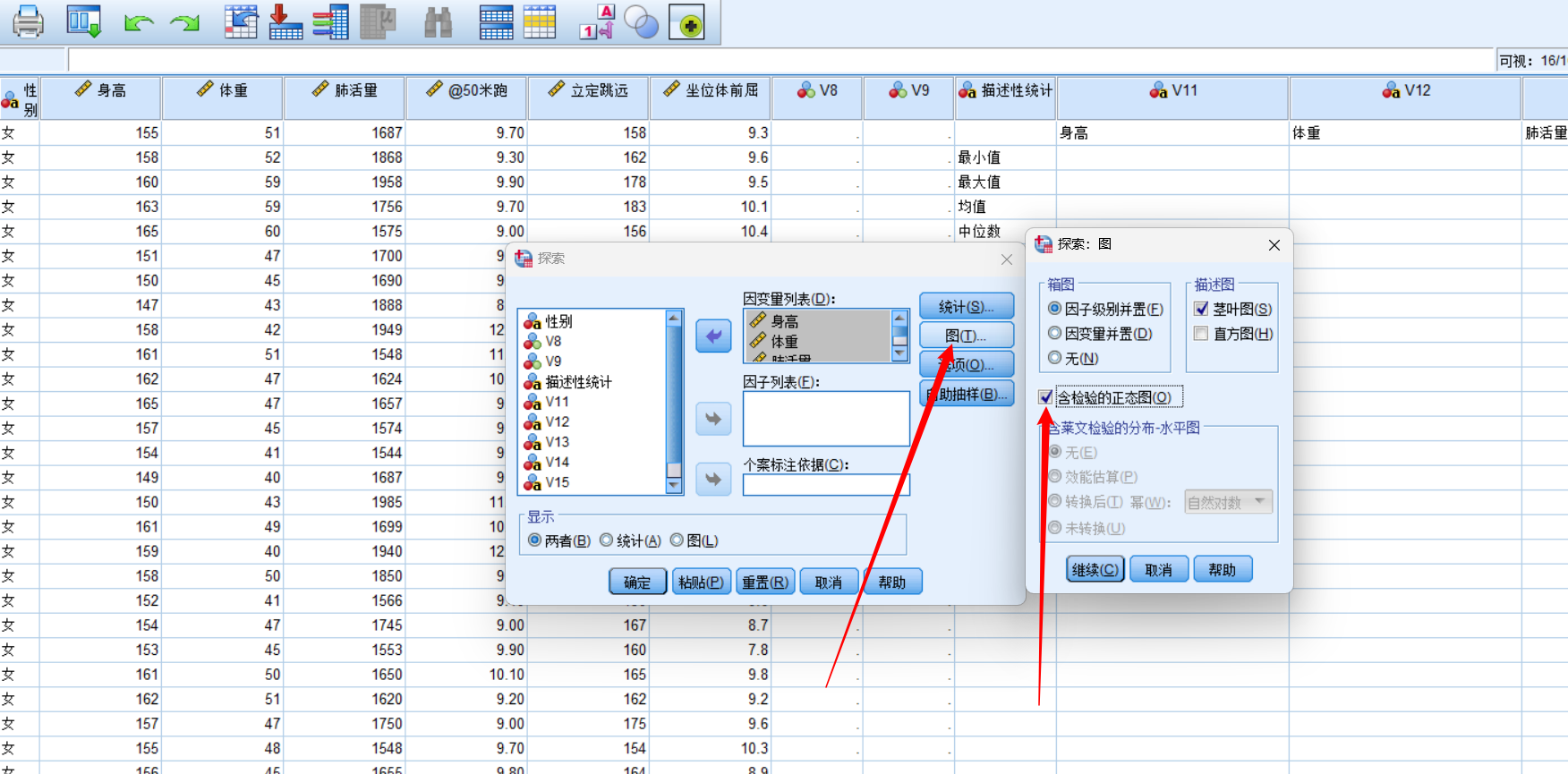
得到结果:

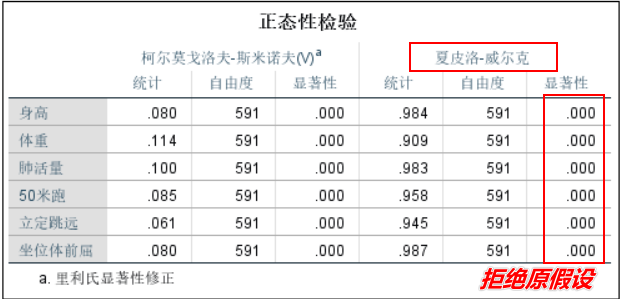
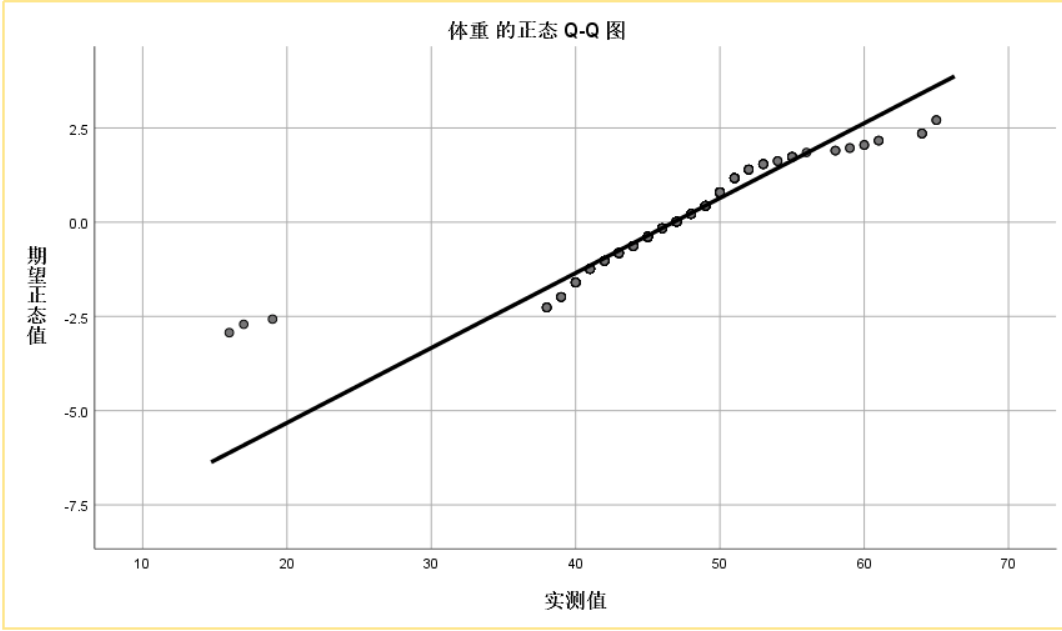
QQ图

在统计学中，Q‐Q图（Q代表分位数Quantile）是一种通过比较两个概率分布的分位数对这两个概率分布进行比较的概率图方法。 首先选定分位数的对应概率区间集合，在此概率区间上，点(x,y)对应于第一个分布的一个分位数x和第二个分布在和x相同概率区间上相同的分位数。 这里，我们选择正态分布和要检验的随机变量，并对其做出QQ图，可想而知，如果要检验的随机变量是正态分布，那么QQ图就是一条直线。要利用Q‐Q图鉴别样本数据是否近似于正态分布,只需看Q‐Q图上的点 是否近似地在一条直线附近。（要求数据量非常大）

斯皮尔曼相关系数

定义:

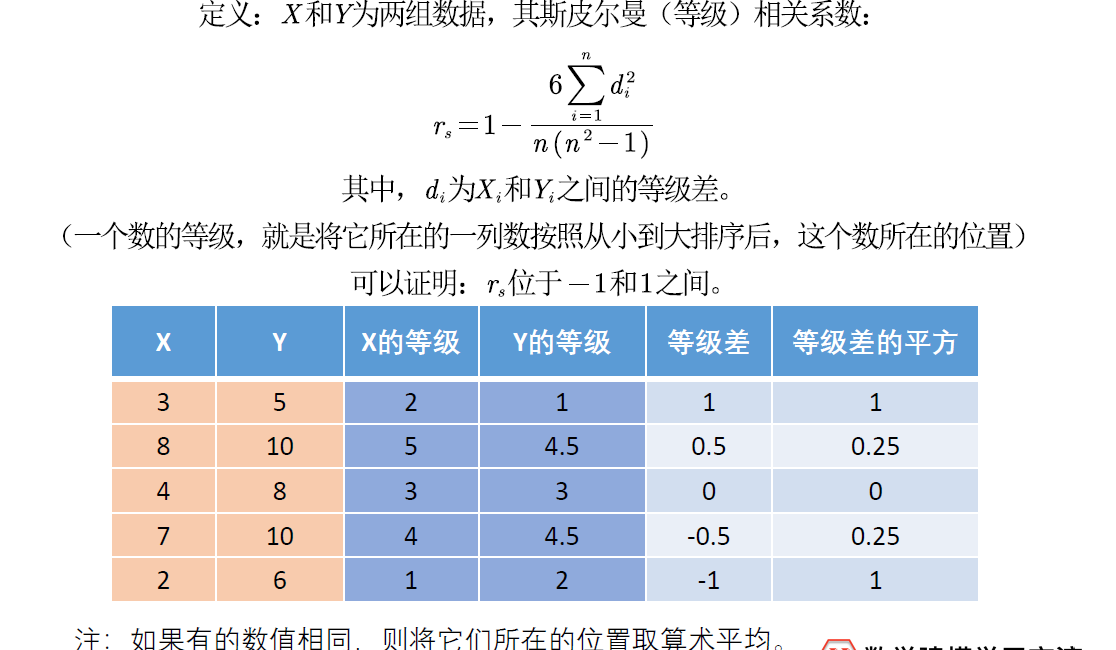
另一种定义:

---

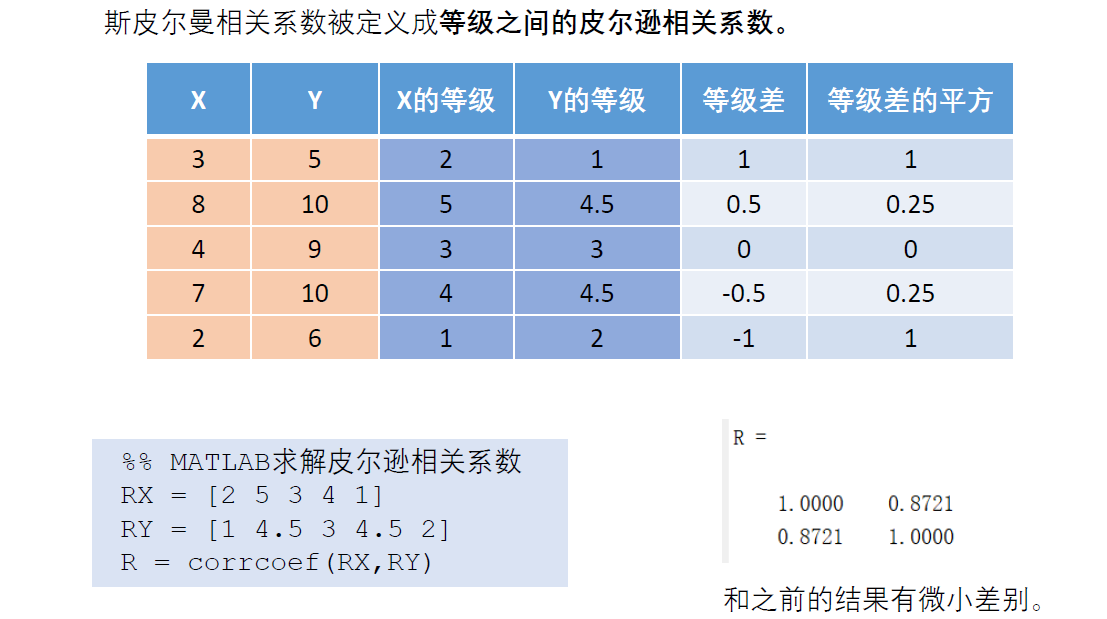
matlab的内置函数用的是第二种定义

matlab计算

X = [3 8 4 7 2]' % 一定要是列向量，一撇'表示求转置
Y = [5 10 9 10 6]'
coeff = corr(X , Y , 'type' , 'Spearman')

利用spss计算

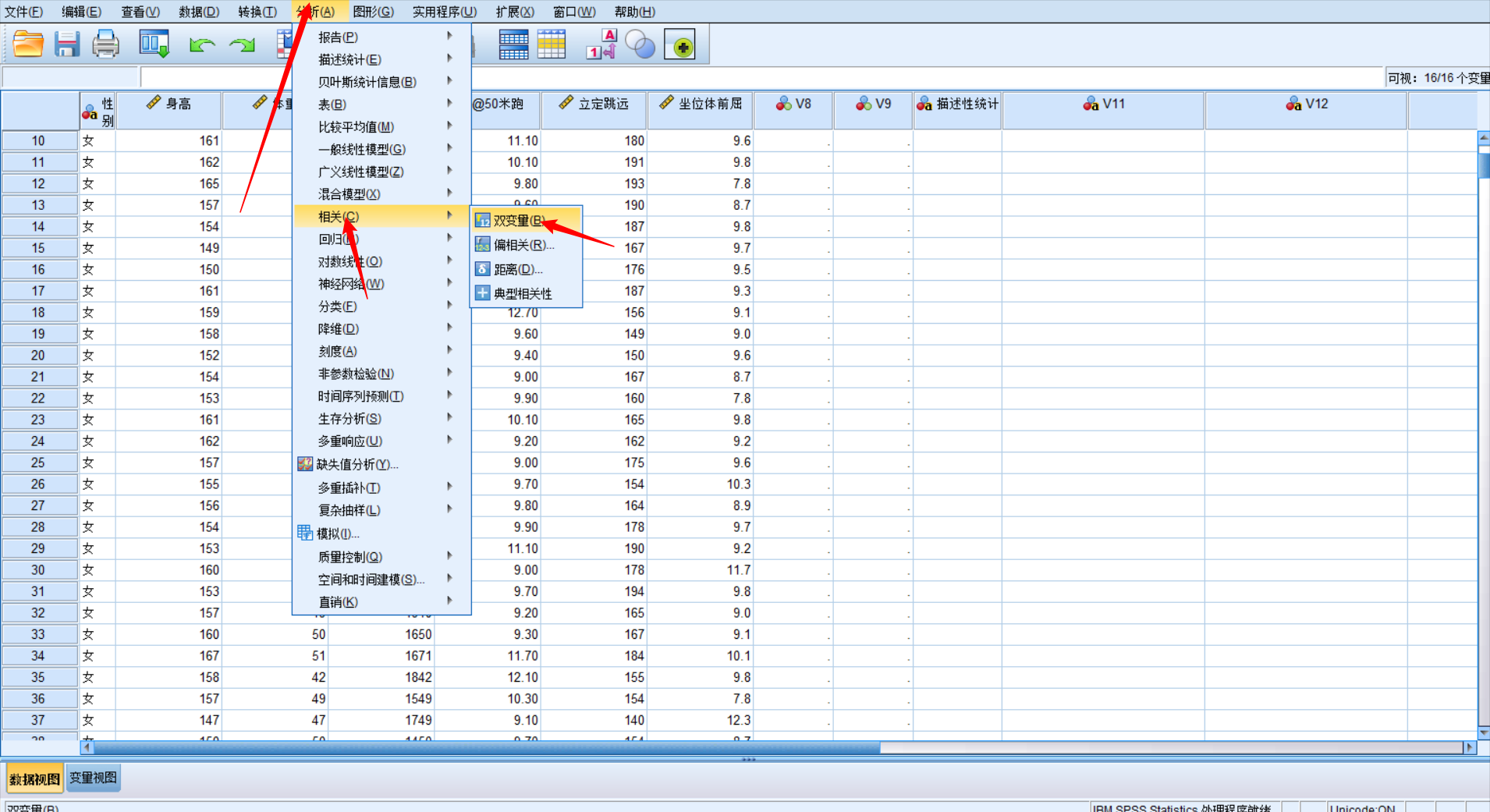
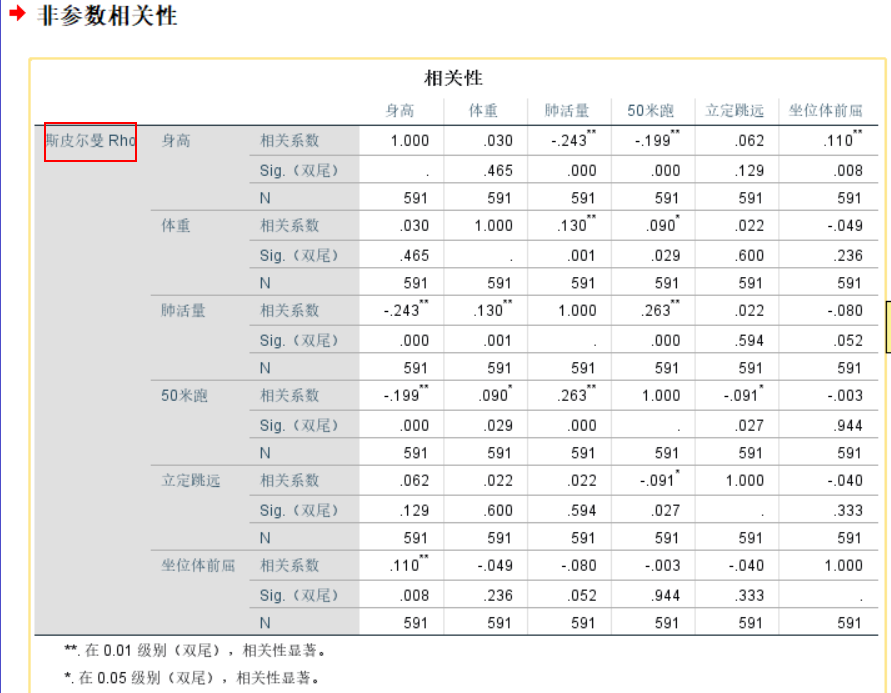
斯皮尔曼相关系数假设性检验

小样本(n小于30)

直接用查表法

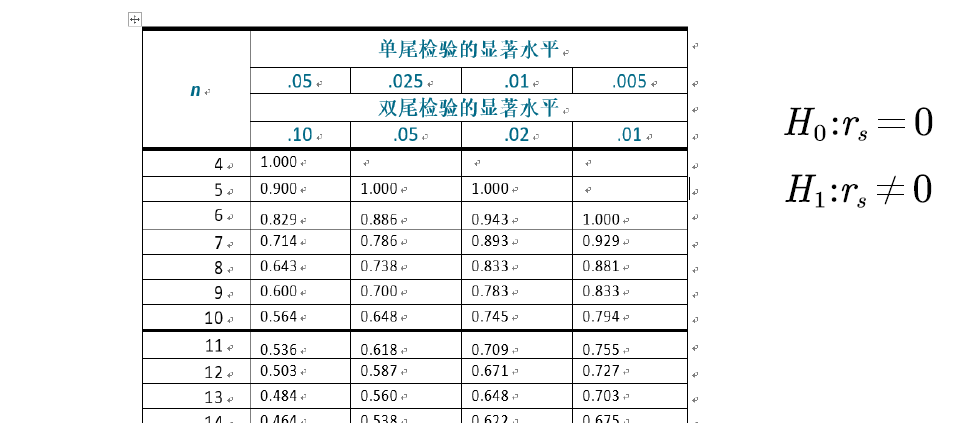
大样本

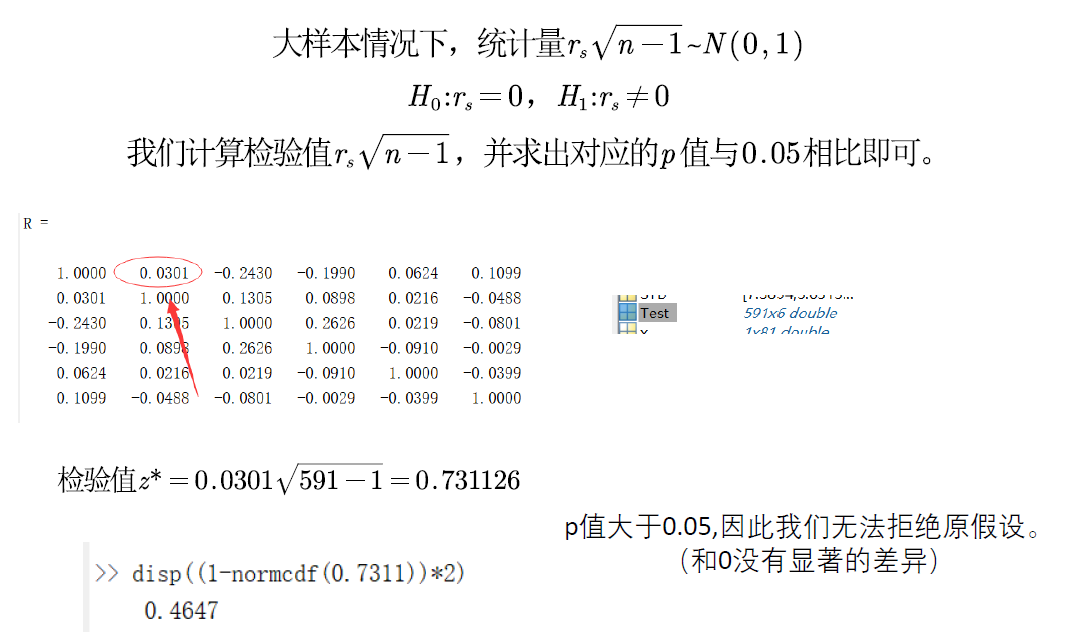
两大相关系数比较

斯皮尔曼相关系数和皮尔逊相关系数选择:

• 1.连续数据，正态分布，线性关系，用pearson相关系数是最恰当，当然用spearman相关系数也可以， 就是效率没有pearson相关系数高。
• 2.上述任一条件不满足，就用spearman相关系数，不能用pearson相关系数。
• 3.两个定序数据之间也用spearman相关系数，不能用pearson相关系数。
• 定序数据是指仅仅反映观测对象等级、顺序关系的数据，是由定序尺度计量形成的，表现为类别，可以进行排序，属于品质数据。 例如：优、良、差； 我们可以用1表示差、2表示良、3表示优，但请注意，用2除以1得出的2并不代表任何含义。定序数据最重要的意义代表了一组数据中的某种逻辑顺序。

  本文由博客一文多发平台 OpenWrite 发布！