本文仅供学习,不作任何商业用途,严禁转载。绝大部分资料来自----数字集成电路——电路、系统与设计(第二版)及中国科学院段成华教授PPT
超大规模集成电路设计----CMOS反相器(五)
- 5.1 静态CMOS反相器综述
- 5.1.1 静态CMOS反相器优点
- 5.1.2 静态CMOS反相器的VTC曲线
- 5.1.3 静态CMOS反相器瞬态响应简要分析
- 5.2 CMOS反相器稳定性评估——静态特性
- 5.2.1 开关阈值 V M V_M VM
- PMOS与NMOS比例对开关阈值影响详细分析
- 5.2.2 噪声容限
- 5.3.3 再谈稳定性
- 器件参数的变化
- 降低电源电压
- 5.3 CMOS反相器的动态特性
- 5.3.1 计算电容值
- 5.3.2 传播延时:一阶分析
- 5.3.3 从设计角度考虑传播延时
- 5.3.3.1 PMOS与NMOS---β参数
- 5.3.3.2 超大负载时单个反相器尺寸确定
- 5.3.3.2 超大负载时反相器链尺寸、级数确定
- 反相器链例题
- 5.3.3.3 输入信号上升下降时间对传播延时的影响
- 5.3.3.4 存在互连线时的延时
- 5.4 功耗、能量和能量延时
- 5.4.1 动态功耗
- 5.4.1.1 充放电电容引起的功耗
- 5.4.1.2 直流通路引起的功耗
- 5.4.2 静态功耗
- 漏源与衬底之间的漏电
- 亚阈值电流
- 5.4.3 总功耗
为什么要学习这一章:CMOS反相器充斥着组合电路和时序电路的各个角落。在本篇博文中,我们将首先对CMOS反相器的静态和动态特性进行分析,然后再分析各种负载强度下,我们应该如何合理地设计反相器。最后我们对CMOS反相器的功耗进行分析。标黄部分属于必须掌握的部分,黑体部分表示强调部分,有助于理解,对于普通字体部分,时间紧急的浏览者可以选择忽略,对于初学者,建议博文每部分都需要连贯阅读。
5.1 静态CMOS反相器综述
5.1.1 静态CMOS反相器优点
为什么我们要用CMOS反相器,它究竟有什么魔力
- 输出摆幅为电源轨。
- 输出逻辑电平与器件相对尺寸无关,晶体管可做到当前工艺下的最小,为无比逻辑。
- 静态时,输出点与VDD或GND有一个有限电阻的通路,具有低输出阻抗,所以对噪声不敏感。
- 输入电阻极高,理论上可以有无穷大的扇出。
- 稳态情况下电源线和地线无直接通路,没有电流(忽略漏电流),意味着没有静态功率。

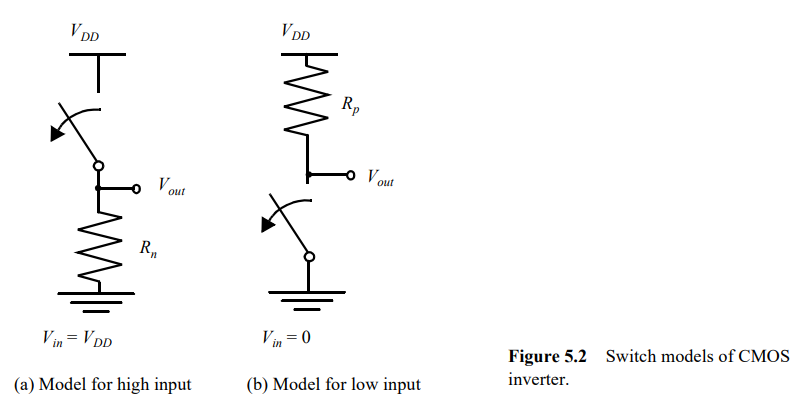
5.1.2 静态CMOS反相器的VTC曲线
具体推导看书即可,这里直接给出VTC曲线。
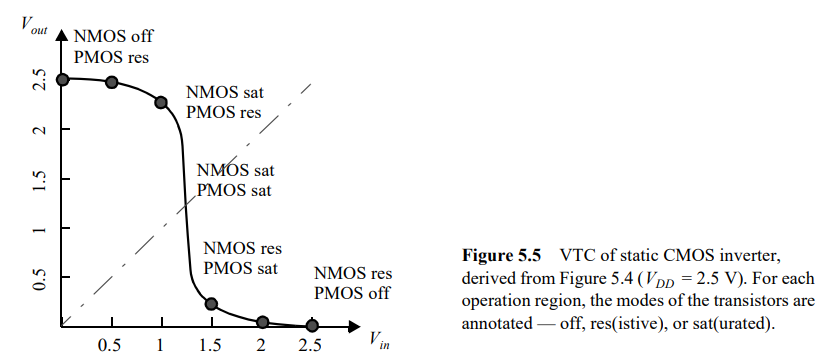
要记住不同的输入电压,对应NMOS管和PMOS管的工作状态
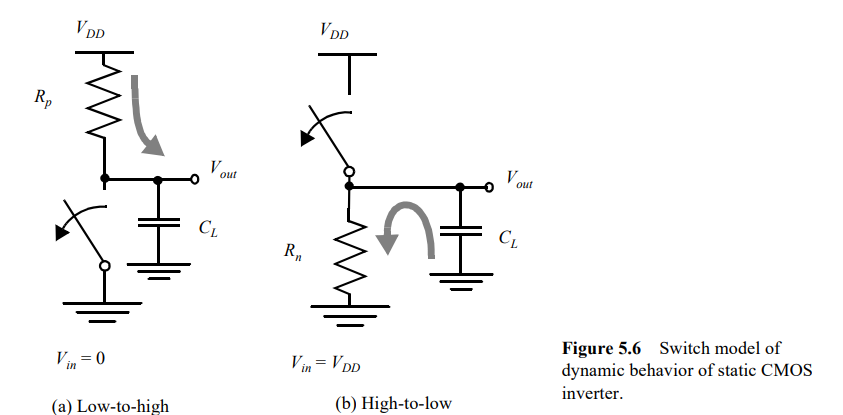
5.1.3 静态CMOS反相器瞬态响应简要分析
t
P
H
L
=
f
(
R
o
n
,
C
L
)
=
0.69
R
o
n
C
L
t_{PHL}=f(R_{on},C_L)=0.69R_{on}C_L
tPHL=f(Ron,CL)=0.69RonCL,从这个式子我们可以看出,反相器的速度取决于MOS管的等效电阻和负载电容,那么究竟该如何降低这个传播延时呢,后续我们将进行讨论。
5.2 CMOS反相器稳定性评估——静态特性
V O H = V D D V O L = G N D V_{OH}=VDD V_{OL}=GND VOH=VDDVOL=GND,在这一前提下,我们来推导 V M , V I H , V I L V_M,V_{IH},V_{IL} VM,VIH,VIL及噪声容限的精确值。即我们分析反相器的稳定性是通过分析反相器的噪声容限来实现的。
5.2.1 开关阈值 V M V_M VM
V
M
V_M
VM 定义在
V
i
n
=
V
o
u
t
V_{in}=V_{out}
Vin=Vout的点,反映在VTC曲线上就是y=x这条直线与VTC曲线的交点横坐标。
因为当输入电压在开关阈值附近时,PMOS和NMOS均处于饱和状态,所以可以得到下面这个式子
k
n
V
D
S
A
T
n
(
V
M
−
V
T
n
−
V
D
S
A
T
n
2
)
+
k
p
V
D
S
A
T
p
(
V
M
−
V
D
D
−
V
T
p
−
V
D
S
A
T
p
2
)
=
0
k_nV_{DSATn}\bigg(V_M-V_{Tn}-\frac{V_{DSATn}}{2}\bigg)+k_pV_{DSATp}\bigg(V_M-V_{DD}-V_{Tp}-\frac{V_{DSATp}}{2}\bigg)=0
knVDSATn(VM−VTn−2VDSATn)+kpVDSATp(VM−VDD−VTp−2VDSATp)=0
化简得
V
M
=
(
V
T
n
+
V
D
S
A
T
n
2
)
+
r
(
V
D
D
+
V
T
p
+
V
D
S
A
T
p
2
)
1
+
r
V_M=\frac{\left(V_{Tn}+\frac{V_{DSATn}}{2}\right)+r\Big(V_{DD}+V_{Tp}+\frac{V_{DSATp}}{2}\Big)}{1+r}
VM=1+r(VTn+2VDSATn)+r(VDD+VTp+2VDSATp)
其中
r
=
k
p
V
D
S
A
T
p
k
n
V
D
S
A
T
n
=
υ
s
a
t
p
W
p
υ
s
a
t
n
W
n
r=\frac{k_pV_{DSATp}}{k_nV_{DSATn}}=\frac{\mathbf{\upsilon}_{satp}W_p}{\mathbf{\upsilon}_{satn}W_n}
r=knVDSATnkpVDSATp=υsatnWnυsatpWp
为了分析方便,我们将上面的式子简化,得到
V
M
≈
r
V
D
D
1
+
r
V_M\approx\frac{rV_{DD}}{1+r}
VM≈1+rrVDD
以后分析开关阈值,我们都只看这个简化的式子。
简单观察这个式子,我们发现如果r越大,则开关阈值就越大,直观的物理理解就是,r越大表明PMOS管子做的比NMOS越大,那么PMOS上拉能力就强,这样我要把输出电压下拉就需要更大的输入电压,这样开关阈值就增大了。
假如工程要求给定开关阈值,要求我们求PMOS和NMOS的大小比,那就根据下式来决定。
(
W
/
L
)
p
(
W
/
L
)
n
=
k
n
′
V
D
S
A
T
n
(
V
M
−
V
T
n
−
V
D
S
A
T
n
/
2
)
k
p
′
V
D
S
A
T
p
(
V
D
D
−
V
M
+
V
T
p
+
V
D
S
A
T
p
/
2
)
\frac{(W/L)_p}{(W/L)_n}=\frac{k'_nV_{DSATn}(V_M-V_{Tn}-V_{DSATn}/2)}{k'_pV_{DSATp}(V_{DD}-V_M+V_{Tp}+V_{DSATp}/2)}
(W/L)n(W/L)p=kp′VDSATp(VDD−VM+VTp+VDSATp/2)kn′VDSATn(VM−VTn−VDSATn/2)
一个经典示例,0.25um下,给CMOS反相器2.5V供电,若要求开关阈值为1.25V,即电源电压的一半,则此时
(
W
/
L
)
p
(
W
/
L
)
n
=
3.5
\frac{(W/L)_p}{(W/L)_n}=3.5
(W/L)n(W/L)p=3.5,最好是记住这个比例值
PMOS与NMOS比例对开关阈值影响详细分析
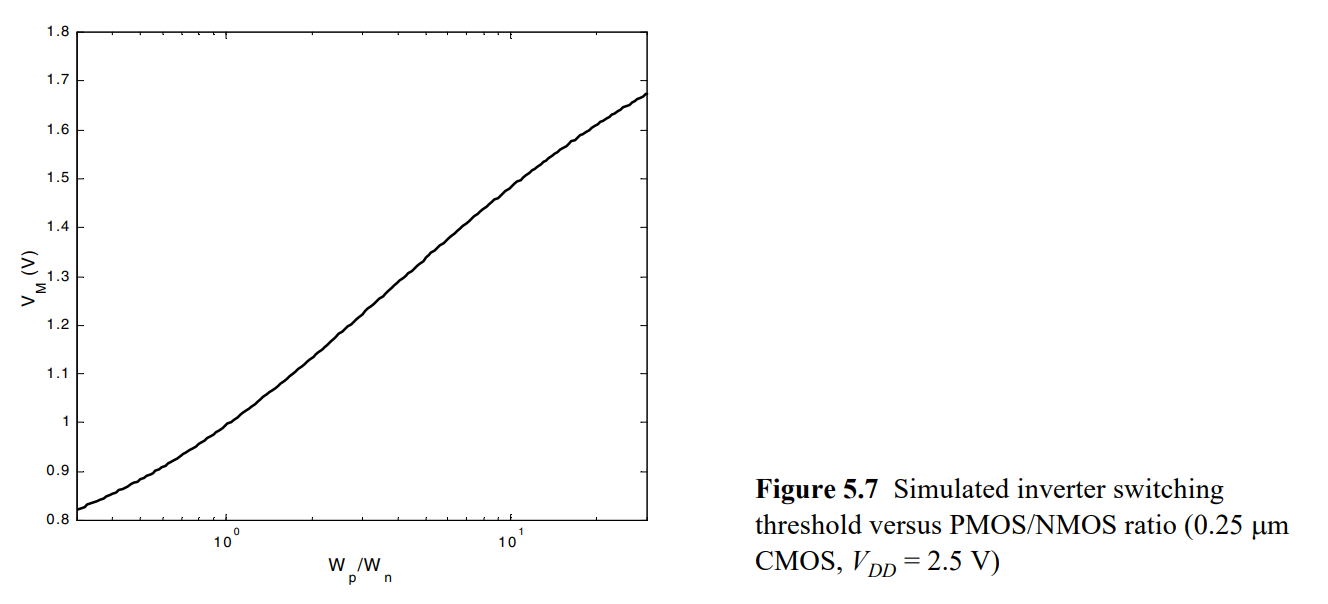
观察这个图可以得到如下信息
- VM对于器件比值的变化相对没想象的那么敏感,较小的比值变化对VM影响不大,这降低了对工艺准度的依赖。
- 可以利用PMOS和NMOS宽度比值变化来改变开关阈值从而主动制作一个VTC曲线不对称的CMOS反相器。具体应用如下图。
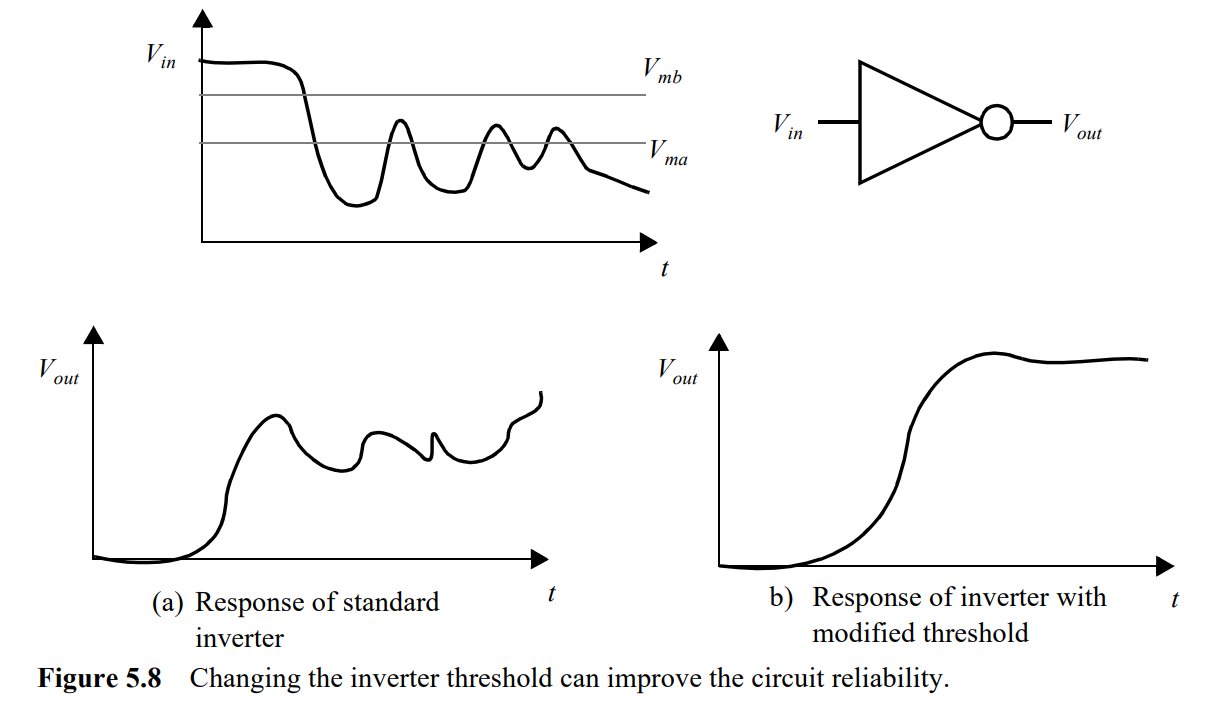
观察上图,对于Vma的阈值,输出响应如a所示,跳变非常多,但是如果把阈值改成Vmb,输出就会变得光滑。
5.2.2 噪声容限
对于一般情况,定义 V I H V_{IH} VIH和 V I L V_{IL} VIL为VTC曲线上 d V o u t d V i n = − 1 \begin{aligned}\frac{\mathrm{d}V_{out}}{\mathrm{d}V_{in}}&=-1\end{aligned} dVindVout=−1的两个点,这个时候反相器的小信号增益g=-1,这样可以推导出 V I H V_{IH} VIH和 V I L V_{IL} VIL的解析表达式,但是过于复杂了,下面我们采用一种更合理的手工分析方法来分析。
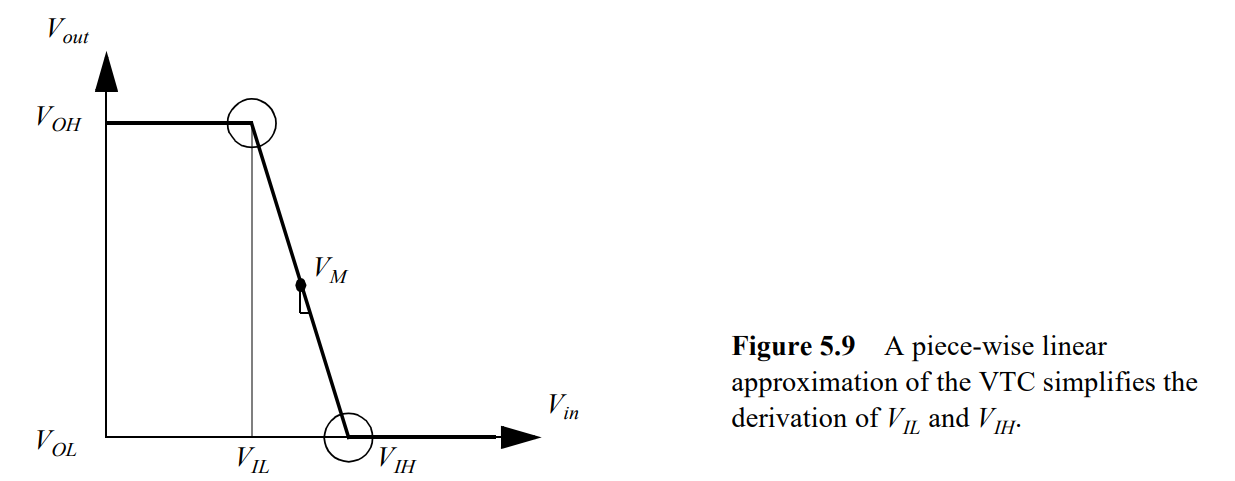
我们先利用VTC曲线找到VM,然后求出VM处的斜率曲线,让这个斜率曲线与Vout=VOH和Vout=VOL相交,得到的两个点分别就是VIL和VIH。
那么该如何推导出VIH和VIL用VM和g表达的式子呢?请看下面的推导。
- 首先我们先把过VM且斜率为g的曲线表达出来 V o u t − V M = g ( V i n − V M ) V_{out}-V_M=g(V_{in}-V_M) Vout−VM=g(Vin−VM)
- 令Vout=0得到 V I H = V M − V M g V_{IH}=V_M-\frac{V_M}g VIH=VM−gVM
- 令Vout=VDD得到 V I L = V M + V D D − V M g V_{IL}~=~V_M+\frac{V_{DD}-V_M}g VIL = VM+gVDD−VM
得到VIH和VIL之后就可以得到
N
M
H
NM_H
NMH和
N
M
L
NM_L
NML,即高电压噪声容限和低电压噪声容限。
N
M
H
=
V
D
D
−
V
I
H
NM_H=V_{DD}-V_{IH}
NMH=VDD−VIH
N
M
L
=
V
I
L
NM_L=V_{IL}
NML=VIL
最后我们还要求一下g的表达式
k
n
V
D
S
A
T
n
(
V
i
n
−
V
T
n
−
V
D
S
A
T
n
2
)
(
1
+
λ
n
V
o
u
t
)
+
k
p
V
D
S
A
T
p
(
V
i
n
−
V
D
D
−
V
T
p
−
V
D
S
A
T
p
2
)
(
1
+
λ
p
V
o
u
t
−
λ
p
V
D
D
)
=
0
\begin{gathered}k_nV_{DSATn}\bigg(V_{in}-V_{Tn}-\frac{V_{DSATn}}2\bigg)(1+\lambda_nV_{out})+k_pV_{DSATp}\bigg(V_{in}-V_{DD}-V_{Tp}-\frac{V_{DSATp}}2\bigg)(1+\lambda_pV_{out}-\lambda_pV_{DD})=0\end{gathered}
knVDSATn(Vin−VTn−2VDSATn)(1+λnVout)+kpVDSATp(Vin−VDD−VTp−2VDSATp)(1+λpVout−λpVDD)=0
通过对这个反相器的电流表达式求导即可得增益。
即 d V o u t d V i n = − k n V D S A T n ( 1 + λ n V o u t ) + k p V D S A T p ( 1 + λ p V o u t − λ p V D D ) λ n k n V D S A T n ( V i n − V T n − V D S A T n / 2 ) + λ p k p V D S A T p ( V i n − V D D − V T p − V D S A T p / 2 ) \frac{\mathrm{d}V_{out}}{\mathrm{d}V_{in}}=-\frac{k_nV_{DSATn}(1+\lambda_nV_{out})+k_pV_{DSATp}(1+\lambda_pV_{out}-\lambda_pV_{DD})}{\lambda_nk_nV_{DSATn}(V_{in}-V_{Tn}-V_{DSATn}/2)+\lambda_pk_pV_{DSATp}(V_{in}-V_{DD}-V_{Tp}-V_{DSATp}/2)} dVindVout=−λnknVDSATn(Vin−VTn−VDSATn/2)+λpkpVDSATp(Vin−VDD−VTp−VDSATp/2)knVDSATn(1+λnVout)+kpVDSATp(1+λpVout−λpVDD)
忽略某些二次项并令Vin=VM代入上式得到
g
=
−
1
I
D
(
V
M
)
k
n
V
D
S
A
T
n
+
k
p
V
D
S
A
T
p
λ
n
−
λ
p
≈
1
+
r
(
V
M
−
V
T
n
−
V
D
S
A
T
n
/
2
)
(
λ
n
−
λ
p
)
\begin{aligned}g&=-\frac1{I_D(V_M)}\frac{k_nV_{DSATn}+k_pV_{DSATp}}{\lambda_n-\lambda_p}\\&\approx\frac{1+r}{(V_M-V_{Tn}-V_{DSATn}/2)(\lambda_n-\lambda_p)}\end{aligned}
g=−ID(VM)1λn−λpknVDSATn+kpVDSATp≈(VM−VTn−VDSATn/2)(λn−λp)1+r
其中
I
D
(
V
M
)
I_D(V_M)
ID(VM)是Vin=VM时流过反相器的电流。
观察上述的g的表达式可知,这个增益几乎完全取决于工艺参数,特别是沟道长度调制效应。通过改变电源电压和晶体管尺寸产生的影响很小。
在实际例子中,通过上述表达式算出来的g绝对值会比实际偏大,所以实际中噪声容限是要比理论计算小的。关于这段话的论证,可以看原书的例题5.2
5.3.3 再谈稳定性
器件参数的变化
我们之前就讨论过,器件大小的变化对开关阈值变化并不明显,但是为了进一步确认其他工艺参数也不会对CMOS门造成大影响,我们还是进行了如下仿真。
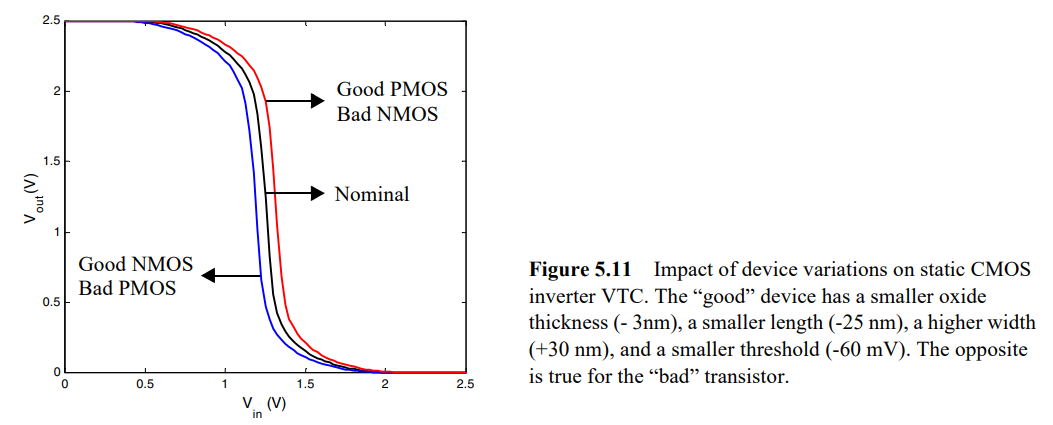
可以发现器件的栅氧厚度,长度,宽度和阈值对VTC曲线变化不是很明显,这是非常好的特性!
降低电源电压
根据这个表达式①
g
=
−
1
I
D
(
V
M
)
k
n
V
D
S
A
T
n
+
k
p
V
D
S
A
T
p
λ
n
−
λ
p
≈
1
+
r
(
V
M
−
V
T
n
−
V
D
S
A
T
n
/
2
)
(
λ
n
−
λ
p
)
\begin{aligned}g&=-\frac1{I_D(V_M)}\frac{k_nV_{DSATn}+k_pV_{DSATp}}{\lambda_n-\lambda_p}\\&\approx\frac{1+r}{(V_M-V_{Tn}-V_{DSATn}/2)(\lambda_n-\lambda_p)}\end{aligned}
g=−ID(VM)1λn−λpknVDSATn+kpVDSATp≈(VM−VTn−VDSATn/2)(λn−λp)1+r和表达式②
V
M
≈
r
V
D
D
1
+
r
V_M\approx\frac{rV_{DD}}{1+r}
VM≈1+rrVDD我们得到一个结论。
如果降低VDD,那么g的绝对值会增大,这肯定是有好处的
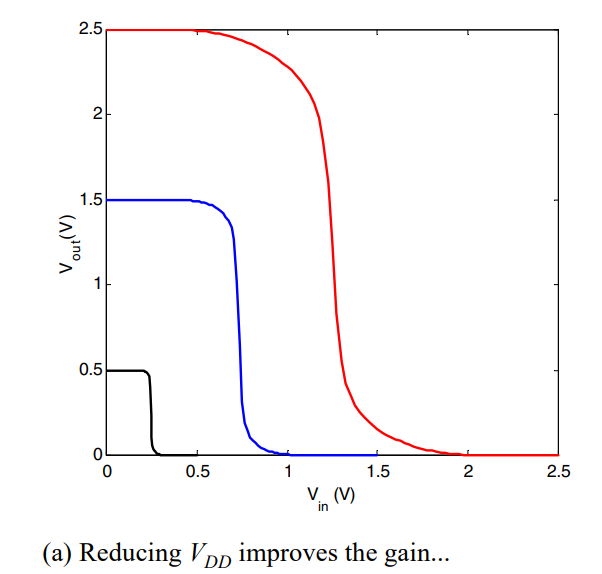
假定阈值电压Vth=0.4V,从这张图可以看出,当VDD>Vth时,减小VDD确确实实能增大过渡区增益。那我们能不能继续降低VDD到Vth以下呢?答案是可以再减小一点,但是也不能太少。那究竟具体能到多少呢?请看下面分析。
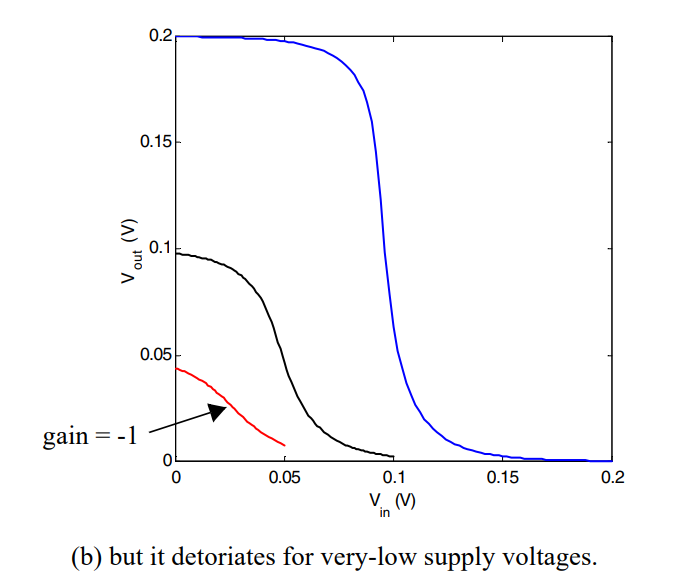
假如我们再降VDD,让其在Vth以下,仍然会存在VTC曲线,这是亚阈值电流的原因,但是由于电流太小,输出变化其实是很慢的。然而我们发现当VDD降到很小的时候,VTC曲线就开始不成样子了,根据理论知识,我们要求电源电压大于两倍的热电势,因为当VDD低于这一个电压的时候,热噪声就很大了,会出问题,写成表达式如下
V D D m i n > 2...4 k T q V_{DDmin}>2...4\frac{kT}q VDDmin>2...4qkT
5.3 CMOS反相器的动态特性
由于CMOS的传播延时与CL负载电容有关,那么减小CL就是关键,既然要减小CL,那我们就要分析CL具体是怎么组成的。
5.3.1 计算电容值

这张图画出的所有电容都会影响Vout的瞬态响应,所以我们把图中的所有电容加起来就是Vout点出的CL。下面讨论CL是我们假定Vin输入的信号上升和下降时间都为0。
5.3.1.1 栅漏电容 C g d 1 , 2 C_{gd1,2} Cgd1,2
密勒效应(Miller effect)是在电子学中,反相放大电路中(反相电路独有!),输入与输出之间的分布电容或寄生电容由于放大器的放大作用,其等效到输入端的电容值会变成1+K倍,等效到输出的电容会变成1+1/K倍,其中K是该级放大电路电压放大倍数的绝对值。所以其中一个栅漏电容等效如下图所示。默认反相器K=-1
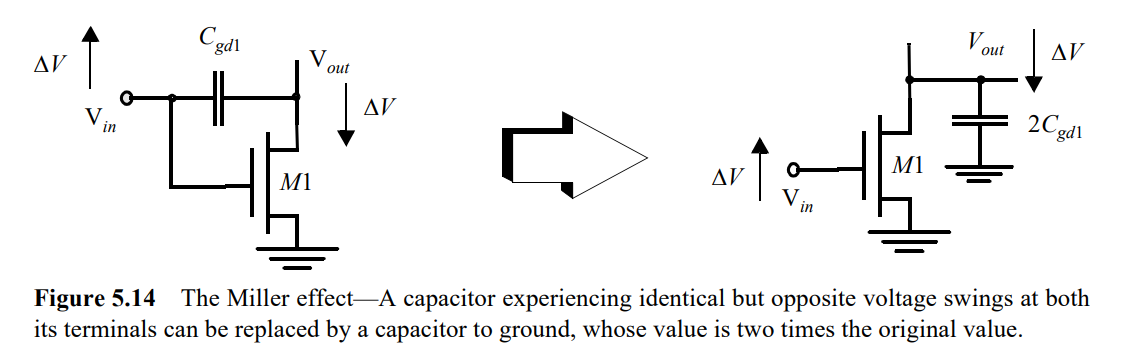
假如Vout一开始是高点平,Vin一开始是低电平,这个时候NMOS处于截止区,这个时候Vin瞬间变成高点平,在这一瞬间NMOS是处于饱和区的,然后Vout开始放电,我们只讨论Vout从VDD放电到1/2 VDD的过程,同时假定1/2VDD>VDD-Vthn,在这个假定下,NMOS在开始的时候是截止区,Vin一变化到高点平到放电结束(Vout=1/2VDD)这个过程,NMOS都处于饱和区。在这个分析下,我们可以得到Cgd的公式如下
C g d n = 2 C G D 0 n W n C_{gdn}=2C_{GD0n}W_n Cgdn=2CGD0nWn,注意这个只是NMOS的Cgd,不包括PMOS的,PMOS和这个类似但是这个公式已经考虑了密勒效应。
5.3.1.2 扩散电容 C d b 1 , 2 C_{db1,2} Cdb1,2
扩散电容来自于漏极和体之间的反偏PN结,之前在讨论MOS器件的时候已经讨论过了,详情见这篇博文超大规模集成电路设计----MOS器件原理(三)
然而这是一个非线性的电容,我们将其线性化如下。
C
e
q
=
K
e
q
C
j
0
C_{eq}=K_{eq}C_{j0}
Ceq=KeqCj0
K
e
q
=
−
ϕ
0
m
(
V
h
i
g
h
−
V
l
o
w
)
(
1
−
m
)
[
(
ϕ
0
−
V
h
i
g
h
)
1
−
m
−
(
ϕ
0
−
V
l
o
w
)
1
−
m
]
K_{eq}=\frac{-\phi_0^m}{(V_{high}-V_{low})(1-m)}[(\phi_0-V_{high})^{1-m}-(\phi_0-V_{low})^{1-m}]
Keq=(Vhigh−Vlow)(1−m)−ϕ0m[(ϕ0−Vhigh)1−m−(ϕ0−Vlow)1−m]
5.3.1.3 连线电容 C w C_{w} Cw
这个电容取决于连线的长度和宽度,还与扇出离驱动门的距离,扇出门的数目有关。
5.3.1.4 扇出的栅电容 C g 3 , 4 C_{g3,4} Cg3,4
假设负载栅电容等于两个负载门栅电容的总和。
C
f
a
n
o
u
t
=
C
g
a
t
e
(
N
M
O
S
)
+
C
g
a
t
e
(
P
M
O
S
)
=
(
C
G
S
O
n
+
C
G
D
O
n
+
W
n
L
n
C
o
x
)
+
(
C
G
S
O
p
+
C
G
D
O
p
+
W
p
L
p
C
o
x
)
\begin{aligned}C_{fanout}&=C_{gate}(\mathrm{NMOS})+C_{gate}(\mathrm{PMOS})\\&=(C_{GSOn}+C_{GDOn}+W_{n}L_{n}C_{ox})+(C_{GSOp}+C_{GDOp}+W_{p}L_{p}C_{ox})\end{aligned}
Cfanout=Cgate(NMOS)+Cgate(PMOS)=(CGSOn+CGDOn+WnLnCox)+(CGSOp+CGDOp+WpLpCox)
这里我们认为
C
g
3
C_{g3}
Cg3和
C
g
4
C_{g4}
Cg4是直接连接到VDD和GND的,并且忽略密勒效应。同时假定一个管子一直是线性的,另一个管子从截止进入饱和状态,这样的话沟道电容一直不变,一直是
W
L
C
o
x
WLC_{ox}
WLCox
5.3.1.5 总的电容 C L C_L CL
C L = ( C g d 1 + C d g 2 ) + ( C d b 1 + C d b 2 ) + ( C g 3 + C g 4 ) + C w C_L=(C_{gd1}+C_{dg2})+(C_{db1}+C_{db2})+(C_{g3}+C_{g4})+C_w CL=(Cgd1+Cdg2)+(Cdb1+Cdb2)+(Cg3+Cg4)+Cw
5.3.1.6 识版图
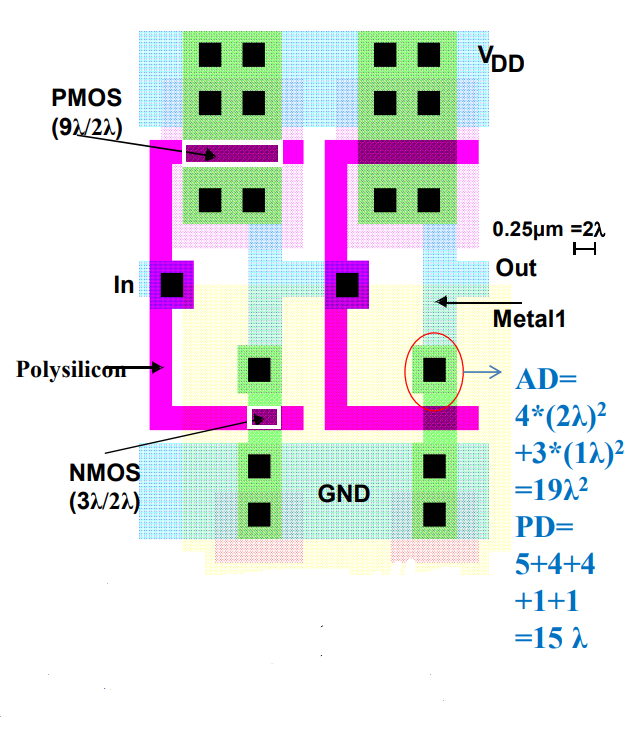
5.3.2 传播延时:一阶分析
简要分析VDD、W/L、CL对 t p t_p tp的影响
t p H L = ln ( 2 ) R e q n C L = 0.69 R e q n C L t p L H = 0.69 R e q p C L t p = t p H L + t p L H 2 = 0.69 C L ( R e q n + R e q p 2 ) \begin{aligned} &t_{pHL}=\ln(2)R_{eqn}C_{L}=0.69R_{eqn}C_{L} \\ &t_{pLH}=0.69R_{eqp}C_{L} \\ &t_{p}=\frac{t_{pHL}+t_{pLH}}{2}=0.69C_{L}\Big(\frac{R_{eqn}+R_{eqp}}{2}\Big) \end{aligned} tpHL=ln(2)ReqnCL=0.69ReqnCLtpLH=0.69ReqpCLtp=2tpHL+tpLH=0.69CL(2Reqn+Reqp)
R e q = 1 V D D / 2 ∫ V D D / 2 V I D S A T ( 1 + λ V ) d V ≈ 3 4 V D D I D S A T ( 1 − 7 9 λ V D D ) w i t h I D S A T = k W L ( ( V D D − V T ) V D S A T − V D S A T 2 2 ) \begin{gathered} R_{eq} =\frac{1}{V_{DD}/2}\int_{V_{DD}/2}\frac{V}{I_{DSAT}(1+\lambda V)}dV\approx\frac{3}{4}\frac{V_{DD}}{I_{DSAT}}\biggl(1-\frac{7}{9}\lambda V_{DD}\biggr) \\ \mathrm{with}\quad I_{DSAT}=k\frac{W}{L}\Big((V_{DD}-V_{T})V_{DSAT}-\frac{V_{DSAT}^{2}}{2}\Big) \end{gathered} Req=VDD/21∫VDD/2IDSAT(1+λV)VdV≈43IDSATVDD(1−97λVDD)withIDSAT=kLW((VDD−VT)VDSAT−2VDSAT2)
综上得到
t
p
H
L
=
0.69
3
4
C
L
V
D
D
I
D
S
A
T
n
=
0.52
C
L
V
D
D
(
W
/
L
)
n
k
n
′
V
D
S
A
T
n
(
V
D
D
−
V
T
n
−
V
D
S
A
T
n
/
2
)
t_{_{pHL}}=0.69\frac{3}{4}\frac{C_{L}V_{DD}}{I_{DSATn}}=0.52\frac{C_{L}V_{DD}}{(W/L)_{n}k'_{n}V_{DSATn}(V_{DD}-V_{Tn}-V_{DSATn}/2)}
tpHL=0.6943IDSATnCLVDD=0.52(W/L)nkn′VDSATn(VDD−VTn−VDSATn/2)CLVDD
如果我们保证
V
D
D
>
>
V
T
n
+
V
D
S
A
T
n
/
2
V_{DD}>>V_{Tn}+V_{DSATn}/2
VDD>>VTn+VDSATn/2
可以得到
t
p
H
L
≈
0.52
C
L
(
W
/
L
)
n
k
n
′
V
D
S
A
T
n
t_{pHL}\approx0.52\frac{C_{L}}{(W/L)_{n}k'_{n}V_{DSATn}}
tpHL≈0.52(W/L)nkn′VDSATnCL
其中KaTeX parse error: Expected 'EOF', got '}' at position 10: V_{DSATn}}̲我们在器件章节讲过,正相关于VGS,而VGS正相关与VDD,所以VDD上升,传播延时降低,下图也表明了这个现象
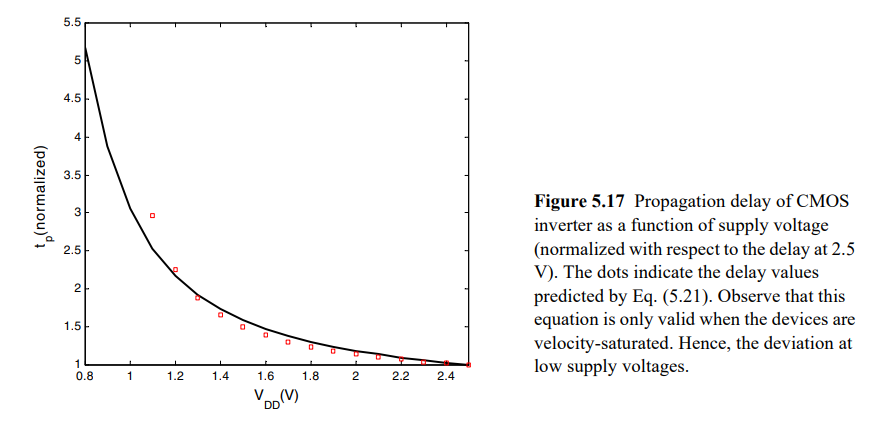
看图可知,当VDD=2VT=0.8V时,延时大大增加,如果是高性能设计,避免这么做。我们前面讲的静态特性中,讲过VDD的最少为两倍热电压,就提过这个时候速度很慢,这张图算是二次验证了这个理论。
其实我们看到这个公式 t p H L ≈ 0.52 C L ( W / L ) n k n ′ V D S A T n t_{pHL}\approx0.52\frac{C_{L}}{(W/L)_{n}k'_{n}V_{DSATn}} tpHL≈0.52(W/L)nkn′VDSATnCL,可以发现CL减小和W/L增大也可以对性能进行提升。
5.3.3 从设计角度考虑传播延时
5.3.3.1 PMOS与NMOS—β参数
考虑两个完全相同的CMOS反相器串联,第一级负载
C
L
=
(
C
d
p
1
+
C
d
n
1
)
+
(
C
g
p
2
+
C
g
n
2
)
+
C
W
C_{L}=(C_{dp1}+C_{dn1})+(C_{gp2}+C_{gn2})+C_{W}
CL=(Cdp1+Cdn1)+(Cgp2+Cgn2)+CW,这里忽略了第一级的栅漏电容。令
β
=
(
W
/
L
)
p
/
(
W
/
L
)
n
\beta=(W/L)_p/(W/L)_n
β=(W/L)p/(W/L)n
则
C
d
p
1
≈
β
C
d
n
1
,
C
g
p
2
≈
β
′
C
g
n
2
C_{dp1}\approx\beta C_{dn1},C_{gp2}\approx\beta^{\prime}C_{gn2}
Cdp1≈βCdn1,Cgp2≈β′Cgn2
由此可以推出传播延时
t
p
=
0.69
2
(
(
1
+
β
)
(
C
d
n
1
+
C
g
n
2
)
+
C
W
)
(
R
e
q
n
+
R
e
q
p
β
)
=
0.345
(
(
1
+
β
)
(
C
d
n
1
+
C
g
n
2
)
+
C
W
)
R
e
q
n
(
1
+
r
β
)
\begin{aligned}t_{p}&=\frac{0.69}{2}((1+\beta)(C_{dn1}+C_{gn2})+C_{W})\Big(R_{eqn}+\frac{R_{eqp}}{\beta}\Big)\\\\&=0.345((1+\beta)(C_{dn1}+C_{gn2})+C_{W})R_{eqn\Big(1+\frac{r}{\beta}\Big)}\end{aligned}
tp=20.69((1+β)(Cdn1+Cgn2)+CW)(Reqn+βReqp)=0.345((1+β)(Cdn1+Cgn2)+CW)Reqn(1+βr)
令
∂
t
p
∂
β
=
0
\frac{\partial t_p}{\partial\mathbf{\beta}}=0
∂β∂tp=0可得
β
o
p
t
=
r
(
1
+
C
w
C
d
n
1
+
C
g
n
2
)
\beta_{opt}=\sqrt{r\Big(1+\frac{C_w}{C_{dn1}+C_{gn2}}\Big)}
βopt=r(1+Cdn1+Cgn2Cw)
这个式子告诉我们导线电容可以忽略时,
C
d
n
l
+
C
g
n
2
>
>
C
W
C_{dnl}+C_{gn2}>>C_{W}
Cdnl+Cgn2>>CW,最佳的
β
=
r
β=\sqrt r
β=r,如果导线电容较大,
β
>
r
β>\sqrt r
β>r
我们知道,当β=Reqp/Reqn=31/13=2.4时,PMOS和NMOS的等效电阻就一样大了,那么上升延时和下降延时就相等。
当
β
=
r
β=\sqrt r
β=r时,(其中
r
=
R
e
q
p
/
R
e
q
n
r=Reqp/Reqn
r=Reqp/Reqn),这个时候时间是最短的。
我们之前还学过,由开关阈值VM=1/2VDD所导出的β=3.5
开关阈值公式如下
(
W
/
L
)
p
(
W
/
L
)
n
=
k
n
′
V
D
S
A
T
n
(
V
M
−
V
T
n
−
V
D
S
A
T
n
/
2
)
k
p
′
V
D
S
A
T
p
(
V
D
D
−
V
M
+
V
T
p
+
V
D
S
A
T
p
/
2
)
\frac{(W/L)_p}{(W/L)_n}=\frac{k'_nV_{DSATn}(V_M-V_{Tn}-V_{DSATn}/2)}{k'_pV_{DSATp}(V_{DD}-V_M+V_{Tp}+V_{DSATp}/2)}
(W/L)n(W/L)p=kp′VDSATp(VDD−VM+VTp+VDSATp/2)kn′VDSATn(VM−VTn−VDSATn/2)
5.3.3.2 超大负载时单个反相器尺寸确定
上面讨论的β公式是建立在两个反相器级联的情况下,这个时候负载并不是很大,但是如果负载很大我们怎么办呢?接下来请看。
C
ˉ
L
=
C
i
n
t
+
C
e
x
t
.
\bar{C}_{L}=C_{int}+C_{ext}.
CˉL=Cint+Cext.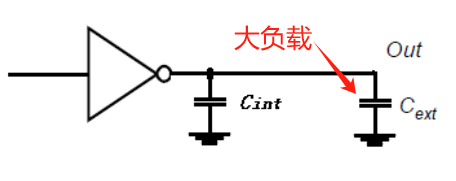
C
L
=
C
i
n
t
+
C
e
x
t
.
C_{L}=C_{int}+C_{ext}.
CL=Cint+Cext.我们要注意负载电容分成自载电容(本征输出电容)和外部负载电容。
t p = 0.69 R e q ( C i n t + C e x t ) = 0.69 R e q C i n t ( 1 + C e x t / C i n t ) = t p 0 ( 1 + C e x t / C i n t ) \begin{aligned}t_p&=0.69R_{eq}(C_{int}+C_{ext})\\&=0.69R_{eq}C_{int}(1+C_{ext}/C_{int})=t_{p0}(1+C_{ext}/C_{int})\end{aligned} tp=0.69Req(Cint+Cext)=0.69ReqCint(1+Cext/Cint)=tp0(1+Cext/Cint)
t p 0 = 0.69 R e q C i n t t_{p0}=0.69R_{eq}C_{int} tp0=0.69ReqCint是反相器空载延时,也叫本征延时。
定义尺寸系数S,S表示当前门与参考门大小的比值。
因此
C
i
n
t
=
S
C
i
r
e
f
C_{int}=SC_{iref}
Cint=SCiref和
R
e
q
=
R
r
e
f
/
S
R_{eq}=R_{ref}/S
Req=Rref/S
所以 t p = t p 0 ( 1 + C e x t S C i r e f ) t_{p}=t_{p0}\Big(1+\frac{C_{ext}}{SC_{iref}}\Big) tp=tp0(1+SCirefCext)
由以上式子和假设可以得到如下特性:
- 假设参考门的电阻为 R e q 0 R_{eq0} Req0,本征电容为 C i n t 0 C_{int0} Cint0,则尺寸系数为S的门 t p 0 = 0.69 1 S R e q S C i n t = t p 0 = 0.69 R e q 0 C i n t 0 t_{p0}=0.69\frac{1}{S}R_{eq}SC_{int}=t_{p0}=0.69R_{eq0}C_{int0} tp0=0.69S1ReqSCint=tp0=0.69Req0Cint0,说明反相器的本征延时与尺寸无关。
- S无穷大可以改善性能。
5.3.3.2 超大负载时反相器链尺寸、级数确定
显然我们是不能让S无限大的。那么对于大负载我们该怎么办呢?最好的答案就是反相器链!
C
i
n
t
=
γ
C
g
C_{\mathrm{~int}}=\gamma C_{g}
C int=γCg
对于大多数工艺γ=1。
t
p
=
0.69
R
e
q
(
C
i
n
t
+
C
e
x
t
)
=
0.69
R
e
q
C
i
n
t
(
1
+
C
e
x
t
/
C
i
n
t
)
=
t
p
0
(
1
+
C
e
x
t
/
C
i
n
t
)
=
t
p
0
(
1
+
C
e
x
t
γ
C
g
)
=
t
p
0
(
1
+
f
/
γ
)
\begin{aligned}t_p&=0.69R_{eq}(C_{int}+C_{ext})\\&=0.69R_{eq}C_{int}(1+C_{ext}/C_{int})=t_{p0}(1+C_{ext}/C_{int})=t_{p0}\bigg(1+\frac{C_{ext}}{\gamma C_{g}}\bigg)=t_{p0}(1+f/\gamma)\end{aligned}
tp=0.69Req(Cint+Cext)=0.69ReqCint(1+Cext/Cint)=tp0(1+Cext/Cint)=tp0(1+γCgCext)=tp0(1+f/γ)
f = C e x t / C g f=C_{ext}/C_g f=Cext/Cg其中 f f f被称为有效扇出(effective fanout),只取决于外部负载和输入电容

现有如上图N级反相器链,确定其级数N和有效扇出
f
f
f使其传播延时最小。
t
p
,
j
=
t
p
0
(
1
+
C
g
,
j
+
1
γ
C
g
,
j
)
=
t
p
0
(
1
+
f
j
/
γ
)
\begin{aligned}t_{p,j}&=t_{p0}\bigg(1+\frac{C_{g,j+1}}{\gamma C_{g,j}}\bigg)=t_{p0}(1+f_j/\gamma)\end{aligned}
tp,j=tp0(1+γCg,jCg,j+1)=tp0(1+fj/γ)
t p = ∑ j = 1 N t p , j = t p 0 ∑ j = 1 N ( 1 + C g , j + 1 γ C g , j ) t_p~=~\sum_{j~=~1}^Nt_{p,j}~=~t_{p0}\sum_{j~=~1}^N\left(1+\frac{C_{g,j+1}}{\gamma C_{g,j}}\right) tp = ∑j = 1Ntp,j = tp0∑j = 1N(1+γCg,jCg,j+1)其中 C g , N + 1 = C L C_{g,N+1}~=~C_L Cg,N+1 = CL
对这个式子求导并令其等于0可得 C g , j = C g , j − 1 C g , j + 1 C_{g,j}=\sqrt{C_{g,j-1}C_{g,j+1}} Cg,j=Cg,j−1Cg,j+1
所以有效扇出
f
=
C
L
/
C
g
,
1
N
=
F
N
f=\sqrt[N]{C_L/C_{g,1}}=\sqrt[N]{F}
f=NCL/Cg,1=NF其中
F
F
F是总有效扇出
总的延时
t
p
=
N
t
p
0
(
1
+
F
N
/
γ
)
\begin{aligned}t_p=Nt_{p0}(1+\sqrt[N]{F}/\gamma)\end{aligned}
tp=Ntp0(1+NF/γ)
对上面这个总延时两边对N求导并令导数为0可得
γ
+
F
N
−
F
N
ln
F
N
=
0
\gamma+\sqrt[N]{F}-\frac{\sqrt[N]{F}\ln F}N=0
γ+NF−NNFlnF=0
或者说
f
=
−
e
(
1
+
γ
/
f
)
f=-e^{(1+\gamma/f)}
f=−e(1+γ/f)(记住这个式子),如果γ=0,
f
=
e
f=e
f=e,但是如果γ=1只能画图解,我们直接记住这个值,当γ=1时,
f
=
3.6
f=3.6
f=3.6。
反相器链例题
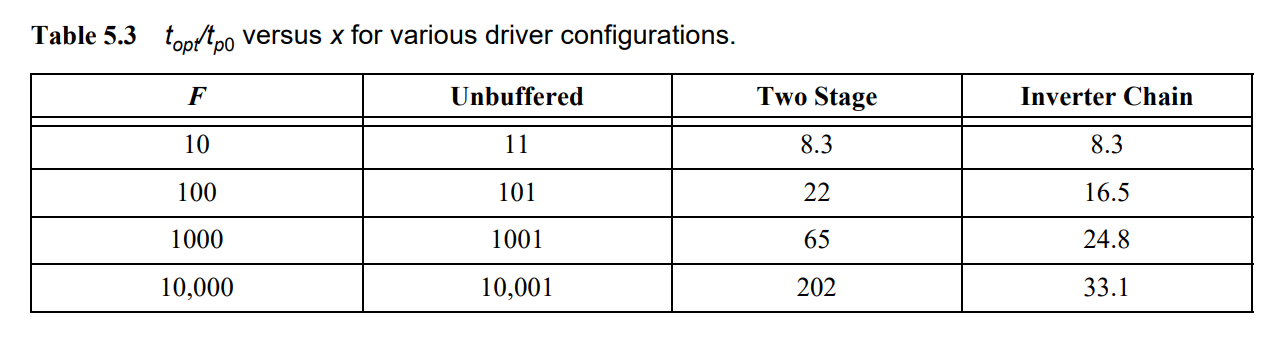
上表是γ=1的情况下
t
o
p
t
/
t
p
0
t_{opt}/t_{p0}
topt/tp0随总有效扇出F的表格。
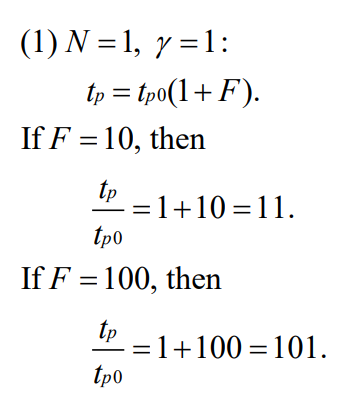
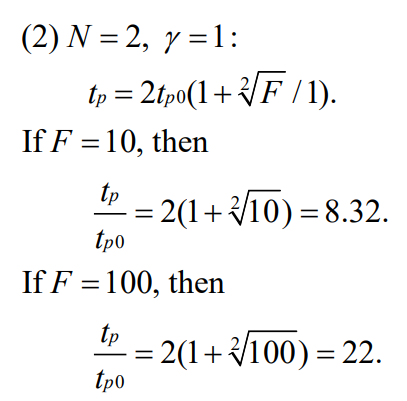
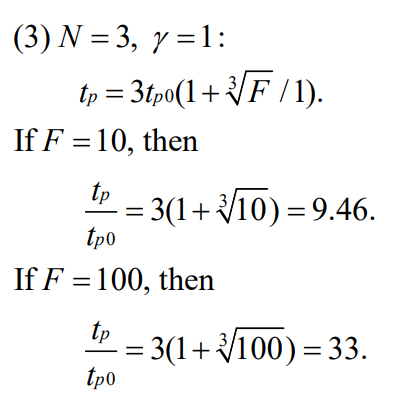

5.3.3.3 输入信号上升下降时间对传播延时的影响
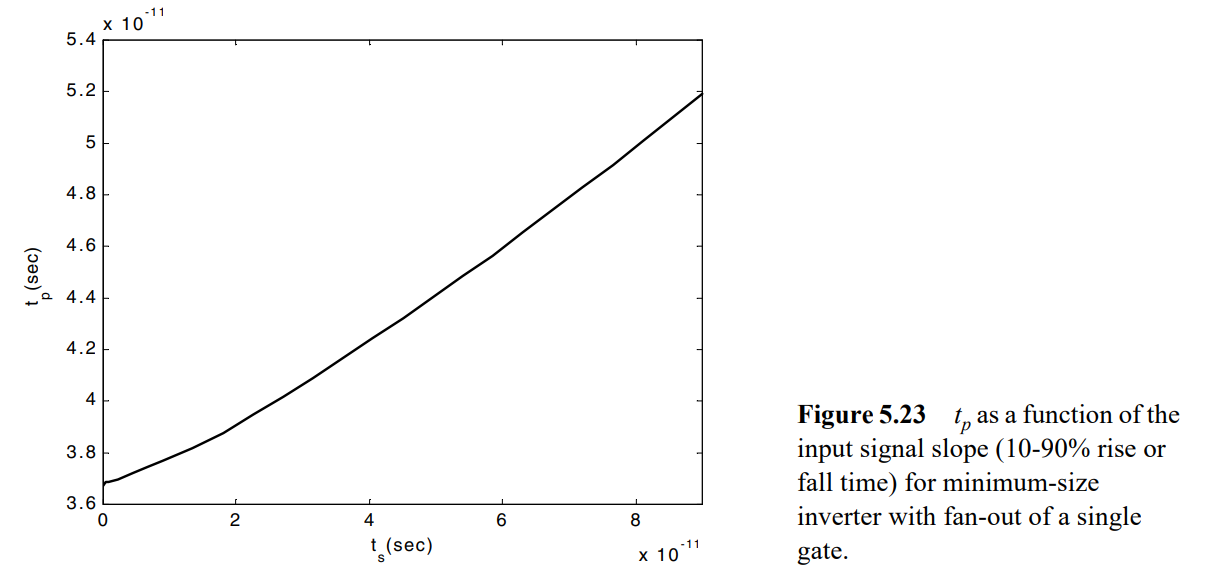
输入变化越慢,PMOS和NMOS同时导通时间越长,影响充电电流,导致传播延时增加。
5.3.3.4 存在互连线时的延时
t p = 0.69 R d r C i n t + ( 0.69 R d r + 0.38 R w ) C w + 0.69 ( R d r + R w ) C f a n = 0.69 R d r ( C i n t + C f a n ) + 0.69 ( R d r c w + r w C f a n ) L + 0.38 r w c w L 2 \begin{array}{rcl}t_p&=&0.69R_{dr}C_{int}+(0.69R_{dr}+0.38R_w)C_w+0.69(R_{dr}+R_w)C_{fan}\\\\&=&0.69R_{dr}(C_{int}+C_{fan})+0.69(R_{dr}c_w+r_wC_{fan})L+0.38r_wc_wL^2\end{array} tp==0.69RdrCint+(0.69Rdr+0.38Rw)Cw+0.69(Rdr+Rw)Cfan0.69Rdr(Cint+Cfan)+0.69(Rdrcw+rwCfan)L+0.38rwcwL2
5.4 功耗、能量和能量延时
5.4.1 动态功耗
5.4.1.1 充放电电容引起的功耗
负载电容从0充电到VDD,电源能量一半被PMOS消耗,一半存在负载电容中,负载电容从VDD放电到0,全部能量被NMOS消耗。
E
V
D
D
=
∫
0
∞
i
V
D
D
(
t
)
V
D
D
d
t
=
V
D
D
∫
0
∞
C
L
d
ν
o
u
t
d
t
d
t
=
C
L
V
D
D
∫
0
V
D
D
d
ν
o
u
t
=
C
L
V
D
D
2
E_{VDD}=\int\limits_{0}^{\infty}i_{VDD}(t)V_{DD}dt=V_{DD}\int\limits_{0}^{\infty}C_{L}\frac{d\nu_{out}}{dt}dt=C_{L}V_{DD}\int\limits_{0}^{V_{DD}}d\nu_{out}=C_{L}V_{DD}^{2}
EVDD=0∫∞iVDD(t)VDDdt=VDD0∫∞CLdtdνoutdt=CLVDD0∫VDDdνout=CLVDD2
和 E C = ∫ 0 ∞ i V D D ( t ) ν o u t d t = ∫ 0 ∞ C L d ν o u t d t ν o u t d t = C L ∫ 0 V D D ν o u t d ν o u t = C L V D D 2 E_C=\int_0^\infty i_{VDD}(t)\nu_{out}dt=\int_0^\infty C_L\frac{d\nu_{out}}{dt}\nu_{out}dt=C_L\int_0^{V_{DD}}\nu_{out}d\nu_{out}=\frac{C_LV_{DD}}{2} EC=∫0∞iVDD(t)νoutdt=∫0∞CLdtdνoutνoutdt=CL∫0VDDνoutdνout=2CLVDD
观察上面的式子我们可以发现,功耗和PMOS、NMOS的尺寸无关(即它们的电阻)。假定一个开关周期是输出从低到高和从高到低两个过程,那么这个过程消耗的能量为
C
L
V
D
D
2
C_{L}{V_{DD}}^{2}
CLVDD2。如果这个门的通断频率为
f
0
→
1
f_{0\rightarrow1}
f0→1,则这个们的功率为
P
d
y
n
=
C
L
V
D
D
2
f
0
→
1
P_{dyn}=C_LV_{DD}^2f_{0\to1}
Pdyn=CLVDD2f0→1
5.4.1.2 直流通路引起的功耗
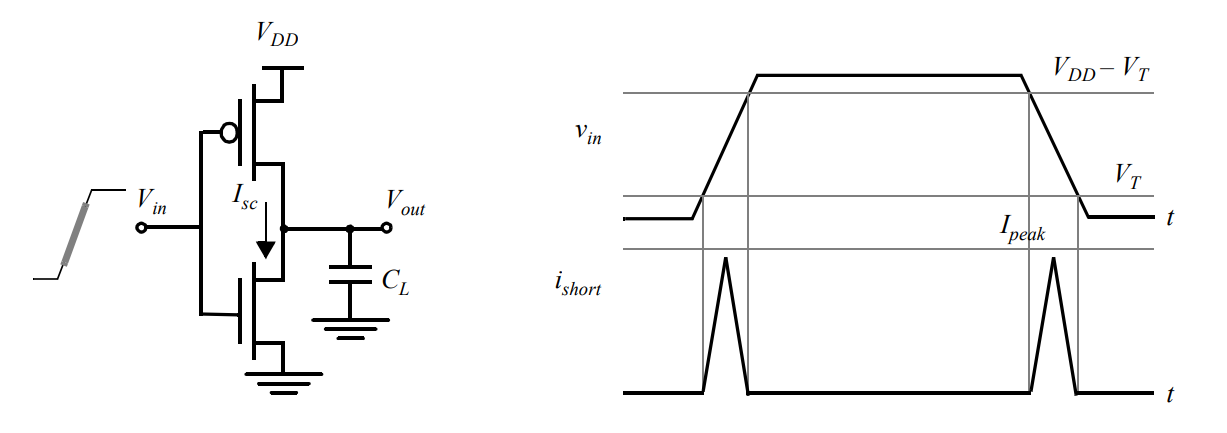
在输入的中间部分两个门都导通,产生了VDD到GND的电流,造成功耗。
5.4.2 静态功耗
漏源与衬底之间的漏电
漏源与衬底之间存在反偏二极管,会漏电。
亚阈值电流
VGS=0=时仍然存在亚阈值电流,且Vth越低,亚阈值电流越大。
5.4.3 总功耗
P t o t = P d y n + P d p + P s t a t = ( C L V D D 2 + V D D I p e a k t s ) f 0 → 1 + V D D I l e a k P_{tot}=P_{dyn}+P_{dp}+P_{stat}=(C_{L}V_{DD}^{2}+V_{DD}I_{peak}t_{s})f_{0\to1}+V_{DD}I_{leak} Ptot=Pdyn+Pdp+Pstat=(CLVDD2+VDDIpeakts)f0→1+VDDIleak



![[CAD]接下来导出一张高清大图](https://img-blog.csdnimg.cn/direct/b33e3bba0fb848b28b8b1a98482cdbbc.png)



![[组合数学]LeetCode:2954:统计感冒序列的数目](https://img-blog.csdnimg.cn/f95ddae62a4e43a68295601c723f92fb.gif#pic_center)