Description

给出一个图的邻接矩阵，再给出指定顶点v0，求顶点v0到其他顶点的最短路径

Input

第一行输入t，表示有t个测试实例

第二行输入n，表示第1个图有n个结点

第三行起，每行输入邻接矩阵的一行，以此类推输入n行

第i个结点与其他结点如果相连则为1，无连接则为0，数据之间用空格隔开

第四行输入v0，表示求v0到其他顶点的最短路径距离

以此类推输入下一个示例

Output

每行输出v0到某个顶点的最短距离和最短路径

每行格式：v0编号-其他顶点编号—-[最短路径]，具体请参考示范数据

Sample

#0

Input

Copy

1
5
0 5 0 7 15
0 0 5 0 0
0 0 0 0 1
0 0 2 0 0
0 0 0 0 0
0

Output

Copy

0-1-5----[0 1 ]
0-2-9----[0 3 2 ]
0-3-7----[0 3 ]
0-4-10----[0 3 2 4 ]

dijkstra求单源最短路径：

可以先参考这篇文章，单纯的dijkstra算法求最短距离，还不用记录路径

        tips：本题要记录最短路径所经过的点

以起点 A 通往前一个点 B 的最短路径+前一个点 B 到下一个点 C 的路径与 现有的A通到C的路径距离相比较求一个最短的路劲。（这里可能不是太理解，请往下看）
首先先知道一个算法里面一个重要的东西 dis[] 数组，他的意思是起点到终点的距离
设起点为 0 
dis[0],起点 0 到 0 的最短距离
dis[1],起点 0 到 1 的最短距离
dis[2],起点 0 到 2 的最短距离

这里与开头说的联系；
假设 0 到 2 存在一条路距离为10 ，0 到 1 存在一条路距离为2 ，1到2存在一条路距离为3

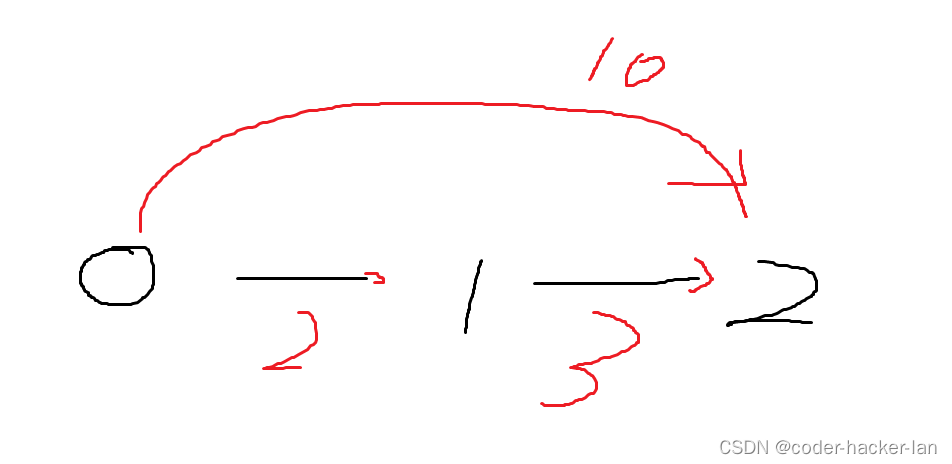
dis[0]=0
dis[1]=2

此时 0 到 1 的路径是 0-1
然后最开始以 2 为前一个出发点，那到达  2  的最短距离已知的是不是10,dis[2]=10

此时 0 到 2 的路径是 0-2
然后 1 为中转点到达 2 的时候，到达2的距离是不是 到达 1 的距离+ 1 到 2的距离dis[1]+1->2=5
此时dis[1]+3<dis[2]=10
所以dis[2]更新为dis[2]=dis[1]+3

此时路径我们发现 0-2 走的路径比 0-1-2 走的长，所以我们就更新路径
所以 0 到 2 的最短路径为 0-1-2

路径：

起点 0 到 1，最短路径就是 0-1

起点 0 到 2，最短路径就是 0-1-2
起初我们记录的 0 到 2的路径是 0-2，但是我们发现走 0-1-2这条路更近，所以取而代之 

样例（自己出的样例跑一遍）

tips:这里我们记录start到dis[i]的最短路径是不包括i本身的
例如：A到C的最短路径是A-B-C，那我们记录的就只有A-B

dis[A]=无穷大 dis[B]=无穷大 dis[C]=无穷大，dis[D]=无穷大
本题设置A为起点
图如下：

令dis[]都为无穷大

令起点到自己为0，因为自己到自己距离为0嘛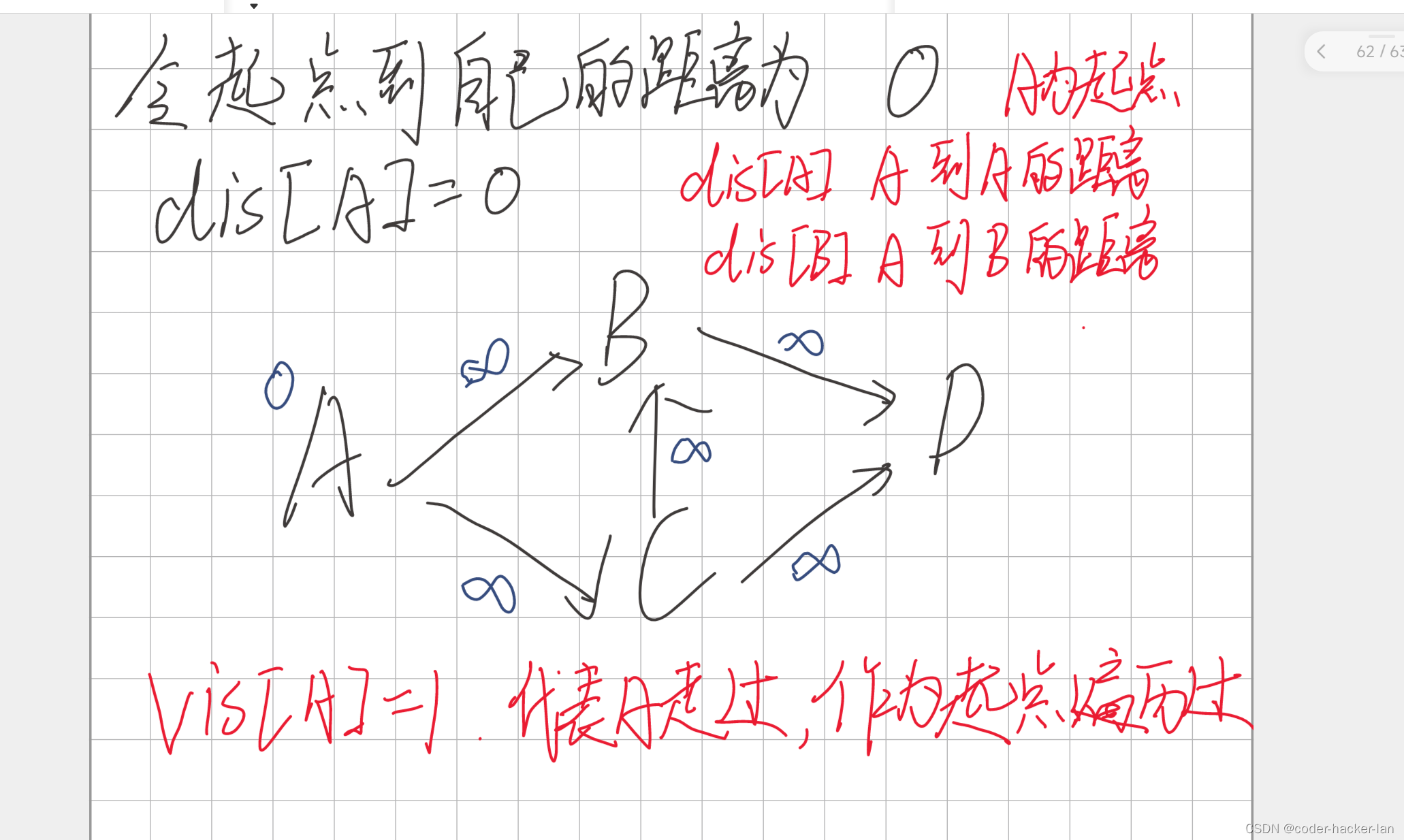

然后dis[]数组中dis[A]是最小的，且没有被作为中转点走过，所以设A为中转点，然后遍历A可以到达的边。这里可以理解为A-A(中转点)-目标点
A可以到达B，C两点，且A到B，C的距离小于无穷大，所以更新起点A到B，C的最短距离为
dis[B]=2,dis[C]=3

此时A到B的最短路径为A
此时A到C的最短路径为A

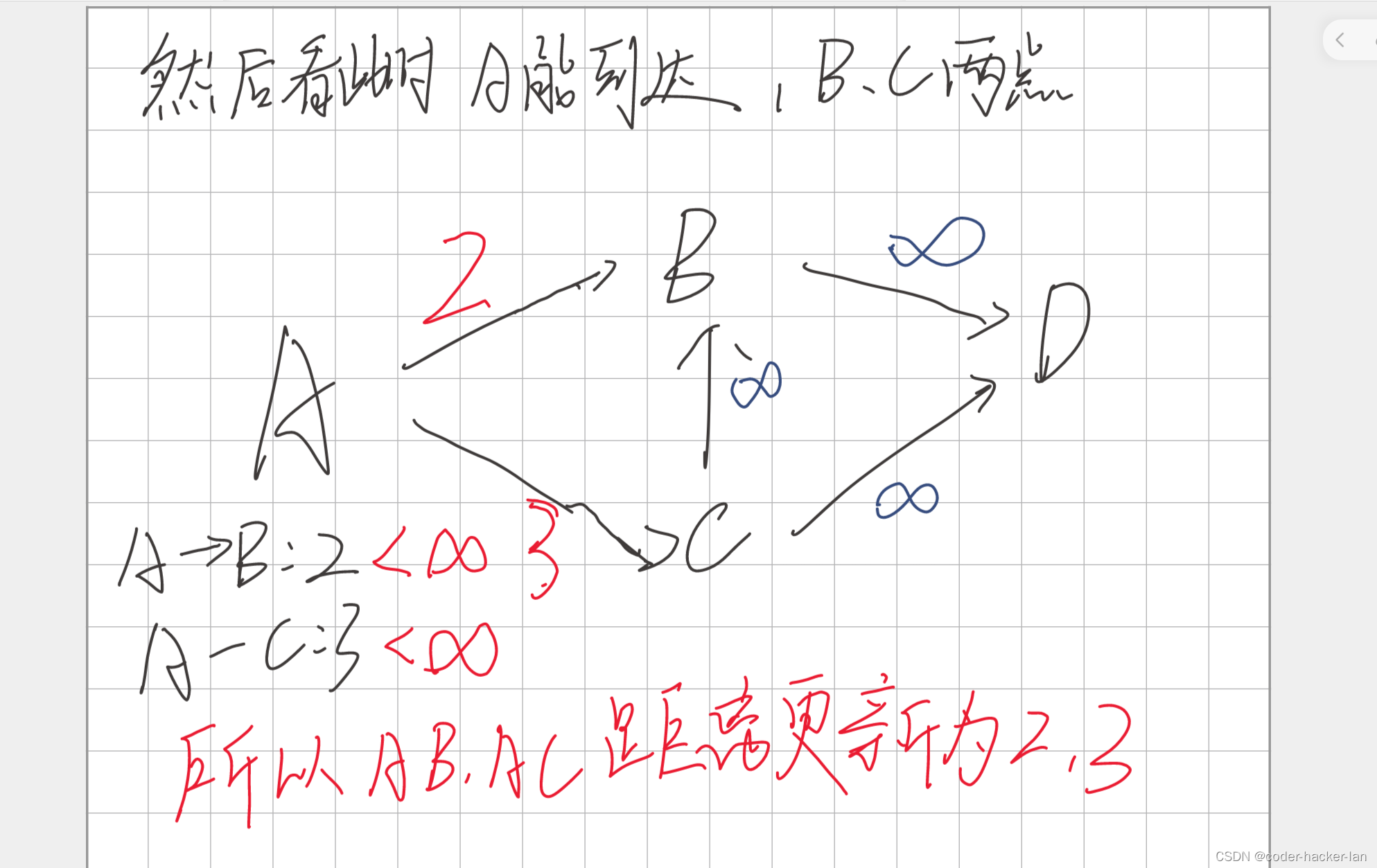
✔的意思是这个点已经被作为中转点走过了

然后找未被作为起始点且起点到他的距离最短，找到B，因为dis[B]=2,dis[C]=3,dis[A]=0但是A已经作为中转点走过了。
B可以到达D点，
起初dis[D]=无穷大，意思为A到D的最短距离为无穷
现在D的路径有从B到D，他的距离为起点A到达B的最短距离+BD路径的距离
dis[B]+BD=12<无穷大
所以dis[D]=12

此时A到D的最短路径为A-B

然后继续重复步骤
此时没有被走过的点是C，D.dis[C]=3,dis[D]=12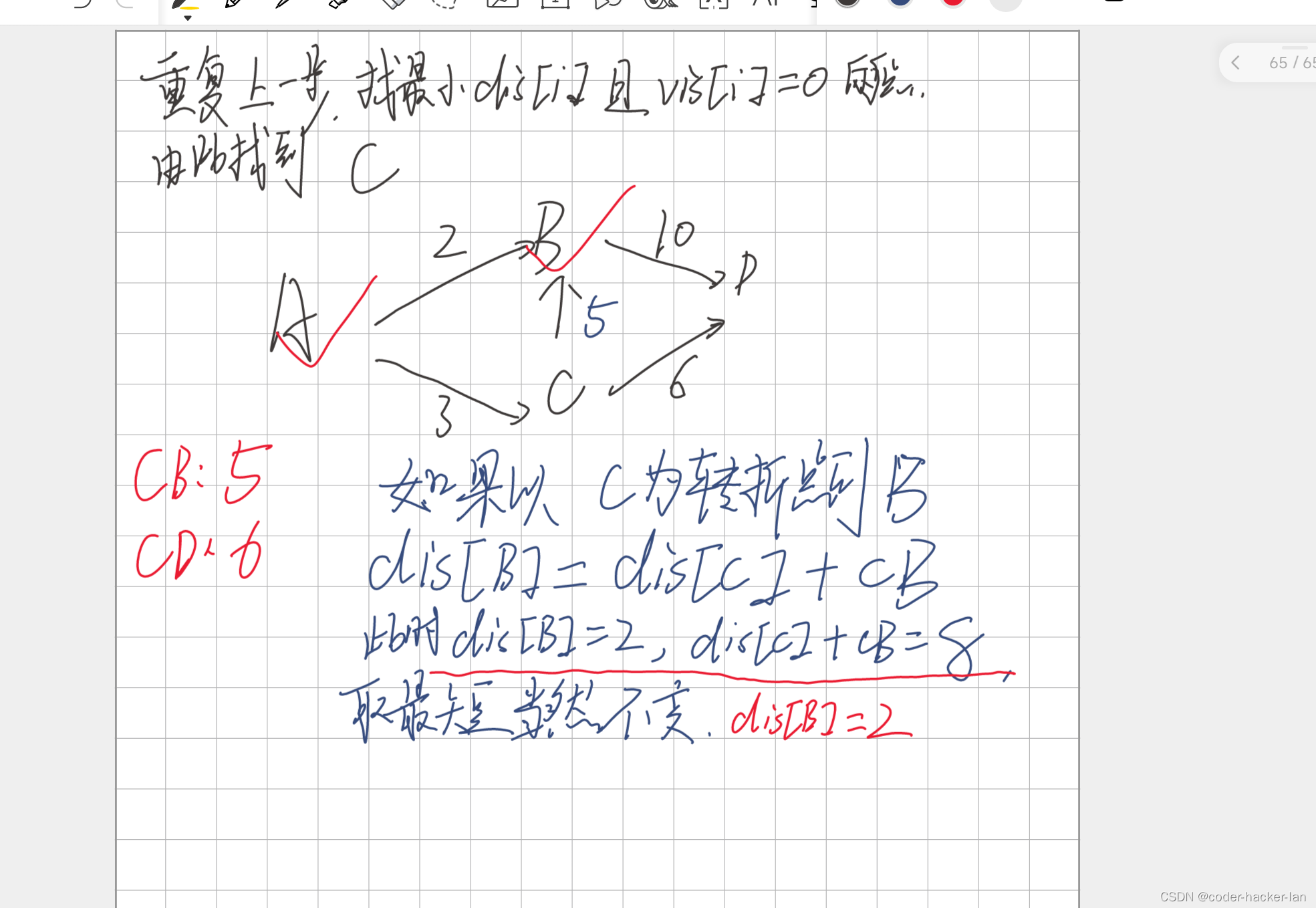
1.C可以到达B
起点A到C的最短距离+CB为B的新一条路距离>dis[B]的前一个路径，即起点A到B的最短路径
dis[C]+CB=8 > dis[B]=2
所以不用更新dis[B]
2.C可以到达D
起点A到D的最短距离+CD为D的新一条路距离<dis[D]的前一个路径，即起点A到D的最短路径
dis[C]+CD=9 > dis[B]=12
所以需要更新起点A到D的最短距离dis[D]=9

此时A到D的路径 A-B的长度大于走A-C的长度
所以更新D的路径为A-C

tips:更新的方法是我们前面已经保存了A到C的路径（不包括C自己），就是路径A，那我们是不是在路径A里面加入要走的C就可以了，就是A-C

最后以D为中转点走，即A到D的最短路径 出发去别的点，但是已经没有D可以到达的点了，所以就结束了

最后得到起点A到别的点的距离
dis[A]=0
dis[B]=2
dis[C]=3
dis[D]=9

最后我们start到各点的最短路径是：

B:A
C:A
D:A-C

最后我们输出实际路径的时候输出完路径再输出终点本身就好了

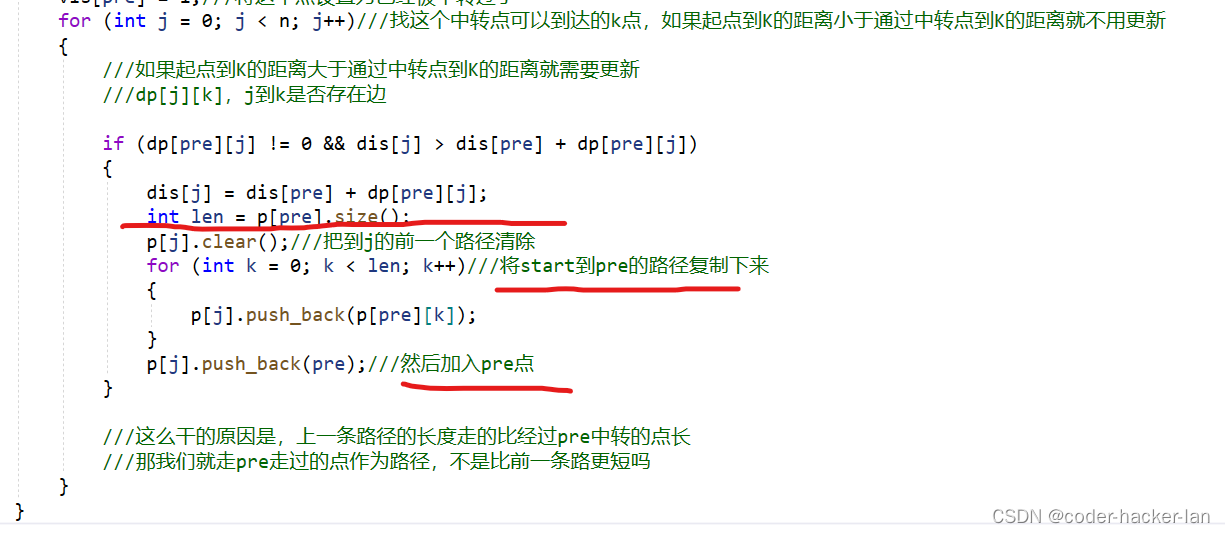
更新路径的写法：

为什么要清除之前的路径呢。

就比如 A-B-C-D要走10m
但是     A-E-F-D要走5m
那你的最短路径是不是从A到C的最短路径+D变成A到E的最短路径+D
那就把A到C的路径删掉，然后换成A到F的最短路径然后+D

tips：本人写法的最短路径是不包括其本身的
所以A到C的最短路径就是A-B，A到F的最短路径是A-E
所以A到D更新前的路径是A-B-C
更新后的是A到F的最短路径A-E加上F，就是A-E-F

enmmm，意思是到end之前最短路径所经过的点，就是不包括end。
那我求end的最短路径是不是end-1之前最短路径所经过的点加end-1这个点

具体代码实现：

#include <iostream>
#include <vector>
#include <algorithm>
#include <string.h>
using namespace std;
int t, n, start;
const int maxn = 2e3 + 10;
int dp[maxn][maxn];//建立的邻接矩阵数组
vector<int>p[maxn];///二维动态数组，记录p[i],起点start到i所需要经过的路径
int vis[maxn];///判断这个点是否有被中转过
int dis[maxn];///dis[i]，表示起点start到终点i的最小距离
void irit()
{
    for (int i = 0; i < n; i++)
    {
        vis[i] = 0;///初始化都没有被作为中转点过
        dis[i] = 0x3f3f3f;///初始化全都是无穷大，start到i的最短距离为无穷大
    }
}
void dijkstra()
{
    dis[start] = 0;///start到start自己的最短距离是0
    for (int i = 0; i < n; i++)///  总共需要n个中转点，次数也是n就够了
    {
        int minm = 0x3f3f3f, pre = 0;///
        for (int j = 0; j < n; j++)///遍历所有dis[],找最小距离的点且没有被作为中转点走过的点
        {
            //vis[k]=0即没有被作为中转点，dis[k]即比较dis距离找距离最小的点
            if (!vis[j] && dis[j] < minm)
            {
                minm = dis[j];//更新最短距离
                pre = j;//找距离最小的点
            }
        }
        vis[pre] = 1;///将这个点设置为已经被中转过了
        for (int j = 0; j < n; j++)///找这个中转点可以到达的k点，如果起点到K的距离小于通过中转点到K的距离就不用更新
        {
            ///如果起点到K的距离大于通过中转点到K的距离就需要更新
            ///dp[j][k]，j到k是否存在边
       
            if (dp[pre][j] != 0 && dis[j] > dis[pre] + dp[pre][j])
            {
                dis[j] = dis[pre] + dp[pre][j];
                int len = p[pre].size();
                p[j].clear();///把到j的前一个路径清除
                for (int k = 0; k < len; k++)///将start到pre的路径复制下来
                {
                    p[j].push_back(p[pre][k]);
                }
                p[j].push_back(pre);///然后加入pre点
            }

            ///这么干的原因是，上一条路径的长度走的比经过pre中转的点长
            ///那我们就走pre走过的点作为路径，不是比前一条路更短吗
        }
    }
}
int main()
{
    cin >> t;
    while (t--)
    {
        cin >> n;
        irit();
        memset(dp, 0, sizeof(dp));
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
            {
                cin >> dp[i][j];//构建邻接矩阵
            }
        }
        cin >> start;///输入起点
        dijkstra();
        for (int i = 0; i < n; i++)
        {
            if (i == start)
                continue;
            cout << start << "-" << i << "-" << dis[i] << "----";
            cout << "[";
            int len = p[i].size();
            for (int j = 0; j < len; j++)///输出到j所走过最短路径的点，这个点是不包括他自身的
            {
                cout << p[i][j] << " ";
            }
            cout << i << " ]" << endl;///输出j自身
        }
    }
    return 0;
}

---

就写到这吧，跟我的追星dijkstra追星还是不说一模一样但也十有八九
原理其实是一样的，但是重要的是掌握我的路径数组的意思，是不包括最后终点自身的

幸苦大家看这么多字了！

夜深了，晚安各位！！！！(￣o￣) . z Z