系列综述:
💞目的:本系列是个人整理为了秋招面试的,整理期间苛求每个知识点,平衡理解简易度与深入程度。
🥰来源:材料主要源于【CodeTopHot200】进行的,每个知识点的修正和深入主要参考各平台大佬的文章,其中也可能含有少量的个人实验自证,所有代码均优先参考最佳性能。
🤭结语:如果有帮到你的地方,就点个赞和关注一下呗,谢谢🎈🎄🌷!!!
🌈【C++】秋招&实习面经汇总篇
文章目录
- 二叉树的构建
- 基础知识
- 654. 构建二叉树*
- 相关题目
- 105. 从前序与中序遍历序列构造二叉树
- 106. 从中序与后序遍历序列构造二叉树
- 二叉搜索树(考察较少,留后处理)
- 基础知识
- 相关题目
- 98. 验证二叉搜索树
- 530. 二叉搜索树的最小绝对差
- 236. 二叉树的最近公共祖先
- 235. 二叉搜索树的最近公共祖先
- 450. 删除二叉搜索树中的节点
- 669. 修剪二叉搜索树
- 108. 将有序数组转换为二叉搜索树
- 669. 修剪二叉搜索树
- 参考博客
😊点此到文末惊喜↩︎
二叉树的构建
基础知识
654. 构建二叉树*
- 654. 最大二叉树
- 通过始末位置指示容器范围,避免每次调用的vector创建开销
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
auto self = [&](auto &&self, int left, int right)->TreeNode*{
// 递归出口
if (left > right) return nullptr;
// 如何划分:查找区间中的最大根节点
int max_pos = left;
for (int i = left+1; i <= right; ++i) {
if (nums[i] > nums[max_pos])
max_pos = i;
}
// 建立根节点,左递归,右递归
TreeNode *root = new TreeNode(nums[max_pos]);
root->left = self(self, left, max_pos-1);
root->right = self(self, max_pos+1, right);
// 返回根节点
return root;
};
TreeNode *root = self(self, 0, nums.size()-1);
return root;
}
相关题目
105. 从前序与中序遍历序列构造二叉树
- 105. 从前序与中序遍历序列构造二叉树
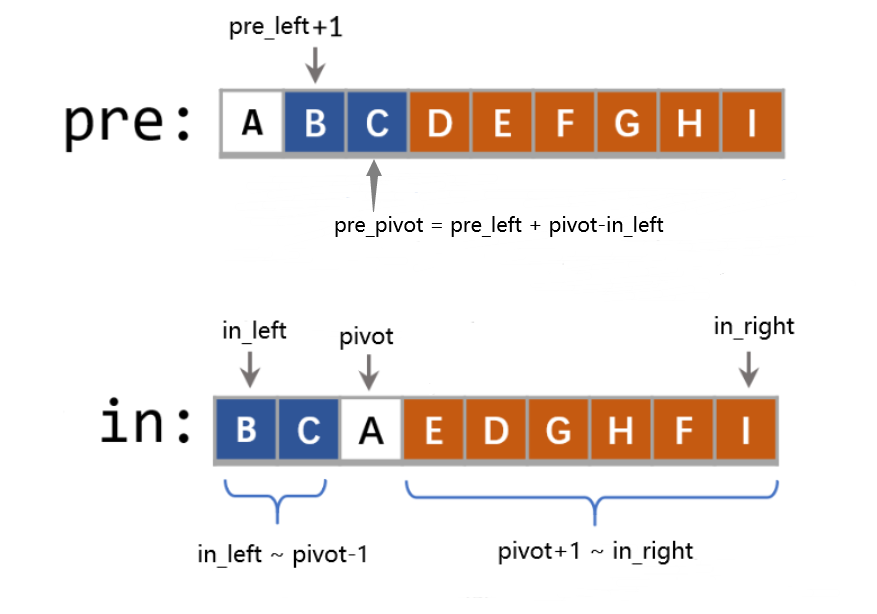
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder){
auto self = [&](auto &&self,
int pre_left, int pre_right, int in_left, int in_right)->TreeNode*{
// 递归出口:只需要前序的左右指针符合即可
if (pre_left > pre_right) return nullptr;
// 1. 将前序序列的第一个结点作为根节点
TreeNode *root = new TreeNode(preorder[pre_left]);
// 2. 找到前序序列的第一个结点在后序序列中的位置作为划分
int pivot = in_left;
for (; pivot <= in_right; ++pivot){ // key:注意初始化
if (inorder[pivot] == preorder[pre_left]) // key:查找中序的pivot
break;
}
// 3. 计算前序数组中的划分位置
int pre_pivot = pre_left + pivot - in_left;
// 4. 建立二叉树
root->left = self(self, pre_left+1, pre_pivot, in_left, pivot-1);
root->right = self(self, pre_pivot+1, pre_right, pivot+1, in_right);
return root;
};
return self(self, 0, preorder.size()-1, 0, inorder.size()-1);
}
106. 从中序与后序遍历序列构造二叉树
-
106. 从中序与后序遍历序列构造二叉树
- 通过始末位置指示容器范围,避免每次调用的vector创建开销
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
auto self = [&](auto &&self,
int in_left, int in_right, int post_left, int post_right)->TreeNode*{
// 递归出口
if (post_left > post_right) return nullptr;
// 建立根结点
TreeNode *root = new TreeNode(postorder[post_right]);
// 在中序数组中查找划分位置
int pivot = in_left;
for (; pivot <= in_right; ++pivot) {
if (inorder[pivot] == postorder[post_right])
break;
}
// 建立左右子树
int post_pivot = post_right - (in_right - pivot);// key:注意括号
root->left = self(self, in_left, pivot-1, post_left, post_pivot-1);
root->right = self(self, pivot+1, in_right, post_pivot, post_right-1);
return root;
};
return self(self, 0, inorder.size()-1, 0, postorder.size()-1);
}
二叉搜索树(考察较少,留后处理)
基础知识
相关题目
98. 验证二叉搜索树
- 98. 验证二叉搜索树
- 中序遍历下,输出的二叉搜索树节点的数值是有序序列
// **********中序遍历,形成一个递增数组************** vector<int> vec; void inorder(TreeNode *root){ if(root == nullptr) return ; inorder(root->left); vec.push_back(root->val); inorder(root->right); } // 判断是否中序遍历的数组是递增的 bool isValidBST(TreeNode* root){ inorder(root); for(int i = 0; i < vec.size()-1; ++i){ if(vec[i] >= vec[i+1])// 二叉搜索树的中序排列是严格递增的 return false; } return true; } // *********************纯递归********************** bool isValid(TreeNode* current,long left,long right){ // 单层逻辑 if(current==nullptr) return true; else if(current->val<=left||current->val>=right) return false; // 递归 return isValid(current->left,left,current->val) &&isValid(current->right,current->val,right); } bool isValidBST(TreeNode* root) { return isValid(root,LONG_MIN,LONG_MAX); }
530. 二叉搜索树的最小绝对差
- 530. 二叉搜索树的最小绝对差
- 思路:中序遍历下,输出的二叉搜索树节点的数值是有序序列。顺序判断相邻值的绝对值,保存最小的即可
- 双指针在树内应用,双指针本质是对于一个序列的遍历。
int getMinimumDifference(TreeNode* root) { // 初始化条件 stack<TreeNode*> st; if(root != nullptr) st.push(root); int res = INT_MAX; TreeNode *prior = new TreeNode(-1000000); while(!st.empty()){ TreeNode* cur = st.top(); if(cur != nullptr){ st.pop(); // 中序遍历 if(cur->right) st.push(cur->right); st.push(cur); st.push(nullptr); if(cur->left) st.push(cur->left); }else{ st.pop(); cur = st.top(); st.pop(); // 节点处理 res = min(res, cur->val - prior->val); prior = cur;// 迭代条件 } } return res; }
236. 二叉树的最近公共祖先
- 236. 二叉树的最近公共祖先
- 后序遍历是一个天然的
自低向上的回溯过程 - 状态的向上传递:通过判断左右子树是否出现了p和q,如果出现p或q则通过回溯值上传到父节点
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if(root == NULL) return NULL; // 每次对返回的结点进行 if(root == p || root == q) return root; TreeNode* left = lowestCommonAncestor(root->left, p, q); TreeNode* right = lowestCommonAncestor(root->right, p, q); // 结点的处理是:尽量返回结点 if(left == NULL) return right; if(right == NULL) return left; if(left && right) // p和q在两侧 return root; return NULL; // 必须有返回值 } - 后序遍历是一个天然的
235. 二叉搜索树的最近公共祖先
- 235. 二叉搜索树的最近公共祖先
- 思路:自上而下搜索,遇到的第一个节点值在p和q之间的值即为最近公共祖先
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { while(root) { if (root->val > p->val && root->val > q->val) { root = root->left; } else if (root->val < p->val && root->val < q->val) { root = root->right; } else return root; } return NULL; }
450. 删除二叉搜索树中的节点
- 450. 删除二叉搜索树中的节点
- 思路:框架
TreeNode* deleteNode(TreeNode* root, int key) { // 健壮性检查 if(root == nullptr) return nullptr; // 基本初始化 TreeNode *cur = root; TreeNode *prior = root; while (cur != nullptr){ // 符合条件值的处理 if(cur->val == key){ if(cur->left == nullptr || cur->right == nullptr){ // 两个都空 if(cur->left == nullptr && cur->right == nullptr) return nullptr; // 被删除节点只有一个孩子或均为空 if(key < prior->val){// cur是左子树 prior->left = cur->right; return root; }else{ prior->right n = cur->right; return root; } }else{ // 被删除节点有两个孩子 TreeNode *curLeft = cur->left; cur = cur->right; while(cur->left != nullptr){ cur = cur->left; } cur->left = curLeft; if(key < prior->val){// cur是左子树 prior->left = prior->left->right; return root; }else{ prior->right = prior->right->right; return root; } } } prior = cur;// 前迭代 // 左右节点处理 if(key < cur->val){ if(cur->left){ cur = cur->left; }else{// 找不到 return root; } }else{ if(cur->right){ cur = cur->right; }else{// 找不到 return root; } } } return root; }
669. 修剪二叉搜索树
- 669. 修剪二叉搜索树
// 1. 确定递归函数的返回类型及参数,返回类型是递归算法的输出值类型,参数是递归算法的输入 TreeNode* trimBST(TreeNode* root, int low, int high) { // 2. 递归终止条件 if (root == nullptr ) return nullptr; // 3.节点处理:return保留的状态 if (root->val < low) {// 保留更大的右半部分 TreeNode* right = trimBST(root->right, low, high); return right; } if (root->val > high) {// 保留更小的左半部分 TreeNode* left = trimBST(root->left, low, high); return left; } // 4.迭代条件 root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子 root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子 return root; }
108. 将有序数组转换为二叉搜索树
- 108. 将有序数组转换为二叉搜索树
TreeNode* traversal(vector<int>& nums, int left, int right) { // 递归出口 if (left > right) return nullptr; // 运算 int mid = left + ((right - left) / 2);// 防止求和溢出 TreeNode* root = new TreeNode(nums[mid]); // 递归迭代 root->left = traversal(nums, left, mid - 1); root->right = traversal(nums, mid + 1, right); return root; } // 主调函数 TreeNode* sortedArrayToBST(vector<int>& nums) { TreeNode* root = traversal(nums, 0, nums.size() - 1); return root; }
669. 修剪二叉搜索树
- 669. 修剪二叉搜索树
// 1. 确定递归函数的返回类型及参数,返回类型是递归算法的输出值类型,参数是递归算法的输入 TreeNode* trimBST(TreeNode* root, int low, int high) { // 2. 递归终止条件 if (root == nullptr ) return nullptr; // 3.节点处理:return保留的状态 if (root->val < low) {// 保留更大的右半部分 TreeNode* right = trimBST(root->right, low, high); return right; } if (root->val > high) {// 保留更小的左半部分 TreeNode* left = trimBST(root->left, low, high); return left; } // 4.迭代条件 root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子 root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子 return root; }
🚩点此跳转到首行↩︎
参考博客
- 「代码随想录」47. 全排列 II:【彻底理解排列中的去重问题】详解
- codetop