文章目录
- 基础概念
- 曲线拟合的流程
- 极小化损失函数
- 线性最小二乘
- 超定方程组的最小二乘解(必考)
- 例题(必考)
- 使用法方程计算拟合方程
- 使用最小二乘法求解
- 总结
基础概念
曲线拟合的流程
- 选取函数类
- 选取参数的准则:极小化损失函数
- 求解优化问题,得到拟合参数
极小化损失函数
- 函数空间声明

- 残差定义
- 残差:观测值和估计值的差


- 问题转化:将最小化损失函数转变为求极小值,求解函数零点的问题

-
求偏导推导过程
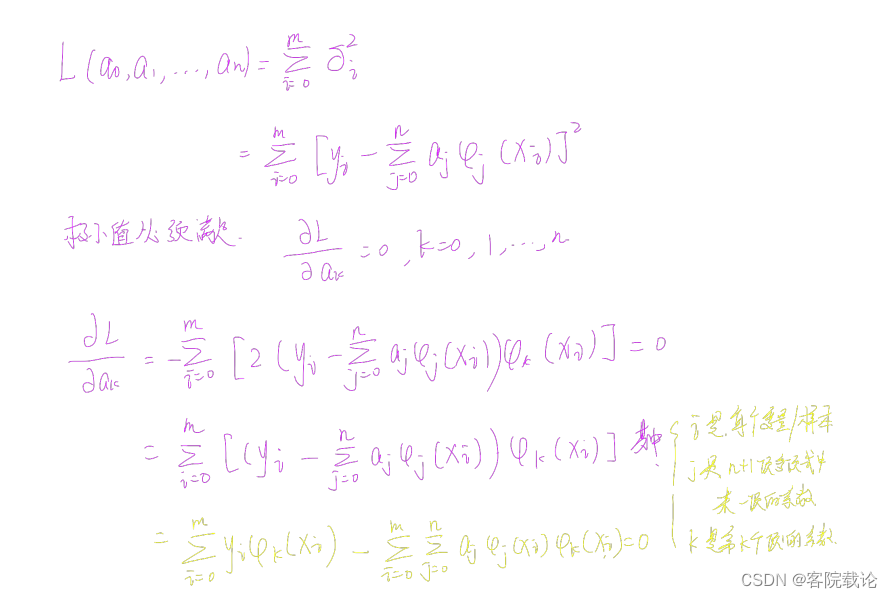
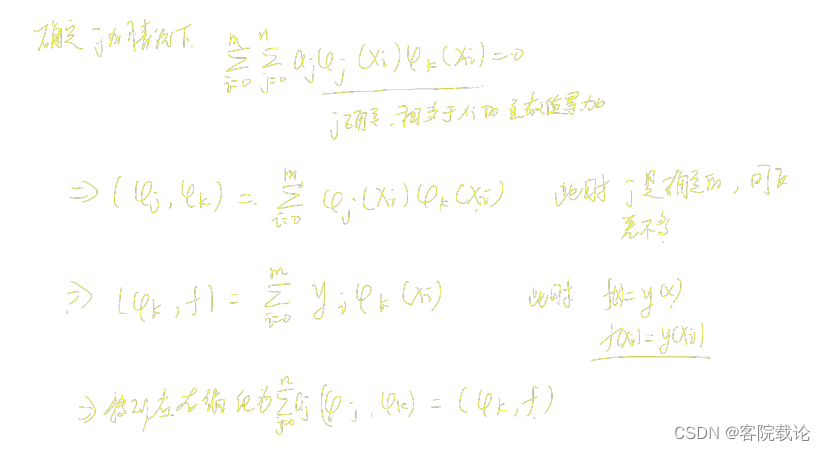
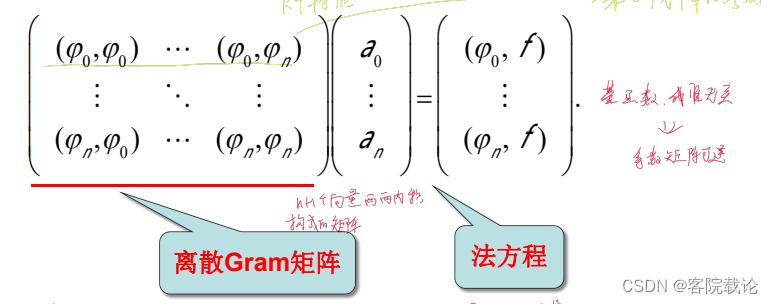
-
具体样例(法方程,这里必须要会)
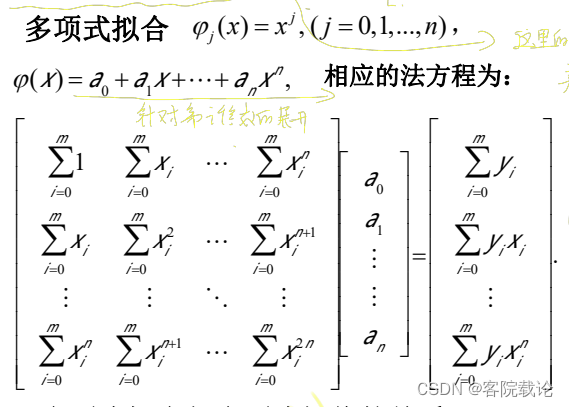
-
例题,一次函数写出法方程


线性最小二乘
- 线性最小二乘的推导

超定方程组的最小二乘解(必考)
-
超定方程:方程的个数大于未知数的个数


-
将超定方程组转变为法方程进行求解,使用上述的矩阵乘法进行转换
例题(必考)
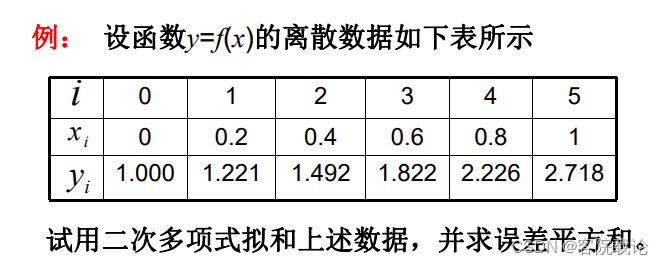
使用法方程计算拟合方程
- 根据之前的推导直接写出法方程,然后求解


使用最小二乘法求解

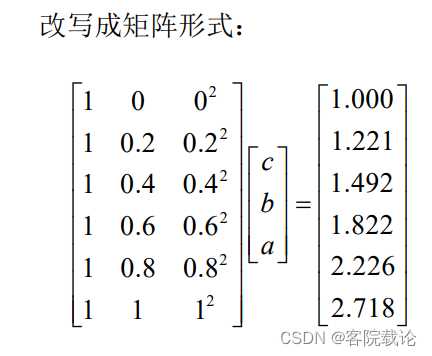


总结
- 线性最小二乘法,是必考的,会用法方程进行求解,同时也会使用线性最小而二乘求解