前言
本文将用最干最简单的方式告诉你怎么将Stable Diffusion AI图像生成软件部署到你的本地环境
关于Stable Diffusion的实现原理和训练微调请看我其他文章
部署Stable Diffusion主要分为三个部分
- 下载模型（模型可以认为是被训练好的，生成图像的大脑）
- 部署Web UI（可通过浏览器访问的操作界面，可以更方便的生成图像、设置参数）
- 部署环境（Python、Pytorch等运行环境和Stable Diffusion本体）
一 下载模型
模型链接
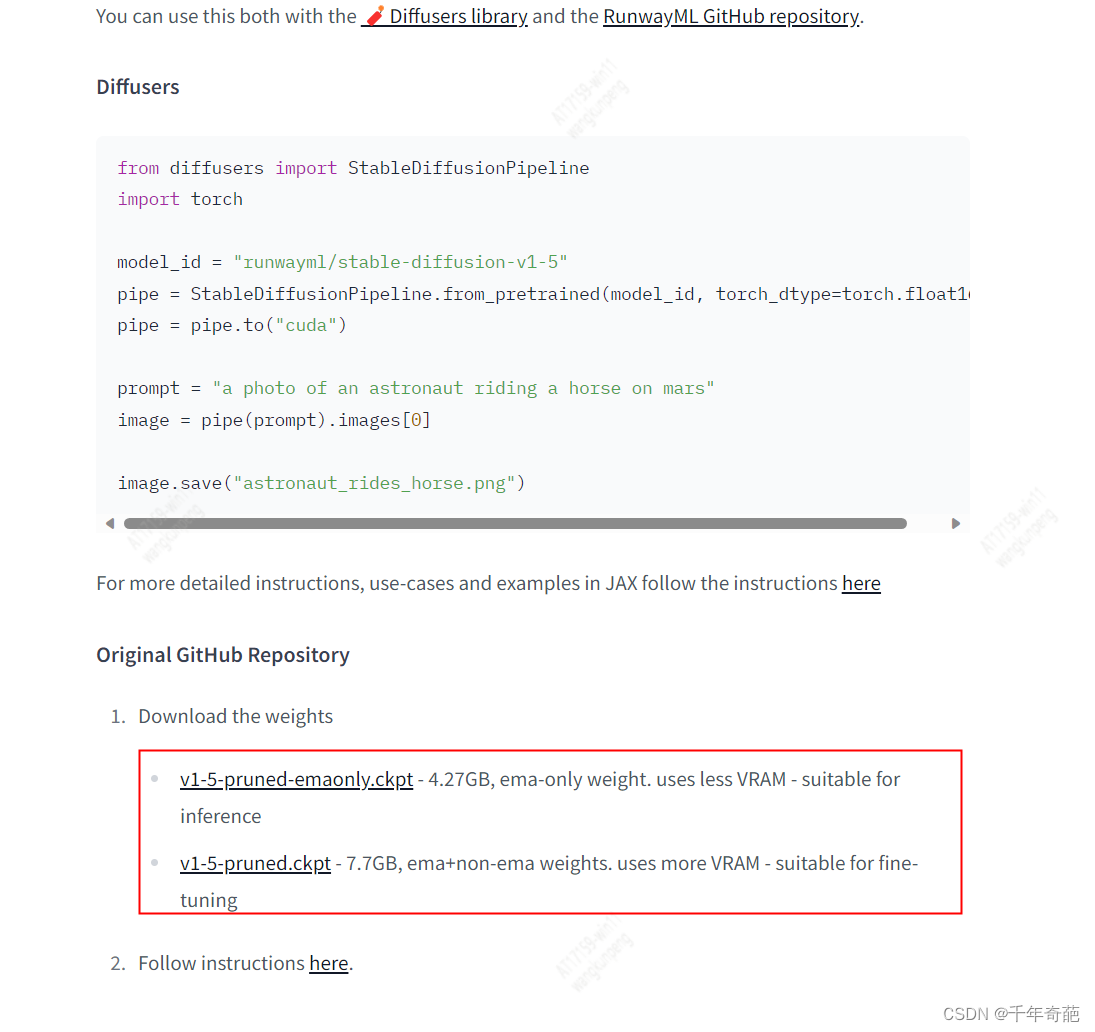
进入页面后下方有两个可下载的模型，4.27GB对应小显存显卡(小于6GB)，7.7GB版本对应高显存显卡
Stable Diffusion项目中自带4.27GB版本的模型，所以如果你的显卡够硬，可以手动下载7.7GB版本
二 部署Web UI
这玩意是个可视化网页操作台，在这里可以选择模型、调整参数，执行训练、生成等任务，可以说代码以外的大部分操作都得靠它
首先确保你本地已经安装了Git
然后使用git 克隆项目，在控制台中输入：git clone https://github.com/AUTOMATIC1111/stable-diffusion-webui.git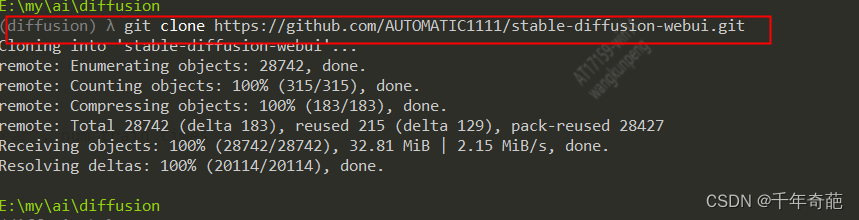
三 部署环境
Web UI下载完成后进入刚下载的目录，开始安装Diffusion依赖包
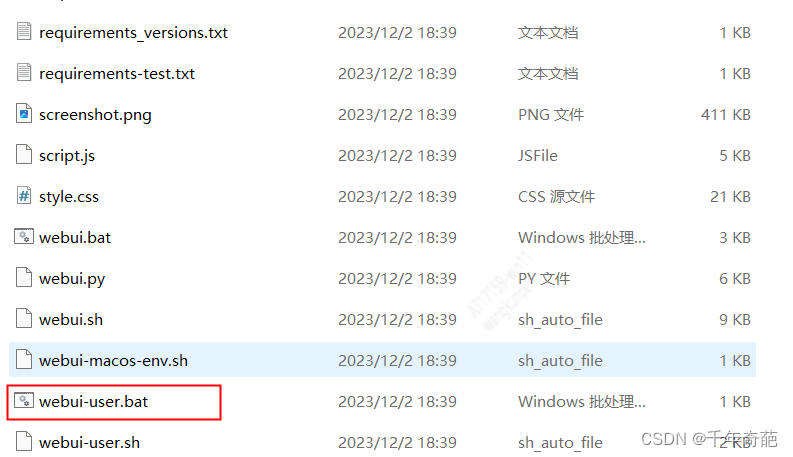
如果是windows平台就运行webui-user.bat，如果是mac os就运行webui-macos-env.sh
安装过程很长，建议打两局拳皇
如果你想用conda环境，那么请在控制台中切换好环境，然后再执行安装脚本
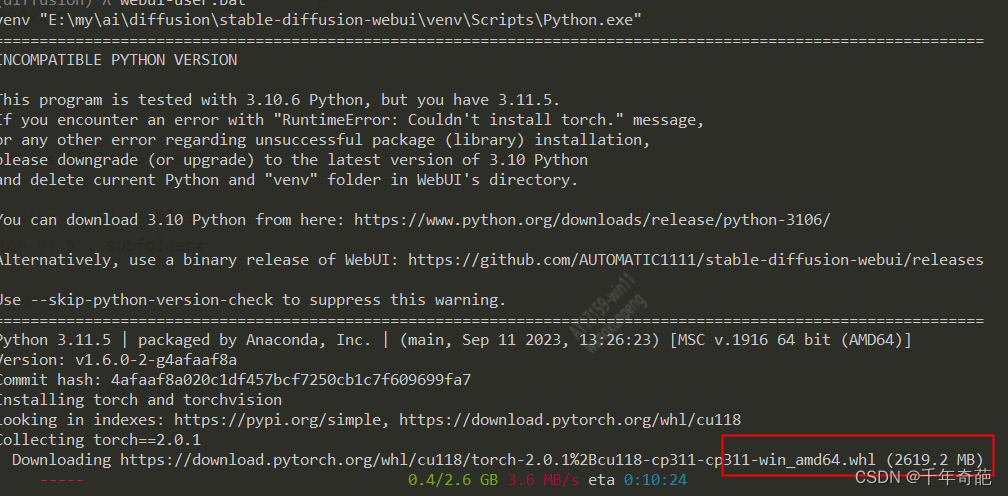
安装完成后会自动打开网页
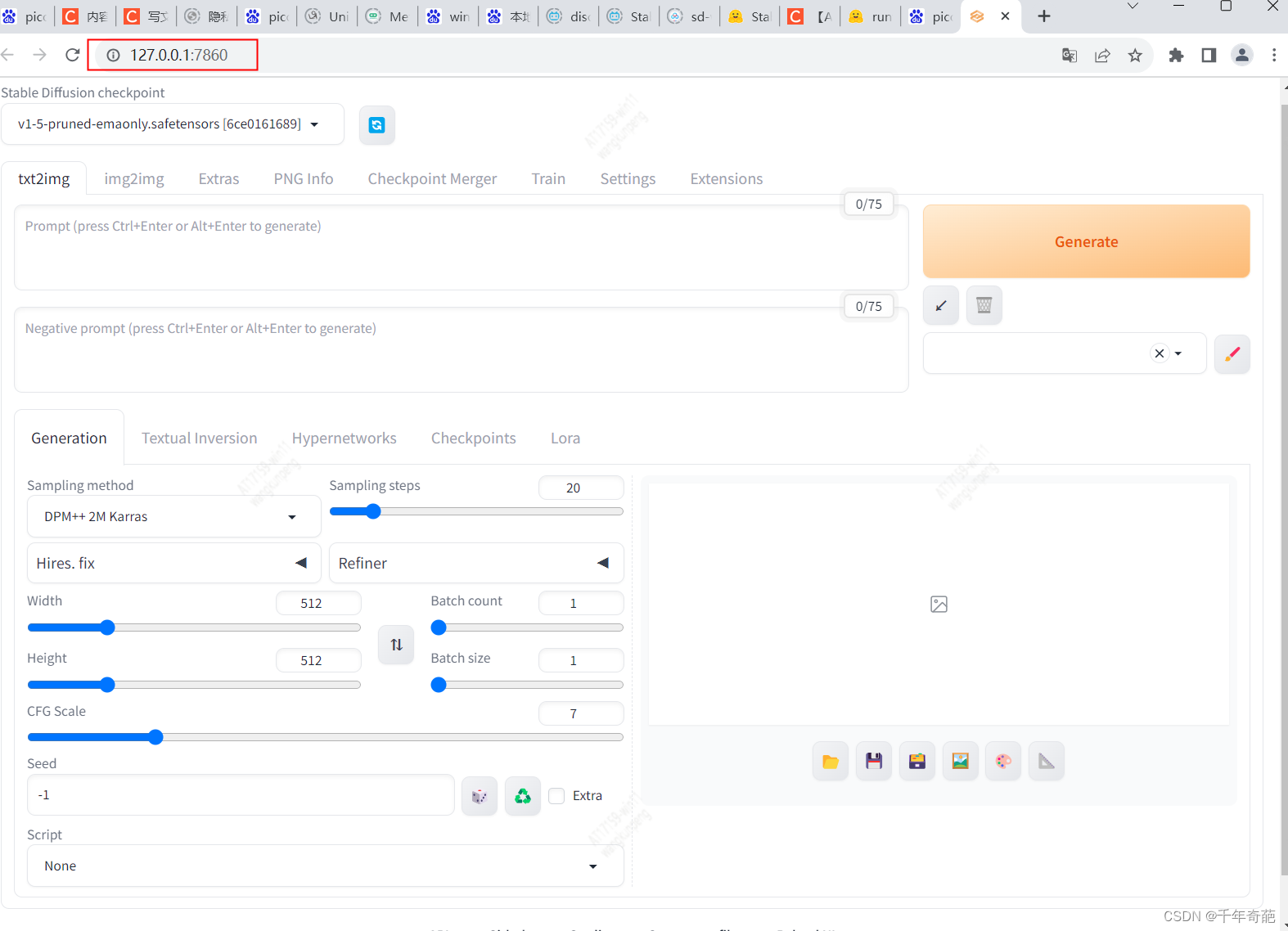
四 测试图像生成
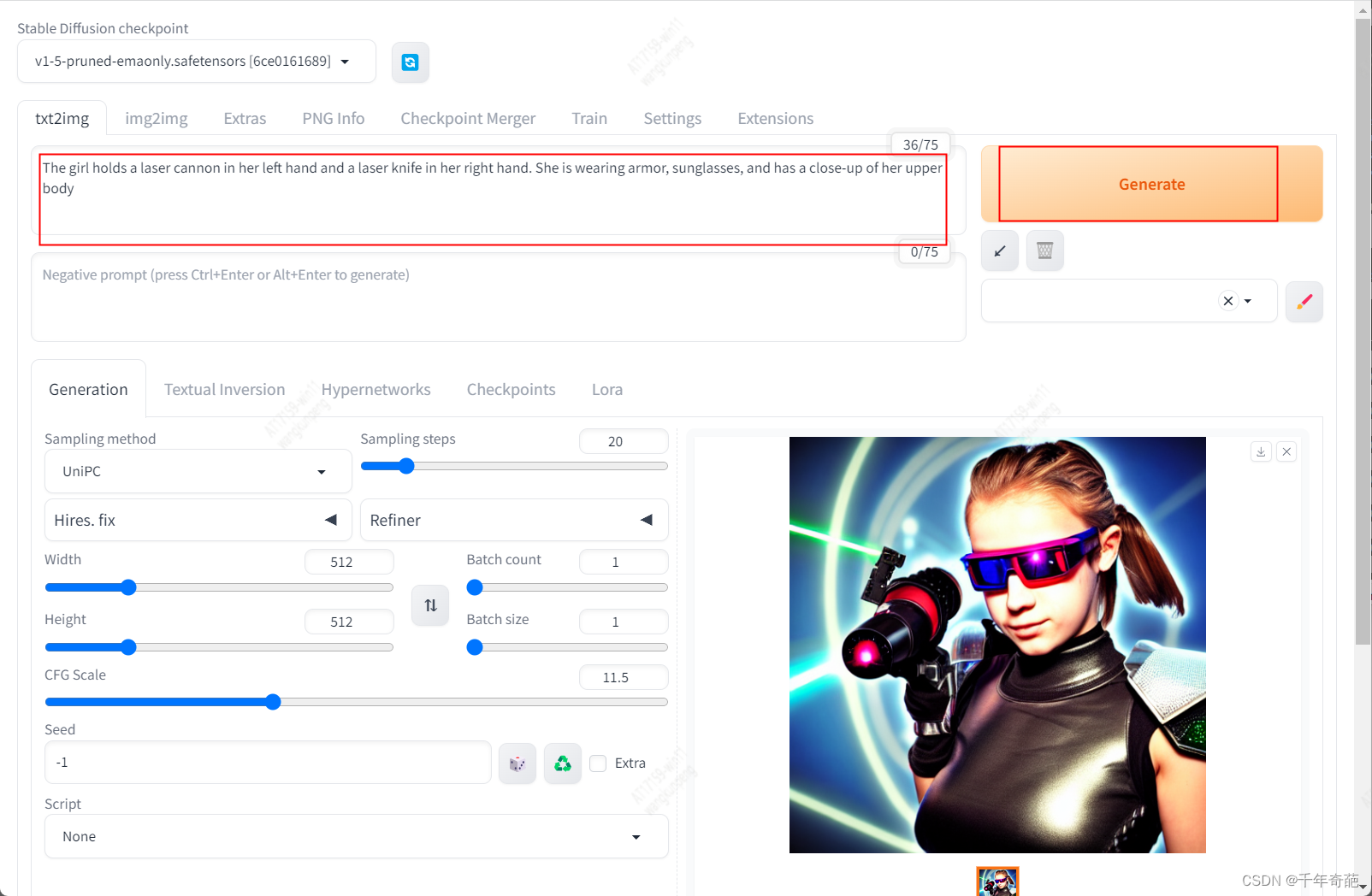
在网页中，txt2img一栏填入关键字，
例如： the girl holds a laser cnannon in her left hand and a laser knife in her right hand
然后点击右侧的Generate按钮，即可在下方看到生成结果
五 界面汉化
是中国人就说中国话
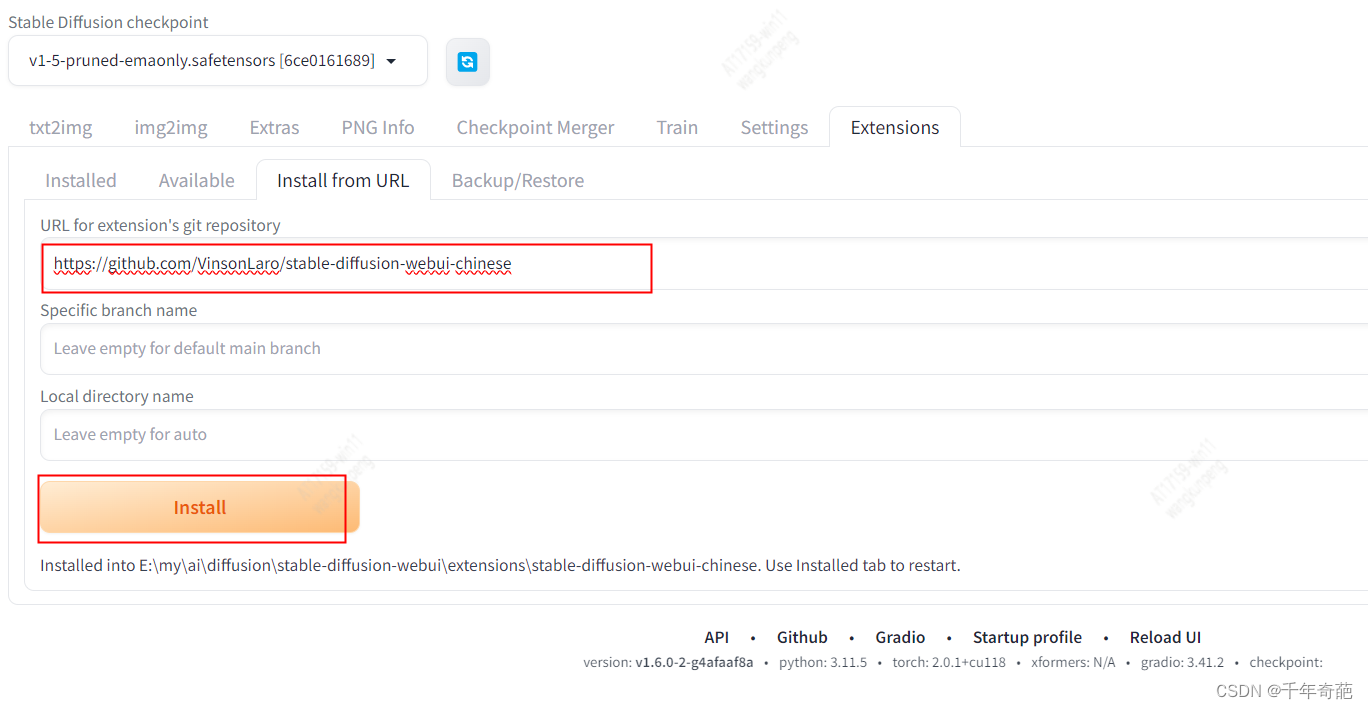
还是进入刚才的web ui界面，找到Extensions栏->Install from URL->URL for extension’s git repository
填入项目地址：https://github.com/VinsonLaro/stable-diffusion-webui-chinese
然后点击下方的Install按钮
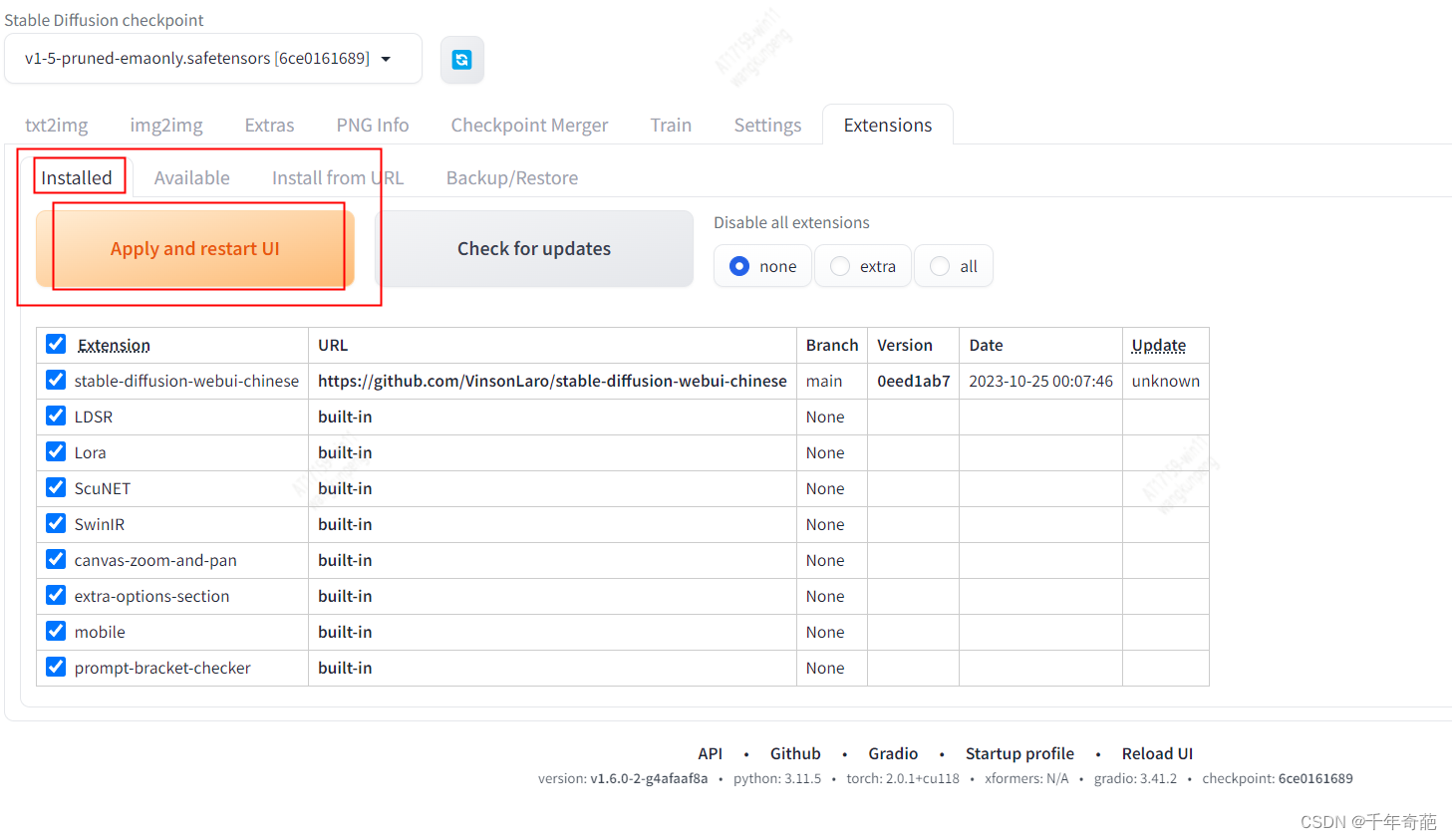
安装完成后进入Installed栏，点击Apply and restart UI进行重启
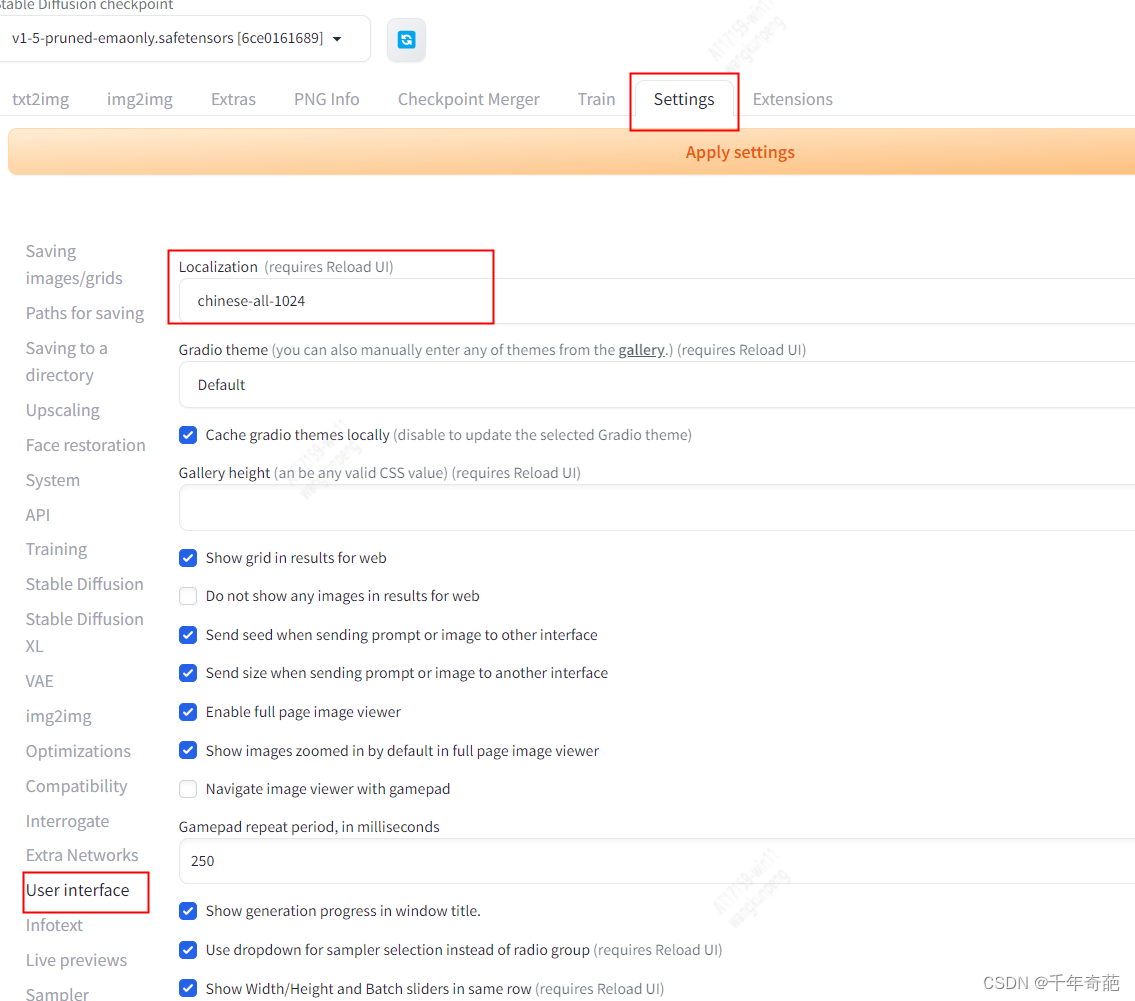
点击"Settings"，左侧点击"User interface"界面，在界面里最下方的"Localization (requires restart)“，选择"Chinese-All"或者"Chinese-English”
点击界面最上方的黄色按钮"Apply settings"，再点击右侧的"Reload UI"即可完成汉化
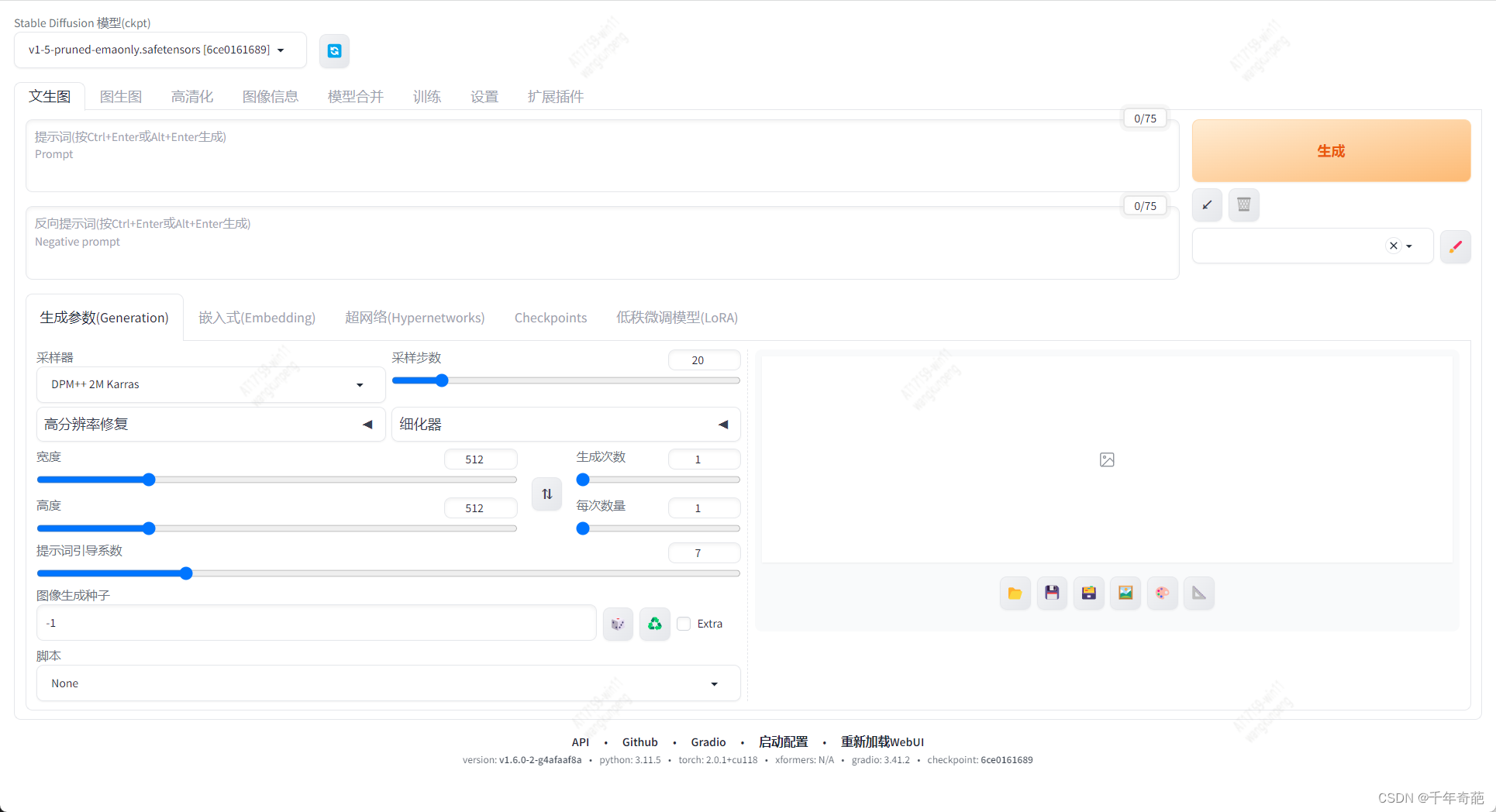
完成汉化后长这样
六 选择模型
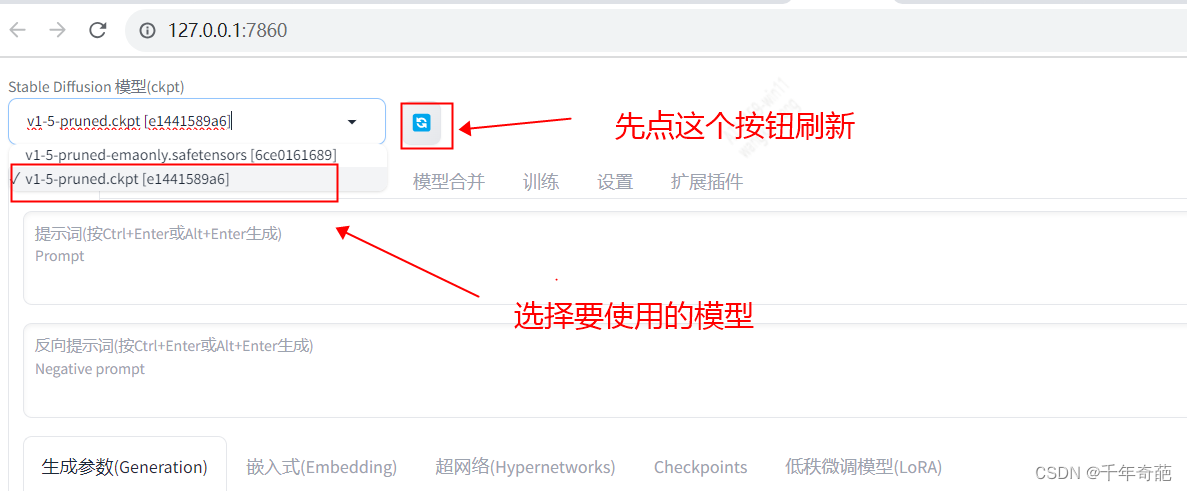
模型的目录位置在项目中的models目录下。进入该目录会看到里面有很多子目录，模型文件一般放在Stable-diffusion目录下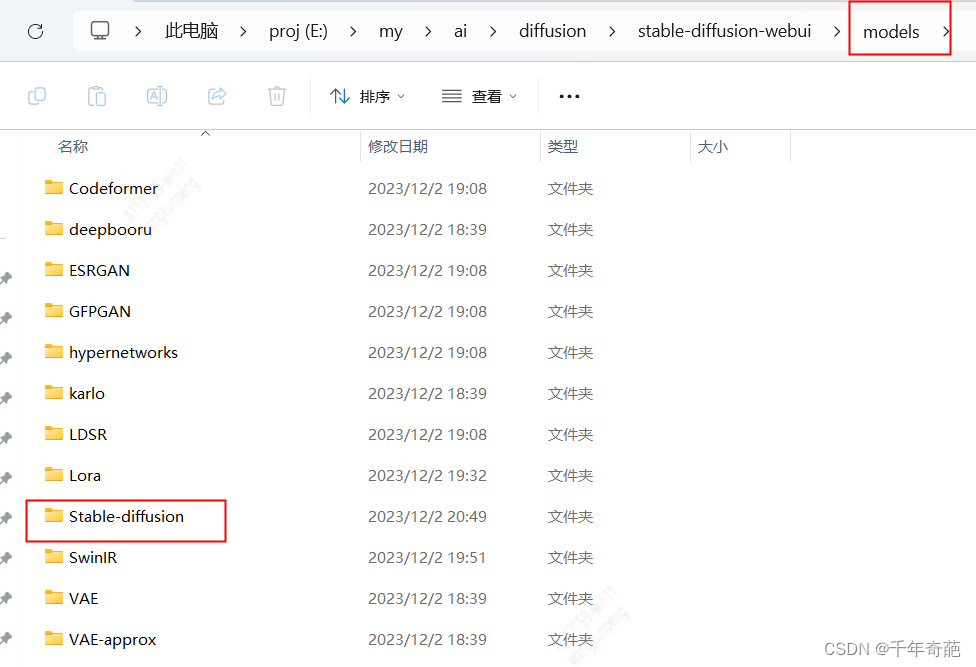
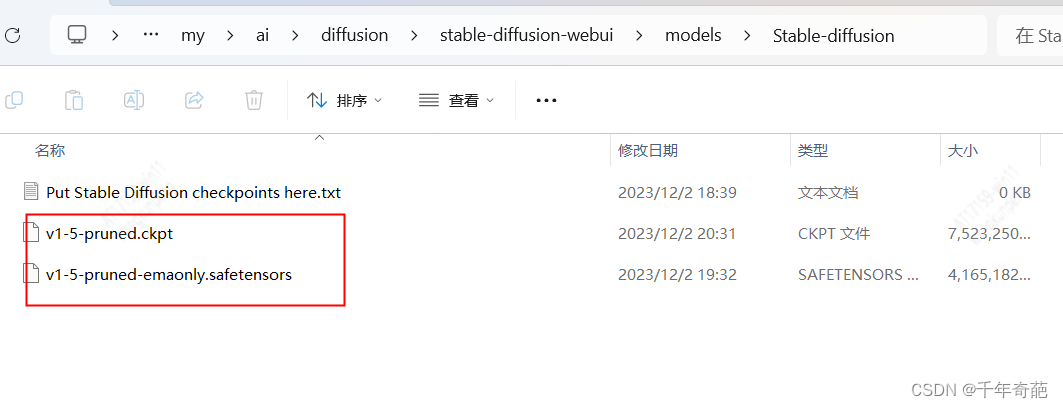
然后回到ui 首页，点击刷新按钮刷新出模型，选择后等待解析完成即可使用
七 其他资源（均免费）
Stable Diffusion 官方模型：
https://huggingface.co
另一个比较火的模型 网站
https://civitai.com/
附
关于Stable Diffusion预训练、微调训练在我的另一个贴子中，有兴趣可以看看
