原文链接

Hui Liu, Wenya Wang, and Haoliang Li. 2023. Interpretable Multimodal Misinformation Detection with Logic Reasoning. In Findings of the Association for Computational Linguistics: ACL 2023, pages 9781–9796, Toronto, Canada. Association for Computational Linguistics.

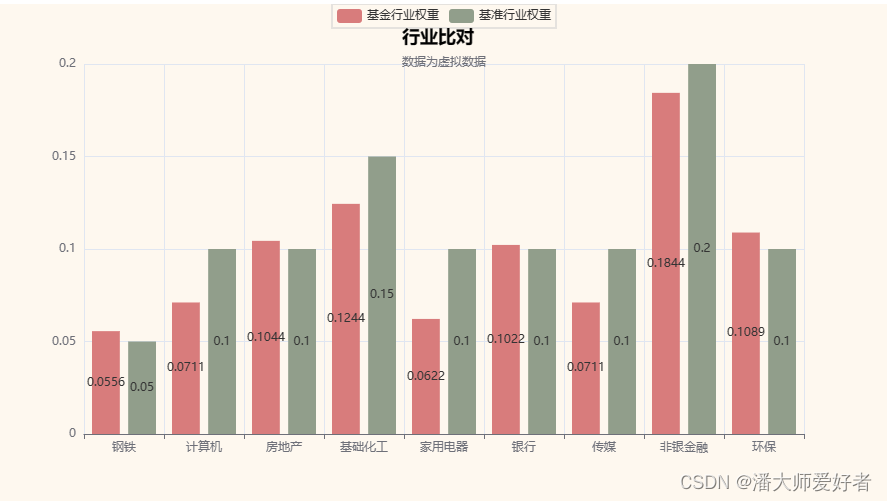
核心：多模态、可解释

基本架构

输入为文本$T$和图片$I$，（此处貌似只允许输入一张图片，而实际上情况中可能不止一张）

使用Tokenizer处理$T$，另用CNN处理$I$，将处理后的feature用GCN组合到一起得到object $o$，由

Methodology

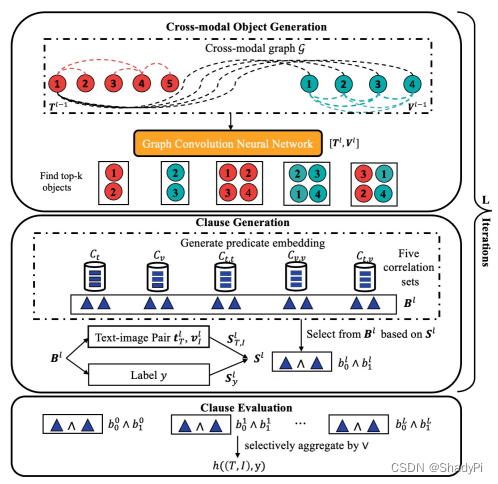
Feature Extraction

对于文本$T$，先将其分割成$m$个token，对每个token再使用BERT+一层LSTM将其转换为$d$维的向量${\text{X}}_T$，$m$个token总共得到$\text{T}\in {\mathcal{R}}^{m\times d}$

对于图片$I$，先resize到$224\times 224$，再划分为$z=r^2$个patch，每个patch大小为$224/z\times 224/z$，每个patch使用ResNet34+ViT+2层MLP转化为$d$为向量${\text{X}}_I$，最后得到$\text{I}\in {\mathcal{R}}^{r\times d}$

Cross-modal Object Generation

在这一步，生成单模态和跨模态的隐式表征。

在这篇工作中，定义了5种Object，分别是单文本、单图像、双文本、双图像以及文本图像混合，如下所示。

在上一步得到若干feature后，我们通过GCN将这些feature结合起来，将之前提取出的${\text{X}}_T,{\text{X}}_I$当作GCN中的节点，这些节点的embedding就是一个$d$维向量。在连GCN的边时，使用Spacy技术寻找token之间的依赖关系，在存在依赖关系的token之间连边，而对每个patch则是将在原图片里相邻的patch连在一起，而文本和图片之间则是直接全连接的。

GCN的初始输入${\text{H}}^0=[\text{T},\text{I}]\in {\mathcal{R}}^{(m+r)\times d}$，邻接矩阵$\text{A}\in {\mathcal{R}}^{(m+r)\times (m+r)}$ ，每一层graph都有一个线性变换权重矩阵$W\in {\mathcal{R}}^{d\times d}$，整个GCN的转移方程为${\text{H}}^l=\text{ReLU}({\text{D}}^{-\frac{1}{2}}\text{A}{\text{D}}^{-\frac{1}{2}}{\text{H}}^{l-1}{\text{W}}^l)$。如此即可得到每一层的每个节点的feature，即 H l = [ T l , V l ] , l ∈ { 0 , 1 , 2 , ⋯   , L } \textbf{H}^l=[\textbf{T}^l, \textbf{V}^l], l\in \{0, 1, 2, \cdots, L\} Hl=[Tl,Vl],l∈{0,1,2,⋯,L}。

利用这些feature，即可根据上表中的公式计算出每层的5种Objects，分别是${\text{O}}_t^l\in {\mathcal{R}}^{m\times d},{\text{O}}_v^l\in {\mathcal{R}}^{r\times d},{\text{O}}_{t,t}^l\in {\mathcal{R}}^{(m\times m)\times d},{\text{O}}_{v,v}^l\in {\mathcal{R}}^{(r\times r)\times d},{\text{O}}_{t,v}^l\in {\mathcal{R}}^{(m\times r)\times d}$

每种$\text{O}$中的小$\text{o}\in {\mathcal{R}}^d$会再通过一个一层+ReLU的MLP，得到一个分数。每个种类的$\text{O}$种top-k的object会被抽出，记作${\hat{\text{O}}}_t^l,{\hat{\text{O}}}_v^l,{\hat{\text{O}}}_{t,t}^l,{\hat{\text{O}}}_{v,v}^l,{\hat{\text{O}}}_{t,v}^l$，均属于${\mathcal{R}}^{k\times d}$。为了让这个过程可以反向传播，实现的时候可以通过disable其他非top-k的节点实现。

Clause Generation

得到这些object的feature之后，我们就要计算他们支持不同label的概率，首先要得到对应body predicate，比如$b_t(t,y)$ 的表征，记作${\text{B}}_t\in {\mathcal{R}}^{k\times d}$，其他同理。${\text{B}}_t$计算如下
$${\text{B}}_t=\text{sparsemax}([{\hat{\text{O}}}_t,\text{y}]{\text{W}}_t^e{\text{C}}_t^T){\text{C}}^T$$$[{\hat{\text{O}}}_t,\text{y}]\in {\mathcal{R}}^{k\times 2d},其中\text{y}\in {\mathcal{R}}^{k\times d}$为label的$d$维表征广播为$k\times d$的产物，${\text{W}}_t^e\in {\mathcal{R}}^{2d\times d}$为可学习参数，${\text{C}}_t\in {\mathcal{R}}^{g\times d}$则是预先定义的correlation（这里的“预先定义”指每个correlation对应的predicate是先定义好的，实际上也是随机初始化的）但在训练过程中也是可学习的。

以此类推，我们也可以得到其他几种predicate的表征，$\text{B}=[{\text{B}}_t,{\text{B}}_v,{\text{B}}_{t,t},{\text{B}}_{v,v},{\text{B}}_{t,v}]\in {\mathcal{R}}^{5k\times d}$（这应该只是一个label对应的表征，严格来说应该写作${\text{B}}_y$作为区分）。

除了这几个从GCN里提取的表征，我们还对整个文本和图片进行了编码，文本的编码${\text{t}}_T={\text{T}}^T\text{softmax}(\text{T}{\text{W}}_T)\in {\mathcal{R}}^d$，图片的编码${\text{v}}_I={\text{V}}^T\text{softmax}(\text{V}{\text{W}}_I)\in {\mathcal{R}}^d$，其中${\text{W}}_T,{\text{W}}_I$均属于${\mathcal{R}}^{d\times 1}$为可学习参数，注意与之前一层的打分MLP不是参数共用的。

接下来，我们计算两种attention score，分别是
$$\begin{gathered} {\text{S}}_{T,I}=\text{sparsemax}(\text{B}{\text{X}}_{T,I}[{\text{t}}_T,{\text{v}}_I]), \\ {\text{S}}_y=\text{sparsemax}([\text{B},\text{y},\text{B}-\text{y},\text{B}\circ \text{y}]{\text{W}}_y) \end{gathered}$$其中，${\text{X}}_{T,I}\in {\mathcal{R}}^{d\times 2d},{\text{W}}_y\in {\mathcal{R}}^{4d\times 1}$均为可学习参数。这两个分数一个注重news的内容（文本和图片），另一个注重和label的关系，最终两个score再合为一个score，$\text{S}\in {\mathcal{R}}^{5k}$
$$\text{S}=\text{sparsemax}({\text{S}}_{T,I}\circ {\text{S}}_y)$$每个分数描述了其对应的clause（根据我的理解，predicate是模板，填入内容后称为clause）与判断整个news是否为真的相关性，因此我们并不需要将整个$5k$个clause全部用到，而是筛选其中一部分，即top-$\lfloor 5k\times \beta \rfloor$的predicate。这些筛选出的clause进入下一个step。

Clause Evaluation

以上只是生成clause的过程，最终目的还是要判断这个news是不是真的。从可解释性的角度出发，一个news为不为真的可以从某些clause为不为真推导出来，因此我们需要先得到这些clause为真的概率。

对于$b_t(t,y)$，他的truth value可以计算为：
$$\mu (b_t(t,y))=\text{sigmoid}([{\text{b}}_t,\text{p},{\text{b}}_t-\text{p},{\text{b}}_t\circ \text{p}]{\text{W}}_{\mu })$$其中，$\text{p}={\text{o}}_t\circ \text{y}\in {\mathcal{R}}^d,{\text{W}}_{\mu }\in {\mathcal{R}}^{4d\times 1}$为可训练参数，${\text{b}}_t\in {\mathcal{R}}^d$是从${\text{B}}_t$的对应行中取出的。

将这些clause的truth value用and运算连接，即可得到对应label的概率。更进一步，由于GCN中每层都会输出一组${\hat{\text{O}}}_t^l,{\hat{\text{O}}}_v^l,{\hat{\text{O}}}_{t,t}^l,{\hat{\text{O}}}_{v,v}^l,{\hat{\text{O}}}_{t,v}^l$，因此我们也会得到$L$组object及其后面的clause，这些clause可以看作是相对独立的，因此可以用or运算连接。记第$l$层第$i$个clause的truth value为$b_i^l$，则整则news为label $y$的概率为
$$(b_1^0\wedge \cdots )\vee (b_1^1\wedge \cdots )\vee \cdots \vee (b_1^L\wedge \cdots )\Rightarrow h((T,I),y)$$这里的and和or运算使用product T-norm，即$a\wedge b=ab,a\vee b=1-(1-a)(1-b)a,b\in [0,1]$

对于每个label $y$，都算出一个truth value，使用cross-entropy计算loss。

实验

指标

在三个数据集上实施了实验，两个misinformation数据集Twitter和Weibo，一个sarcasm数据集sarcasm。


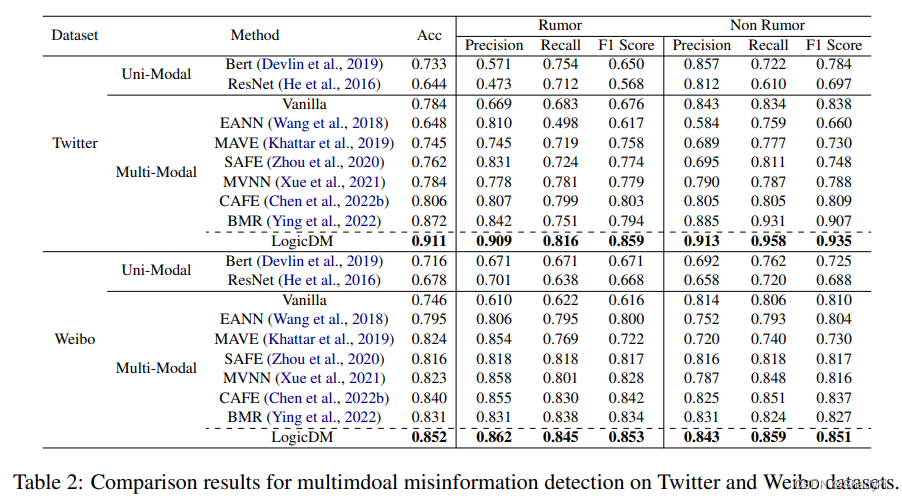
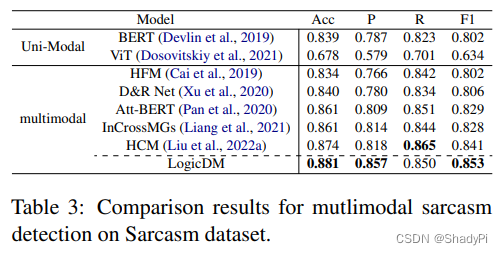
从准确性来讲，很好，都是SOTA，而且在有一定解释性的基础上还提升了模型性能。另外，Precision明显要比其他的模型好，可能是logic帮助模型更好的学习到了rule而不是对噪声过拟合。

可解释性

cd展现出模型会根据文本中是否有足够清晰的表述来判断一则消息是否是rumor，a则是模型发现图片中有地方是P的，b则是人类不是很能理解但判断对了的例子。

消融实验

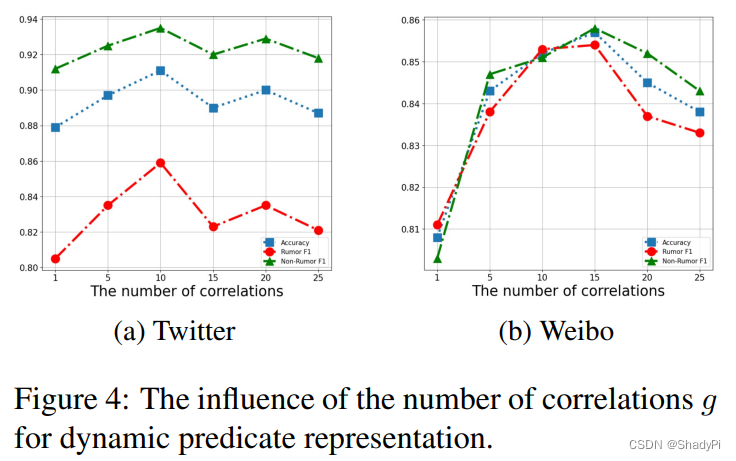
调整Correlation的多少，即$g$，发现最初随着$g$升高，performance一路升高，但到达一个峰值后缓慢下降。

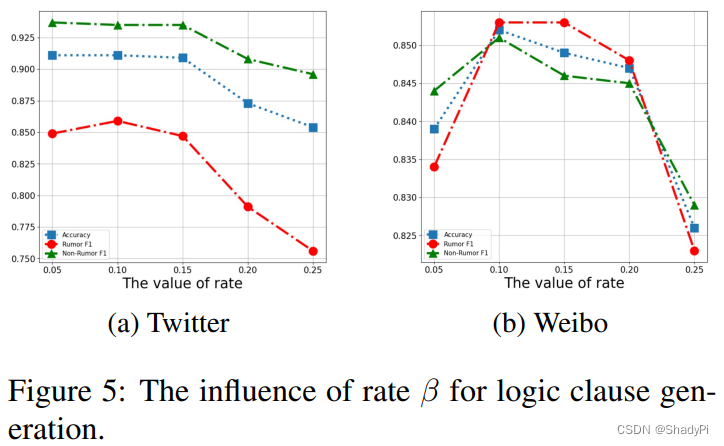
调整筛选Clause的阈值，即$\beta$，发现在$\beta$超过$0.15$后性能急剧下降，可能有两个原因：1）选出来的clause多了以后，conjunction的操作会导致指数消失，最后得到的概率很小。2）选出来的clause太多，包含了一些低分的clause，引入了噪声。

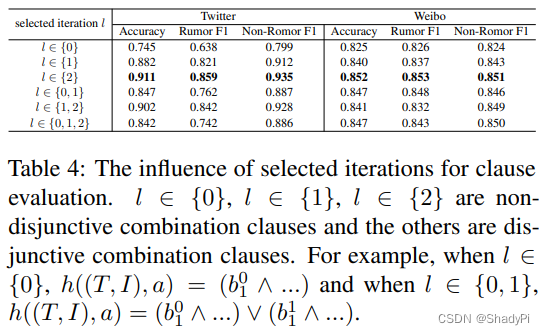
同时，考察GCN不同Layer的选取对实验结果的影响，发现只挑选第二层时效果最佳，说明经过多层GCN整合后的多模态信息对判断misinformation更有用，但加了多层以后似乎效果有所下降。

可改进

只支持一张图片，实际操作中可能不止一张图片。
product T-norm 的 conjunction操作容易遭遇概率消失，或许可以使用其他方法连接这些clause的truth value。
文本和图片直接全部匹配连接，这部分是否可以改进？
predicate只能填入两个变量，不知道$t,t$和$v,v$的predicate是否有那么大的作用，因为GCN同样有融合几个feature的功能。