1-理解递归
斐波那契数列(Fibonacci sequence),又称黄金分割数列 ,以兔子繁殖为例子而引入,故又称“兔子数列”,其数值为:1、1、2、3、5、8、13、21、34……特点是 从第三个数开始,第n个数的数值是 前面两个数相加得来。形成公式f(n)=f(n-1)+f(n-2)。这就是递归。
递归算法(recursion algorithm)在计算机科学中是指一种通过重复将问题分解为同类的子问题而解决问题的方法。
满足递归的三个条件:
1.一个问题的解可以分解为几个子问题的解;
2.这个问题与分解之后的子问题,除了数据规模不同,求解思路完全一样;
3.存在递归终止条件。
2-编写递归代码
写递归代码最关键的是写出递推公式,找到终止条件。就是找到如何将大问题分解为小问题的规律,并且基于此写出递推公式,然后再推敲终止条件,最后将递推公式和终止条件翻译成代码。
斐波那契数列的定义是 f(n)=f(n-1)+f(n-2),生成第 n项的做法:把 f(n)问题的计算拆分成 f(n−1)和 f(n−2) 两个子问题的计算,并递归,以 f(0) 和 f(1)为终止条件。
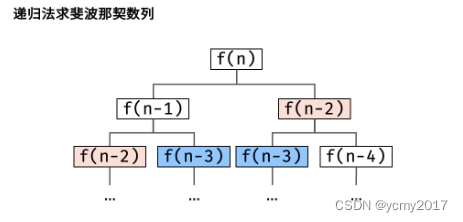
3-警惕递归问题和缺点
警惕无限循环导致栈溢出:在编写的时候要找好递归的终止条件,防止无限循环调用导致的栈溢出;在实际业务中,我们可以约定递归的最大深度,这样也可以防止无限循环调用问题。
警惕重复计算问题:如果按照章节2的思路编写,会有大量的重复计算问题,我们可以考虑思路将已经计算的缓存起来(后续还有其他的算法解决方法,后续讲解),下次直接使用就行,这样就避免大量重复计算问题。