【图像处理OpenCV(C++版)】——3.1几何变换之仿射变换

news2024/11/18 22:55:47

前言：

😊😊😊欢迎来到本博客😊😊😊

🌟🌟🌟 本专栏主要结合OpenCV和C++来实现一些基本的图像处理算法并详细解释各参数含义，适用于平时学习、工作快速查询等，随时更新。

😊😊😊 具体食用方式：可以点击本专栏【OpenCV快速查找(更新中)】–>搜索你要查询的算子名称或相关知识点，或者通过这篇博客👉通俗易懂OpenCV(C++版)详细教程——OpenCV函数快速查找(不断更新中)]查阅你想知道的知识，即可食用。

🎁🎁🎁支持：如果觉得博主的文章还不错或者您用得到的话，可以悄悄关注一下博主哈，如果三连收藏支持就更好啦！这就是给予我最大的支持！😙😙😙

文章目录

    • 学习目标
    • 一、基础知识
    • 二、仿射变换
      • 2.1 平移
      • 2.2 放大和缩小
      • 2.3 旋转
      • 2.4 计算仿射矩阵
      • 2.5 插值算法
      • 2.6 代码实现
    • 三、 总结

学习目标

  • 熟悉仿射变换中平移、放大和缩小、旋转等基本操作
  • 熟悉如何计算仿射矩阵
  • 了解常见插值算法

一、基础知识

  首先，对几何变换做个简单了解。打开任意一个图像编辑器，一般可以有对图像进行放大、缩小、旋转等操作，这类操作改变了原图中各区域的空间关系。对于这类操作，通常称为图像的几何变换。

  一般而言，完成一张图像的几何变换需要两个独立的算法：首先，需要一个算法实现空间坐标变换，用它描述每个像素如何从初始位置移动到终止位置；其次，还需要一个插值算法完成输出图像的每个像素的灰度值。

  本章节就围绕这两个独立的算法进行介绍，从而实现图像的几何变换。几何变换主要包括三种：仿射变换、投影变换和极坐标变换。

  

二、仿射变换

  二维空间坐标的仿射变换可以这样表示：

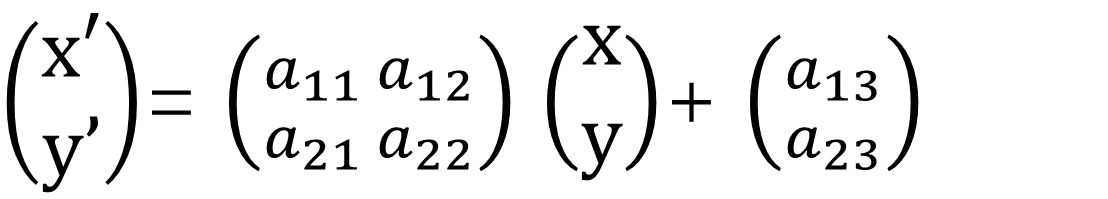
  为了更简洁地表达此式，在原坐标的基础上，引入第三个数值为1的坐标，这种表示方法称为齐次坐标，这样就可以用简单的矩阵乘法来表示仿射变换：

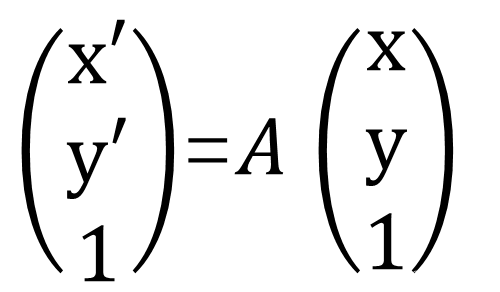
  通常称A为仿射变换矩阵，因为它的最后一行均为（0，0，1）。

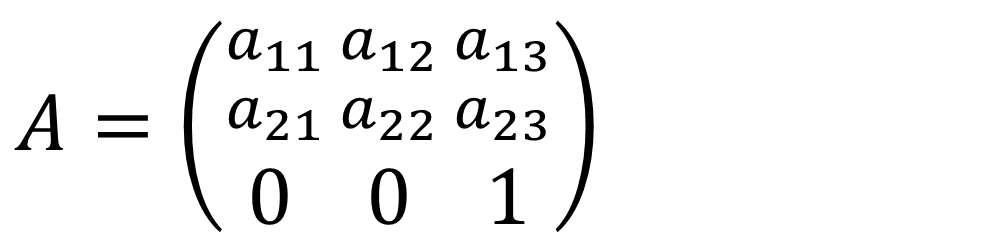
  为方便起见，在讨论过程中会省略最后一行。下面将详细介绍的仿射变换类型：平移、缩放、旋转。

  

2.1 平移

  平移是最简单的仿射变换，如下图矩形所示，假设将空间坐标(x,y)，其中0≤x≤110，0≤y≤110，先沿x轴正方向平移40，再沿y轴正方向平移50；或者反过来，先沿y轴正方向平移，再沿x轴正方向平移，平移后的坐标为(x',y') ，即(x',y')=(x+40，y+50)。

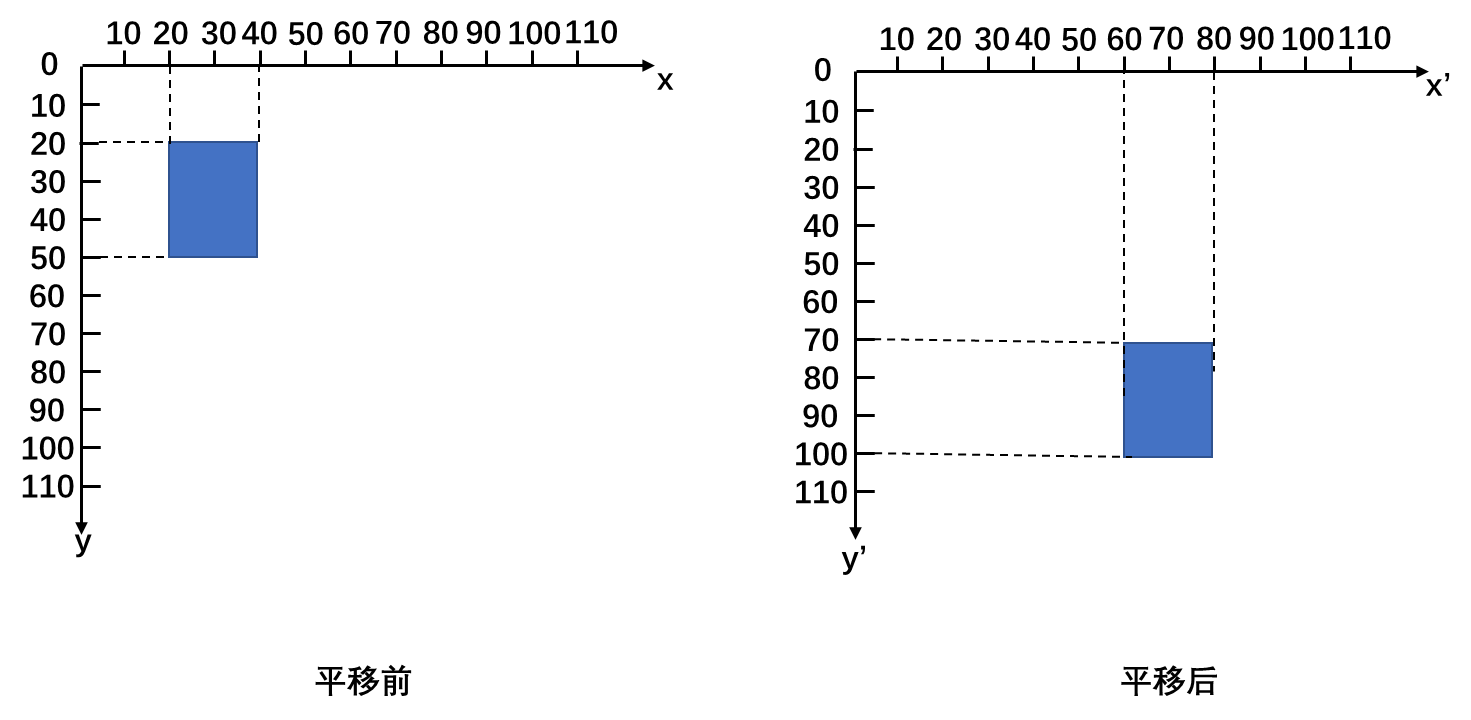
  关于平移，假设任意空间坐标(x,y)先沿x轴平移tx ，再沿y轴平移ty ，则最后得到的坐标为 (x',y')=(x+tx ，y+ty)。用矩阵形式表示该平移变换过程如下：

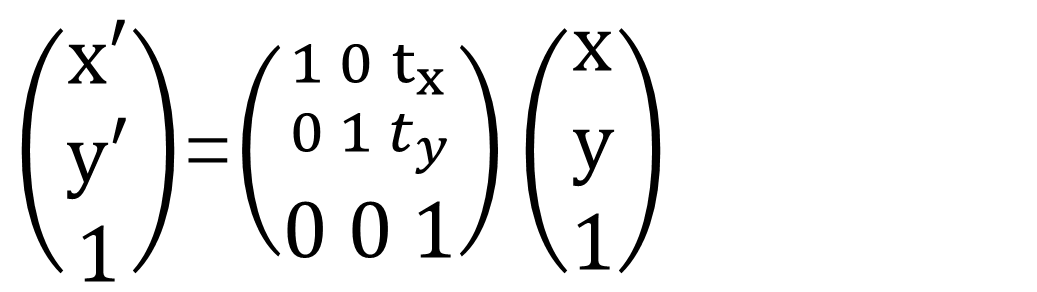
  其中，若tx>0，则表示沿x轴正方向移动；tx<0，则表示沿x轴负方向移动；ty亦是。

  

2.2 放大和缩小

  放大和缩小不是指在物理空间中某一个物体的放大和缩小。二维空间坐标(x,y)以(0,0)为中心在水平方向上缩放sx 倍，在垂直方向上缩放sy 倍，指的是变换后的坐标位置离(0,0)的水平距离变为原坐标离位置中心点的水平距离的sx 倍，垂直距离变为原坐标离中心点的垂直距离的sy 倍。
  根据以上定义，(x,y)以(0,0)为中心缩放变换后的坐标为(x',y')，即(x',y')=(sx*x，sy*y)，显然，变换
后的坐标位置离中心点的水平距离由|x|缩放为|sx*x|，垂直距离由|y|缩放为|sy*y|。
  若sx>1，则表示在水平方向上放大，就是离中心点的水平距离增大了；反之，在水平方向上缩小。同样，若sy>1，则表示在垂直方向上放大；反之，在垂直方向上缩小。
  通常令sx =sy ，即常说的等比例缩放。例如:(-10，10)以(0,0)为中心放大两倍，则坐标变换为(-20，20)。缩放变换也可用矩阵形式来表示：

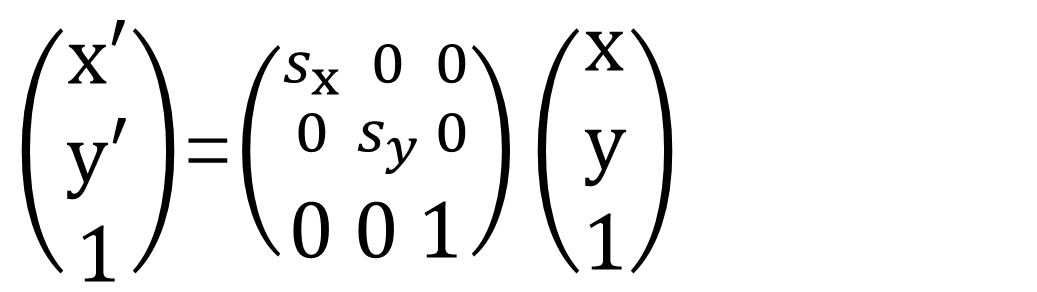
  如下图所示：

  以上介绍的是以原点(0，0)为中心的缩放变换，那么(x,y)以任意一点(x0,y0)为中心在水平方向上缩放sx倍，在垂直方向上缩放sy倍，则缩放后的坐标为(x',y')，即(x',y') =（x0 +sx*(x-x0)，y0 +sy*(y-y0)）。
  显然，缩放后的坐标位置离中心点的水平距离变为原来的sx 倍，离中心点的垂直距离变为原来的sy倍。可以将该变换过程理解为先将原点平移到中心点，再以原点为中心进行缩放，然后移回坐标原点。用矩阵形式可以表示为：

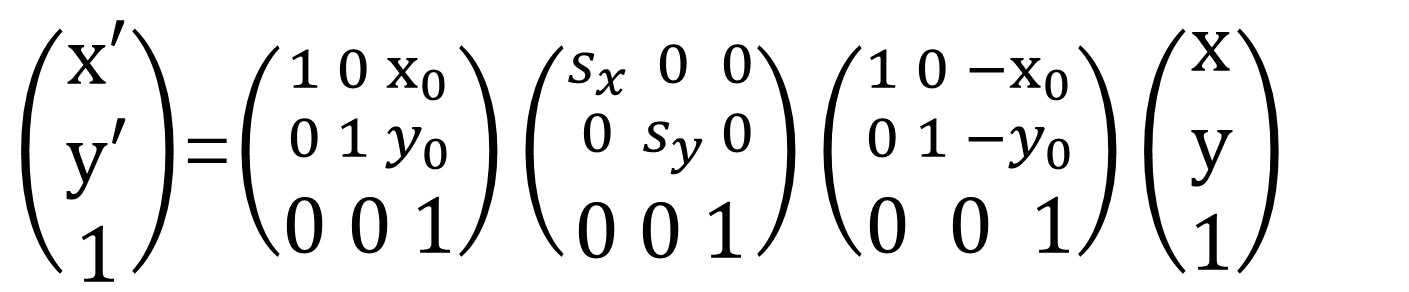
  这里显示了齐次坐标的优势，以任意一点为中心的缩放仿射变换矩阵是平移矩阵和以(0，0)为中心的缩放仿射变换矩阵组合相乘而得到的。

  我们通过一个实际案例来深入理解：上图中矩形右下角坐标(40,50)以(20,20)为中心同比例缩小2倍。(40,50)离(20,20)的水平距离为20，垂直距离为30，同比例缩小2倍，则变换后的坐标位置离(40,50)的水平距离应为10，垂直距离应为15，即变换后的坐标为(30，35)，用矩阵表示该计算过程为：

  

2.3 旋转

  除了坐标的平移、缩放，还有一种常用的坐标变换，即旋转。如下图所示，图1显示的是(x,y)绕(0,0)顺时针旋转α（α>0）的结果;图2显示的是(x,y)绕(0,0)逆时针旋转α的结果。

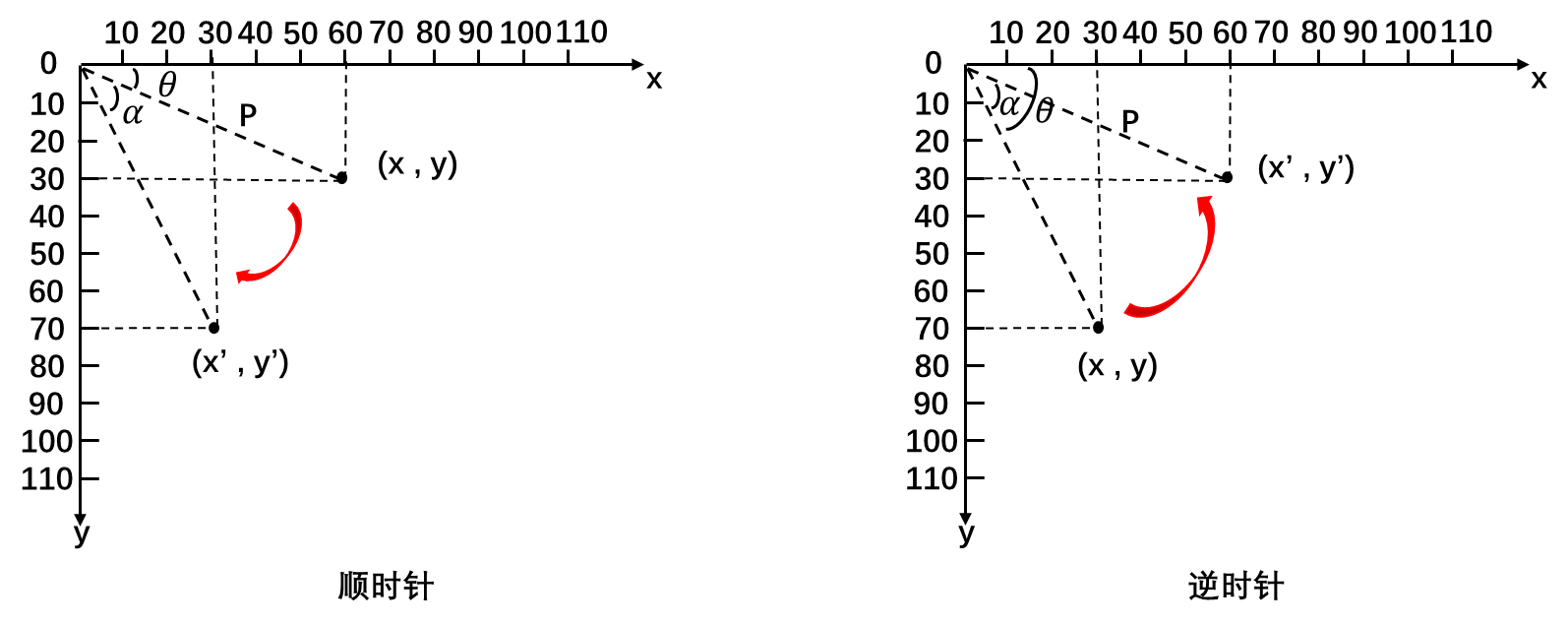
  对于顺时针后的坐标(x',y')：

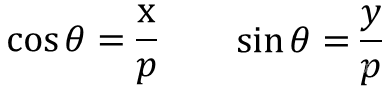
  其中p代表(x,y)到中心点(0,0)的距离，则:

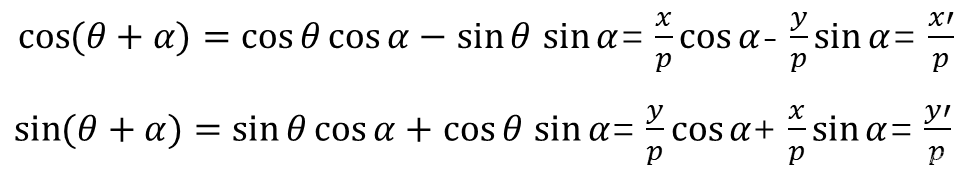
  化简得：

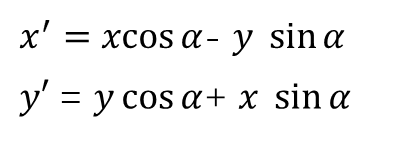
  那么，用矩阵表示为：

  对于逆时针后的坐标(x',y')：

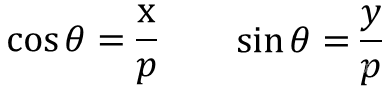
  化简得：

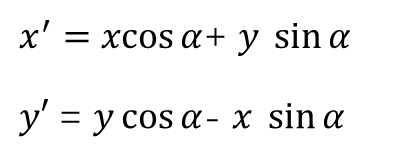
  那么，用矩阵表示为：

  从得到的两个旋转仿射矩阵可得逆时针旋转α和顺时针旋转-α是一样的，用程序实现时，实现其中的一种就可以了。
  以上讨论的旋转变换是以(0，0)为中心进行旋转的，如果(x，y)绕任意一点(x0，y0)逆时针旋转α，则首先将原点移到旋转中心，然后绕原点旋转，最后移回坐标原点，即：

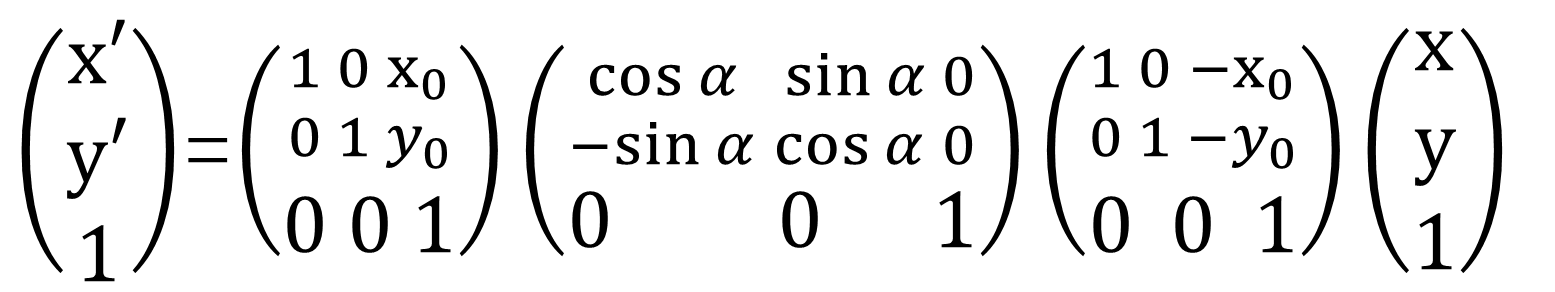
  需要注意的是，以上解决的是已知坐标及其仿射变换矩阵，从而计算出变换后的坐标。

  那么，反过来考虑一个问题，如何通过已知坐标及其对应的经过某种仿射变换后的坐标，从而计算出它们之间的仿射变换矩阵？

  

2.4 计算仿射矩阵

  对于空间变换的仿射矩阵有两种计算方式，分别是方程组法和矩阵相乘法。

  (1) 方程组法

  仿射变换矩阵有六个未知数，所以需要三组对应位置坐标，构造出由六个方程组成的方程组即可解六个未知数。
  举例：如果(0,0) 、(200,0) 、(0,200)这三个坐标通过某仿射变换矩阵A分别转换为(0,0) 、(100,0) 、(0,100)，则可利用这三组对应坐标构造出六个方程，求解出A。

  对于C++的API函数getAffineTransform()输入参数有两种方式，第一种方式是将原位置坐标和对应的变换后的坐标分别保存在Point2f数组中，代码如下：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include<opencv2/highgui/highgui.hpp>

using namespace std;
using namespace cv;
int main() {

	Point2f src[] = { Point2f(0,0),Point2f(200,0), Point2f(0,200) };
	Point2f dst[] = { Point2f(0,0),Point2f(100,0), Point2f(0,100) };

	Mat A = getAffineTransform(src,dst);

	cout << A<<endl;
	
	return 0;
}

  返回值A仍然是2行3列的矩阵，指的是仿射变换矩阵的前两行。需要注意的是，数据类型是CV_64F而不是CV_32F。

  
  第二种方式是将原位置坐标和对应的变换后的坐标保存在Mat中，每一行代表一个坐标，数据类型必须是CV_32F，否则会报错，代码如下：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include<opencv2/highgui/highgui.hpp>

using namespace std;
using namespace cv;
int main() {

	Mat src = (Mat_<float>(3, 2) << 0, 0, 200, 0, 0, 200);
	Mat dst = (Mat_<float>(3, 2) << 0, 0, 100, 0, 0, 100);


	Mat A = getAffineTransform(src, dst);
	cout << A << endl;

	return 0;
}

  (2) 矩阵相乘法

  使用矩阵相乘法计算仿射矩阵，前提是需要知道基本仿射变换步骤，即如果(x,y)先缩放再平移，则变换后的矩阵形式为：

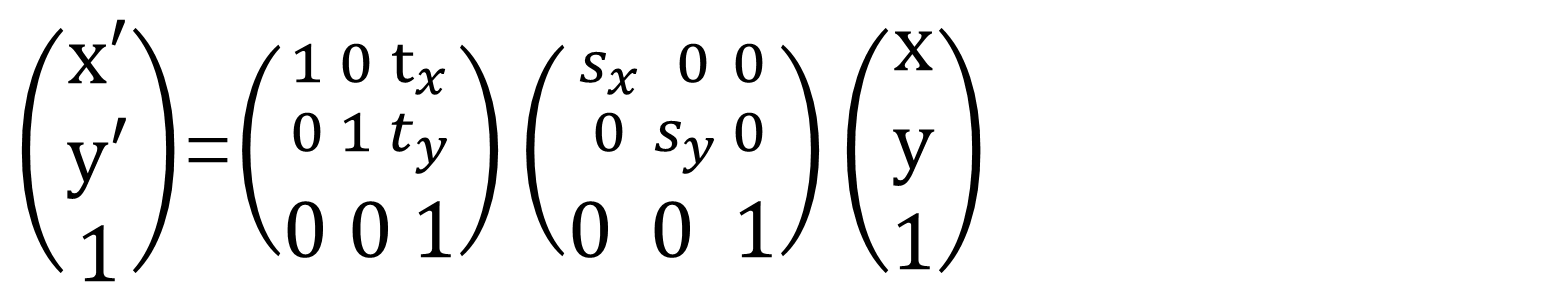
  以上仿射变换矩阵是由平移矩阵乘以缩放矩阵得到的。需要注意的是，虽然先缩放再平移，但是仿射变换矩阵是平移仿射矩阵乘以缩放仿射矩阵，而不是缩放仿射矩阵乘以平移仿射矩阵，即等式右边的运算是从右向左进行的。

  在2.2 OpenCV之矩阵运算详解(全)中已经提到，在OpenCV中是通过“*”运算符或者gemm函数来实现矩阵的乘法的，代码如下：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include<opencv2/highgui/highgui.hpp>

using namespace std;
using namespace cv;
int main() {
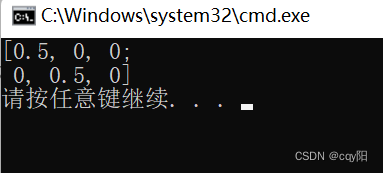
	Mat src = (Mat_<float>(3, 3) << 0.5, 0, 0, 0, 0.5, 0, 0, 0, 1);//缩放矩阵
	Mat dst = (Mat_<float>(3, 3) << 1, 0, 100, 0,1, 200, 0, 0, 1);//平移矩阵

	Mat A;

	gemm(src,dst,1.0,Mat(),0,A,0);

	cout << A << endl;

	return 0;
}

  类似的，如果以(x0,y0)为中心进行缩放变换，然后逆时针旋转α，则仿射变换矩阵为：

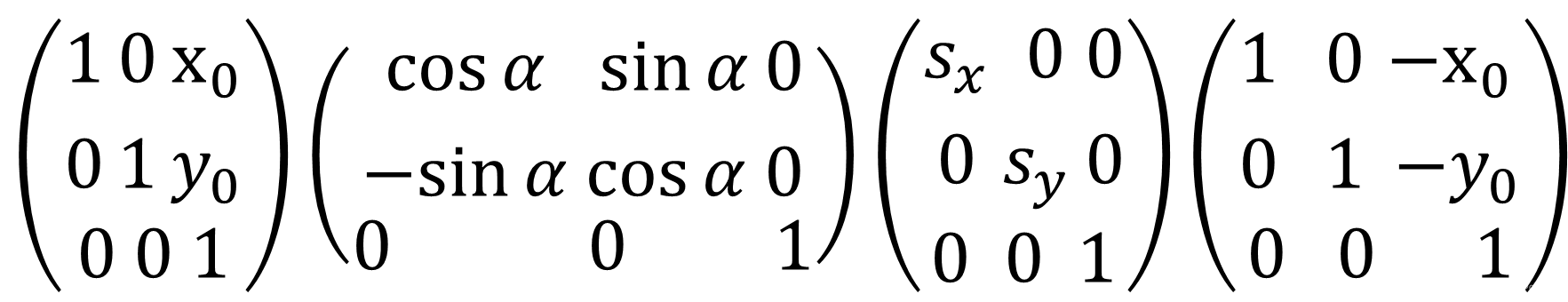
  即：

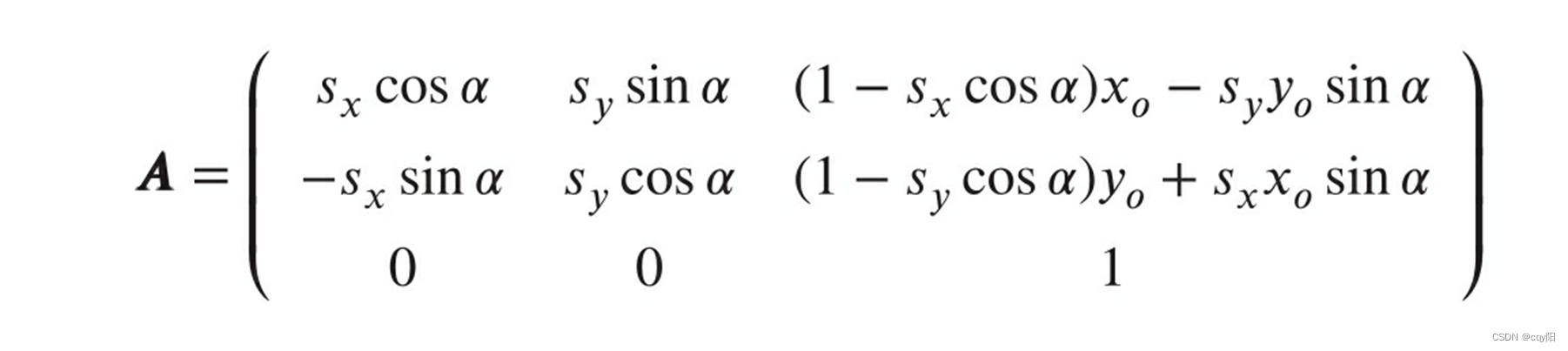
  若还需平移，则只需将结果左乘一个平移仿射矩阵即可。以上是以(x0,y0)为中心先进行缩放，然后逆时针旋转α的；反过来，如果先逆时针旋转α再进行缩放处理，则仿射变换矩阵为：

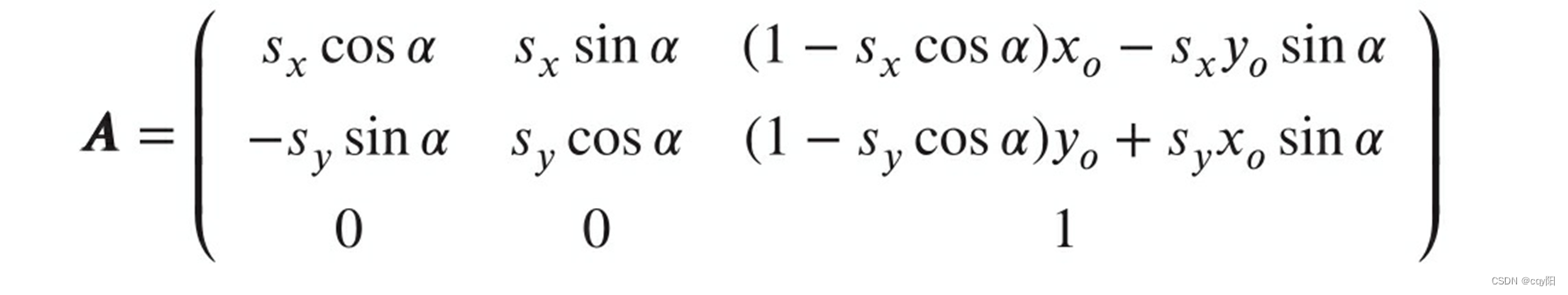
  从得到的两个仿射变换矩阵可以看出，如果是等比例缩放的，即sx =sy ，则两个仿射变换矩阵是相等的。对于这种等比例缩放的仿射变换，OpenCV提供了函数：

getRotationMatrix2D(center,angle,scale)

  其中参数center：变换中心点的坐标；
  scale：等比例缩放的系数；
  angle：逆时针旋转的角度。

  虽然这里angle称为逆时针，但是如果angle是负数，则相当于顺时针了。需要注意的是：angle是以角度为单位，而不是以弧度为单位的。

  举例：计算以坐标点(50,50)为中心逆时针旋转45°的仿射变换矩阵。

#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include<opencv2/highgui/highgui.hpp>

using namespace std;
using namespace cv;
int main() {
	Mat A = getRotationMatrix2D(Point2f(50, 50), 45, 0.5);

	cout << A << endl;
	return 0;
}

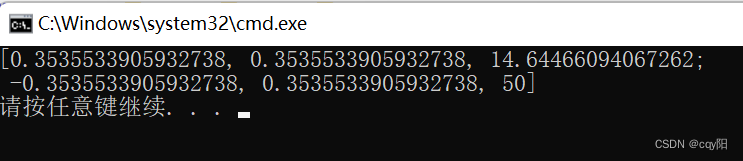
  返回值是一个2×3的Mat，数据类型是CV_64F。
  知道空间坐标变换中的仿射变换后，接下来需要考虑如何将其运用到图像的几何变换中，就需要利用以下提到的插值算法了。

  

2.5 插值算法

  (1) 最近邻插值法

  已知坐标点(x,y)，令[x]代表x的整数部分，[y]代表y的整数部分，如果x>0且y>0，即在第一象限，显然(x,y)的四个相邻整数坐标为([x]，[y])、([x]+1，[y])、([x]，[y]+1)、([x]+1，[y]+1)；如果在第二象限，即x<0且y>0，则(x,y)的四个相邻整数坐标为([x]，[y])、([x]-1，[y])、([x]，[y]+1)、([x]-1，[y]+1)；其他两个象限类似。

  举例：(2.3，2.7)的四个相邻整数坐标分别为(2，2)、(3，2)、(2，3)、(3，3)，离它最近的是(2，3)，则函数 fI 在(2.3，2.7)处的函数值等于 fI 在(2，3)处的值，即 fI (2.3，2.7)= fI (2，3)。

  使用最近邻插值法完成图像几何变换，输出图像会出现锯齿状外观，对图像放大处理的效果会更明显。为了得到更好的效果，应使用更多的信息，而不仅仅使用最近像素的灰度值，常用的方法是双线性插值和三次样条插值。

  (2) 双线性插值法

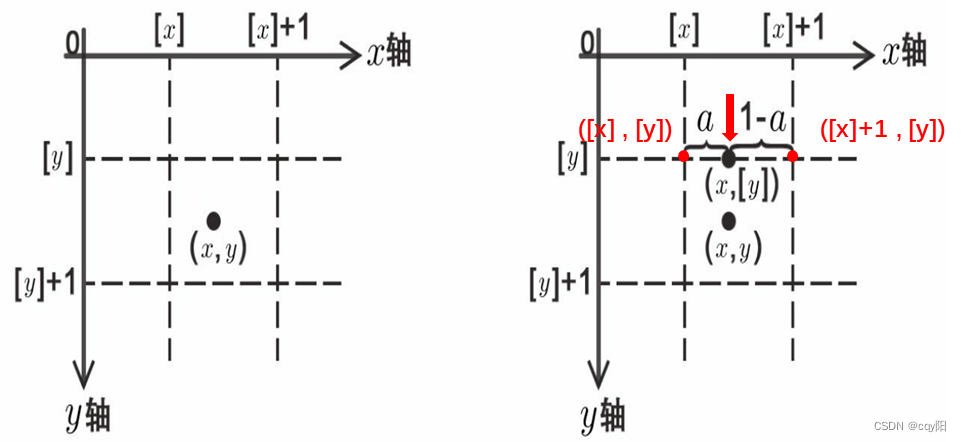
  对于双线性插值，以(x,y)落在第一象限为例，如下图所示，其他象限类似，处理过程可以分为以下三个步骤。

  第一步

  |x-[x]|是点(x,y)和([x]，[y])的水平距离，|[x]+1-x|是点(x,y)和([x]+1，[y])的水平距离，显然0<|x-[x]|<1，0<|[x]+1-x|<1且|x-[x]|+|[x]+1-x|=1。为了方便，记a=|x-[x]|，如下图所示，通过以下线性关系估计 fI 在(x,[y])处的值：

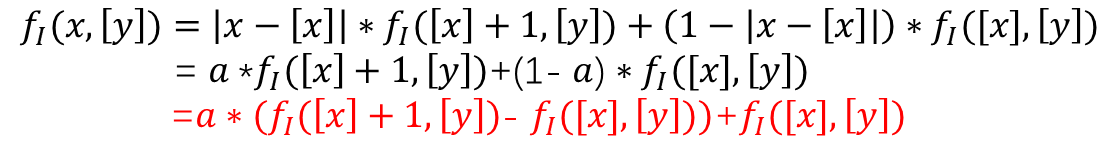
  第二步

  和第一步类似，|x-[x]|是点(x，y)和([x]，[y]+1)的水平距离，|[x]+1-x|是点(x，y)和([x]+1，[y]+1)的水平距离，如下图所示，通过以下线性关系估计fI 在(x,[y]+1)处的值处的值：

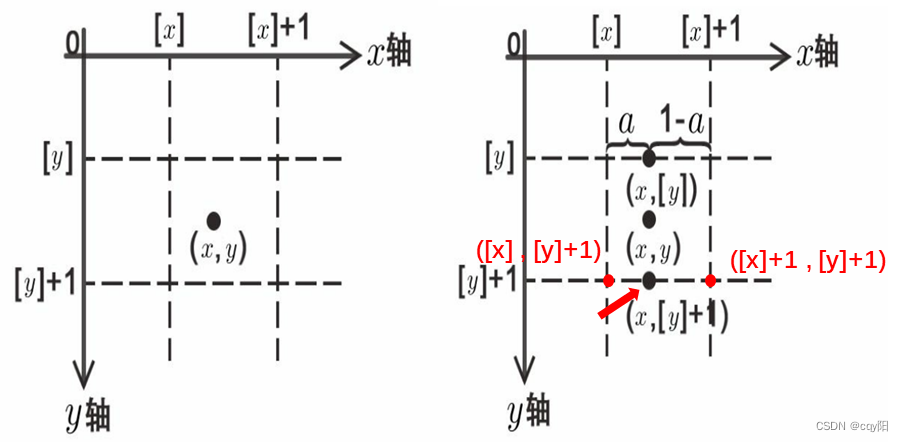
  第三步

  通过第一步和第二步分别得到了fI 在(x，[y]+1)和(x，[y])处的函数值，(x,y)和(x，[y])的垂直距离|y-[y]|，(x,y)和(x，[y]+1)处的垂直距离为|[y]+1-y|，如下图所示，通过以下线性关系估计fI 在(x,y)处的函数值：

  令b=|y-[y]|：

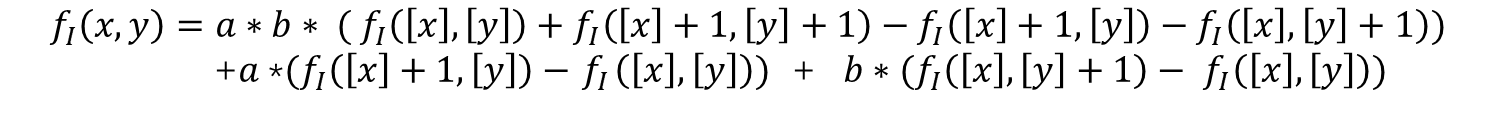
  这样对于非整数坐标处的函数值，就可以利用它的邻域的四个整数坐标处的函数值进行插值计算而得到。如果先进行两次垂直方向上的插值，然后再进行水平方向上的插值，得到的结果是一样的。

  从双线性插值法的公式可以看出，fI 是一个二阶的函数。有时为了得到更好的拟合值，需要高阶的插值函数，如三次样条插值、Legendre中心函数和sin(axs)函数，高阶插值常使用二维离散卷积运算来实现 。关于二维离散卷积将在后期会详细介绍。

  

2.6 代码实现

  关于几何变换OpenCV提供了几个方便简洁的函数。

  (1) 缩放

  前面已经详细介绍了关于图像几何变换的两个重要关键点：空间坐标变换和插值方法，在已知仿射变换矩阵的基础上，C++提供了warpAffine()函数。
  使用函数warpAffine()对图像进行缩放，需要先创建缩放仿射矩阵。为了使用更方便，对于图像的缩放，OpenCV还提供了另一个函数：

void resise(InputArayy src, OuputArray dst, Size dsize, double fx=0, double fy=0, int iterpolation=INTER_ LINEAR )

  src：输入图像矩阵；
  dst：输出图像矩阵;
  dsize：二元元组(宽，高)，输出图像大小；
  fx：在水平方向的缩放比例，默认0；
  fy：在垂直方向的缩放比例，默认0；
  interpolation：插值方法：INTE_NEAREST , INTE_LINEAR(默认)。

  这样在对图像矩阵进行缩放时，就不需要先创建缩放仿射矩阵，然后再使用函数warpAffine()了，在本质上resize的参数fx和fy也相当于构建了缩放仿射矩阵。下面分别使用这两个函数进行图像缩放：

#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include<opencv2/highgui/highgui.hpp>

using namespace std;
using namespace cv;
int main() {
Mat image = imread("D:/VSCodeFile/OpenCV_CSDN/image/logo.jpeg", IMREAD_COLOR);
	if (!image.data)
	{
		cout << "Image is not exist!";
	}

	/*第一种方式:利用warpAffine()进行缩放*/
	Mat dst1;
	Mat A = (Mat_<float>(2, 3) << 2, 0, 0, 0, 2, 0);//缩放矩阵
	warpAffine(image,dst1,A,Size(2*image.cols,2*image.rows));

	/*第二种方式:利用resize()进行缩放*/
	Mat dst2;

	resize(image,dst2, Size(image.cols*2, image.rows *2),2,2);

	imshow("src", image);
	imshow("warpAffine", dst1);
	imshow("resize", dst2);
	waitKey(0);
	
	return 0;
}

  对图像进行缩放处理时，从代码量来说，使用resize会更方便。

  
  (2) 旋转

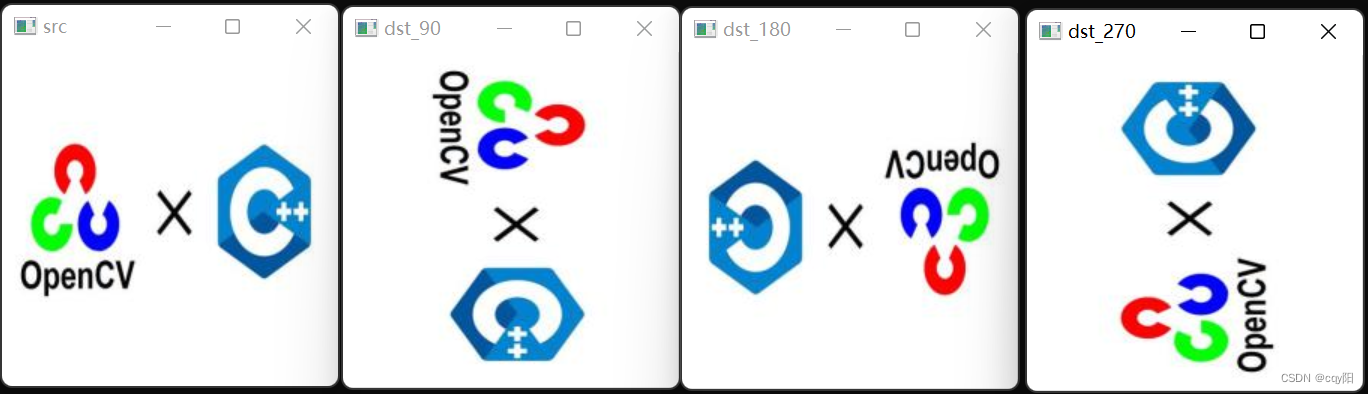
  在OpenCV中，定义了rotate()函数来实现图像矩阵顺时针旋转90°、180°、270°，函数如下：

rotate(InputArray src,OutputArray dst,int rotateCode)

  src：输入图像矩阵(单、多通道均可)；
  dst：输出图像矩阵；
  rotateCode：ROTATE_90_CLOCKWISE：顺时针旋转90°；ROTATE_180：顺时针旋转180°；ROTATE_90_COUNTERCLOCKWISE：顺时针旋转270°；

  注意：虽然是图像矩阵的旋转，但该函数不需要利用仿射变换来完成这类旋转，只是行列的互换，类似于矩阵的转置操作，所以该函数声明在头文件opencv2/core.hpp中。

#include <iostream>
#include <opencv2/opencv.hpp>
#include <opencv2/core/core.hpp>
#include<opencv2/highgui/highgui.hpp>

using namespace std;
using namespace cv;
int main() {
	//旋转函数rotate

	Mat image = imread("D:/VSCodeFile/OpenCV_CSDN/image/logo.jpeg", IMREAD_COLOR);
	Mat dst_90;
	Mat dst_180;
	Mat dst_270;

	imshow("src", image);//原图显示

	rotate(image,dst_90,ROTATE_90_CLOCKWISE);
	imshow("dst_90", dst_90);//顺时针90°

	rotate(image, dst_180, ROTATE_180);
	imshow("dst_180", dst_180);//顺时针180°

	rotate(image, dst_270, ROTATE_90_COUNTERCLOCKWISE);
	imshow("dst_270", dst_270);//顺时针270°

	waitKey(0);
	return 0;
}

在这里插入图片描述

三、 总结

  最后，长话短说，大家看完就好好动手实践一下，切记不能三分钟热度、三天打鱼，两天晒网。OpenCV是学习图像处理理论知识比较好的一个途径，大家也可以自己尝试写写博客，来记录大家平时学习的进度，可以和网上众多学者一起交流、探讨，有什么问题希望大家可以积极评论交流，我也会及时更新，来督促自己学习进度。希望大家觉得不错的可以点赞、关注、收藏。

🚶🚶🚶 今天的文章就到这里啦~
喜欢的话，点赞👍、收藏⭐️、关注💟哦 ~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/128380.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

CSS 颜色

CSS 颜色

文章目录CSS 颜色关键字 & 十六进制 & RGBopacity 透明度RGBA 颜色CSS3 渐变线性渐变径向渐变CSS 颜色 关键字 & 十六进制 & RGB W3C十六色 opacity 透明度 语法 opacity: 数值;说明 在CSS3中&#xff0c;我们可以使用opacity属性来定义元素的透明度。 o…
阅读更多...
excel排序求和：如何统计前几名数据合计 下篇

excel排序求和：如何统计前几名数据合计 下篇

上次咱们说到一个公式SUM(LARGE(B:B,ROW(INDIRECT("1:"&H2))))&#xff0c;其中的ROW(INDIRECT("1:"&H2))这部分如果写成ROW(1:H2)就会报错&#xff1a; 原因也告诉大家了&#xff0c;就是ROW函数的参数只能使用单元格或单元格区域。 因此解决的办…
阅读更多...
Java IO流 - 字节流的使用详细介绍

Java IO流 - 字节流的使用详细介绍

文章目录IO流的基本介绍字节流的使用文件字节输入流创建字节输入流每次读取一个字节每次读取一个数组一次读取全部字节文件字节输出流创建字节输出流写入文件输出流文件拷贝练习IO流的基本介绍 IO流的概述: I 表示intput&#xff0c;是数据从硬盘文件读入到内存的过程&#xf…
阅读更多...
频谱分析仪关键性能指标

频谱分析仪关键性能指标

频谱分析仪关键性能指标 频谱分析仪作为分析仪表&#xff0c;其基本性能要求包含&#xff1a; 1. 频率方面指标&#xff1a; 测量频率范围&#xff1a;反映频谱仪测量信号范围能力; 频率分辨率&#xff1a;反映频谱仪分辨两个频率间隔信号的能力。 2. 幅方面度指标&#x…
阅读更多...
银河麒麟（aarch64）安装Qt，报错main.cpp:8:5: error: unknown type name ‘MainWindow‘...

银河麒麟（aarch64）安装Qt，报错main.cpp:8:5: error: unknown type name ‘MainWindow‘...

环境&#xff1a; 版本&#xff1a;银河麒麟桌面操作系统V10&#xff08;SP1&#xff09; 内核&#xff1a;Linux 5.4.18-35-generic CPU&#xff1a;Phytium&#xff0c;D2000/8 终端输入 uname -m 查看 架构 aarch64 在商店安装Qt&#xff0c; 安装完成后 工具-选项-kits构…
阅读更多...
SAP ABAP——SAP简介（五）【ABAP的前世今生和未来】

SAP ABAP——SAP简介（五）【ABAP的前世今生和未来】

&#x1f482;作者简介&#xff1a; THUNDER王&#xff0c;一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学会计学专业大二本科在读&#xff0c;同时任汉硕云&#xff08;广东&#xff09;科技有限公司ABAP开发顾问。在学习工作中&#xff0c;我通常使用偏后…
阅读更多...
kali安装cobaltstrike详细教程

kali安装cobaltstrike详细教程

下载cobaltstrike-linux版本，此下载链接提供4.3，4.4，4.5三个版本https://download.csdn.net/download/weixin_59679023/87354658 xshell上传至kali,解压 unzip cobaltstrike 进入cobaltstrike目录，ls查看如下 ls 给cs的服务端teamserver和客户端start.sh执行权限 chmod …
阅读更多...
【计算机图形学入门】笔记8：Shading 2着色（着色频率、图形管线、纹理映射）

【计算机图形学入门】笔记8：Shading 2着色（着色频率、图形管线、纹理映射）

08Shading 2着色&#xff08;着色频率、图形管线、纹理映射&#xff09;前置知识1.Specular Term 高光2.Ambient Term 环境光照项3.最终的成像公式2.着色频率1.Flat shading2.Gouraud shading3.Phong shading4.那么如何计算逐顶点法线&#xff1f;5.如何定义逐像素的法线&#…
阅读更多...
微信小程序之后台交互--首页

微信小程序之后台交互--首页

目录一、后台准备1、application.yml2、generatorConfig.xml3、WxHomeController4、MinoaApplication.java二、小程序首页动态数据加载及优化1、config/app.js2、util.js3、index.wxml4、index.js5、page.wxs一、后台准备 1、application.yml spring:datasource:#type连接池类…
阅读更多...
冰冰学习笔记：管道与共享内存

冰冰学习笔记：管道与共享内存

欢迎各位大佬光临本文章&#xff01;&#xff01;&#xff01; 还请各位大佬提出宝贵的意见&#xff0c;如发现文章错误请联系冰冰&#xff0c;冰冰一定会虚心接受&#xff0c;及时改正。 本系列文章为冰冰学习编程的学习笔记&#xff0c;如果对您也有帮助&#xff0c;还请各位…
阅读更多...
直播榜单正式上线，超店有数让你数秒内找到热卖直播间和高转化带货达人

直播榜单正式上线，超店有数让你数秒内找到热卖直播间和高转化带货达人

众所周知&#xff0c;国内抖音直播带货正处于火爆的状态&#xff0c;大部分电商商家都在抖音通过直播带货实现流量变现。那么TikTok作为国内抖音复制到海外的短视频App&#xff0c;是全球最火爆的App之一&#xff0c;被视为品牌出海的新风口。它的直播变现模式也和抖音大同小异…
阅读更多...
ThinkPHP 路由使用

ThinkPHP 路由使用

最近在使用ThinkPHP6做项目的开发&#xff0c;故整理了一些常用的路由使用方式&#xff0c; 可以方便之后的使用。 目录 引用路由门面 基础路由 快捷路由 规则表达式 静态地址 静态结合动态地址 方法设置 完全匹配 默认路由规则 设置完全匹配 路由别名 变量规则 局…
阅读更多...
再次飙升GitHub榜首？这份“保姆级”的SpringBoot笔记，不服不行

再次飙升GitHub榜首？这份“保姆级”的SpringBoot笔记，不服不行

Spring Boot 延续了 Spring 框架的核心思想 IOC 和 AOP&#xff0c;简化了应用的开发和部署&#xff0c;通过少量的代码就能创建一个独立的、产品级别的 Spring 应用。在继承了Spring 一切优点的基础上&#xff0c;其最大的特色就是简化了Spring 应用的集成、配置、开发&#x…
阅读更多...
怎样提高美国独立服务器的安全性？

怎样提高美国独立服务器的安全性？

目前&#xff0c;越来越多的用户都开始使用起了美国独立服务器&#xff0c;而这种服务器通常都比共享服务器的安全性要高出许多&#xff0c;但是管理起来比较复杂。下面将为大家介绍怎样才能提高美国独立服务器的安全性&#xff0c;包括下面几点&#xff1a; 1.使用强密码 有时…
阅读更多...
队列------数据结构

队列------数据结构

队列:Queue是一个普通的队列&#xff0c;Deque是一个双端队列 普通的队列:只能是队尾进&#xff0c;队头出; 双端队列:可以从队头进队尾出&#xff0c;也可以从队尾进&#xff0c;队头出&#xff0c;也可以用作一个栈; 1)下面我们来介绍一下Queue的实现方法: 在有容量限制的情况…
阅读更多...
你是真的“C”——详解函数递归

你是真的“C”——详解函数递归

详解函数递归运用&#x1f60e;前言&#x1f64c;一、什么是递归&#x1f64c;二、递归运用的两个必要条件&#x1f64c;三、递归与迭代&#x1f64c;总结撒花&#x1f49e;哈喽&#xff01;&#x1f604;各位CSDN的uu们&#xff0c;我是你的博客好友小梦&#xff0c;希望我的文…
阅读更多...
长安链 VM Engine架构设计深度解读

长安链 VM Engine架构设计深度解读

VM Engine是长安链智能合约引擎的推荐选型&#xff0c;采用Docker容器化架构&#xff0c;容器内部由一个任务调度器和多个合约进程组成&#xff0c;实现了多合约隔离与多进程并发&#xff0c;支持独立部署&#xff0c;目前支持Golang语言合约。 1. 背景说明 自2009年11月以来&…
阅读更多...
CUDA 冬令营1

CUDA 冬令营1

基本概念 1.CPU的任务&#xff1a;为串行任务优化 2.GPU的任务&#xff1a;为并行任务优化 3.L4T ubuntu&#xff1a;基于NVIDIA Tegra芯片的ubuntu系统&#xff08;linux for Tegra&#xff09; 4.Tegra&#xff1a;继承了ARM CPU 和 NVIDIA GPU的处理器芯片 5.X86&#xff1…
阅读更多...
2023京东年货节全民炸年兽活动最详细规则

2023京东年货节全民炸年兽活动最详细规则

2023京东全民炸年兽活动规则 1、活动时间 整体活动时间: 2022年12月26日00: 00: 00–2023年01月15日23: 59: 59 2、活动玩法 (1)玩法一:全民炸年兽瓜分10亿压岁钱 活动时间: 2022年12月26日00: 00: 00–2023年01月15日23: 59: 59 (2) 玩法二:每晚8点分百万红包 活动时间…
阅读更多...
Houdini和C4D区别在哪？哪个更好用

Houdini和C4D区别在哪？哪个更好用

Houdini和C4D作为当前软件市场上非常热门的设计软件&#xff0c;现在越来越多的小伙伴开始学习。所以咱们今天就从行业应用、建模、动画和使用难易度等进行多方面对比&#xff0c;帮助小伙伴们更清楚地了解这两款软件—— Houdini作为一款非常受欢迎的3D&VFX制作工具&#…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023