本文会系统性的介绍算法的概念、复杂度,后续会更新算法思想以及常见的失效算法、限流算法、调度算法、定时算法等,辅助大家快速学习算法和数据结构知识。
概念
数据结构
概述
数据结构是计算机存储、组织数据的方式。数据结构是指相互之间存在一种或多种特定关系的数据元素的集合。通常情况下,精心选择的数据结构可以带来更高的运行或者存储效率。
划分
从关注的维度看,数据结构可以划分为数据的逻辑结构和物理结构,同一逻辑结构可以对应不同的存储结构。
逻辑结构反映的是数据元素之间的逻辑关系,逻辑关系是指数据元素之间的前后间以什么形式相互关联,这与他们在计算机中的存储位置无关。逻辑结构包括:
- 集合:只是扎堆凑在一起,没有互相之间的关联
- 线性结构:一对一关联,队形
- 树形结构:一对多关联,树形
- 图形结构:多对多关联,网状
数据物理结构指的是逻辑结构在计算机存储空间中的存放形式(也称为存储结构)。一般来说,一种数据结构的逻辑结构根据需要可以表示成多种存储结构,常用的存储结构有顺序存储、链式存储、索引存储和哈希存储等。
- 顺序存储:用一组地址连续的存储单元依次存储集合的各个数据元素,可随机存取,但增删需要大批移动
- 链式存储:不要求连续,每个节点都由数据域和指针域组成,占据额外空间,增删快,查找慢需要遍历
- 索引存储:除建立存储结点信息外,还建立附加的索引表来标识结点的地址。检索快,空间占用大
- 哈希存储:将数据元素的存储位置与关键码之间建立确定对应关系,检索快,存在映射函数碰撞问题
程序中常见的数据结构
- 数组(Array):连续存储,线性结构,可根据偏移量随机读取,扩容困难
- 栈( Stack):线性存储,只允许一端操作,先进后出,类似水桶
- 队列(Queue):类似栈,可以双端操作。先进先出,类似水管
- 链表( LinkedList):链式存储,配备前后节点的指针,可以是双向的
- 树( Tree):典型的非线性结构,从唯一的根节点开始,子节点单向执行前驱(父节点)
- 图(Graph):另一种非线性结构,由节点和关系组成,没有根的概念,互相之间存在关联
- 堆(Heap):特殊的树,特点是根结点的值是所有结点中最小的或者最大的,且子树也是堆
- 散列表(Hash):源自于散列函数,将值做一个函数式映射,映射的输出作为存储的地址
算法
算法指的是基于存储结构下,对数据如何有效的操作,采用什么方式可以更有效的处理数据,提高数据运算效率。数据的运算是定义在数据的逻辑结构上,但运算的具体实现要在存储结构上进行。一般涉及的操作有以下几种:
- 检索:在数据结构里查找满足一定条件的节点。
- 插入:往数据结构中增加新的节点,一般有一点位置上的要求。
- 删除:把指定的结点从数据结构中去掉,本身可能隐含有检索的需求。
- 更新:改变指定节点的一个或多个字段的值,同样隐含检索。
- 排序:把节点里的数据,按某种指定的顺序重新排列,例如递增或递减
复杂度
时间复杂度
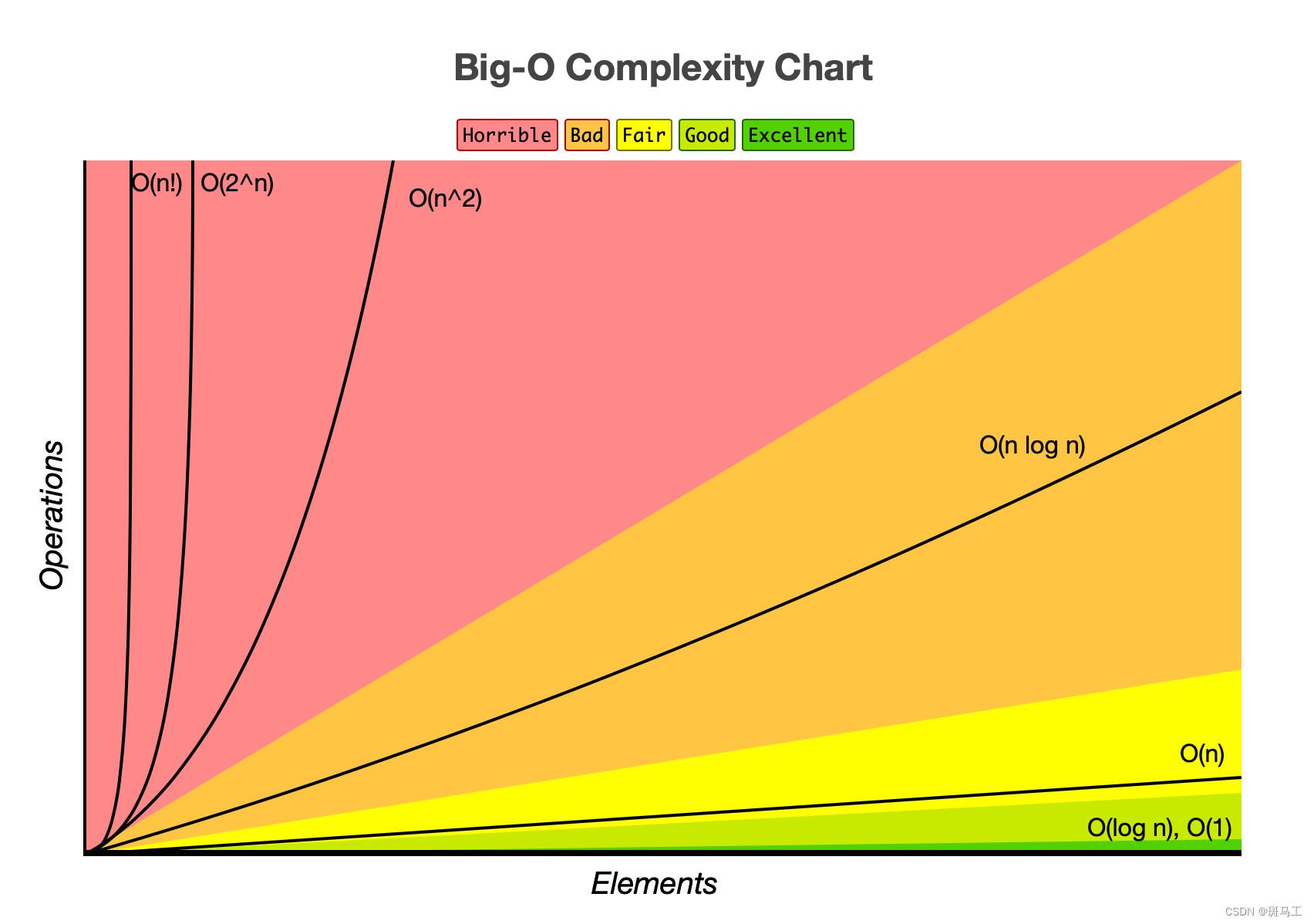
简单理解,为了某种运算而花费的时间,使用大写O表示。一般来讲,时间是一个不太容易计量的维度,而为了计算时间复杂度,通常会估计算法的操作单元数量,而假定每个单元运行的时间都是相同的。因此,总运行时间和算法的操作单元数量一般来讲成正比,最多相差一个常量系数。一般来讲,常见时间复杂度有以下几种:
- 常数阶O(1):时间与数据规模无关,如交换两个变量值
int i=1,j=2,k
k=i;i=j;j=k;
- 线性阶O(n):时间和数据规模呈线性,可以理解为n的1次方,如单循环里的操作
for(i=1;i<=n;i++){
do();
}
- k次方阶O(nk):执行次数是数量的k次方,如多重循环,以下为2次方阶实例
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
do();
}
}
- 指数阶O(2n):随着n的上升,运算次数呈指数增长
for(i=1;i<= 2^n;i++){
do();
}
- 对数阶O(log2n):执行次数呈对数缩减,如下
for(i=1;i<=n;){
i=2^i;
do();
}
- 线性对数阶O(nlog2n):在对数阶的基础上,进行线性n倍乘积
for(i=1;i<=2^n;i++){
for(j=1;j<=n;j++){
do();
}
}
- 总结
时间复杂度由小到大依次为:Ο(1)<Ο(log2n)<Ο(n)<Ο(nlog2n)<Ο(n2)<…<Ο(nk)<Ο(2n)<Ο(n!)
空间复杂度
与时间复杂度类似,空间复杂度是对一个算法在运行过程中占用内存空间大小的度量。一个程序执行时除了需要存储空间和存储本身所使用的指令、常数、变量和输入数据外,还需要一些对数据进行操作的辅助空间。而空间复杂度主要指的是这部分空间的量级。
- 固定空间:主要包括指令空间、常量、简单变量等所占的空间,这部分空间的大小与运算的数据多少无关,属于静态空间。
- 可变空间:主要包括运行期间动态分配的临时空间,以及递归栈所需的空间等,这部分的空间大小与算法有很大关系。
同样,空间复杂度也用大写O表示,相比时间复杂度场景相对简单,常见级别为O(1)和O(n),以数组逆序为例,两种不同算法对复杂度影响如下:
- O(1):常数阶,所占空间和数据量大小无关
//定义前后指针,和一个临时变量,往中间移动
//无论a多大,占据的临时空间只有一个temp
int[] a={1,2,3,4,5};
int i=0,j=a.length‐1;
while (i<=j){
int temp = a[i];
a[i]=a[j];
a[j]=temp;
i++;
j‐‐;
}
- O(n):线性阶,与数据量大小呈线性关系
//定义一个和a同等大小的数组b,与运算量a的大小呈线性关系
//给b赋值时,倒序取a
int[] a={1,2,3,4,5};
int[] b=new int[a.length];
for (int i = 0; i < a.length; i++) {
b[i]=a[a.length‐1‐i];
}
类比
对于一个算法,其时间复杂度和空间复杂度往往是相互影响的。时间复杂度低可能借助占用大的存储空间来弥补,
反之,某个算法所占据空间小,那么可能就需要占用更多的运算时间。两者往往需要达到一种权衡。
在特定环境下的业务,还需要综合考虑算法的各项性能,如使用频率,数据量的大小,所用的开发语言,运行的机
器系统等。两者兼顾权衡利弊才能设计出最适合当前场景的算法。
| 排序法 | 平均时间 | 最差情形 | 稳定度 | 额外空间 | 备注 |
|---|---|---|---|---|---|
| 冒泡 | O(n2) | O(n2) | 稳定 | O(1) | n小时较好 |
| 交换 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 选择 | O(n2) | O(n2) | 不稳定 | O(1) | n小时较好 |
| 插入 | O(n2) | O(n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 基数 | O(logRB) | O(logRB) | 稳定 | O(n) | B是真数(0-9),R是基数(个十百) |
| Shell | O(nlogn) | O(n2) | 稳定 | O(1) | 大部分已排序时较好 |
| 快速 | O(nlogn) | O(nlogn) | 不稳定 | O(nlogn) | n大时较好 |
| 归并 | O(nlogn) | O(nlogn) | 稳定 | O(1) | n大时较好 |
| 堆 | O(nlogn) | O(nlogn) | 不稳定 | O(1) | n大时较好 |