[PyTorch][chapter 4][李宏毅深度学习][Gradient Descent]

前言：

1: 梯度下降原理

2: 常见问题

3：梯度更新方案

4：梯度下降限制

一梯度下降原理

机器学习的目标找到最优的参数,使得Loss 最小

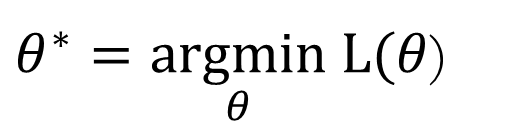
为什么顺着梯度方向loss 就能下降了。主要原理是泰勒公式。

假设损失函数为 $h(x)$

$h(x_{t+1})=h(x_t)+h^{'}(x_t)(x_{t+1}-x_t)+\frac{h^{"}(x_t)(x_{t+1}-x_t)^2}{2}+...$

忽略二阶导数, 当 $x_{t+1}-x_t=-h^{'}(x_t)$ 时候

$h(x_{t+1})=h(x_t)-h^{'}(x_t)^2 \leq h(x_t)$

因为要考虑二阶导数，所以损失函数一般都选凸函数,二阶为0,一阶导数有驻点的函数.

二常见问题

1：学习率learning rate

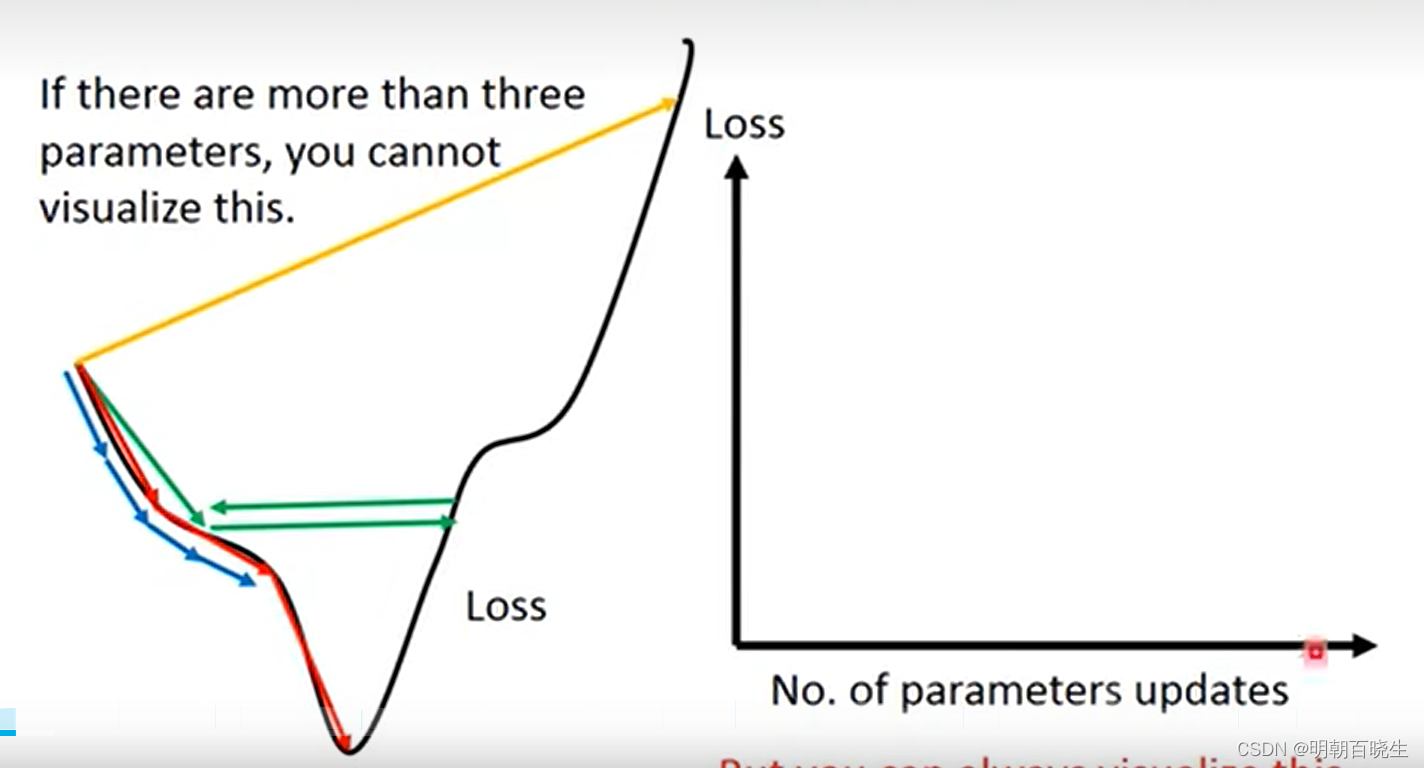
红线：学习率太小，收敛速度非常慢

绿线 : 学习率太大，无法收敛.

有什么自动调整学习率的算法？

三梯度更新方案

3.1 vanilla gradient descent

$\eta^{t}=\frac{\eta}{\sqrt{t+1}}$

学习率除以时间的开方：

训练开始：loss 远离极小值点,所以使用大的学习率
几次迭代后，我们接近极小值点，所以使用小的学习率

3.2 Adagrad

不同参数不同的学习率,设置不同的学习率,假设w 是权重系数里面的一个参数。

$w^{t+1}=w^t-\frac{\eta^t}{\sigma^t}g^t$

$=w^t-\frac{\eta}{\sqrt{\sum_{i=0}^{t}(g^i)^2}}g^t$

其中

$\eta^{t}=\frac{\eta}{\sqrt{t+1}}$

$\sigma^t=\sqrt{\frac{1}{t+1}\sum_{i=0}^{t}(g^i)^2}$

例：

为什么要不同参数设置不同的学习率：

如下图，不同维度的梯度是不一样的，如果使用同一个学习率会使得

某些维度出现学习率过大或者过小问题，导致收敛速度过慢或者网络震荡问题.

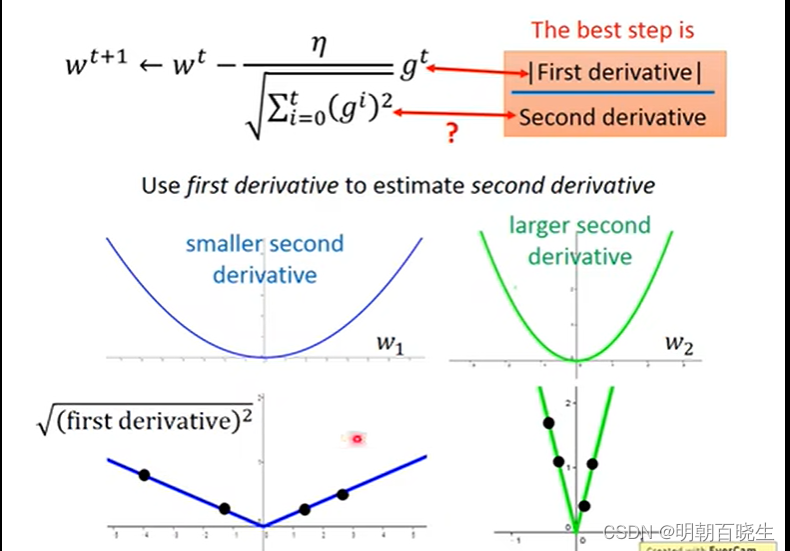
问题2：为什么要除以 $\sqrt{\sum_{i=0}^{t}(g^i)^2}$

这个参数相当于二次微分。

如下图：

一次微分小的我们希望学习率大一点，能够快速收敛.

一次微分大的我们希望其学习率小一点,防止网络震荡.

我们通过采样历史微分结果相加，学习率除以该参数就达到该效果。

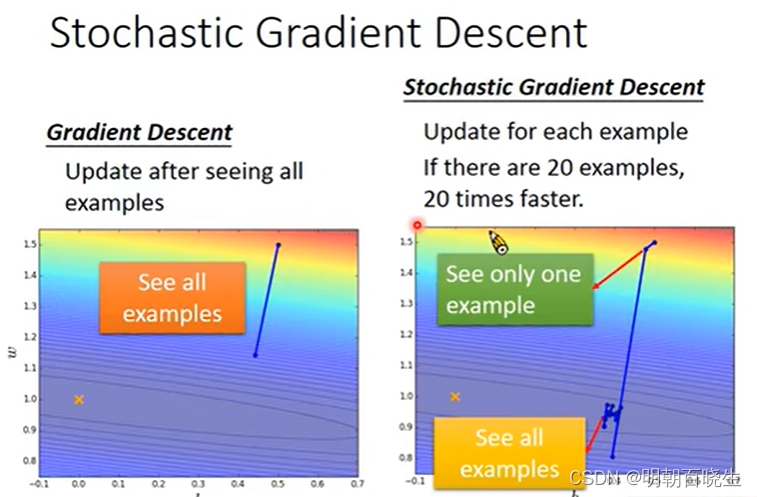
3.3 stochastic gradient descent(随机梯度下降法)

假设我们有20个样本

每轮迭代：

梯度下降法：计算20个样本,计算20个样本的梯度，通过平均值更新梯度

随机梯度下降法：随机选取一个样本，计算1个样本梯度，更新梯度

优点：速度快

3.4 batchnormalization

作用：

使得不同维度上面数据分布一致。

常用方案 batchnormalization：

数据集假设有m个样本,每个数据的维度为n

$\begin{bmatrix} x_1^1 & x_2^1 &... &x_n^1 \\ x_1^2 & x_2^2 &... &x_n^2 \\ & & & \\ x_1^m & x_2^m &... &x_n^m \end{bmatrix}$

对每个维度求其均值 $u_i,$ ,以及方差 $\sigma_i$ ，

$x_i^{r}=\frac{x_i^{r}-u_i}{\sigma_i}$

如下图： $y=w_1x_1+w_2x_2+b$

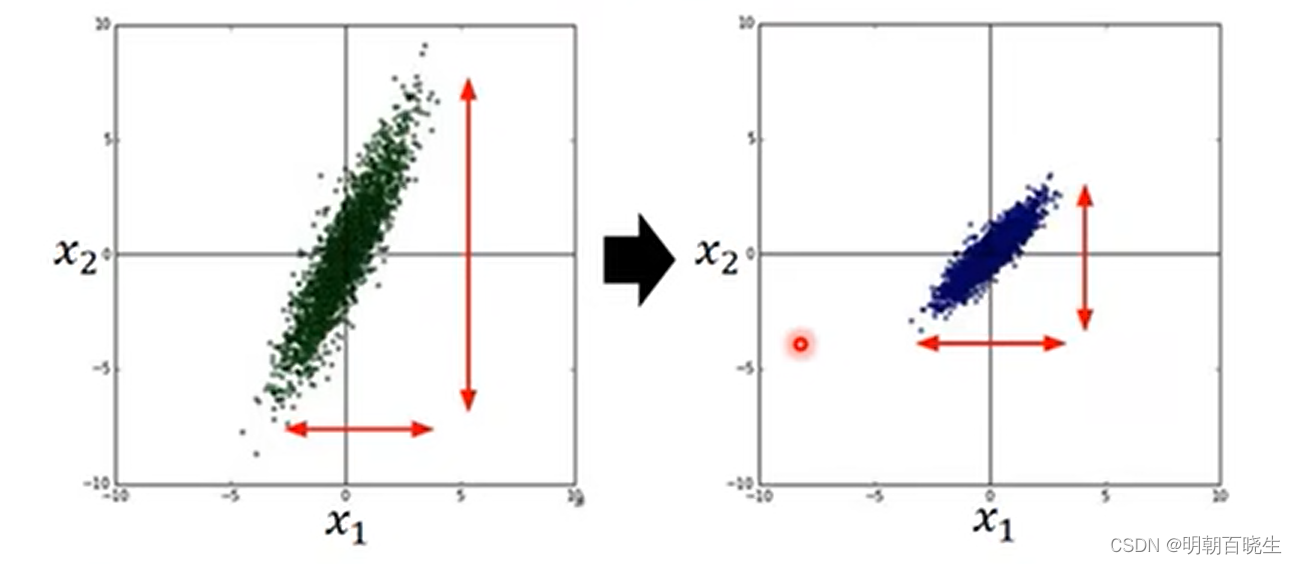
主要作用：

例子：

假设

$y=w_1x_1+w_2x_2+b$

$l=\frac{1}{2}(\hat{y}-y)^2$

则

$\bigtriangledown w_1=(y-\hat{y})x_1$

$\bigtriangledown w_2=(y-\hat{y})x_2$

如 $x_1,x_2$ 相差很大的时候，同样的loss,会导致不同维度

梯度变化相差非常大,当使用随机梯度下降时候，不同的出发点

收敛速度会相差很大。但是使用batchnormalization 方案后，

无论从哪个出发点出发,都不会影响收敛速度.

四梯度下降限制

4.1 任务说明：

根据前9小时的数据,预测下一个小时的PM2.5值

4.2 数据集

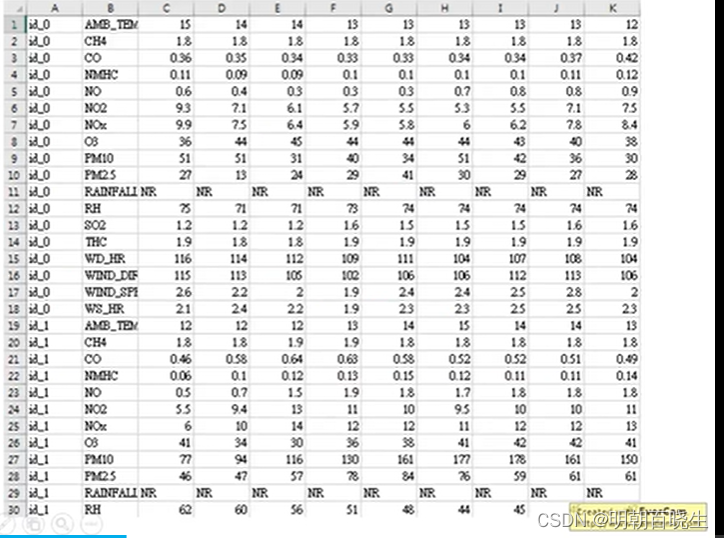
使用丰原站的观测记录，分成 train set 跟 test set，train set 是丰原站每个月的前 20 天所有资料。test set 则是从丰原站剩下的资料中取样出来。
train.csv: 每个月前 20 天的完整资料。
test.csv : 从剩下的资料当中取样出连续的 10 小时为一笔，前九小时的所有观测数据当作 feature，第十小时的 PM2.5 当作 answer。一共取出 240 笔不重複的 test data，请根据 feature 预测这 240 笔的 PM2.5。
Data 含有 18 项观测数据 AMB_TEMP, CH4, CO, NHMC, NO, NO2, NOx, O3, PM10, PM2.5, RAINFALL, RH, SO2, THC, WD_HR, WIND_DIREC, WIND_SPEED, WS_HR。

工程两个文件：

dataLoader.py

main.py


import pandas as pd
import numpy as np
import math


def get_testData(mean_x,std_x):
    #[4320 个数据，18个fetature 为一组，所有共有240个testData]
    print("\n mean_x",mean_x)
    testdata = pd.read_csv('data/test.csv',header=None, encoding = 'big5')
    
    test_data = testdata.iloc[:, 2:]
    test_data = test_data.copy()
    test_data[test_data == 'NR'] = 0
 
    test_data = test_data.to_numpy()
    #print("\n ---",test_data[0])
    test_x = np.empty([240, 18*9], dtype = float)
    for i in range(240):
        a = test_data[18 * i: 18* (i + 1), :].reshape(1, -1)
        #print("\n i ",i, a.shape)
        test_x[i, :] = test_data[18 * i: 18* (i + 1), :].reshape(1, -1)
      
    for i in range(len(test_x)):
        for j in range(len(test_x[0])):
            if std_x[j] != 0:
                test_x[i][j] = (test_x[i][j] - mean_x[j]) / std_x[j]
   
    test_x = np.concatenate((np.ones([240, 1]), test_x), axis = 1).astype(float)
    
    print("\n test_x",test_x.shape)
    return test_x
    

def load_data():
    
    data = pd.read_csv('data/train.csv', encoding='big5')
 
    
    #提取第三列后面的资料
    data = data.iloc[:,3:]
    data[data=='NR']=0
    raw_data = data.to_numpy() #[4320,24]
    #print(raw_data.shape)
    #print(data.head(18))
    return raw_data

def extract_traindata(month_data):
    '''
    用前9小时的18个特征预测 预测第10小时的PM2.5

    
    ----------
    month_data : TYPE
       key:   month
       item:  day1[24小时],data2[24小时]，...data20[24小时]
    Returns
    -------
    x : TYPE
        DESCRIPTION.
    y : TYPE
        DESCRIPTION.

    '''
    #每个月480小时(20天)，每9小时形成一个data,共有471data，所以训练集有12*471各数据
    #因为作业要求用前9小时,前9小时有18各feature
    x = np.empty([12*471,18*9],dtype=float)
    y = np.empty([12*471,1],dtype=float)
    
    for month in range(12):
        for day in range(20):
            for hour in range(24):
                
                if day ==19 and hour>14: 
                    continue
                else:
                    #每个小时的18项数据
                    data_start = day*24+hour
                    data_end = data_start+9
                    x[month*471+data_start,:]=month_data[month][:,data_start:data_end].reshape(1,-1)#前9小时
                    # pm标签值
                    y[month*471+data_start,0]=month_data[month][9,data_end] #第10个小时
    return x,y
                    
def  data_normalize(x):
    # 4.归一化
    mean_x = np.mean(x, axis = 0) #求列方向的均值
    std_x = np.std(x, axis = 0) #1列方向的方差
    print("\n shape ",x.shape)

    m,n =x.shape
    
 
    for i in range(m): #12 * 471
        for j in range(n): #18 * 9 
            if std_x[j] != 0:
                x[i][j] = (x[i][j] - mean_x[j]) / std_x[j]
    return x,mean_x,std_x


def train_load(x,y):
    x_train_set = x[: math.floor(len(x) * 0.8), :]
    y_train_set = y[: math.floor(len(y) * 0.8), :]
    x_validation = x[math.floor(len(x) * 0.8): , :]
    y_validation = y[math.floor(len(y) * 0.8): , :]
    print(x_train_set)
    (y_train_set)
    print(x_validation)
    print(y_validation)
    print(len(x_train_set))
    print(len(y_train_set))
    print(len(x_validation))
    print(len(y_validation))


def extract_features(raw_data):
    '''

    Parameters
    ----------
    raw_data : TYPE
        行:12个月，每月20天，每天18个特征。 [AMB_TEMP，CH4,CO,NMHC,NO,NO2,NOx,O3,PM10,PM2.5,RAINFALL,RH,SO2,THC,WD_HR,WIND_DIREC,WIND_SPEED,WS_HR]
        列：24小时 

    Returns
    -------
    month_data : TYPE
        12个月的词典
        比如针对AMB_TEMP 特征： 原来分成20行（每行24小时)， 现在放在一行: 20(天）*24(小时)

    '''

    
    month_data ={}
    for month in range(12):
        #
        sample = np.empty([18,480])    
        for day in range(20):
            sample[:, day * 24 : (day + 1) * 24] = raw_data[18 * (20 * month + day) : 18 * (20 * month + day + 1), :]
        month_data[month] = sample
    return month_data
    
def  load_trainData():
    
    #原始的数据集[ 12个月:每个月20天: 每天24小时，18个特征 ]
    raw_data = load_data()
    month_data  = extract_features(raw_data)
    x,y = extract_traindata(month_data)
    x,mean_x,std_x = data_normalize(x)
    
    return x,y,mean_x,std_x

# -*- coding: utf-8 -*-
"""
Created on Fri Dec  1 16:36:16 2023

@author: chengxf2
"""

# -*- coding: utf-8 -*-
"""
Created on Thu Nov 30 17:49:04 2023

@author: chengxf2
"""


import numpy as np
import csv
from  dataLoader import load_trainData
from  dataLoader import  get_testData

def predict(test_x):
    w = np.load('weight.npy')
    y = np.dot(test_x, w)
  
    with open('submit.csv', mode='w', newline='') as submit_file:
        csv_writer = csv.writer(submit_file)
        header = ['id', 'value']
        print(header)
        csv_writer.writerow(header)
        for i in range(240):
            row = ['id_' + str(i), y[i][0]]
            csv_writer.writerow(row)
            #print(row)
    submit_file.close()
    



def train(x,y):
    #w=[b,w]  
    #y = Xw
    dim = 1+18 * 9 #加上1个偏置
    w = np.zeros([dim, 1])
    x = np.concatenate((np.ones([12 * 471, 1]), x), axis = 1).astype(float)
    
    
    learning_rate = 1e-4
    iter_time = 1000
    adagrad = np.zeros([dim, 1])
    eps = 1e-6
    
    for t in range(iter_time):
        bias = np.dot(x, w) - y
        loss = np.sqrt(np.sum(np.power(bias, 2))/471/12)#rmse
        
        if(t%100==0):
            print("\n \n %d"%t,"\t loss: %6.3f"%loss)
        gradient = 2 * np.dot(x.transpose(), bias) #dim*1
        adagrad += gradient ** 2
        w = w - learning_rate * gradient / np.sqrt(adagrad + eps)
    np.save('weight.npy', w)
    
if __name__ == "__main__":
    x,y,mean_x,std_x = load_trainData()
    
    train(x,y)
    test_x =get_testData(mean_x,std_x)
    predict(test_x)

参考：

Hung-yi Lee

https://blog.csdn.net/Sinlair/article/details/127100363