💕"从前种种譬如昨日死;从后种种譬如今日生"💕
作者:Mylvzi
文章主要内容:数据结构之二叉树及面试题讲解
一.概念
1.树的定义
树是一种非线性的数据结构,是由n个结点组成的一种非线性集合;之所以叫做树,是因为他看起来像一颗倒挂的树,也就是根朝上,叶子朝下,一颗二叉树具有以下特征
- 有一个特殊节点--根节点 一颗二叉树有且仅有一个根节点
- 树是递归定义的
2.树与非树
如何判断一棵树是否是树呢?可以通过以下几个方式
- 除根节点外,其余结点有且仅有一个父节点
- 一棵树如果有n个结点,则一定有n-1条边
- 子树是不相交的
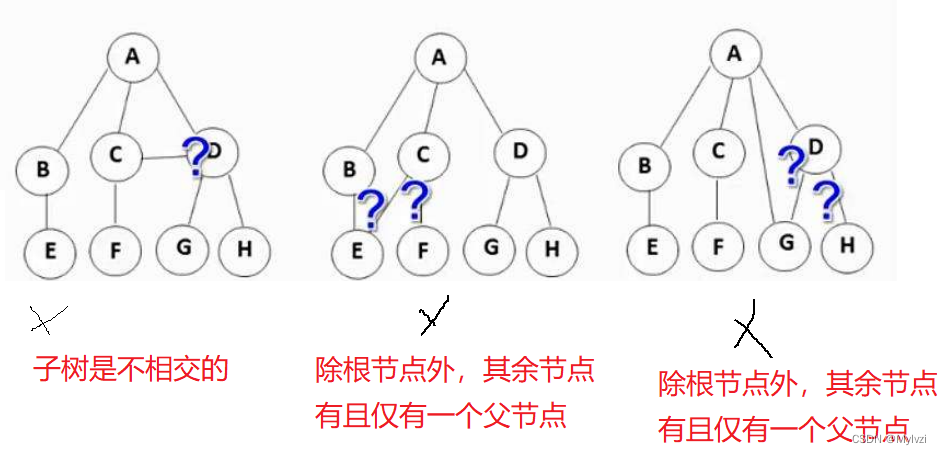
3.树的相关概念
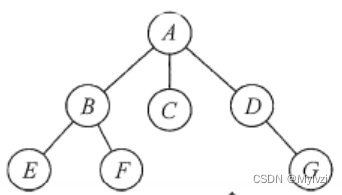
- 度:某个结点的子结点个数就叫做该节点的度 比如B结点的度就是2,因为其有两个子节点
- 树的度:指的是结点度的最大值 如图A结点的度是3,所以树的度就是3
- 叶子节点(终端节点):没有子节点的结点 比如E,F,G
- 祖先节点:所有节点的父节点 就是根节点 本图中A结点时祖先节点
- 父节点:结点的前驱结点就是父节点,也叫做双亲结点 B是E,F的父节点
- 孩子节点:与父结点相对
- 树的高度:树的层次的最大值就是树的高度 如图层次是三,所以树的高度就是3
- 树的以下概念只需了解,在看书时只要知道是什么意思即可:
- 非终端结点或分支结点:度不为0的结点;
- 兄弟结点:具有相同父结点的结点互称为兄弟结点;
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟;
- 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
4.树的表示形式(了解)
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法, 孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
class Node {
int value; // 树中存储的数据
Node firstChild; // 第一个孩子引用
Node nextBrother; // 下一个兄弟引用
}二. 二叉树(重点)
1.概念
二叉树是树形结构的一种,二叉树就是度<= 2的的树

二叉树是由以下几种情况组成

2.两种特殊的二叉树
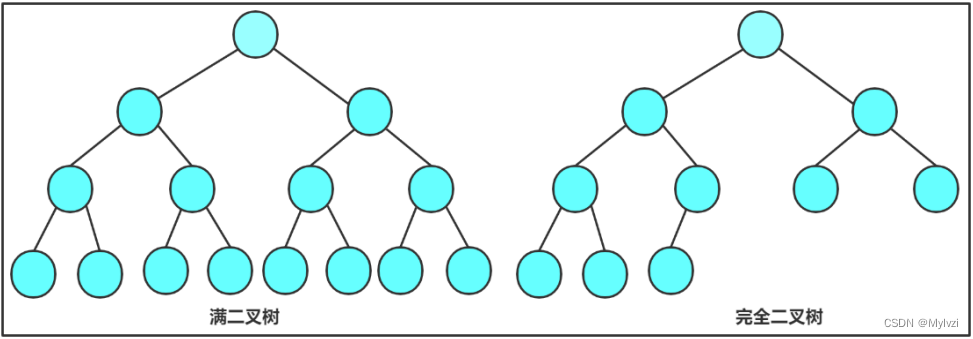
- 满二叉树: 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵 二叉树的层数为K,且结点总数是 2^k - 1,则它就是满二叉树。
- 完全二叉树: 完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n 个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完 全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。
- 完全二叉树就是从上到下,从左到右依次存放结点的树
3.二叉树的性质(重点 )
- 若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有(2^i - 1) (i>0)个结点
- 若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是(2^k - 1) (k>=0)推导:等比数列的求和公式推导而成
- 具有n个结点的完全二叉树的深度k 为 Log(n+1)向 上取整
- 对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1 也就是叶子节点的个数一定比度为2的结点的个数多一

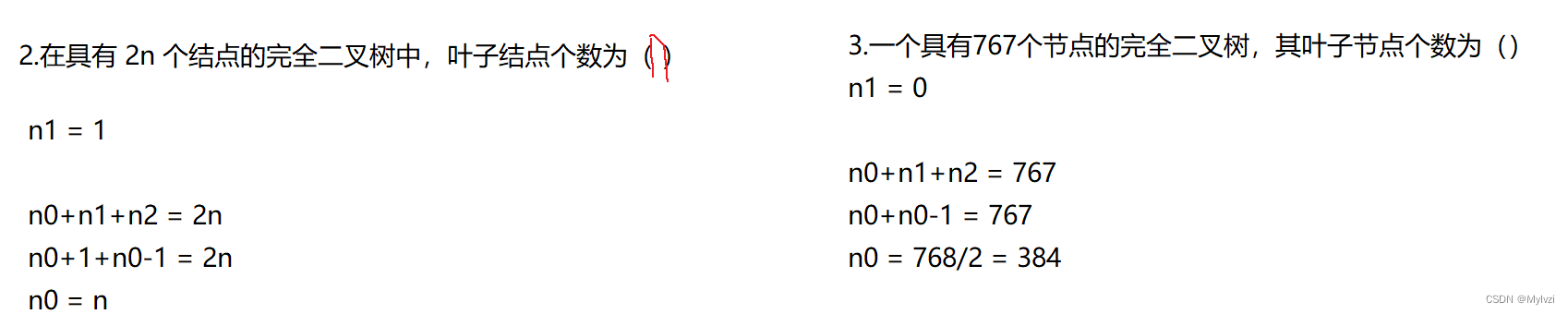
这个性质经常作为考试题目,会结合结点数目的奇偶性以及完全二叉树来出题

如果结点数是2N,则n1的个数一定是1
如果结点数是2N+1,则n1的个数一定是0
4.二叉树的存储
二叉树的存储结构分为:顺序存储和链式存储
顺序存储的底层其实是"堆"这种数据结构的实现,也就是二叉搜索树
我们以链式的存储结构进行讲解
二叉树的链式存储结构是通过一个一个结点实现的,最常用的表示方法是左右孩子表示法,即每个节点存储左右孩子结点
定义结点内部类
static class TreeNode {
public int val;
public TreeNode lChild;// 左孩子
public TreeNode rChild;// 右孩子
public TreeNode(char val) {
this.val = val;
}
}手动插入结点
public TreeNode create() {
TreeNode A = new TreeNode('A');
TreeNode B = new TreeNode('B');
TreeNode C = new TreeNode('C');
TreeNode D = new TreeNode('D');
TreeNode E = new TreeNode('E');
TreeNode F = new TreeNode('F');
TreeNode G = new TreeNode('G');
TreeNode H = new TreeNode('H');
A.lChild = B;
A.rChild = C;
B.lChild = D;
B.rChild = E;
C.lChild = F;
C.rChild = G;
E.rChild = H;
return A;
}2.二叉树的遍历
遍历是二叉树的一个很重要的操作,二叉树作为一种存储数据的结构,在我们获取数据的时候需要遍历整棵二叉树,直到拿到我们所需要的数据,不同的遍历方式也会带来不同的效率,二叉树常见的遍历方式有:
- 前序遍历preOrder 根左右
- 中序遍历inOrder 左根右
- 后序遍历postOrder 左右根
- 层序遍历levelOrder 从上至下从左至右依次遍历每一个结点
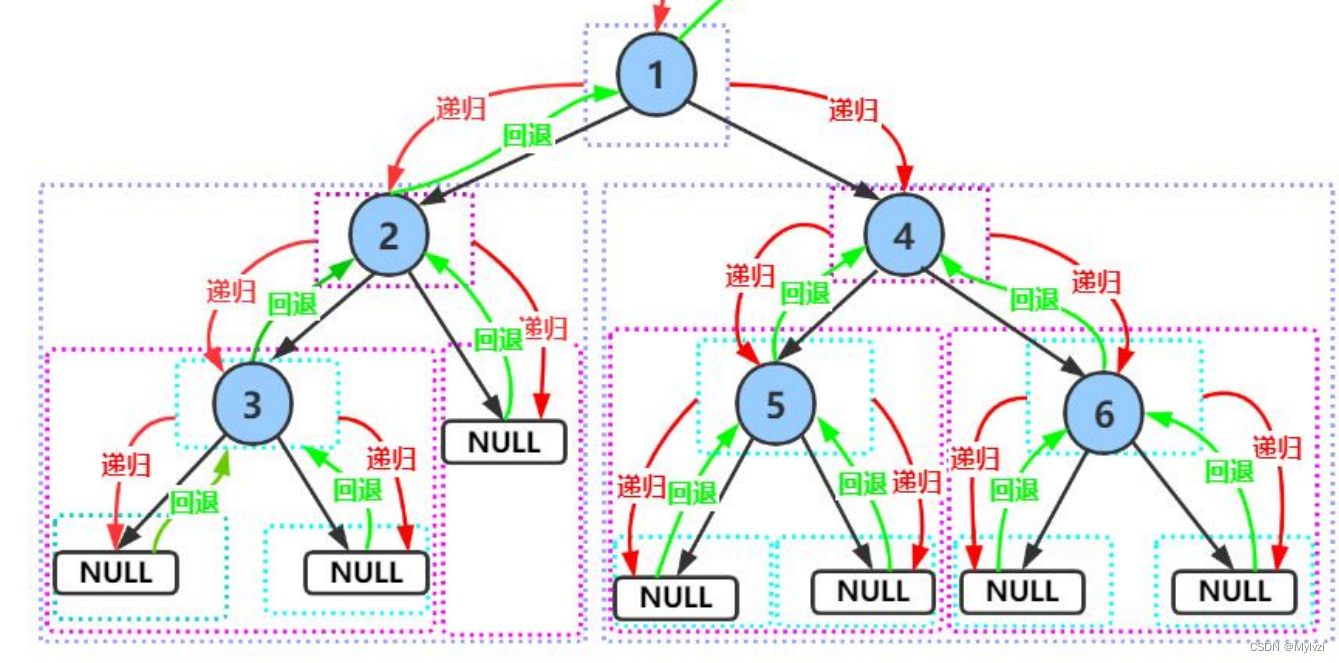
遍历操作最核心的思路就是"子问题思路"和递归的思想,下面进行遍历的代码实现
把整棵二叉树想象为只有一个根节点和两个孩子节点的树,很多二叉树的问题就容易解决
要谨记,二叉树有两种,空树和非空树,任何情况下都不要忘记空树的情况
1,前序遍历
// 前序
public void preOrder(TreeNode root) {
// 空树直接返回
if(root == null) return;
System.out.print(root.val+" ");
// 打印完根节点再去访问左孩子和右孩子
preOrder(root.lChild);
preOrder(root.rChild);
}
力扣题目
https://leetcode.cn/problems/binary-tree-preorder-traversal/submissions/
代码实现
public List<Integer> preorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
// 空树直接返回
if(root == null) return list;
list.add(root.val);
// 遍历左子树
List<Integer> leftTree = preorderTraversal(root.left);
list.addAll(leftTree);
// 遍历右子树
List<Integer> rightTree = preorderTraversal(root.right);
list.addAll(rightTree);
return list;
}2.中序遍历
// 中序
public void inOrder(TreeNode root) {
// 空树 直接返回
if(root == null) return;
inOrder(root.lChild);
System.out.print(root.val+" ");
inOrder(root.rChild);
}https://leetcode.cn/problems/binary-tree-inorder-traversal/submissions/
代码实现
public List<Integer> inorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
// 空树 直接返回
if(root == null) return list;
// 遍历左子树
List<Integer> leftTree = inorderTraversal(root.left);
list.addAll(leftTree);
list.add(root.val);
// 遍历右子树
List<Integer> rightTree = inorderTraversal(root.right);
list.addAll(rightTree);
return list;
}3,后序遍历
public void postOrder(TreeNode root) {
// 空树 直接返回
if(root == null) return;
postOrder(root.lChild);
postOrder(root.rChild);
System.out.print(root.val+" ");
}https://leetcode.cn/problems/binary-tree-preorder-traversal/submissions/
代码实现
public List<Integer> postorderTraversal(TreeNode root) {
List<Integer> list = new ArrayList<>();
if(root == null) return list;
// 遍历左子树
List<Integer> leftTree = postorderTraversal(root.left);
list.addAll(leftTree);
// 遍历右子树
List<Integer> rightTree = postorderTraversal(root.right);
list.addAll(rightTree);
list.add(root.val);
return list;
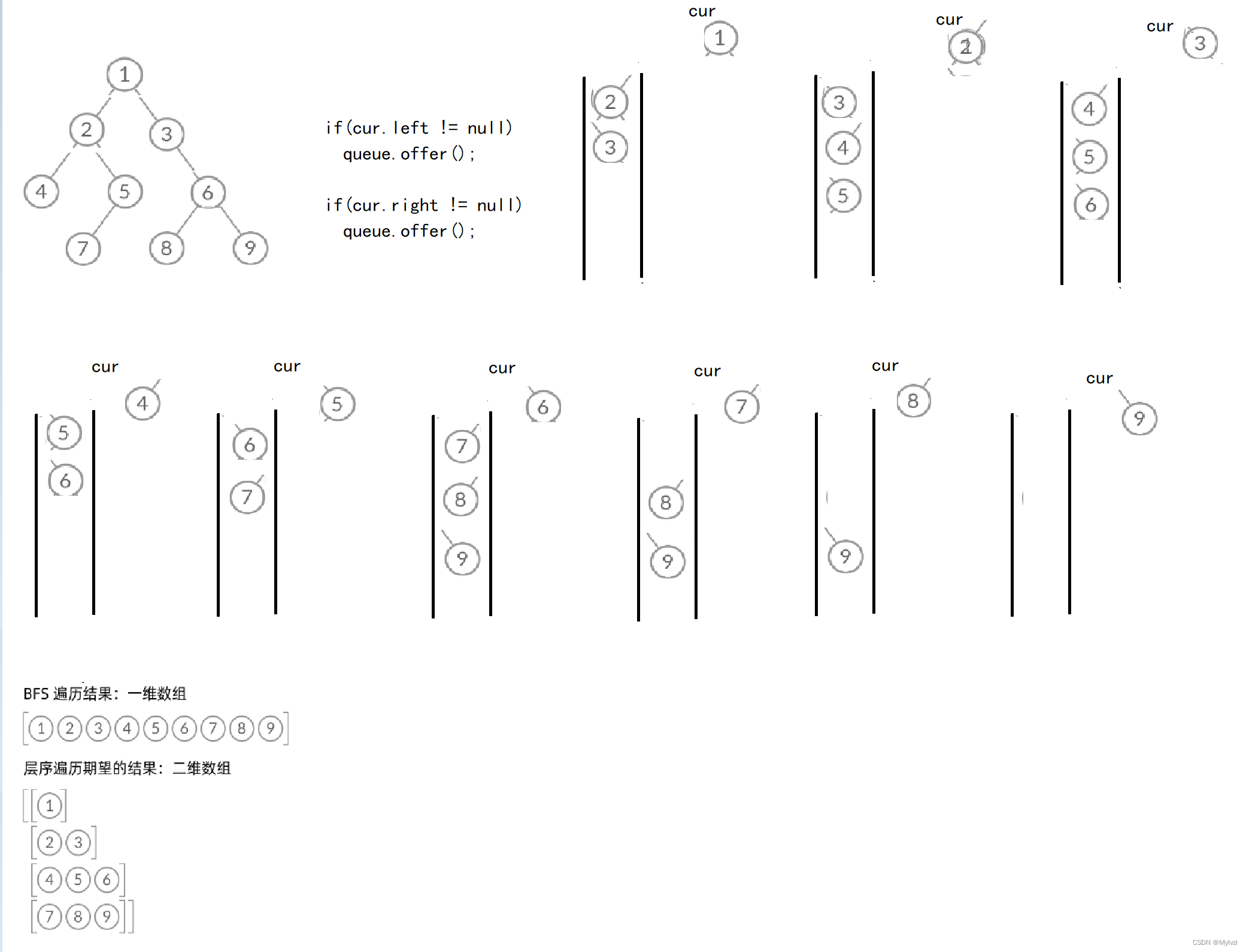
}4.层序遍历
使用队列来模拟实现(自己画图想一下,很简单)
/**
* 层序遍历 一层一层的遍历 打印
* 先遇到 先打印 fifo 先进先出 使用队列存储遍历的结点
* @param root
*/
// 层序遍历
public void levelOrder(TreeNode root) {
if(root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
TreeNode cur = queue.poll();
System.out.print(cur.val+" ");
if (cur.lChild != null) {
queue.offer(cur.lChild);
}
if (cur.rChild != null) {
queue.offer(cur.rChild);
}
}
}https://leetcode.cn/problems/binary-tree-level-order-traversal/submissions/
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> ret = new ArrayList<>();
if(root == null) return ret;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while(!queue.isEmpty()) {
List<Integer> tmpList = new ArrayList<>();
// 记录当前队列中的结点个数 决定了当前层的tmpList存储的结点个数 也方便添加后序的孩子节点
int size = queue.size();
while(size > 0) {
TreeNode cur = queue.poll();
if(cur.left != null) queue.offer(cur.left);
if(cur.right != null) queue.offer(cur.right);
tmpList.add(cur.val);
size--;
}
ret.add(tmpList);
}
return ret;
}3.二叉树的基本操作
5.求结点个数
最基本的思路就是定义一个计数器,遍历每一个结点,遍历的方法可以是前序,中序,后序,层序,下面实现两种:递归实现和子问题思路
注:这里的递归实现采用了前序遍历的方式
/**
* 求size 遍历每一个结点 设置一个计数器
*/
public int size = 0;
public int getSize(TreeNode root) {
// 空树 直接返回 结点数为1
if(root == null) return 0;
size++;
getSize(root.lChild);
getSize(root.rChild);
return size;
}
// 子问题思路:结点的个数 == 左子树的节点个数+右子树的结点个数+根节点
public int getSize2(TreeNode root) {
if(root == null) return 0;
return getSize2(root.lChild) +
getSize2(root.rChild) + 1;
}6.求叶子节点的个数
叶子节点即左右孩子都为空的结点,要求叶子节点的个数,需要遍历寻找;
/**
* 求叶子节点的个数
* 1.遍历实现 满足左右节点都为空 ++
* 2.子问题思路:root叶子节点的个数 == 左子树叶子节点的个数+右子树叶子节点的个数
*/
public int leafSize = 0;
public int getLeafSize(TreeNode root) {
// 递归结束条件 这其实是二叉树的一种情况
// 二叉树有两类 空树 和非空树
// 空树 没有叶子结点 返回0
if(root == null) return 0;
if (root.lChild == null && root.rChild == null) {
leafSize++;
}
getLeafSize(root.lChild);
getLeafSize(root.rChild);
return leafSize;
}
public int getLeafSize2(TreeNode root) {
// 子问题思路
// root叶子节点的个数 == 左子树叶子节点的个数+右子树叶子节点的个数
if(root == null) return 0;
if(root.lChild == null && root.rChild == null) return 1;
return getLeafSize2(root.lChild) + getLeafSize2(root.rChild);
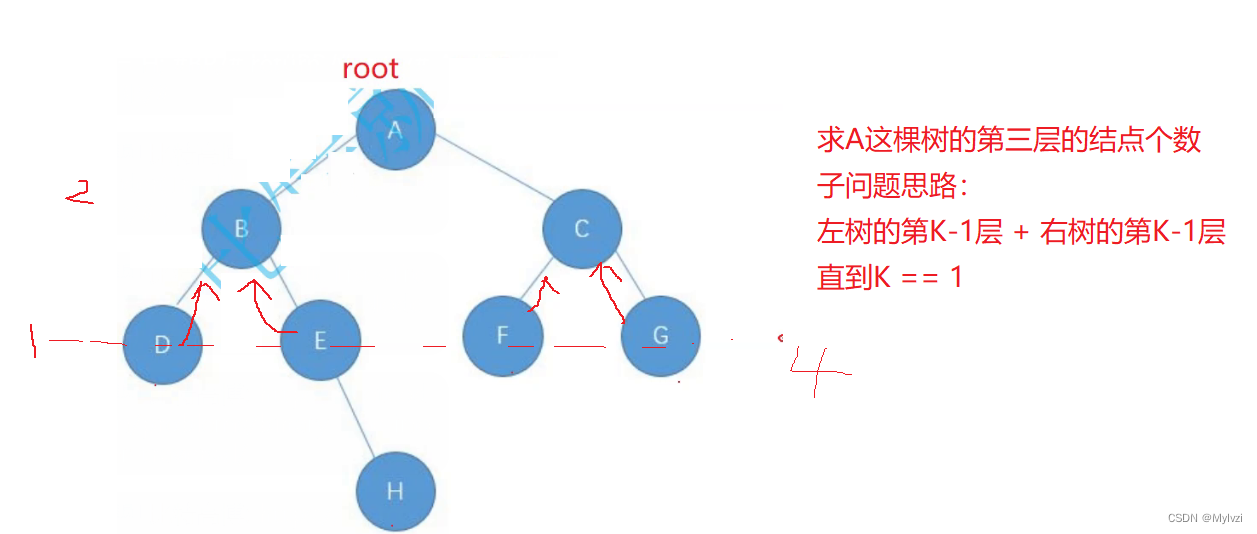
}7.求第k层的结点个数
转化为子问题思路
/**
* 获取第k层结点的个数
* 子问题思路:等价于左树第k-1层和右树第k-1层结点的个数
* 一直走到第k层
* @param root
* @param k
* @return
*/
public int getKLevelNodeConut(TreeNode root,int k) {
if(root == null) return 0;
// 等于1 证明走到了第k层 现在就是第k层的某一个节点
if(k == 1) return 1;
return getKLevelNodeConut(root.lChild,k-1) +
getKLevelNodeConut(root.rChild,k-1);
}8.求树的高度
子问题思路:树的高度 = 左树和右树高度的最大值+1
// 这种方法可以通过 递归只计算了一次
public int getHeight(TreeNode root) {
// 想好递归条件 最后一定是走到null结点 其高度为0 往回归
if(root == null) return 0;
int leftHeight = getHeight(root.lChild);
int rightHeight = getHeight(root.rChild);
return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;
}9.判断是否包含某节点
先判断根节点 再去遍历左子树 左子树包含 直接返回 不包含 遍历右子树
/**
* 判断是否含有某个值的结点
*/
public boolean find(TreeNode root,char val) {
// 为空 直接返回
if(root == null) return false;
if(root.val == val) return true;
// 遍历左子树 如果找到,则flg1为true 直接返回即可 不需要再去遍历右子树
boolean flg1 = find(root.lChild,val);
if(flg1) return true;
// 遍历右子树
boolean flg2 = find(root.rChild,val);
if(flg2) return true;
return false;
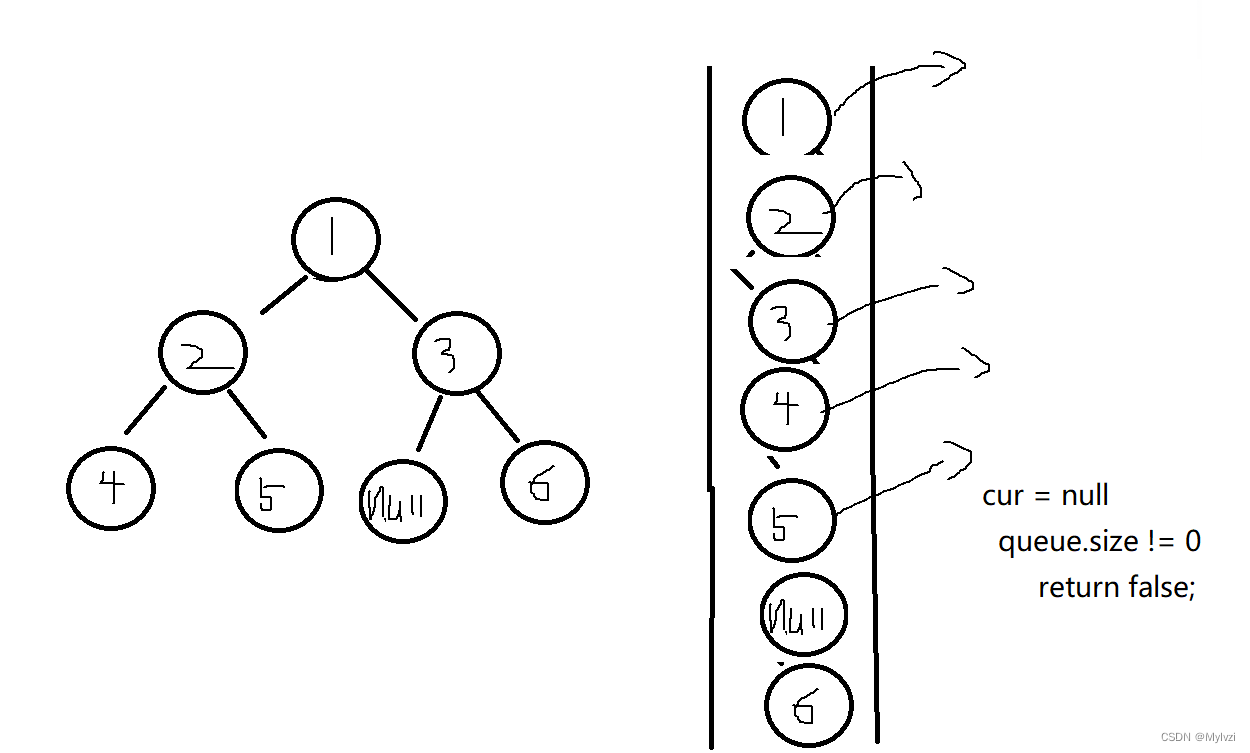
}10.判断是否是完全二叉树
利用层序遍历的思路,把当前结点的所有孩子结点都加入(如果孩子节点是null也会被插入),当遇到null时,如果是完全二叉树,则此结点一定是最后一个节点,即queue.size == 0,如果不是完全二叉树,则queue.size != 0
/**
* 判断是否是完全二叉树
* 层序遍历的思路 把所有结点的左右孩子节点都存入到queue中 如果遇到null 去判断是否还存在元素
* 存在 -- 不是完全二叉树
* @param root
* @return
*/
public boolean iscompleteTree(TreeNode root) {
if(root == null) return true;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode cur = queue.poll();
// 如果queue中存储的是null 它会被存储到queue中 但却不算有效数据个数
if (cur == null) {
if(queue.size() != 0) {
return false;
}
}
queue.offer(cur.lChild);
queue.offer(cur.rChild);
}
return true;
}三.二叉树的相关OJ题目
二叉树作为面试中常考的题目有一定的难度(且难度不小),需要认真去练习,总结
1.判断两棵树是否相同
https://leetcode.cn/problems/same-tree/submissions/
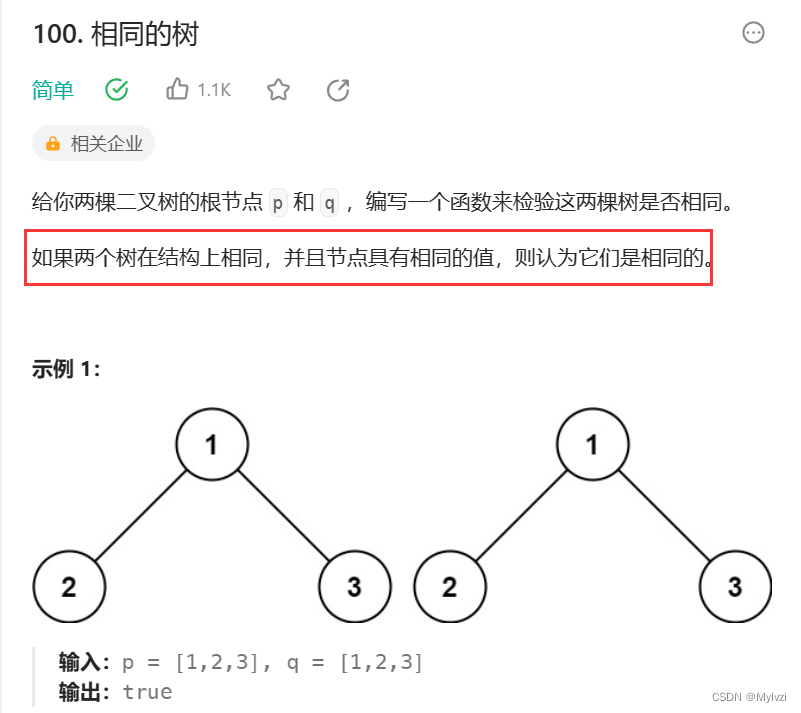
思路分析:
这题可以采用子问题思路 先分析判断的思路,先判断结构上是否一致,如果一致,再去判断值是否相同
- 如果一个为空,一个不为空,结构上不同 返回false
- 如果两个都为空 返回true
- 如果结构上完全相同,去判断值是否相同
代码实现
// 先判断当前所在根是否相同 不同 判断左结点 再判断右节点
// 不同 值不同 一个为空,一个不为空
// 相同 值相同 或者两个都为空
// 一个为空,一个不为空
if(p != null && q == null || p == null && q != null) return false;
// 两个都为空 认为相等
if(p == null && q == null) return true;
// 值不同 走到这里说明两个引用都不为空 只需判断值是否相同即可
if(p.val != q.val) return false;
return isSameTree(p.left,q.left) &&
isSameTree(p.right,q.right);2.另一棵树的子树
https://leetcode.cn/problems/subtree-of-another-tree/description/

思路分析
- 先判断root是否是null,为空直接返回false
- 判断当前根节点是否和subRoot是否是相同的树
- 再去递归遍历root的左树和右数是否和subRoot是相同的树
代码实现
class Solution {
private boolean isSameTree(TreeNode p,TreeNode q) {
if(p == null && q != null || p != null && q == null) return false;
if(p == null && q == null) return true;
if(p.val != q.val) return false;
return isSameTree(p.left,q.left) &&
isSameTree(p.right,q.right);
}
public boolean isSubtree(TreeNode root, TreeNode subRoot) {
if(root == null ) return false;
// 判断当前节点是否满足条件
if(isSameTree(root,subRoot)) return true;
// 递归遍历左树和右树
if(isSubtree(root.left,subRoot)) return true;
if(isSubtree(root.right,subRoot)) return true;
// 走到这里 说明以上情况都不满足 直接返回false;
return false;
}
}3.翻转二叉树

思路分析
还是利用子问题思路,交换root的左右子树,再去更新root,继续交换左右子树
https://leetcode.cn/problems/invert-binary-tree/submissions/
代码实现
public TreeNode invertTree(TreeNode root) {
if(root == null) return root;
// 交换
TreeNode tmp = root.left;
root.left = root.right;
root.right = tmp;
// 交换根节点的左子树和右子树
invertTree(root.left);
invertTree(root.right);
return root;
}4.判断平衡二叉树
https://leetcode.cn/problems/balanced-binary-tree/submissions/
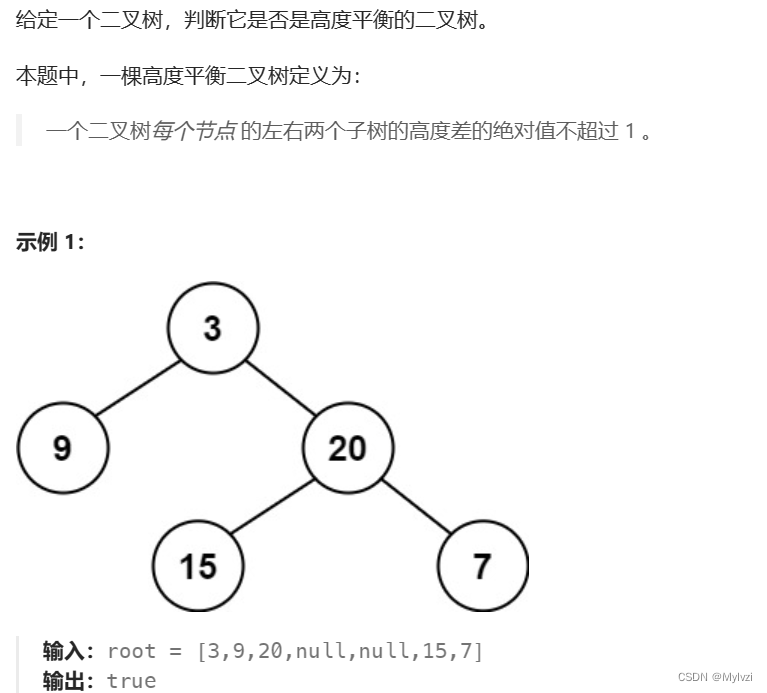
1.遍历每一个节点 判断其左右子树是否平衡 只要求出当前结点左右子树的高度即可 同时还要保证其余节点也平衡
// 求树的高度
private int getHeight(TreeNode root) {
if(root == null) return 0;
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
return leftHeight > rightHeight ? leftHeight+1 : rightHeight+1;
}
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
// 高度平衡的条件 每颗结点都要高度平衡 即每颗结点的左右子树的高度差都要<=1
return Math.abs(leftHeight-rightHeight) <= 1 &&
isBalanced(root.left) &&
isBalanced(root.right);
}第一种方法时间复杂度达到了0(N^2),究其原因,在于在计算高度的时候发生了重复计算,在你求完root当前的高度之后还需要再去判断其左右子树是否平衡,判断的时候还需要再去求一遍高度,导致时间复杂度过高,我们发现,在求第一次高度时,整个求高度的过程中已经发现了不平衡的现象,我们可以在返回高度的过程中就去判断是否是平衡的
2.第二种思路
// 求树的高度
private int getHeight(TreeNode root) {
if(root == null) return 0;
int leftHeight = getHeight(root.left);
int rightHeight = getHeight(root.right);
// 返回正常高度的条件
if(leftHeight >= 0 && rightHeight >= 0 && Math.abs(leftHeight-rightHeight) <= 1) {
return Math.max(leftHeight,rightHeight)+1;
}else {
return -1;
}
}
public boolean isBalanced(TreeNode root) {
if(root == null) return true;
return getHeight(root) >= 0;
}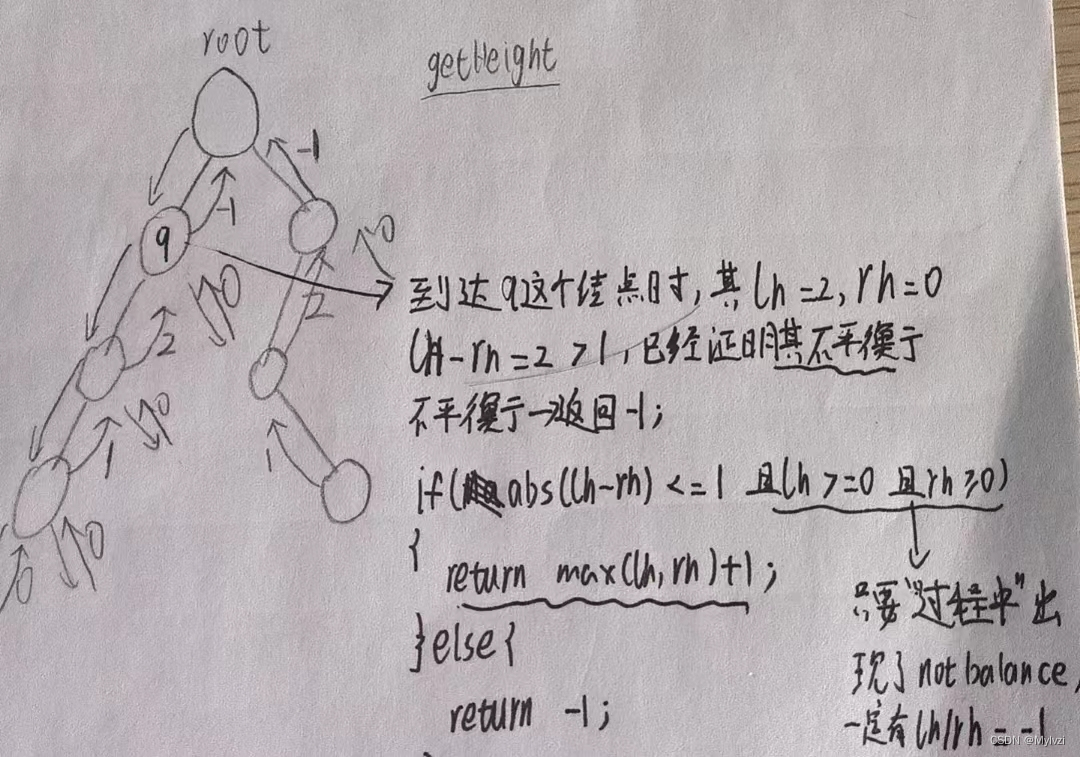
正常返回高度的条件是
- 左树高度和右树高度的绝对值之差 <= 1
- 左子树的高度符合条件 即左子树的高度不是-1
- 右子树的高度符合条件 即右子树的高度不是-1
这道题曾经是字节面试出的一道题,第一种思路很容易想到,即通过求当前结点的左右子树的高度的绝对值之差来判断是否符合条件,同时还要满足当前结点的左子树和右子树也符合条件(这一点也容易忽视),但这种思路存在着重复计算的问题 ,时间复杂度过高;
重复计算的是高度,那能不能在一次求高度的过程中就判断是否符合条件?答案是可以的,就是提供的第二种思路
这种在过程中判断是否符合条件从而减少计算量的思路经常出现,也不容易实现,可以好好学习,总结一下
5.二叉树的遍历
https://www.nowcoder.com/practice/4b91205483694f449f94c179883c1fef?tpId=60&&tqId=29483&rp=1&ru=/activity/oj&qru=/ta/tsing-kaoyan/question-ranking
思路分析:
本题是根据前序遍历的方式去创建二叉树,本质上还是利用递归的方式去创建树
先创建当前的根节点,再去创建结点的左树,最后创建结点的右树
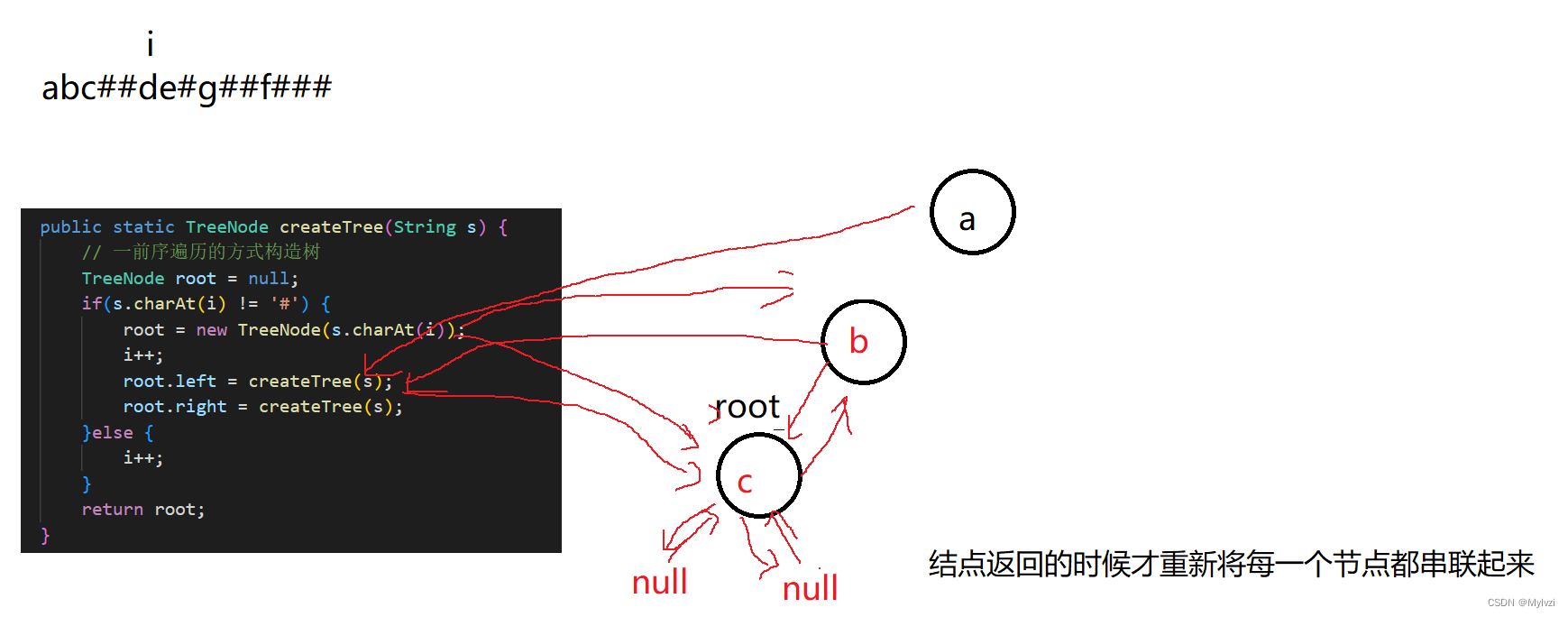
代码实现
import java.util.Scanner;
// 结点的信息需要自行创建
class TreeNode {
char val;
TreeNode left;
TreeNode right;
public TreeNode() {};
public TreeNode(char val) {
this.val = val;
};
}
// 注意类名必须为 Main, 不要有任何 package xxx 信息
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
// 注意 hasNext 和 hasNextLine 的区别
while (in.hasNextLine()) { // 注意 while 处理多个 case
String s = in.nextLine();
// 获取创建树的根节点
TreeNode root = createTree(s);
// 中序遍历
inOrder(root);
}
}
public static int i = 0;
// 根据前序遍历的结果创建一棵树
public static TreeNode createTree(String s) {
TreeNode root = null;
if(s.charAt(i) != '#') {
// 不是#号,证明就是一个结点 实例化一个结点 i++ 再去分别创建该节点的左树,右树
root = new TreeNode(s.charAt(i));
i++;
root.left = createTree(s);
root.right = createTree(s);
}else {// 是# 直接i++
i++;
}
// 递归到最后要把节点之间联系起来 所以返回root
return root;
}
// 中序遍历
public static void inOrder(TreeNode root) {
if(root == null) return;
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
}6.前序+中序构造二叉树
https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal/

代码实现
//**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return buildChildTree(preorder,inorder,0,inorder.length-1);
}
// 应该将pi设置为成员变量 否则在递归回退的过程中会重新返回值
public int pi;
public TreeNode buildChildTree(int[] preorder,int[] inorder,int beginIndex,int endIndex) {
// 1.没有左树 或者没有右树
if(beginIndex > endIndex) {
return null;
}
// 2.创建根节点
TreeNode root = new TreeNode(preorder[pi]);
// 3.在中序遍历中找到根节点
int rootIndex = find(inorder,beginIndex,endIndex,preorder[pi]);
if(rootIndex == -1) return null;
pi++;
// 创建左子树
root.left = buildChildTree(preorder,inorder,beginIndex,rootIndex-1);
// 创建右子树
root.right = buildChildTree(preorder,inorder,rootIndex+1,endIndex);
return root;
}
private int find(int[] inorder,int beginIndex,int endIndex,int key) {
for(int i = beginIndex; i <= endIndex; i++) {
if(inorder[i] == key) {
return i;
}
}
// 没找到 返回-1
return -1;
}
}7.后序+中序构造二叉树
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int pi;
public TreeNode buildTree(int[] inorder,int[] postorder) {
pi = postorder.length-1;
return buildChildTree(postorder,inorder,0,inorder.length-1);
}
public TreeNode buildChildTree(int[] postorder,int[] inorder,int beginIndex,int endIndex) {
if(beginIndex > endIndex) {
return null;
}
TreeNode root = new TreeNode(postorder[pi]);
int rootIndex = find(inorder,beginIndex,endIndex,postorder[pi]);
if(rootIndex == -1) return null;
pi--;
// 创建右子树
root.right = buildChildTree(postorder,inorder,rootIndex+1,endIndex);
// 创建左子树
root.left = buildChildTree(postorder,inorder,beginIndex,rootIndex-1);
return root;
}
private int find(int[] inorder,int beginIndex,int endIndex,int key) {
for(int i = beginIndex; i <= endIndex; i++) {
if(inorder[i] == key) {
return i;
}
}
// 没找到 返回-1
return -1;
}
}总结:
前序/后序+中序都能构造出一棵二叉树,如果是前序+后序无法得到
8.最近的公共祖先
http://leetcode.cn/problems/lowest-common-ancestor-of-a-binary-tree/


/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) return null;
Stack<TreeNode> stack1 = new Stack<>();
Stack<TreeNode> stack2 = new Stack<>();
getPath(root, p, stack1);
getPath(root, q, stack2);
int sizeP = stack1.size();
int sizeQ = stack2.size();
if (sizeP > sizeQ) {
int size = sizeP - sizeQ;
while (size != 0) {
stack1.pop();
size--;
}
} else {
int size = sizeQ - sizeP;
while (size != 0) {
stack2.pop();
size--;
}
}
// 此时两个栈的长度一致
while(!stack1.peek().equals(stack2.peek())) {
stack1.pop();
stack2.pop();
}
return stack1.peek();
}
/**
* 难点在于如何获得p,q路径上的所有节点
* 利用栈存放通过前序遍历遇到的每一个节点 判断结点的左右子树是否包含要寻找的结点
*/
private boolean getPath(TreeNode root, TreeNode node, Stack<TreeNode> stack) {
if(root == null || node == null) return false;
stack.push(root);
if(root == node) return true;
boolean flg1 = getPath(root.left,node,stack);
if(flg1) {
return true;
}
boolean flg2 = getPath(root.right,node,stack);
if (flg2) {
return true;
}
stack.pop();
return false;
}
}
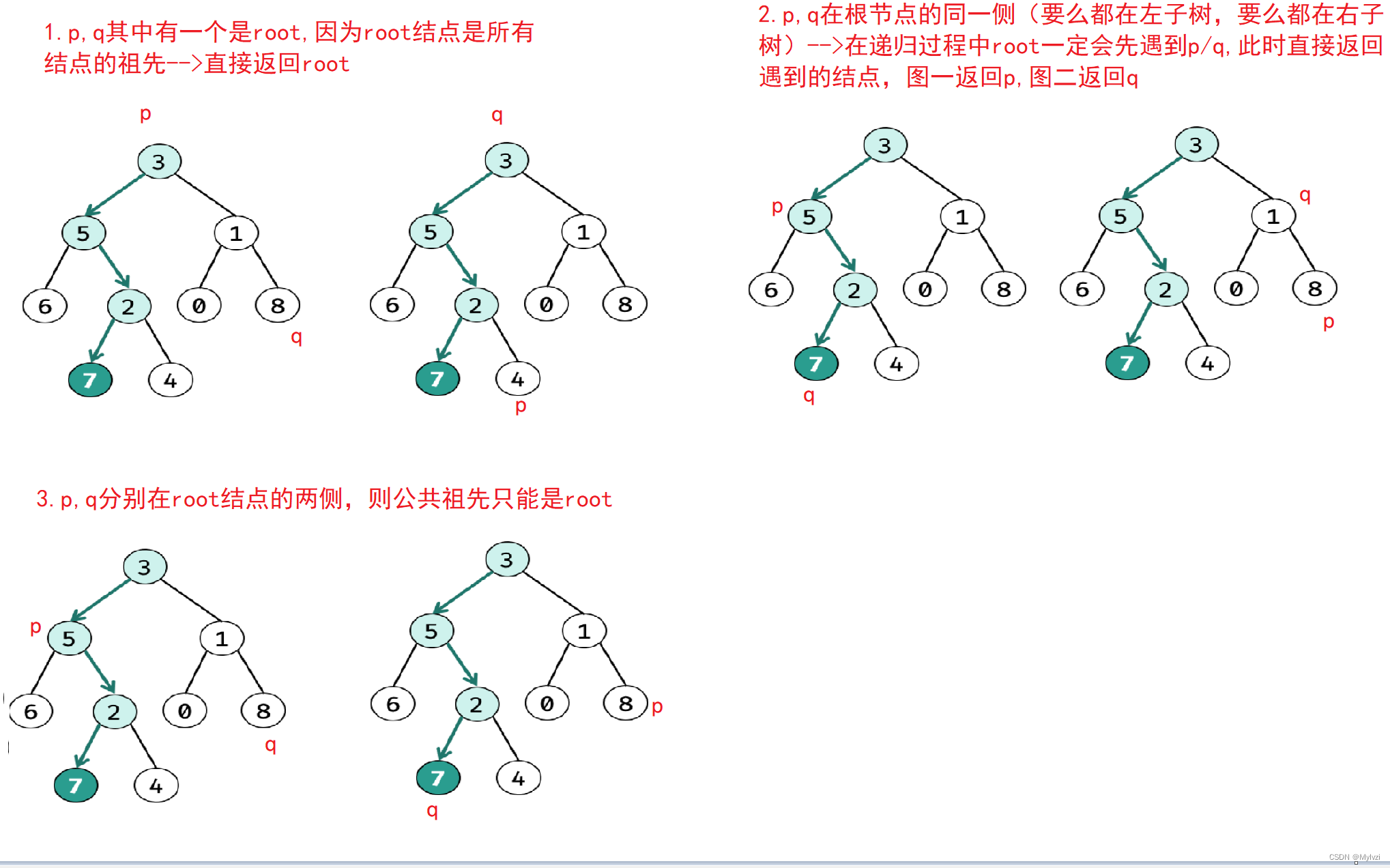
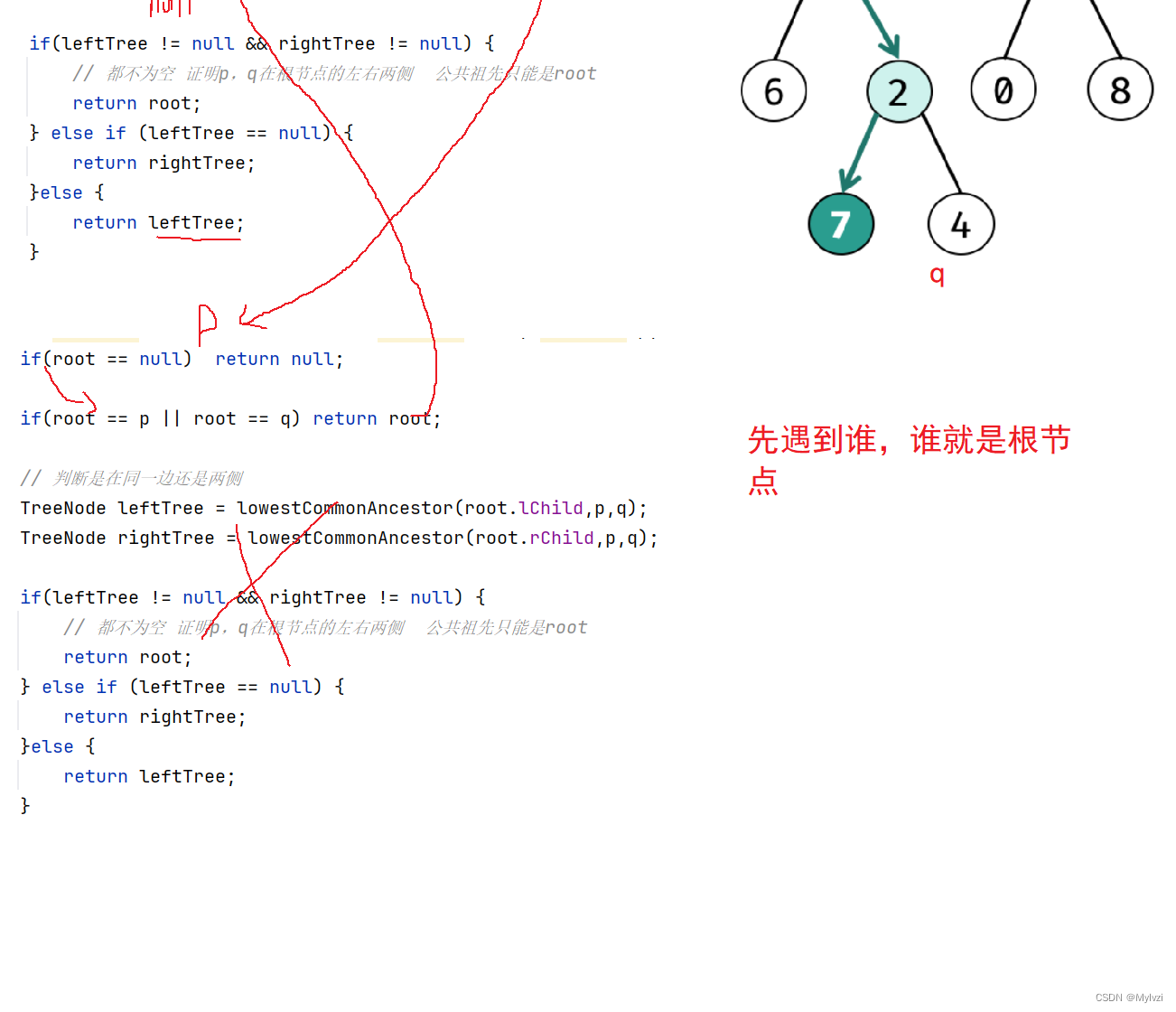
/**
* 找最近的公共祖先 三种情况
* @param root
* @param p
* @param q
* @return
*/
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root == null) return null;
if(root == p || root == q) return root;
// 判断是在同一边还是两侧
TreeNode leftTree = lowestCommonAncestor(root.lChild,p,q);
TreeNode rightTree = lowestCommonAncestor(root.rChild,p,q);
if(leftTree != null && rightTree != null) {
// 都不为空 证明p,q在根节点的左右两侧 公共祖先只能是root
return root;
} else if (leftTree != null) {
return leftTree;
}else {
return rightTree;
}
}