基本介绍
索引是帮助MySQL高效获取数据的数据结构,主要是用来提高数据检索的效率,降低数据库的IO成本,同时通过索引列对数据进行排序,降低数据排序的成本,也能降低了CPU的消耗。
通俗来说, 索引就相当于一本书的目录, 可以根据页码快速查找到指定的内容, 目的就是加快数据库的查询速度,但这也就意味着书中如果要增加一个章节,修改目录是比较麻烦的,使用索引适用于经常查询很少修改的业务
在 MySQL 中,通常有以下两种方式访问数据库表的行数据:
1) 顺序访问
- 顺序访问是在表中实行全表扫描,从头到尾逐行遍历,直到在无序的行数据中找到符合条件的目标数据。
- 顺序访问实现比较简单,但是当表中有大量数据的时候,效率非常低下。例如,在几千万条数据中查找少量的数据时,使用顺序访问方式将会遍历所有的数据,花费大量的时间,显然会影响数据库的处理性能。
2) 索引访问
- 索引访问是通过遍历索引来直接访问表中记录行的方式。
- 使用这种方式的前提是对表建立一个索引,在列上创建了索引之后,查找数据时可以直接根据该列上的索引找到对应记录行的位置,从而快捷地查找到数据。索引存储了指定列数据值的指针,根据指定的排序顺序对这些指针排序。
注意: 建立索引后, 查询速度不一定会变快,例如, 你在teacher表中建立了关于
id的索引, 如果你按照name查询, 那么查询速度也不会变快,查询得用到你建立的索引
优缺点
优点:
- 创建索引可以大幅提高系统性能,帮助用户提高查询的速度;
- 可以加速表与表之间的链接;
- 降低查询中分组和排序的时间。
缺点:
- 索引的存储需要占用磁盘空间;
- 当数据的量非常巨大时,索引的创建和维护所耗费的时间也是相当大的;
- 当每次执行create、update、delete操作时,索引也需要动态维护,降低了数据的维护速度。
空间换时间
索引的底层数据结构
B树
B树树就是B-树,它是一种平衡的多叉树,不是B减树,而是B杠树,中文通常称为B树,英语称为B-tree。
人们可能会以为B-树是一种树,而B树又是一种一种树。而事实上是,B-tree就是指的B树。
B 树的结构如下图所示:
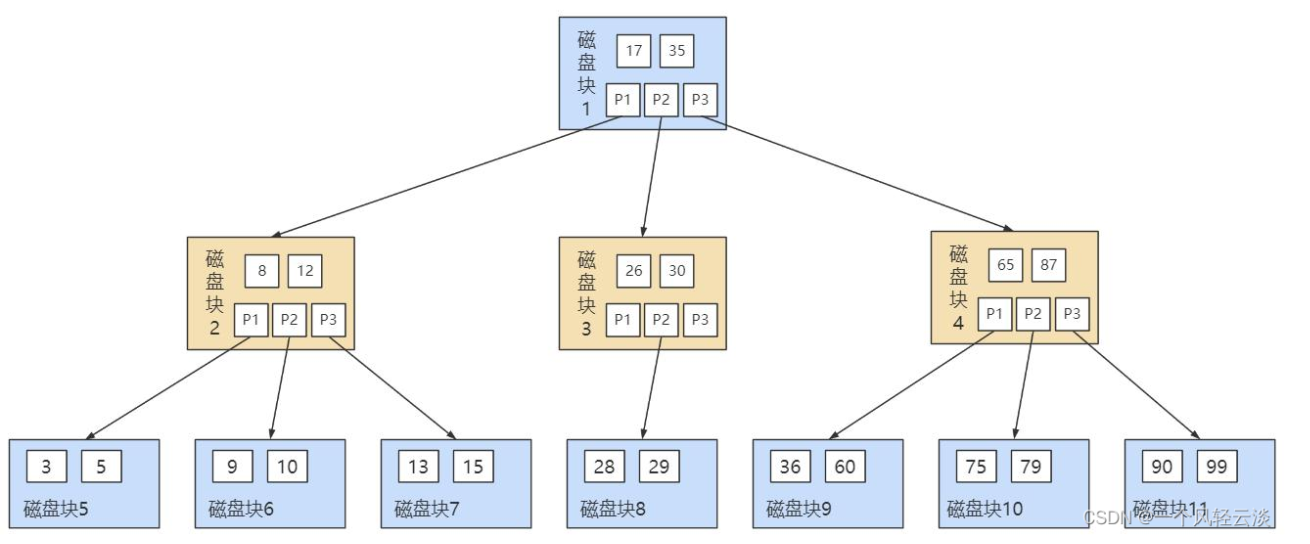
B树的主要特点有:
- B树的节点中存储着多个元素, 每个内节点有多个分叉.
- 在所有的节点中都存储数据
- 父节点当中的元素不会出现在子节点中.
- 所有的叶子节点都位于同一层, 叶子节点具有相同的深度, 叶子节点之间没有指针连接.
上面那张图所表示的 B 树就是一棵 3 阶的 B 树。我们可以看下磁盘块 2,里面的关键字为(8,12),它 有 3 个孩子 (3,5),(9,10) 和 (13,15),你能看到 (3,5) 小于 8,(9,10) 在 8 和 12 之间,而 (13,15)大于 12,刚好符合刚才我们给出的特征。 然后我们来看下如何用 B 树进行查找。假设我们想要 查找的关键字是 9 ,那么步骤可以分为以下几步:
- 我们与根节点的关键字 (17,35)进行比较,9 小于 17 那么得到指针 P1;
- 按照指针 P1 找到磁盘块 2,关键字为(8,12),因为 9 在 8 和 12 之间,所以我们得到指针 P2;
- 按照指针 P2 找到磁盘块 6,关键字为(9,10),然后我们找到了关键字 9。
B 树相比于平衡二叉树来说磁盘 I/O 操作要少 , 在数据查询中比平衡二叉树效率要高。所以 只要树的高度足够低,IO次数足够少,就可以提高查询性能 。
B+树
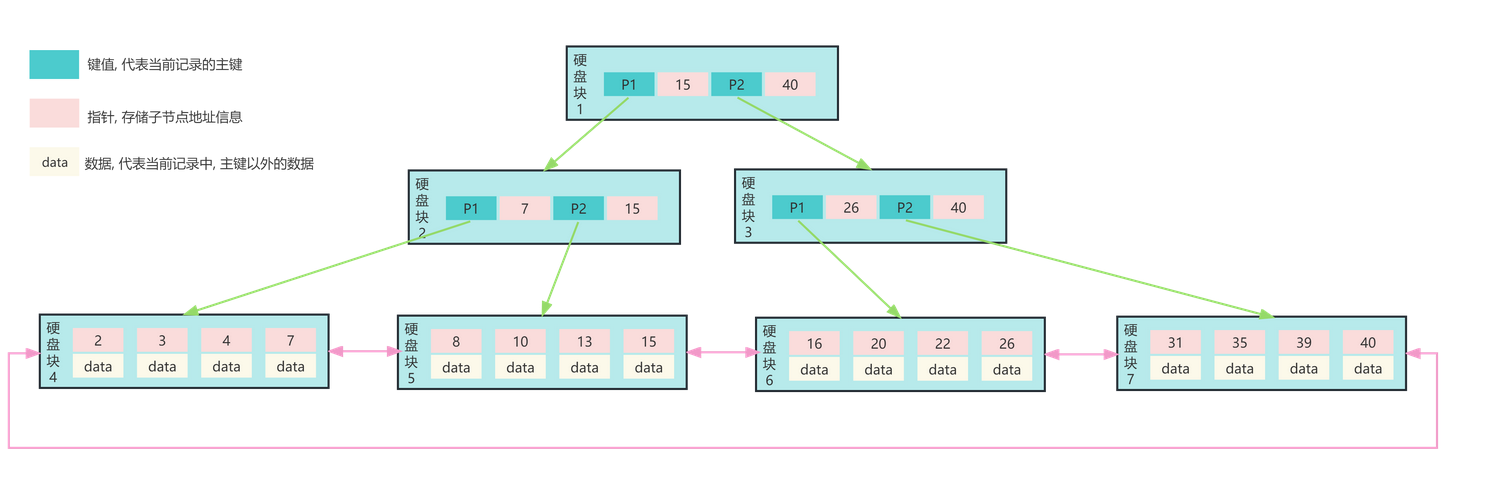
B+树是B树的改造版, 他与B树的不同点有:
- 所有的data在叶子节点出现, 内部节点不再存储data, 只存储key
- 叶子节点之间使用双向指针连接, 最底层的叶子节点形成了一个双向有序链表, 方便进行范围查询.
B+树的查找与B树不同,当索引部分某个节点的关键字与所查的关键字相等时,并不停止查找,应继续沿着这个关键字左边的指针向下,一直查到该关键字所在的叶子节点为止。
B+树可以保证精确查询和范围查询的快速查找,MySQL的innodb存储引擎底层就是B+树.
为什么InnoDB选择B+树而不是B树:
1、B+树的磁盘读取代价低, B树每个节点都有data,B+树只有叶子节才有,假设每个节点大小16KB,那么B+树比B树能存储更多的关键字,一次性读入内存的关键字的内存也会更多,B+树的高度也会比B树低,磁盘IO次数会更少。
2、B+树对范围查询更友好,方便遍历,B树叶子节点没有链接,而B+树叶子节点通过双向指针链接,可以很方便的进行范围查询,比如where条件中 age >= 3 and age < 20,那么当找到3时就可以顺着指针找到20,而B树是不可以的。
3、B+树查询效率稳定性更好, 在B+树中,由于分支节点并不是最终指向文件内容的节点,分支节点只是叶子节点的索引,所以对于任意关键字的查找都必须从根节点走到分支节点,所有关键字查询路径长度相同,每个数据查询效率相当。而对于B树而言,其分支节点上也保存有数据,对于每一个数据的查询所走的路径长度是不一样的,效率也不一样,B树稳定性不如B+树好









![[英语学习][6][Word Power Made Easy]的精读与翻译优化](https://img-blog.csdnimg.cn/direct/16c48dd5b27045869c59ac0c3d73561e.jpeg)
