背景：

实现要求：

1. 根据图的抽象数据类型的定义，请采用邻接矩阵来存储图1，采用邻接表来存储图2，并完成如下操作：
2. 
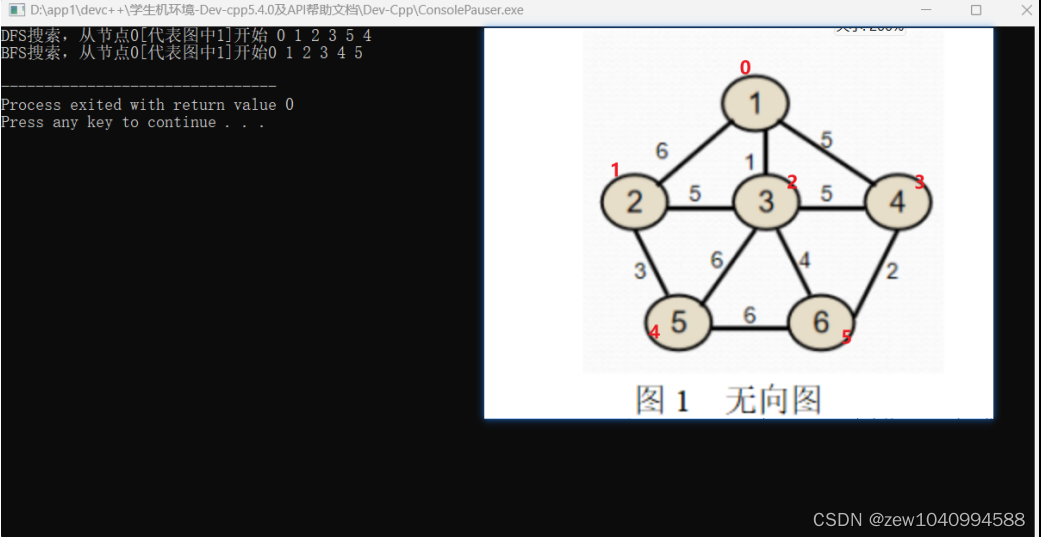
3. 对图1无向图进行深度优先遍历和广度优先遍历。
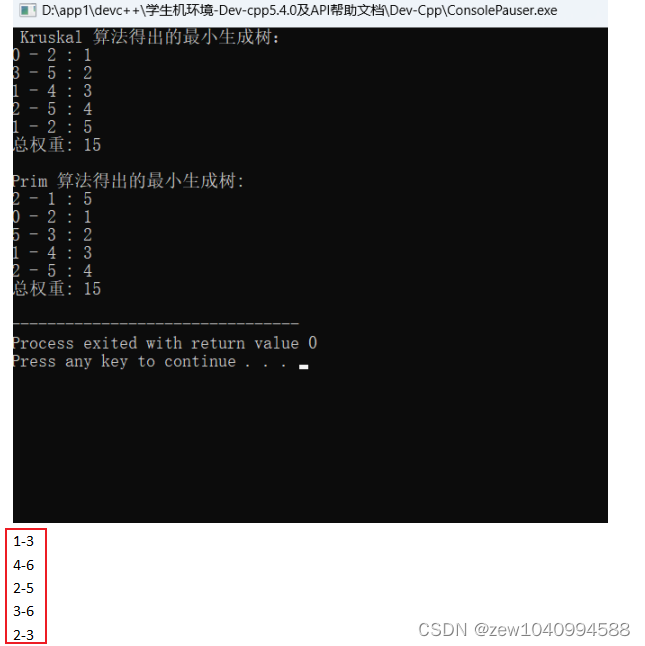
4. 对图1无向图采用Kruskal算法和Prim算法得出最小生成树。
5. 对图2有向图进行拓扑排序，并输出。

实现无向图类和有向图类，编写测试main()函数，实例化无向图类对象和有向图类对象。

2.编制校园导航程序。依托青岛理工大学校园，给出主要建筑的名称信息及有路线连通的建筑之间的距离，抽象为图的数据结构，编程给出从任一建筑出发去校园另一建筑位置的最优路线及其距离。

实现要求：

构建带权有向图，并在附录中给出；

（2）实现Dijkstra算法或者Floyd算法；

（3）程序运行时，给出校园所有建筑物供用户选择，选出起点和终点，给出最短路径及距离。

实现提示：

（3）测试数据（或者自定义其他输入，或者使用文件）。

过程效果：

1-DFS和BFS（对图1无向图进行深度优先遍历和广度优先遍历）：

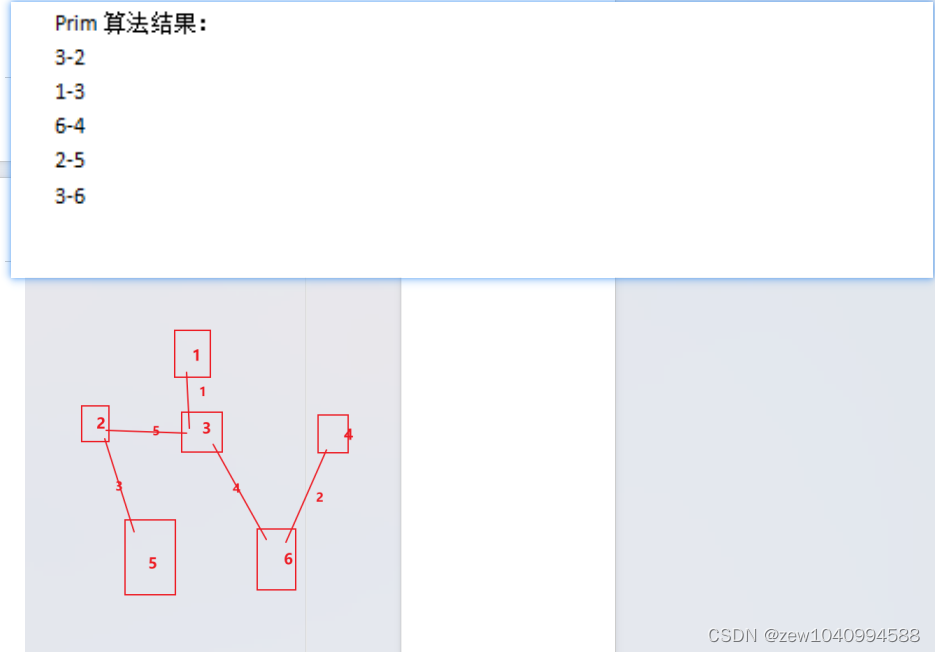
2-对图1无向图采用Kruskal算法和Prim算法得出最小生成树：

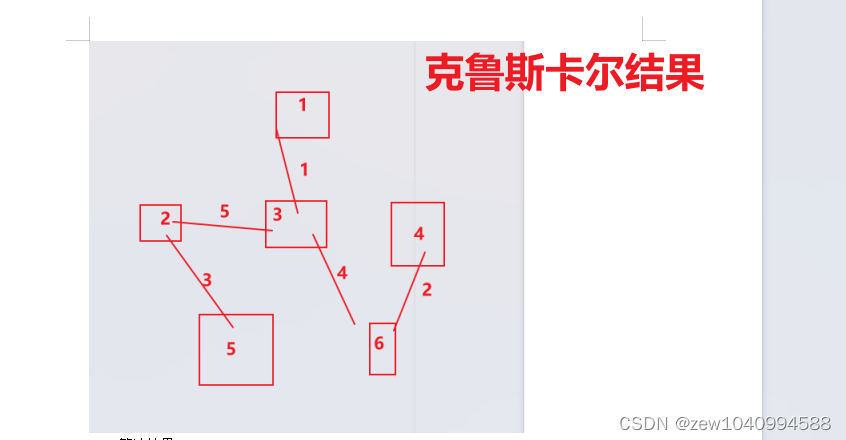
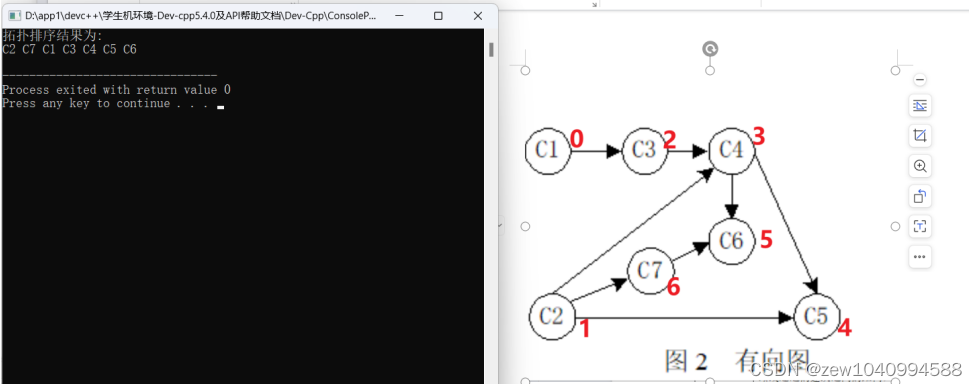
3-对图2有向图进行拓扑排序，并输出：

1. 编写测试main函数
2. ⽤户界⾯能够进⾏交互；

4-：实现Dijkstra算法：

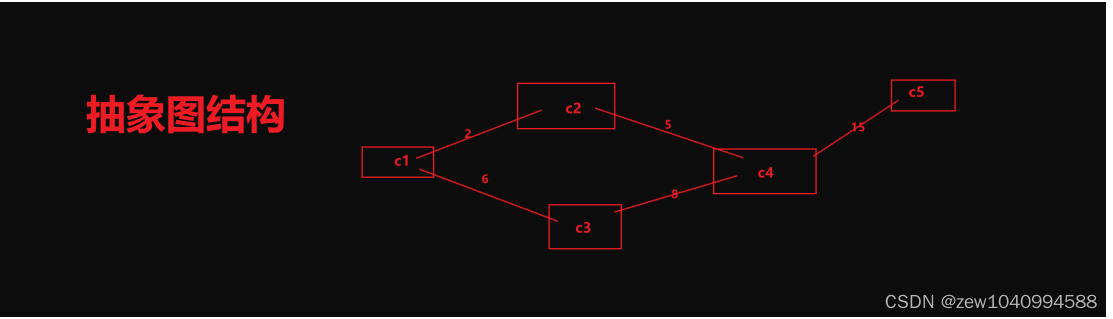
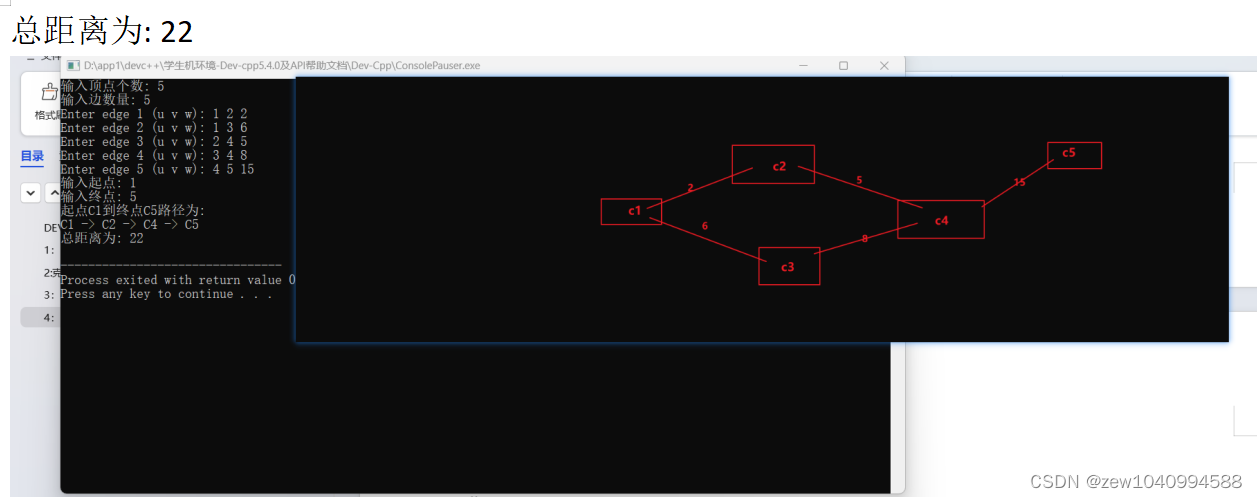
主要代码：

//联系请加V：zew1040994588
//源码获取、定制咨询、非开源

int main() {
    Graph g;
	 
    g.addEdge(0, 1, 6);
    g.addEdge(0, 2, 1);
    g.addEdge(0, 3, 5);
    
    
    g.addEdge(1, 2, 5);
    g.addEdge(2, 3, 5);
    
    g.addEdge(1, 4, 3);
    g.addEdge(2, 4, 6);    
	g.addEdge(2, 5, 4);
    g.addEdge(3, 5, 2);
    
    g.addEdge(4, 5, 6);
	/*
	g.addEdge(0, 1, 4);
    g.addEdge(0, 2, 3);
    g.addEdge(1, 3, 2);
    g.addEdge(1, 4, 7);
    g.addEdge(2, 4, 1);
    g.addEdge(3, 4, 5);
    g.addEdge(3, 5, 6);
    */
    
    cout << "DFS搜索，从节点0[代表图中1]开始 ";
    g.DFS(0);
    cout << endl;

    cout << "BFS搜索，从节点0[代表图中1]开始";
    g.BFS(0);
    cout << endl;

    return 0;
}

//联系请加V：zew1040994588
//源码获取、定制咨询、非开源

int main() {
    Graph g(7);

    g.addEdge(0, 2);
    g.addEdge(2, 3);
    
    g.addEdge(1, 3);
    g.addEdge(1, 6);
    g.addEdge(1, 4);
    
    g.addEdge(3, 5);
    g.addEdge(6, 5);
    g.addEdge(3, 4);

    g.topologicalSort();

    return 0;
}