JAVA代码编写

动态规划（Dynamic Programming）

一个问题可以划分为多个子问题，且子问题之间有关联，就可以使用动态规划。

动态规划问题步骤：

1. 确定dp数组（dp table）以及下标的含义
2. 确定递推公式 d
3. p数组如何初始化
4. 确定遍历顺序
5. 举例推导dp数组

509. 斐波那契数

方法一：动态规划

思路：

状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

class Solution {
    public int fib(int n) {
        ArrayList<Integer> f = new ArrayList<>();
        f.add(0);
        f.add(1);
        for(int i = 2; i<=n; i++){
            f.add(f.get(i-1)+f.get(i-2));
        }
        return f.get(n).intValue();
    }
}

class Solution {
    public int fib(int n) {
        if (n <= 1) return n;             
        int[] dp = new int[n + 1];
        dp[0] = 0;
        dp[1] = 1;
        for (int index = 2; index <= n; index++){
            dp[index] = dp[index - 1] + dp[index - 2];
        }
        return dp[n];
    }
}

思路：

**状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];**每次都重新赋值a和b，这个代码很久以前看过，但自己写写不出来。这里的代码空间复杂度小一点，因为不需要存储所有的结果。

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

class Solution {
    public int fib(int n) {
        if (n < 2) return n;
        int a = 0, b = 1, c = 0;
        for (int i = 1; i < n; i++) {
            c = a + b;
            a = b;
            b = c;
        }
        return c;
    }
}

方法二：递归

思路：

状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

class Solution {
    public int fib(int n) {
        if(n < 2) return n;
        return fib(n-1)+fib(n-2);
    }
}

70. 爬楼梯

输入：n = 2
输出：2
解释：有两种方法可以爬到楼顶。
1. 1 阶 + 1 阶
2. 2 阶

输入：n = 3
输出：3
解释：有三种方法可以爬到楼顶。
1. 1 阶 + 1 阶 + 1 阶
2. 1 阶 + 2 阶
3. 2 阶 + 1 阶

方法一：动态规划

思路：真的很难想到定义

步骤

1. 定义dp数组：dp[i]： 爬到第i层楼梯，有dp[i]种方法

2. 递推公式：dp[i] = dp[i - 1] + dp[i - 2]

   • dp[i - 1]，上i-1层楼梯，有dp[i - 1]种方法，那么再一步跳一个台阶不就是dp[i]了么。
   • dp[i - 2]，上i-2层楼梯，有dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么。
     可以这样理解，这边我看了两三遍才理解。因为每次只能走1个楼梯或两个楼梯，那么我们要走i个楼梯，可以从第i-2个楼梯，再走2个楼梯；也可以从第i-1个楼梯，再走1个楼梯。所以dp[i] = dp[i - 1] + dp[i - 2]

3. dp数组初始化：dp[1]=1,dp[2]=2

4. 确定遍历顺序:根据递推公式，从前往后

5. 举例推导dp数组

   

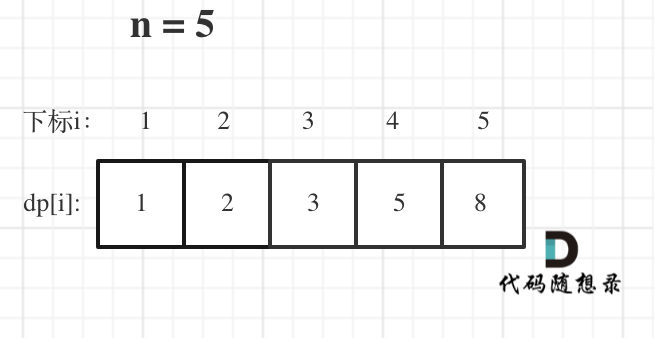
   就是斐波那契数列。

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

class Solution {
    public int climbStairs(int n) {
        ArrayList<Integer> f = new ArrayList<>();
        f.add(0);
        f.add(1);
        for(int i = 2; i<=n+1; i++){
            f.add(f.get(i-1)+f.get(i-2));
        }
        return f.get(n+1).intValue();
    }
}

746. 使用最小花费爬楼梯

输入：cost = [10,15,20]
输出：15
解释：你将从下标为 1 的台阶开始。
- 支付 15 ，向上爬两个台阶，到达楼梯顶部。
总花费为 15 。

输入：cost = [1,100,1,1,1,100,1,1,100,1]
输出：6
解释：你将从下标为 0 的台阶开始。
- 支付 1 ，向上爬两个台阶，到达下标为 2 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 4 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 6 的台阶。
- 支付 1 ，向上爬一个台阶，到达下标为 7 的台阶。
- 支付 1 ，向上爬两个台阶，到达下标为 9 的台阶。
- 支付 1 ，向上爬一个台阶，到达楼梯顶部。
总花费为 6 。

方法一：动态规划1

思路：

步骤

1. 定义dp数组：dp[i]： 爬到第i层楼梯的最低花费

2. 递推公式：dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])

   • dp[i - 1]，到i-1层的最低花费dp[i - 1]，那么再一步跳一个台阶不就是dp[i]了么，那到i的最低花费就是dp[i-1]+cost[i-1]。

   • dp[i - 2]，到i-2层的最低花费dp[i - 2]种方法，那么再一步跳两个台阶不就是dp[i]了么，那到i的最低花费就是dp[i-2]+cost[i-2]。

     所以递推公式就是dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])

3. dp数组初始化：dp[0]=0,dp[1]=0

4. 确定遍历顺序:根据递推公式，从前往后

5. 举例推导dp数组，以cost = [10,15,20]举例

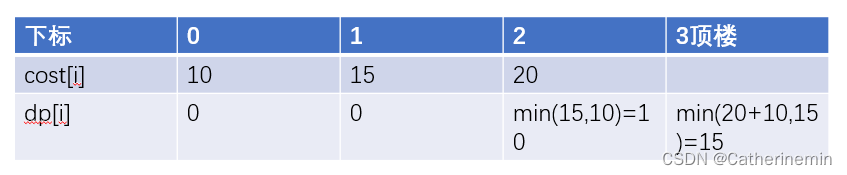
复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length+1];
        dp[0] = 0;
        dp[1] = 0;

        for(int i = 2; i <= cost.length; i++){
            dp[i] =Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);
        }
        return dp[cost.length];
    }
}

方法二：动态规划2

思路：

步骤

1. 定义dp数组：dp[i]： 爬到第i层楼梯的最低花费
2. 递推公式：dp[i] = min(dp[i - 1], dp[i - 2]) + cost[i]
   • 到i层楼梯的最低花费，可以理解为爬第i层所需的消耗+到第i层之前的最低消耗。到第i层之前的最低消耗可以分为dp[i - 1]和dp[i - 2]，因为每次可以走一步或两步。

其他都类似，直接放上卡哥的代码

// 方式二：第一步支付费用
class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[] dp = new int[cost.length];
        dp[0] = cost[0];
        dp[1] = cost[1];
        for (int i = 2; i < cost.length; i++) {
            dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];
        }
        //最后一步，如果是由倒数第二步爬，则最后一步的体力花费可以不用算
        return Math.min(dp[cost.length - 1], dp[cost.length - 2]);
    }
}