代码浅析DLIO(四)---位姿更新

news2024/12/23 6:31:08

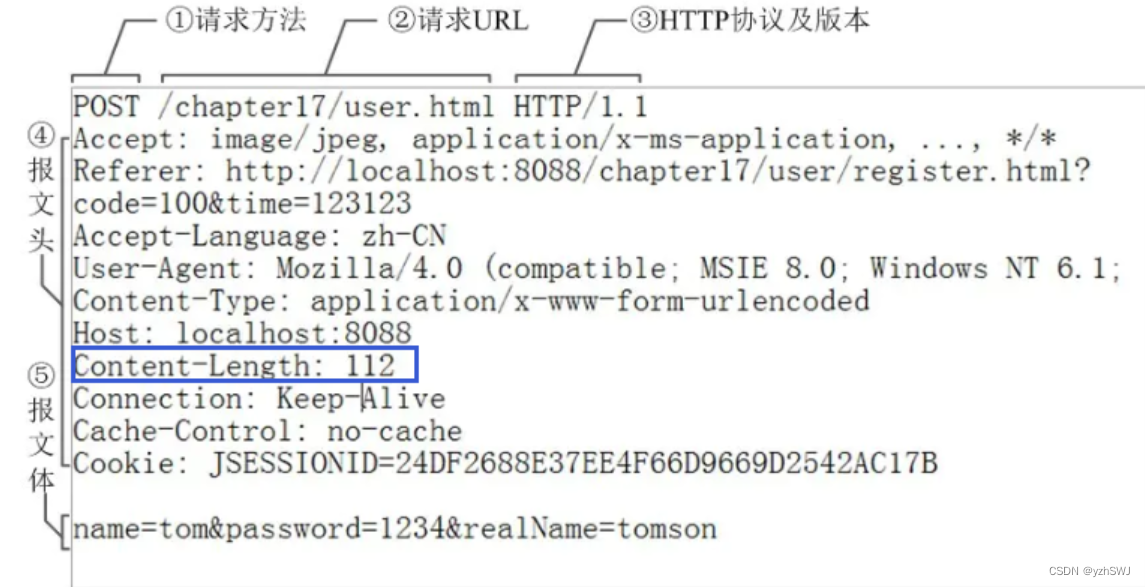
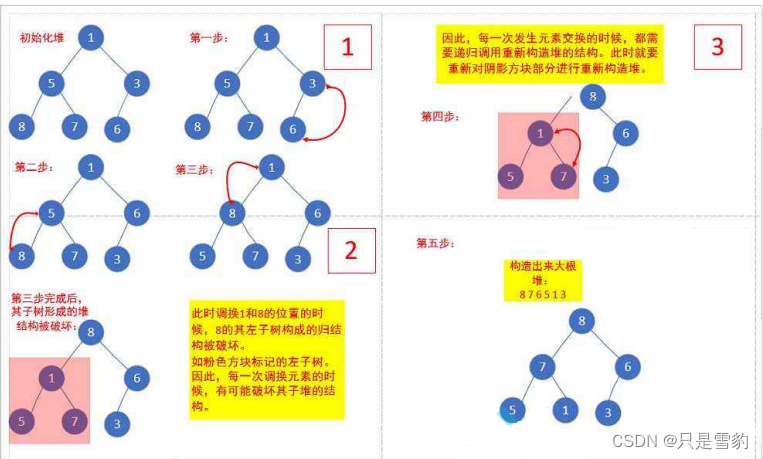
0. 简介

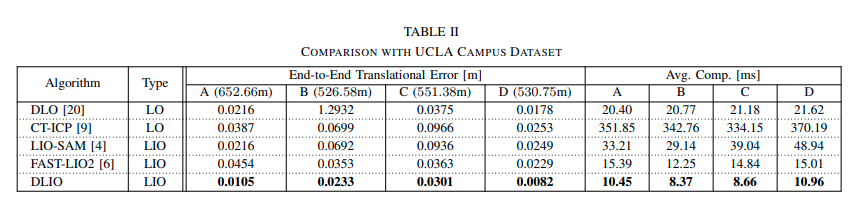
我们刚刚了解过DLIO的整个流程，我们发现相比于Point-LIO而言，这个方法更适合我们去学习理解，同时官方给出的结果来看DLIO的结果明显好于现在的主流方法，当然指的一提的是，这个DLIO是必须需要六轴IMU的，所以如果没有IMU的画，那只有DLO可以使用了。

在这里插入图片描述

1. getNextPose–通过IMU + S2M + GEO获取下一个姿态

下面的函数作用主要是获取下一个姿态的函数，主要是通过IMU、S2M和GEO三种方式获取。首先，检查新子地图是否准备就绪，如果准备好了并且子地图发生了变化，则将当前全局子地图设置为目标点云，并设置子图的kdtree以及将目标云的法线设置为子地图的法线。接着，使用全局IMU变换作为初始猜测，将当前子地图与全局地图对齐，并在全局坐标系中获取最终变换。然后，更新下一个全局位姿，并进行几何观察器更新。最终，该函数返回下一个姿态。

/**
 * @brief 通过IMU + S2M + GEO获取下一个姿态
 *
 */
void dlio::OdomNode::getNextPose() {

  // 检查新子地图是否准备好可供使用
  this->new_submap_is_ready =
      (this->submap_future.wait_for(std::chrono::seconds(0)) ==
       std::future_status::ready); //等待子地图准备好

  if (this->new_submap_is_ready &&
      this->submap_hasChanged) { //如果子地图准备好了,并且子地图发生了变化

    // 将当前全局子地图设置为目标点云
    this->gicp.registerInputTarget(this->submap_cloud);

    // 设置子图的kdtree,之前就是直接从target_kdtree_拿出来的,这个有必要嘛?
    this->gicp.target_kdtree_ = this->submap_kdtree;

    // 将目标云的法线设置为子地图的法线
    this->gicp.setTargetCovariances(this->submap_normals);

    this->submap_hasChanged = false;
  }

  // 使用全局IMU变换作为初始猜测，将当前子地图与全局地图对齐
  pcl::PointCloud<PointType>::Ptr aligned(
      boost::make_shared<pcl::PointCloud<PointType>>());
  this->gicp.align(*aligned); // 设置对齐后的地图

  // 在全局坐标系中获取最终变换
  this->T_corr =
      this->gicp.getFinalTransformation(); // 根据对齐后的地图来校准转换
  this->T = this->T_corr * this->T_prior;

  // 更新下一个全局位姿,现在源点云和目标点云都在全局坐标系中，所以变换是全局的
  this->propagateGICP();

  // 几何观察器更新
  this->updateState();
}

2. updateState–更新GEO信息

这段代码是通过GEO更新状态的，主要分为以下几个步骤：

  1. 锁定线程以防止状态被PropagateState访问，保证线程安全。
  2. 获取机器人当前的位置、四元数和时间差。
  3. 通过拿到的四元数和预测的四元数构造误差的四元数，然后根据误差的四元数构建四元数校正量，对应公式7。
  4. 将误差的四元数转换到机器人的body坐标系下。
  5. 更新加速度偏差和陀螺仪偏差，同时限制偏差的最大值。
  6. 更新机器人的速度和位置，以及四元数，同时存储前一个姿态、方向和速度。
void dlio::OdomNode::updateState() {

  // 锁定线程以防止状态被PropagateState访问
  std::lock_guard<std::mutex> lock(this->geo.mtx);

  Eigen::Vector3f pin = this->lidarPose.p;              // 位置
  Eigen::Quaternionf qin = this->lidarPose.q;           // 四元数
  double dt = this->scan_stamp - this->prev_scan_stamp; // 时间差

  Eigen::Quaternionf qe, qhat, qcorr;
  qhat = this->state.q;

  // 构造误差的四元数
  qe = qhat.conjugate() * qin; //通过拿到的四元数和预测的四元数构造误差的四元数

  double sgn = 1.;
  if (qe.w() < 0) { // 如果误差的四元数的w小于0
    sgn = -1;
  }

  // 构建四元数校正量,对应公式7
  qcorr.w() = 1 - abs(qe.w());  // 误差的四元数的w部分
  qcorr.vec() = sgn * qe.vec(); // 误差的四元数的向量部分
  qcorr = qhat * qcorr;         // 误差的四元数

  Eigen::Vector3f err = pin - this->state.p;
  Eigen::Vector3f err_body;

  err_body =
      qhat.conjugate()._transformVector(err); // 误差的四元数转换到body坐标系下

  double abias_max = this->geo_abias_max_;
  double gbias_max = this->geo_gbias_max_;

  // 更新加速度偏差
  this->state.b.accel -= dt * this->geo_Kab_ * err_body;
  this->state.b.accel =
      this->state.b.accel.array().min(abias_max).max(-abias_max);

  // 更新陀螺仪偏差
  this->state.b.gyro[0] -= dt * this->geo_Kgb_ * qe.w() * qe.x();
  this->state.b.gyro[1] -= dt * this->geo_Kgb_ * qe.w() * qe.y();
  this->state.b.gyro[2] -= dt * this->geo_Kgb_ * qe.w() * qe.z();
  this->state.b.gyro =
      this->state.b.gyro.array().min(gbias_max).max(-gbias_max);

  // 更新速度和位置
  this->state.p += dt * this->geo_Kp_ * err;
  this->state.v.lin.w += dt * this->geo_Kv_ * err;

  this->state.q.w() += dt * this->geo_Kq_ * qcorr.w();
  this->state.q.x() += dt * this->geo_Kq_ * qcorr.x();
  this->state.q.y() += dt * this->geo_Kq_ * qcorr.y();
  this->state.q.z() += dt * this->geo_Kq_ * qcorr.z();
  this->state.q.normalize();

  // 存储前一个姿态、方向和速度
  this->geo.prev_p = this->state.p;
  this->geo.prev_q = this->state.q;
  this->geo.prev_vel = this->state.v.lin.w;
}

3. updateKeyframes–更新关键帧

在做完位置更新后就会更新关键帧，通过计算当前姿态与轨迹中所有关键帧姿态的差异，然后根据距离和旋转角度是否超过一定阈值来判断是否需要更新关键帧。具体实现过程如下：

首先，遍历轨迹中所有关键帧，计算当前姿态与每个关键帧之间的距离，并记录最近的关键帧的索引和距离。同时，计算当前姿态附近的关键帧数量。

然后，获取最近关键帧的姿态和旋转，并计算当前姿态与最近关键帧之间的距离和旋转角度。如果旋转角度超过了设定的阈值，或者距离超过了设定的阈值且附近关键帧数量小于等于1，则认为需要更新关键帧。

最后，如果需要更新关键帧，则将当前姿态和点云、时间戳、法向量、变换矩阵等信息存储到关键帧向量中。

整个函数实现了关键帧的自适应更新，可以在SLAM系统中提高精度和效率。

void dlio::OdomNode::updateKeyframes() {

  // 计算轨迹中所有姿态和旋转的差异
  float closest_d = std::numeric_limits<float>::infinity();
  int closest_idx = 0;
  int keyframes_idx = 0;

  int num_nearby = 0;

  for (const auto &k : this->keyframes) {

    // 计算当前姿态与关键帧中的姿态之间的距离,这里和更新submap的操作一样
    float delta_d = sqrt(pow(this->state.p[0] - k.first.first[0], 2) +
                         pow(this->state.p[1] - k.first.first[1], 2) +
                         pow(this->state.p[2] - k.first.first[2], 2));

    //计算当前姿态附近的数量
    if (delta_d <= this->keyframe_thresh_dist_ * 1.5) {
      ++num_nearby;
    }

    // 将其存储到变量中
    if (delta_d < closest_d) {
      closest_d = delta_d;         //最近的距离
      closest_idx = keyframes_idx; //最近的关键帧的索引
    }

    keyframes_idx++;
  }

  // 获取最接近的姿势和相应的旋转
  Eigen::Vector3f closest_pose =
      this->keyframes[closest_idx].first.first; //最近的关键帧的位置
  Eigen::Quaternionf closest_pose_r =
      this->keyframes[closest_idx].first.second; //最近的关键帧的旋转

  // 计算当前姿势与最近的姿势之间的距离,和closest_d一致
  float dd = sqrt(pow(this->state.p[0] - closest_pose[0], 2) +
                  pow(this->state.p[1] - closest_pose[1], 2) +
                  pow(this->state.p[2] - closest_pose[2], 2));

  // 使用SLERP计算方向差异
  Eigen::Quaternionf dq;

  if (this->state.q.dot(closest_pose_r) <
      0.) { //如果两个四元数的点积小于0，说明两个四元数的方向相反
    Eigen::Quaternionf lq = closest_pose_r; //将最近的关键帧的旋转赋值给lq
    lq.w() *= -1.;
    lq.x() *= -1.;
    lq.y() *= -1.;
    lq.z() *= -1.;
    dq = this->state.q * lq.inverse(); //计算当前姿态与最近的姿态之间的旋转
  } else {
    dq = this->state.q *
         closest_pose_r.inverse(); //计算当前姿态与最近的姿态之间的旋转
  }

  double theta_rad =
      2. * atan2(sqrt(pow(dq.x(), 2) + pow(dq.y(), 2) + pow(dq.z(), 2)),
                 dq.w()); //计算当前姿态与最近的姿态之间的旋转角度
  double theta_deg = theta_rad * (180.0 / M_PI); //将弧度转换为角度

  // 更新关键帧
  bool newKeyframe = false;

  if (abs(dd) > this->keyframe_thresh_dist_ ||
      abs(theta_deg) >
          this->keyframe_thresh_rot_) { //如果距离或者旋转角度超过阈值
    newKeyframe = true;
  }

  if (abs(dd) <= this->keyframe_thresh_dist_ &&
      abs(theta_deg) > this->keyframe_thresh_rot_ &&
      num_nearby <=
          1) { //如果距离小于阈值，但是旋转角度超过阈值，且附近的关键帧数量小于等于1
    newKeyframe = true;
  }

  if (abs(dd) <= this->keyframe_thresh_dist_) { //如果距离小于阈值
    newKeyframe = false;
  } else if (abs(dd) <= 0.5) {
    newKeyframe = false;
  }

  if (newKeyframe) {

    // 更新关键帧向量
    std::unique_lock<decltype(this->keyframes_mutex)> lock(
        this->keyframes_mutex);
    this->keyframes.push_back(std::make_pair(
        std::make_pair(this->lidarPose.p, this->lidarPose.q),
        this->current_scan)); //将当前的姿态和点云压入到keyframes中
    this->keyframe_timestamps.push_back(
        this->scan_header_stamp); //将当前的时间戳压入到keyframe_timestamps中
    this->keyframe_normals.push_back(
        this->gicp
            .getSourceCovariances()); //将当前的法向量压入到keyframe_normals中
    this->keyframe_transformations.push_back(
        this->T_corr); //将当前的变换矩阵压入到keyframe_transformations中
    lock.unlock();
  }
}

4. propagateState–传播GEO状态

然后我们整个基本都过完了，只有一个IMU的feedback中漏掉的propagateState函数。通过IMU测量值来更新机器人的状态。首先通过一个mutex锁来确保线程安全。然后获取IMU测量的时间间隔，并将当前状态下的四元数和角速度赋值给变量qhat和omega。接下来将机体坐标系下的加速度转换到世界坐标系下，并使用加速度传播公式更新机器人的位置和速度。同时，将机器人的角速度更新为世界坐标系下的角速度。然后使用重力计传播公式更新四元数，确保其归一化。最后，将机器人的角速度和四元数更新到状态中。

…详情请参照古月居

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1277852.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

面试就是这么简单，offer拿到手软（一）—— 常见非技术问题回答思路

面试就是这么简单，offer拿到手软（一）—— 常见非技术问题回答思路

面试系列&#xff1a; 面试就是这么简单&#xff0c;offer拿到手软&#xff08;一&#xff09;—— 常见非技术问题回答思路 面试就是这么简单&#xff0c;offer拿到手软&#xff08;二&#xff09;—— 常见65道非技术面试问题 文章目录 一、前言二、常见面试问题回答思路问…
阅读更多...
webGIS使用JS,高德API完成简单的智慧校园项目基础

webGIS使用JS,高德API完成简单的智慧校园项目基础

代码实现 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-width, i…
阅读更多...
react之@路径解析配置和联想配置

react之@路径解析配置和联想配置

react之路径解析配置和联想配置 一、介绍二、路径解析配置三、联想路径配置 一、介绍 1.路径解析配置&#xff08;webpack&#xff09;&#xff0c;把 / 解析为 src/2.路径联想配置&#xff08;VsCode&#xff09;&#xff0c;VsCode 在输入 / 时&#xff0c;自动联想出来对应…
阅读更多...
ARM64版本的chrome浏览器安装

ARM64版本的chrome浏览器安装

这一快比较玄学&#xff0c;花个半个小时左右才能安装好&#xff0c;也不知道是个什么情况。 sudo snap install chromium只需要以上这个命令&#xff0c;当然&#xff0c;也可以自己去找安装包进行安装&#xff0c;但是测试后发现并没有那么好装&#xff0c;主要是两个部分 一…
阅读更多...
Halcon参考手册目标检测和实例分割知识总结

Halcon参考手册目标检测和实例分割知识总结

1.1 目标检测原理介 目标检测&#xff1a;我们希望找到图像中的不同实例并将它们分配给某一个类别。实例可以部分重叠&#xff0c;但仍然可以区分为不同的实例。如图(1)所示&#xff0c;在输入图像中找到三个实例并将其分配给某一个类别。 图(1)目标检测示例 实例分割是目标检…
阅读更多...
打造个性化github主页 一

打造个性化github主页 一

文章目录 概述创建仓库静态美化GitHub 统计信息卡仓库 GitHub 额外图钉仓库 热门语言卡仓库 GitHub 资料奖杯仓库 GitHub 活动统计图仓库 打字特效添加中文网站统计仓库 总结 概述 github作为全球最大的代码托管平台&#xff0c;作为程序员都多多少少&#xff0c;都使用过他。…
阅读更多...
基于SpringBoot的公益慈善平台

基于SpringBoot的公益慈善平台

✌全网粉丝20W,csdn特邀作者、博客专家、CSDN新星计划导师、java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ &#x1f345;文末获取项目下载方式&#x1f345; 一、项目背景介绍&#xff1a; 基于SpringBoot的公益…
阅读更多...
【上海大学数字逻辑实验报告】三、组合电路（二）

【上海大学数字逻辑实验报告】三、组合电路（二）

一、实验目的 掌握8421码到余3码的转换。掌握2421码到格雷码的转换。进一步熟悉组合电路的分析和设计方法。学会使用Quartus II设计8421码到余3码的转换电路逻辑图。学会使用Quartus II设计2421码到格雷码的转换电路逻辑图。 二、实验原理 8421码是最常用的BCD码&#xff0c…
阅读更多...
YOLOv5算法进阶改进（7）— 将主干网络SPPF更换为SimSPPF / SPP-CSPC / SPPF-CSPC

YOLOv5算法进阶改进（7）— 将主干网络SPPF更换为SimSPPF / SPP-CSPC / SPPF-CSPC

前言：Hello大家好，我是小哥谈。SimSPPF是YOLOv6中提出的一种改进的空间金字塔池化方法，它是SPPF的升级版。SimSPPF通过在不同尺度上使用不同大小的池化核来提取特征，从而提高了检测器的性能。与SPPF相比，SimSPPF可以在不增加计算成本的情况下提高检测器的性能。本节课就教…
阅读更多...
Nacos源码解读01——服务注册

Nacos源码解读01——服务注册

Nacos 2.0 架构设计及新模型 参考 https://zhuanlan.zhihu.com/p/344572647 使用GRPC注册临时实例流程图 SpringBoot自动注入 注入对应服务注册的Bean 监听Tomcat启动事件 NacosAutoServiceRegistration 继承了AbstractAutoServiceRegistration 而 AbstractAutoServiceR…
阅读更多...
Oracle忘记所有密码怎么办

Oracle忘记所有密码怎么办

最近遇到一个Oracle的问题&#xff0c;密码要过期了&#xff0c;但是除了用户密码&#xff0c;其他密码都不知道了&#xff0c;修改不了密码怎么办呢&#xff1f; 试了各种方法&#xff0c;最终下面的方式生效了&#xff1a; 首先&#xff0c;使用orapwd生成新的密码文件&…
阅读更多...
NIO网络编程

NIO网络编程

Netty学习之NIO基础 - Nyimas Blog 1、阻塞 阻塞模式下&#xff0c;相关方法都会导致线程暂停 ServerSocketChannel.accept 会在没有连接建立时让线程暂停SocketChannel.read 会在通道中没有数据可读时让线程暂停阻塞的表现其实就是线程暂停了&#xff0c;暂停期间不会占用 c…
阅读更多...
说一说Java中的JUC

说一说Java中的JUC

JUC 1.什么是JUC 2.进程和线程 进程 : cpu资源分配的最小单位 线程 : cpu调度和执行的最小单位 并发是指多个任务在同一个时间段内交替执行&#xff0c;通过时间片轮转等方式实现任务间的切换。换句话说&#xff0c;并发是指多个任务能够同时存在&#xff0c;但不一定同时…
阅读更多...
树和二叉树的基本概念和堆的实现

树和二叉树的基本概念和堆的实现

树的概念及结构 树的概念 树是一种非线性的数据结构&#xff0c;它是由n&#xff08;n>0&#xff09;个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树&#xff0c;也就是说它是根朝上&#xff0c;而叶朝下的。 1.有一个特殊的结点&#…
阅读更多...
深度学习 -- 卷积神经网络

深度学习 -- 卷积神经网络

1、卷积神经网络的结构 大卫休伯尔( David Hunter Hubel ) 等人研究发现&#xff0c;猫的视皮层上 存在简单细胞( simple cell )和复杂细胞( complex cell )&#xff0c;简单细胞会对 感受野中特定朝向的线段做出反应&#xff0c;而复杂细胞对于特定朝向的钱段移动也能做出反应…
阅读更多...
使用mybatis-plus框架：@Autowired报错Could not autowire. No beans of ‘XXX‘ type found

使用mybatis-plus框架：@Autowired报错Could not autowire. No beans of ‘XXX‘ type found

使用mybatis-plus框架,使用xxmapper报错&#xff1a; 解决办法是&#xff1a;在mapper中添加注解&#xff1a; Repository Mapper 也可以使用 AutowiredSysRoleMenuService sysRoleMenuService;替代 AutowiredSysRoleMenuMapper sysRoleMenuMapper;方法名不同&#xff0c;但…
阅读更多...
工业机器视觉megauging（向光有光）使用说明书（十三，资源发现bug，已经更新）

工业机器视觉megauging（向光有光）使用说明书（十三，资源发现bug，已经更新）

megauging&#xff08;向光有光&#xff09;旧资源有bug&#xff0c;已经更新&#xff0c;如下&#xff1a; 第一工具&#xff0c;combox默认0&#xff0c;选择后&#xff0c;鼠标点击“获取结果”&#xff0c;相机就取一帧图像处理后显示出来&#xff1a; 第一工具&#xff0…
阅读更多...
计算机网络之网络传输，三次握手和四次挥手

计算机网络之网络传输，三次握手和四次挥手

网络传输通过高低电压 流 基本类型数组 低电压转高电压&#xff0c;通过网卡 传输模式&#xff1a; 全双工&#xff1a;互相传输且能同时传输 半双工&#xff1a;互相传输但是不能同时传输 单工&#xff1a;单向传输&#xff0c;&#xff08;键盘&#xff0c;显示器&#…
阅读更多...
LIN TP

LIN TP

LIN总线为了解决多帧场景&#xff0c;也像CAN一样有TP协议。 主机发送请求PDU&#xff0c;从机发送应答PDU。 分为单帧(Single Frame&#xff0c;SF)、首帧(First Frame&#xff0c;FF)和续帧(Consecutive Frames&#xff0c;CF)三种。 PDU结构 包含节点地址(NAD)、协议控制…
阅读更多...
C语言-预处理与库

C语言-预处理与库

预处理、动态库、静态库 1. 声明与定义分离 一个源文件对应一个头文件 注意&#xff1a; 头文件名以 .h 作为后缀头文件名要与对应的原文件名 一致 例&#xff1a; 源文件&#xff1a;01_code.c #include <stdio.h> int num01 10; int num02 20; void add(int a, in…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023