一、介绍

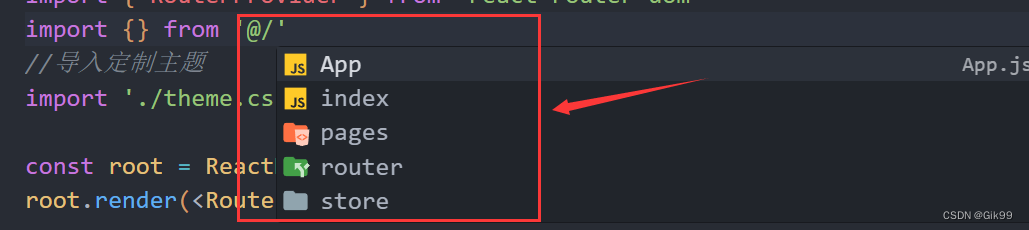
• 1.路径解析配置（webpack），把 @/ 解析为 src/
• 2.路径联想配置（VsCode），VsCode 在输入 @/ 时，自动联想出来对应的 src/下的子级目录

二、路径解析配置

• 1.安装craco

npm i craco

• 2.项目根目录下创建配置文件 craco.config.js

const path = require('path')

module.exports = {
  //webpack配置
  webpack: {
    //配置别名
    alias: {
      //约定:使用@标识src文件所在路径
      '@': path.resolve(__dirname, 'src'),
    },
  },
}

• 3.包文件中配置启动和打包命令 package.json

"scripts": {
    "start": "craco start",
    "build": "craco build",
  },

三、联想路径配置

• 根目录下新增配置文件 - jsconfig.json

  {
      "compilerOptions":{
        "baseUrl":"./",
        "paths":{
          "@/*":[
            "src/*"
          ]
        }
      }
    }

• 实现效果