深度优先搜索和广度优先搜索
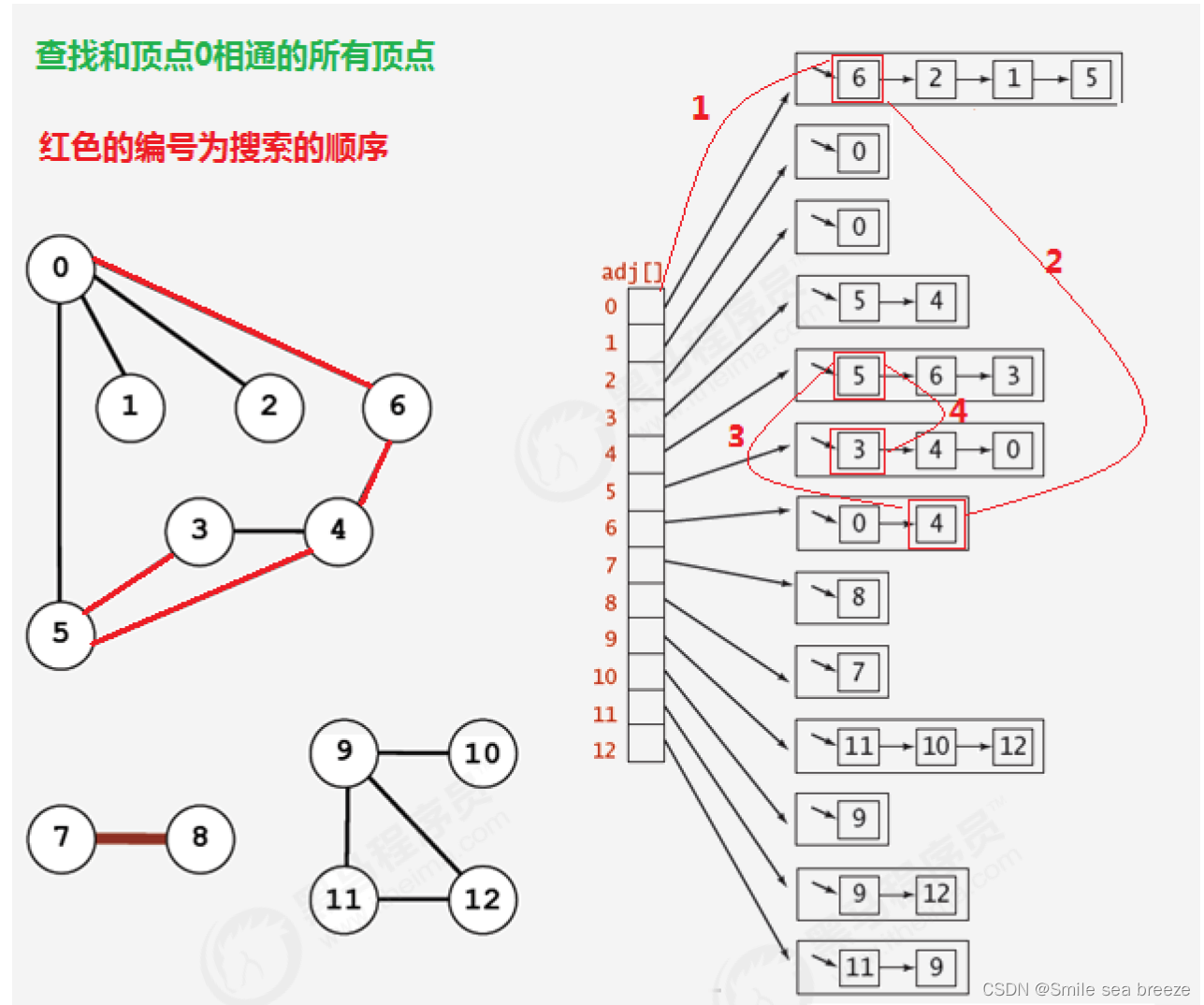
在很多情况下,我们需要遍历图,得到图的一些性质,例如,找出图中与指定的顶点相连的所有顶点,或者判定某个顶点与指定顶点是否相通,是非常常见的需求。
有关图的搜索,最经典的算法有深度优先搜索和广度优先搜索,接下来我们分别讲解这两种搜索算法。
1. 深度优先搜索
1.1 定义
所谓的深度优先搜索,指的是在搜索时,如果遇到一个结点既有子结点,又有兄弟结点,那么先找子结点,然后找兄弟结点。
1.2 API设计
| 类名 | DepthFirstSearch |
|---|---|
| 构造方法 | DepthFirstSearch(Graph G,int s):构造深度优先搜索对象,使用深度优先搜索找出G图中s顶点的所有相通顶点 |
| 成员方法 | 1.private void dfs(Graph G, int v):使用深度优先搜索找出G图中v顶点的所有相通顶点 2.public boolean marked(int w):判断w顶点与s顶点是否相通 3.public int count():获取与顶点s相通的所有顶点的总数 |
| 成员变量 | 1.private boolean[] marked: 索引代表顶点,值表示当前顶点是否已经被搜索 2.private int count:记录有多少个顶点与s顶点相通 |
1.3 代码实现
注意:在类中导入自己写的Queue,代码如下
import java.util.Iterator;
public class Queue<T> implements Iterable<T>{
//记录首结点
private Node head;
//记录最后一个结点
private Node last;
//记录队列中元素的个数
private int N;
private class Node{
public T item;
public Node next;
public Node(T item, Node next) {
this.item = item;
this.next = next;
}
}
public Queue() {
this.head = new Node(null,null);
this.last=null;
this.N=0;
}
//判断队列是否为空
public boolean isEmpty(){
return N==0;
}
//返回队列中元素的个数
public int size(){
return N;
}
//向队列中插入元素t
public void enqueue(T t){
if (last==null){
//当前尾结点last为null
last= new Node(t,null);
head.next=last;
}else {
//当前尾结点last不为null
Node oldLast = last;
last = new Node(t, null);
oldLast.next=last;
}
//元素个数+1
N++;
}
//从队列中拿出一个元素
public T dequeue(){
if (isEmpty()){
return null;
}
Node oldFirst= head.next;
head.next=oldFirst.next;
N--;
//因为出队列其实是在删除元素,因此如果队列中的元素被删除完了,需要重置last=null;
if (isEmpty()){
last=null;
}
return oldFirst.item;
}
@Override
public Iterator<T> iterator() {
return new QIterator();
}
private class QIterator implements Iterator{
private Node n;
public QIterator(){
this.n=head;
}
@Override
public boolean hasNext() {
return n.next!=null;
}
@Override
public Object next() {
n = n.next;
return n.item;
}
}
}
public class DepthFirstSearch {
public static void main(String[] args) {
//准备Graph对象
Graph G = new Graph(13);
G.addEdge(0,5);
G.addEdge(0,1);
G.addEdge(0,2);
G.addEdge(0,6);
G.addEdge(5,3);
G.addEdge(5,4);
G.addEdge(3,4);
G.addEdge(4,6);
G.addEdge(7,8);
G.addEdge(9,11);
G.addEdge(9,10);
G.addEdge(9,12);
G.addEdge(11,12);
DepthFirstSearch search = new DepthFirstSearch(G,0);
int count = search.count();
System.out.println("与起点0相同的顶点的数量为:" + count);
boolean marked1 = search.marked(5);
System.out.println("顶点5和0是否相通:" + marked1);
boolean marked2 = search.marked(7);
System.out.println("顶点7和0是否相通:" + marked2);
}
private boolean[] marked; //索引代表顶点,值表示当前顶点是否已经被搜索
private int count;//记录有多少个顶点与s顶点相通
public DepthFirstSearch(Graph G, int s){//构造深度优先搜索对象,使用深度优先搜索找出G图中s顶点的所有相邻顶点
marked = new boolean[G.V()];//创建一个和图的顶点数一样大小的布尔数组
dfs(G,s);//搜索G图中与顶点s相同的所有顶点
}
private void dfs(Graph G, int v){//使用深度优先搜索找出G图中v顶点的所有相邻顶点
marked[v]=true;//把当前顶点标记为已搜索
for(Integer w: G.adj(v)){//遍历v顶点的邻接表,得到每一个顶点w
if(!marked[w]){//如果当前顶点w没有被搜索过,则递归搜索与w顶点相通的其他顶点
dfs(G,w);
}
}
count++;//相通的顶点数量+1
}
public boolean marked(int w)//判断w顶点与s顶点是否相通
{
return marked[w];
}
public int count(){ //获取与顶点s相通的所有顶点的总数
return count;
}
public static class Graph {
private final int V;// 顶点数目
private int E;// 边的数目
private Queue<Integer>[] adj;// 邻接表
public Graph(int V) {
this.V = V;//初始化顶点数量
this.E = 0;//初始化边的数量
this.adj = (Queue<Integer>[]) new Queue[V];// 创建邻接表
for (int i = 0; i < adj.length; i++) {//初始化邻接表中的空队列
adj[i]= new Queue<Integer>() ;
}
}
public int V() {//获取顶点数目
return V;
}
public int E() {//获取边的数目
return E;
}
public void addEdge(int v, int w) {
//把w添加到v的链表中,这样顶点v就多了一个相邻点w
adj[v].enqueue(w);
//把v添加到w的链表中,这样顶点w就多了一个相邻点v
adj[w].enqueue(v);
//边的数目自增1
E++;
}
public Queue<Integer> adj(int v) { //获取和顶点v相邻的所有顶点
return adj[v];
}
}
1.4 运行结果
与起点0相同的顶点的数量为:7
顶点5和0是否相通:true
顶点7和0是否相通:false
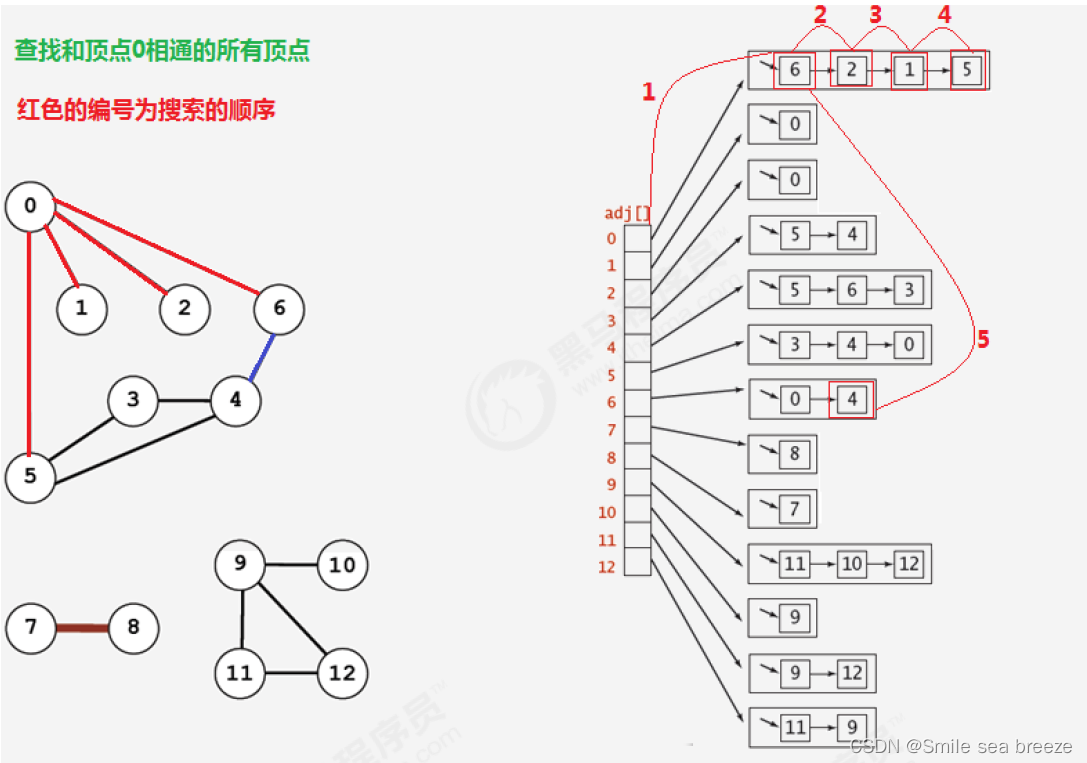
2. 广度优先搜索
2.1 定义
所谓的深度优先搜索,指的是在搜索时,如果遇到一个结点既有子结点,又有兄弟结点,那么先找兄弟结点,然后找子结点。
2.2 API设计
| 类名 | BreadthFirstSearch |
|---|---|
| 构造方法 | BreadthFirstSearch(Graph G,int s):构造广度优先搜索对象,使用广度优先搜索找出G图中s顶点的所有相邻顶点 |
| 成员方法 | 1.private void bfs(Graph G, int v):使用广度优先搜索找出G图中v顶点的所有相邻顶点 2.public boolean marked(int w):判断w顶点与s顶点是否相通 3.public int count():获取与顶点s相通的所有顶点的总数 |
| 成员变量 | 1.private boolean[] marked: 索引代表顶点,值表示当前顶点是否已经被搜索 2.private int count:记录有多少个顶点与s顶点相通 3.private Queue waitSearch: 用来存储待搜索邻接表的点 |
2.3 代码实现
package heimadatapractise;
public class BreadthFirstSearch {
public static void main(String[] args) {
//准备Graph对象
Graph G = new Graph(13);
G.addEdge(0,5);
G.addEdge(0,1);
G.addEdge(0,2);
G.addEdge(0,6);
G.addEdge(5,3);
G.addEdge(5,4);
G.addEdge(3,4);
G.addEdge(4,6);
G.addEdge(7,8);
G.addEdge(9,11);
G.addEdge(9,10);
G.addEdge(9,12);
G.addEdge(11,12);
BreadthFirstSearch search = new BreadthFirstSearch(G,0);
int count = search.count();
System.out.println("与起点0相同的顶点的数量为:" + count);
boolean marked1 = search.marked(5);
System.out.println("顶点5和0是否相通:" + marked1);
boolean marked2 = search.marked(7);
System.out.println("顶点7和0是否相通:" + marked2);
}
private boolean[] marked;
private int count;
private Queue<Integer> waitSearch;
public BreadthFirstSearch(Graph G, int s){
marked = new boolean[G.V()];
waitSearch = new Queue<Integer>();
dfs(G,s);
}
private void dfs(Graph G, int v){//使用广度优先搜索找出G图中v顶点的所有相邻顶点
marked [v] = true; //把当前顶点v标识为已搜索
waitSearch.enqueue(v); //让顶点v进入队列,待搜索
while(!waitSearch.isEmpty()){ //通过循环,如果队列不为空,则从队列中弹出一个待搜索的顶点进行搜索
Integer wait = waitSearch.dequeue(); //弹出一个待搜索的顶点
for(Integer w: G.adj(wait)){ //遍历wait顶点的邻接表
if(!marked[w]){ // 该顶点还没被搜索过 对其进行搜索
marked[w] = true; // 将节点放入堆栈中,用于后续的获取该节点的子节点
waitSearch.enqueue(w);
count++; //让相通的顶点+1;
}
}
}
}
public boolean marked(int w)//判断w顶点与s顶点是否相通
{
return marked[w];
}
public int count(){ //获取与顶点s相通的所有顶点的总数
return count;
}
public static class Graph {
private final int V;// 顶点数目
private int E;// 边的数目
private Queue<Integer>[] adj;// 邻接表
public Graph(int V) {
this.V = V; //初始化顶点数量
this.E = 0;//初始化边的数量
this.adj = (Queue<Integer>[]) new Queue[V];// 创建邻接表
for (int i = 0; i < adj.length; i++) {//初始化邻接表中的空队列
adj[i]= new Queue<Integer>() ;
}
}
public int V() {//获取顶点数目
return V;
}
public int E() {//获取边的数目
return E;
}
public void addEdge(int v, int w) {
//把w添加到v的链表中,这样顶点v就多了一个相邻点w
adj[v].enqueue(w);
//把v添加到w的链表中,这样顶点w就多了一个相邻点v
adj[w].enqueue(v);
//边的数目自增1
E++;
}
public Queue<Integer> adj(int v) { //获取和顶点v相邻的所有顶点
return adj[v];
}
}
}
2.4 运行结果
与起点0相同的顶点的数量为:6
顶点5和0是否相通:true
顶点7和0是否相通:false