【决策树】简单介绍+个人理解（二）

news2024/10/2 20:30:21

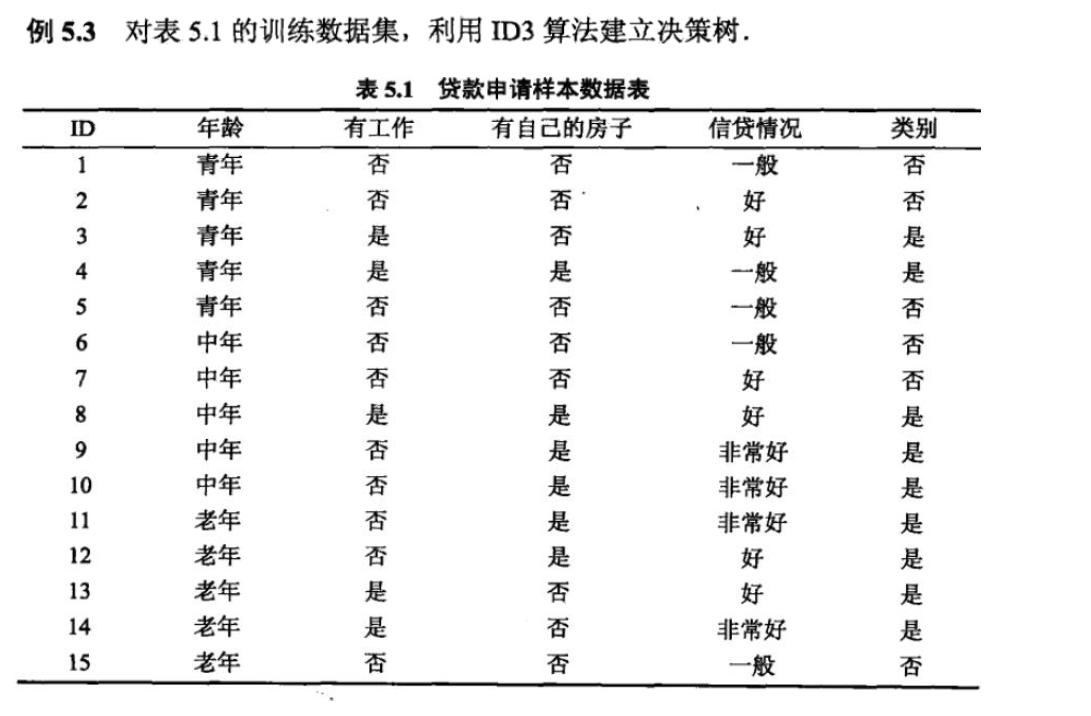
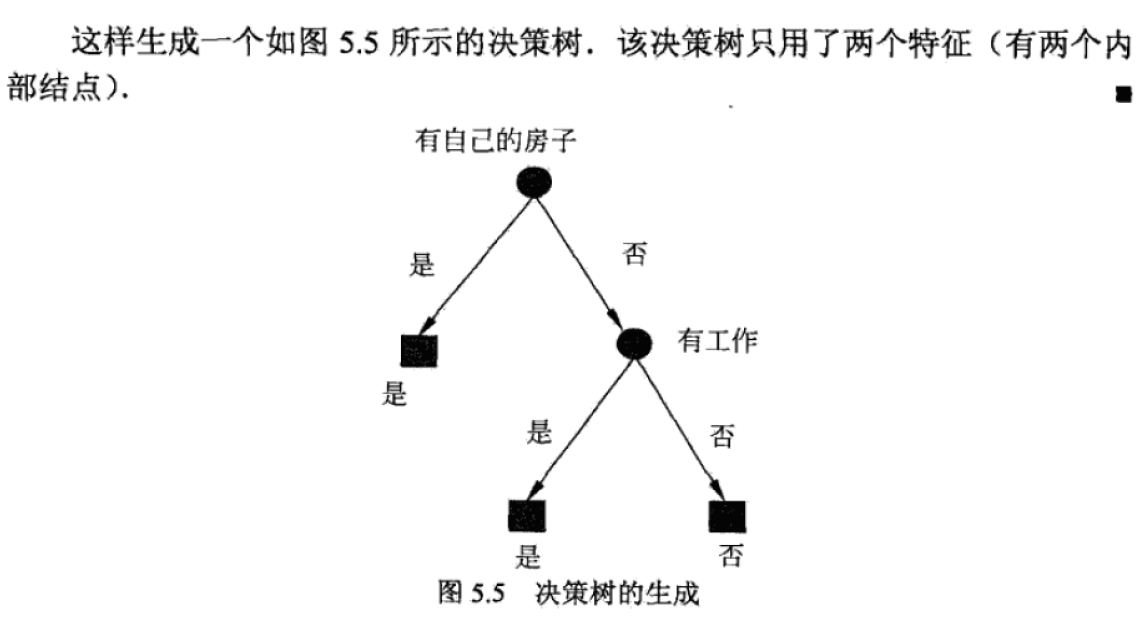
1、ID3(Iterative Dichotomizer)

ID3是Quinlan于1986年提出的, 它的提出开创了决策树算法的先河, 而且是国际上最早的决策树方法, 在该算法中, 引入了信息论中熵的概念, 利用分割前后的熵来计算信息增益, 作为判别能力的度量。
ID3 算法的核心是在决策树各个结点上应用信息增益准则选择特征, 递归地构建决策树. 具体方法是: 从根结点 (root node) 开始, 对结点计算所有可能的特征的信息增益, 选择信息增益最大的特征作为结点的特征, 由该特征的不同取值建立子结点; 再对子结点递归地调用以上方法, 构建决策树; 直到所有特征的信息增益均很小或没有特征可以选择为止. 最后得到一个决策树. ID3 相当于用极大似然法进行概率模型的选择.

ID3算法
输入: 训练数据集 $D$ , 特征集 $A$ , 阈值 $\varepsilon$ ;
输出: 决策树 $T$ .
(1) 若 $D$ 中所有实例属于同一类 $C_k$ , 则 $T$ 为单结点树, 并将类 $C_k$ 作为该结点的类标记, 返回 $T$ ;
(2) 若 $A=\varnothing$ , 则 $T$ 为单结点树, 并将 $D$ 中实例数最大的类 $C_k$ 作为该结点的类标记, 返回 $T$ ;
(3）否则, 计算 $A$ 中各特征对 $D$ 的信息增益, 选择信息增益最大的特征 $A_g$ ;
(4) 如果 $A_g$ 的信息增益小于阈值 $\varepsilon$ , 则置 $T$ 为单结点树, 并将 $D$ 中实例数最大的类 $C_k$ 作为该结点的类标记, 返回 $T$ ;
(5) 否则, 对 $A_g$ 的每一可能值 $a_i$ , 依 $A_g=a_i$ 将 $D$ 分割为若干非空子集 $D_i$ , 将 $D_i$ 中实例数最大的类作为标记, 构建子结点, 由结点及其子结点构成树 $T$ , 返回 $T$ ;
(6) 对第 $i$ 个子结点, 以 $D_i$ 为训练集, 以 $A-\left\{A_g\right\}$ 为特征集, 递归地调用步 (1) ～步 (5), 得到子树 $T_i$ , 返回 $T_i$ .
在这里插入图片描述

2、C4.5

ID3算法使用信息增益（ Info Gain） $\begin{gathered} \operatorname{Info}(D)=-\sum_{i=1}^m p_i \log _2\left(p_i\right) \quad \operatorname{Info}_A(D)=\sum_{j=1}^v \frac{\left|D_j\right|}{|D|} \times \operatorname{Info}\left(D_j\right) \\ \operatorname{Gain}(A)=\operatorname{Info}(D)-\operatorname{Info}_A(D) \end{gathered}$
偏向于具有大量值的属性。在训练集中, 某个属性所取的不同值的个数越多, 那么越有可能拿它来作为分裂属性。
C4.5中使用信息增益率（ Gain ratio） $\begin{gathered} \text { SplitInfo }_A(D)=-\sum_{j=1}^v \frac{\left|D_j\right|}{|D|} \times \log _2\left(\frac{\left|D_j\right|}{|D|}\right) \\ \operatorname{GainRatio}(A)=\frac{\operatorname{Gain}(A)}{\operatorname{SplitInfo}(A)} \end{gathered}$
Info-Gain在面对类别较少的离散数据时效果较好, 之前的 outlook, temperature等数据都是离散数据, 而且每个类别都有一定数量的样本, 这种情况下使用ID3与C4.5的区别并不大。
但如果面对连续的数据（如体重、身高、年龄、距离等）, 或者每列数据没有明显的类别之分 (最极端的例子的该列所有数据都独一无一）, 在这种情况下, ID3算法倾向于把每个数据分成一类（将每一个样本都分到一个节点当中去）, 程序会倾向于选择这种划分, 这样划分效果极差。
为了解决这个问题, 引入了信息增益率 (Gain-ratio) 的概念, 减轻了划分行为本身的影响。
对于取值多的属性, 尤其一些连续型数值 , 比如两条地理数据的距离属性, 这个单独的属性就可以划分所有的样本, 使得所有分支下的样本集合都是 “纯的” (最极端的情况是每个叶子节点只有一个样本)
对于ID (就比如是姓名), 用信息增益划分, 每一个名字都是一个类
所以如果是取值更多的属性, 更容易使得数据更“纯”（尤其是连续型数值）, 其信息增益更大, 决策树会首先挑选这个属性作为树的顶点，结果训练出来的形状是一棵庞大且深度很浅的树, 这样的划分是极为不合理的。
C4. 5使用了信息增益率, 在信息增益的基础上除了一项 split information, 来惩罚值更多的属性
信息增益率引入了分裂信息, 取值数目多的属性分裂信息也会变大, 将增益除以分裂信息, 再加上一些额外操作, 可以有效控制信息增益过大的问题。

3、CART(Classification and Regression Trees)

分类与回归树 (classification and regression tree, CART) 模型由 Breiman 等人在 1984 年提出, 是应用广泛的决策树学习方法. CART 同样由特征选择、树的生成及剪枝组成, 既可以用于分类也可以用于回归. 以下将用于分类与回归的树统称为决策树
CART 假设决策树是二叉树, 内部结点特征的取值为 “是” 和 “否”, 左分支是取值为 “是” 的分支, 右分支是取值为 “否” 的分支
(1) 决策树生成: 基于训练数据集生成决策树, 生成的决策树要尽量大
(2) 决策树剪枝: 用验证数据集对已生成的树进行剪枝并选择最优子树, 这时用损失函数最小作为剪枝的标准

$\clubsuit$ 最小二乘回归树生成算法
输入: 训练数据集 $D$
输出: 回归树 $f (x)$ .

在训练数据集所在的输入空间中, 递归地将每个区域划分为两个子区域并决定每个子区域上的输出值, 构建二叉决策树:

（1）选择最优切分变量 $j$ 与切分点 $s$

$\min _{j, s}\left[\min _{c_1} \sum_{x_i \in R_1(j, s)}\left(y_i-c_1\right)^2+\min _{c_2} \sum_{x_\epsilon \in R_2(j, s)}\left(y_i-c_2\right)^2\right]$
遍历变量 $j$ , 对固定的切分变量 $j$ 扫描切分点 $s$ , 选择使上式达到最小值的对 $(j, s)$ .
（2）用选定的对 $(j, s)$ 划分区域并决定相应的输出值（该区域样本标签平均值）
$\begin{gathered} R_1(j, s)=\left\{x \mid x^{(j)} \leqslant s\right\}, \quad R_2(j, s)=\left\{x \mid x^{(j)}>s\right\} \\ \hat{c}_m=\frac{1}{N_m} \sum_{x_1 \in R_m(j, s)} y_i, \quad x \in R_m, \quad m=1,2 \end{gathered}$
（3）继续对两个子区域调用步骤 (1), (2), 直至满足停止条件
（4）将输入空间划分为 $M$ 个区域 $R_1, R_2, \cdots, R_M$ , 生成决策树
$f(x)=\sum_{m=1}^M \hat{c}_m I\left(x \in R_m\right)$

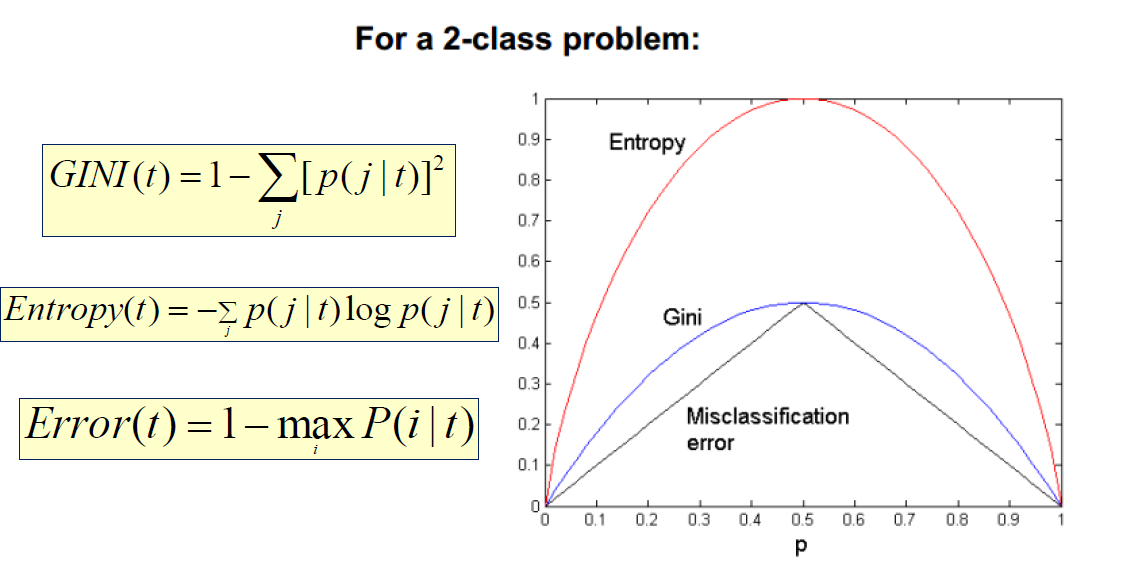
分类树用基尼指数选择最优特征, 同时决定该特征的最优二值切分点

定义 (基尼指数) ：分类问题中, 假设有 $K$ 个类, 样本点属于第 $k$ 类的概率为 $p_k$ , 则概率分布的基尼指数定义为
$\operatorname{Gini}(p)=\sum_{k=1}^K p_k\left(1-p_k\right)=1-\sum_{k=1}^K p_k^2$
对于给定的样本集合 $D$ , 其基尼指数为
$\operatorname{Gini}(D)=1-\sum_{k=1}^K\left(\frac{\left|C_k\right|}{|D|}\right)^2$
这里, $C_k$ 是 $D$ 中属于第 $k$ 类的样本子集, $K$ 是类的个数
如果样本集合 $D$ 根据特征 $A$ 是否取某一可能值 $a$ 被分割成 $D_1$ 和 $D_2$ 两部分, 即
$D_1=\{(x, y) \in D \mid A(x)=a\}, \quad D_2=D-D_1$
则在特征 $A$ 的条件下, 集合 $D$ 的基尼指数定义为
$\operatorname{Gini}(D, A)=\frac{\left|D_1\right|}{|D|} \operatorname{Gini}\left(D_1\right)+\frac{\left|D_2\right|}{|D|} \operatorname{Gini}\left(D_2\right)$
基尼指数 $\operatorname{Gini}(D)$ 表示集合 $D$ 的不确定性, 基尼指数 $\operatorname{Gini}(D, A)$ 表示经 $A = a$ 分割后集合 $D$ 的不确定性. 基尼指数值越大, 样本集合的不确定性也就越大, 这一点与熵相似.